椭球被平面截得的截面面积

黄 之

(上海智启教育培训有限公司 200000)

本文首先得到平面截椭球所得的截面的面积，然后提出一些与此相关的问题.其中一些比较繁杂的运算会省略，因为那将耗费很大篇幅.

一、因为容易看到，任何一个平面截椭球，截面必然是椭圆，其在轴截面的投影也是一个椭圆，所以，应该首先得出平面上椭圆的面积的一般公式.

设xOy面上有一条二次曲线为F:ax2+bxy+cy2+dx+ey+f=0，首先通过平移变换将它的一次项消去.这只需要设F:a(x-s)2+b(x-s)(y-t)+c(y-t)2+g=0,展开后进行系数对比，得到：

众所周知，当判别式Δ=b2-4ac为负数时F为椭圆，为0时F为抛物线，为正数时F为双曲线(都包括退化情形).(s,t)即是F的对称中心，当判别式为0时F所表示的抛物线的中心在无穷远处.

这样，就可以把任何一个椭圆化为形如E:ax2+bxy+cy2+g=0，下面求E的面积.首先将它的xy项消去，即进行旋转变换.易得：将E绕着原点逆时针旋转θ角后的方程为：

(acos2θ-bsinθcosθ+csin2θ)x2+((a-c)sin2θ+bcos2θ)xy+(asin2θ+bsinθcosθ+ccos2θ)y2+g=0

其中A=acos2θ-bsinθcosθ+csin2θ,B=asin2θ+bsinθcosθ+ccos2θ.

(顺便指出，由此可以得到E有两条对称轴：y=k1,2x，其中k为bk2+2(a-c)k-b=0的实根.)

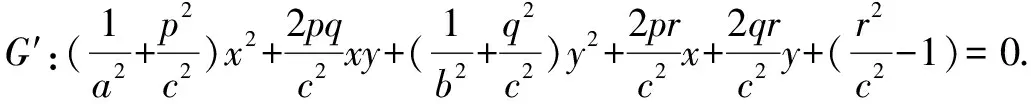
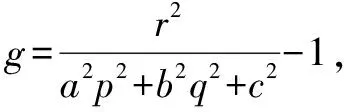
而且可见G与H的位置关系取决于T′=a2p2+b2q2+c2-r2的正负，当T′>0时交于实椭圆，当T′=0时相切，当T′<0时相交于虚椭圆.

那么，由一中的公式可以得到投影G′的面积为：

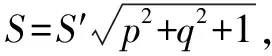
三、现在将平面的方程改为一般式K:Ax+By+Cz+D=0.

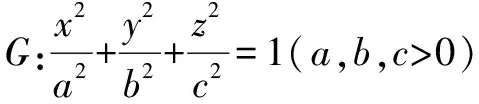
其中T=a2A2+b2B2+c2C2-D2，当T>0时交线为实椭圆，当T=0时平面与椭球相切，当T<0时平面与椭球交于虚椭圆.

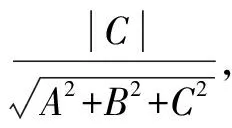
下面将二维的计算结果列出来作对比：

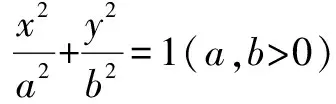
令t=a2A2+b2B2-C2，当t>0时直线与椭圆交于两个不同实交点，当t=0时直线与椭圆相切，当t<0时直线与椭圆交于两个不同的虚交点.

虽然还可以继续计算四维的情形：四维空间中一个三维平面截超椭球所得到的椭球的体积.可是这样的方法显然会使运算量极其庞大！

四、下面来简单的应用一下这个截面面积公式：

1.如果一个平面同时经过椭球

的三个顶点A(a,0,0),B(0,b,0),C(0,0,c),求平面ABC截椭球所得的面积与三角形ABC的面积之比.

2.从椭球外一点P看去，看到的区域面积(观察者认为这平面，不理会视觉差异，定义为这个区域的实际面积)为固定数值S，求所有的P构成的轨迹.

设过P作G的某一个切面的切点为P1(x1,y1,z1)，则该切面的方程为：

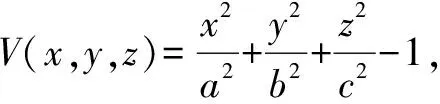
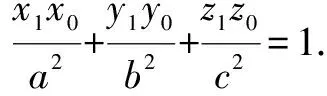
这相当于说，所有的切点都满足下面这个方程：

它是一个平面，故而所有切点都在一个平面上，且切点确定的平面方程就是U.

那么从P(x0,y0,z0)看椭球，看到的就是U截椭球所得到的截面，由文中公式得到：

此问题如果考虑视觉的话，应该会稍微复杂一点，在上述基础上还应乘以某个角的余弦值.

另外，在二维上也可以有类似的问题，比如：

1.从椭圆外一点P看椭圆，总是看到一条长度为定值L的线段，求所有的P构成的轨迹.

2.从椭圆外一点P看椭圆，看到椭圆的视角总是一个给定大小的角(0度至180度)，求P点的轨迹.