巧构辅助量 化繁为简辟蹊径

胡艺雯

(河北省乐亭第一中学 063600)

一、构造辅助角，开辟函数捷径

我们所接触的辅助角是三角函数变换的辅助工具，合理地运用辅助角可以使三角函数取得化二为一的效果，例如可将形如asinx+bcosx的式子化为一个角的三角函数，因此辅助角的引入可以为解决三角函数问题提供捷径.

评注该题目我们运用辅助角对原式进行了化简，其中渗透了数学的整体思想，巧妙地利用诱导公式，使得思路更为简洁.解决本题的方法有很多，我们也可以使用拼凑法逆用两角和差公式求解，也可以使用已知条件进行化切为弦，再用两角和差的正余弦公式求解.

二、巧设辅助数列，开创数列通途

我们在求解数列问题时，如果眼于点仅限于局部则会导致思维量大增，难以获得解题思路，此时我们可以根据问题需要，引入辅助数列，尝试构建一个与原数列有着某种联系的数列，利用辅助数列的桥梁作用，化难为易求解问题.

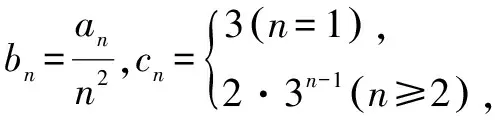
评注我们在证明不等式时，构造了两个辅助数列，并使辅助数列的前n项和等于不等号两边的值，巧妙的将不等式证明问题转换为证明辅助数列前n项和大小关系的问题，构思巧妙，解法简单，在简化思路的基础上取得了高效求解的效果.

三、巧建辅助线，搭建几何便桥

我们通常使用的辅助线对于立体几何问题的求解有着重要的作用，一定程度上可以说辅助线就是立体几何的生命线，因此正确地设置辅助线尤为关键.合理的辅助线可以简明地构造点、线、面之间的位置关系，使得几何结构、性质充分显现出来，后续的作答只需利用线面平行、垂直、相交的定理及性质来求解，这样的解题方式会使思路变得异常清晰，求解更为便捷.

例3 已知α⊥γ，α∥β，求证β⊥γ.

分析求证平面β垂直于平面γ，可在平面γ内构造辅助线b，我们可以运用定理“如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直”，则只需证明b⊂γ且b⊥β.

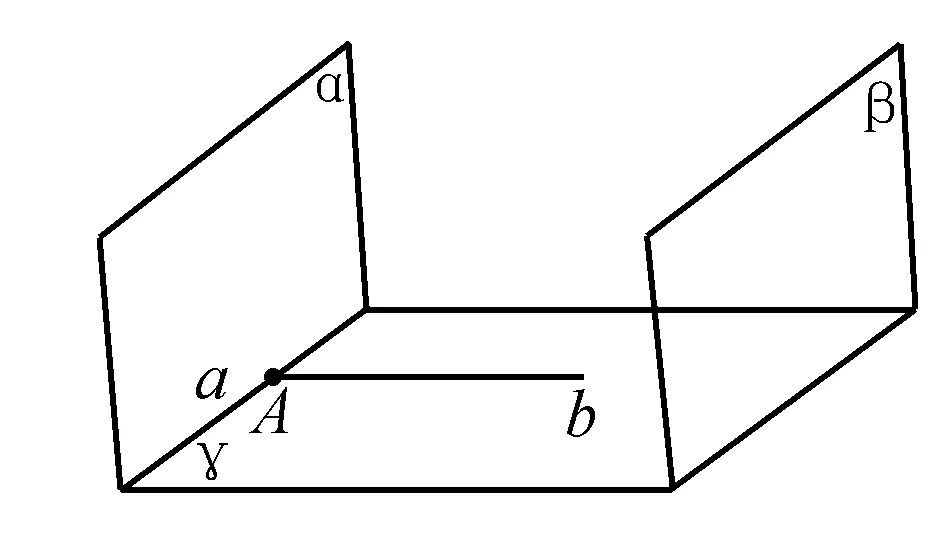
评注求证“两平面垂直”我们运用了平面垂直的判定定理，在一平面内构建了辅助直线，通过证明平面垂直于辅助直线来证明.其中的辅助直线体现了其桥梁作用，使立体几何问题得以转化，从而将原本看似没有关联的元素联系起来，利于分析证明.

综上所述，我们在解题时如若采用构建辅助量的方式，利用辅助量的特殊性使问题变得较为直观，有利于建立原条件与问题之间的数量及空间关系，达到简化问题的目的，方便求解.需要我们注意的是：在学习和使用过程中必须确保辅助量的构造是科学合理的，具有充分的理论依据.