飞行器跨超声速风洞试验模型中尾支撑结构的力学特性研究

□ 郝 东 □ 毛代勇 □ 余 婧 □ 张 林 □ 吴 晗

1.中国空气动力研究与发展中心高速空气动力研究所 四川绵阳 621000

2.中国空气动力研究与发展中心计算空气动力研究所 四川绵阳 621000

飞行器的气动力研究对于飞行器的外形设计、飞行控制等工作具有重要意义，准确的气动力参数可以为飞行器的气动特性设计和飞行控制系统研制提供依据。目前，得到飞行器气动力参数的途径主要有两种，一种是数值仿真［1-4］，另一种是风洞试验［5-7］。 风洞试验无疑是获得飞行器气动力参数最为准确、直接和可靠的手段。大部分飞行器在大型风洞试验时采用的是尾支撑连接方式，设计得到静态刚度高、动态性能好的风洞试验模型尾支撑结构对于飞行器的风洞试验具有现实意义。

笔者针对飞行器2.4 m×2.4 m跨超声速风洞试验，面向风洞全模试验段设计了试验模型的尾支撑结构，并对尾支撑结构进行了力学建模，采用ABAQUS有限元分析求解器求解方程［8］，研究尾支撑结构的静力学和动力学特性，为后续风洞试验支撑结构的研发提供技术支持。

1 力学建模

1.1 结构设计

根据试验模型机械接口尺寸约束、风洞试验段机械接口尺寸约束和气动影响约束等条件，设计了飞行器跨超声速风洞试验模型尾支撑结构，如图1所示。在图 1中，尾支撑结构主要有四部分：模型或天平机械接口、受力杆件、试验段机械接口和信号线走线口。模型或天平机械接口将试验模型或测量天平与尾支撑结构前端相连接。受力杆件是尾支撑结构的主要传力与受力部分。试验段机械接口将尾支撑结构与试验段相连接，将试验模型紧固安装于试验段之中。信号线走线口是测量信号线的走线部分，信号线在尾支撑结构内部走线，可以减小信号对流场的扰动，同时增强信号的稳定性。在图1中，X轴方向为气流方向，Y轴方向在结构对称面内垂直于X轴向上，Z轴、X轴和Y轴形成右手坐标系。

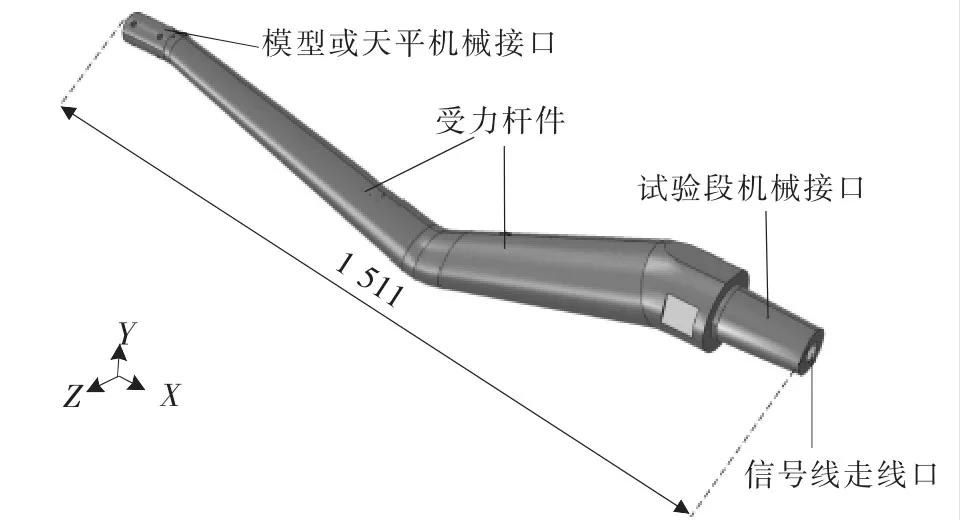
▲图1 尾支撑结构

1.2 等效柔度矩阵

为了得到尾支撑结构三个方向的静态等效柔度特性，在模型机械接口端面施加三个方向的力Fx、Fy和Fz，计算得到对应的位移 ux（Fx）、uy（Fx）、uz（Fx）、ux（Fy）、uy（Fy）、uz（Fy）、ux（Fz）、uy（Fz）、uz（Fz）。

当力为Fx时，尾支撑结构仅在XOY平面内发生变形，则 uz（Fx）=0，即柔度 Jxz=0。 根据 Fx与 ux（Fx）、uy（Fx）的关系，即可得到 Fx对 ux的柔度 Jxx、Fx对 uy的柔度Jxy：

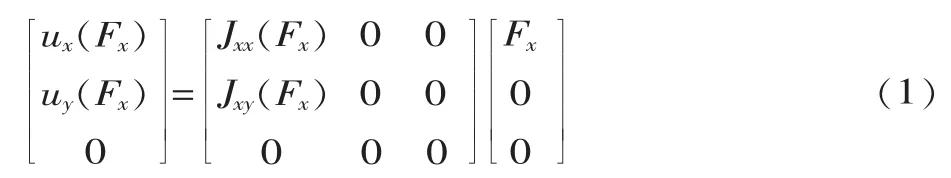
其它两个方向同理。根据力F的作用效果叠加原理，式（1）可以扩展为：

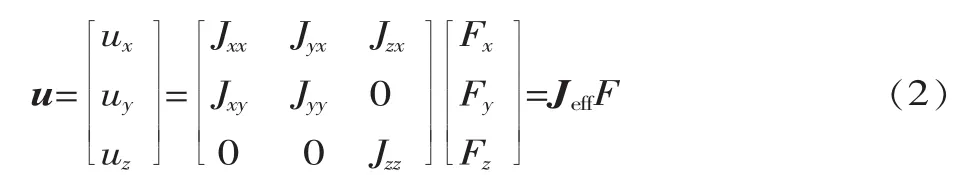
式中：u为尾支撑结构模型安装端的位移矢量；Jyx为Fy对 ux的柔度；Jzx为 Fz对 ux的柔度；Jyy为 Fy对 uy的柔度；Jzz为Fz对uz的柔度；Jeff为等效柔度矩阵。

则等效刚度矩阵Keff为：

经过大量仿真发现，在考虑几何变形影响时，尾支撑结构模型安装端某一方向的位移ui与该方向的力Fi具有如下数学形式：

式中：a和b均为待确定系数。

1.3 有限元求解

采用四节点四面体单元进行网格划分，单元长度设为10 mm，试验段机械接口为固定支撑边界条件，加载位置为模型或天平机械接口的端面。尾支撑结构的制造材料为00Ni18Co8Mo5TiAl马氏体时效钢，简称F141［9］，其弹性模量为 187.25 GPa，泊松比为 0.274 3，密度为8 000 kg/m3。尾支撑结构总质量为102 kg。所得到的有限元模型如图 2所示，单元数为109 870，节点数为22 623，总自由度数为67 869。将有限元计算结果用于检验等效柔度矩阵模型，并分析尾支撑结构的动态特性。

▲图2 尾支撑结构有限元模型

2 仿真分析

2.1 静态特性

将有限元计算结果作为准确值，用于确定等效柔度矩阵中的各个元素。在有限元计算中，力Fx、Fy、Fz的取值为 20 000 N、40 000 N、…、200 000 N。

当作用力在X轴方向时，ux、uy与Fx的关系曲线如图3所示。当作用力在Y轴方向时，ux、uy与Fy的关系曲线如图4所示。当作用力在Z轴方向时，ux、uz与Fz的关系曲线如图5所示。拟合得到的等效柔度矩阵元素结果见表1。

表1 等效柔度矩阵元素

由图3～图5和表 1结果可知，所建立的等效柔度矩阵模型能够很好地表征尾支撑结构的总体柔度特性，等效柔度矩阵计算值与有限元直接仿真值具有较好的一致性，三个方向的拟合度均在0.999 99以上。此外，通过研究还发现，等效柔度矩阵中的每个元素值并不是一个常数，而是与关联方向的力成二次关系，且常数项为0。

为进一步验证所建立的尾支撑结构等效柔度矩阵的正 确性 ，选择 载 荷 （Fx、Fy、Fz）为 （30 kN，25 kN，25 kN）、（30 kN，40 kN，25 kN）、（30 kN，40 kN，45 kN）、（50 kN，40 kN，25 kN）、（50 kN，40 kN，45 kN） 共五种复合加载情况进行验证，有限元计算结果与等效柔度矩阵计算结果见表2。由表2可知，在复合载荷情况下，最大相对误差小于5%，满足工程上快速估算的使用要求。

2.2 动态特性

在分析尾支撑结构的静态特性之后，对其动态特性进行研究。

为了得到尾支撑结构的动力学特性，首先采用兰乔斯法对其进行模态分析，模态分析是结构动态分析中的一种有效分析方法［10-11］。兰乔斯法是一种将对称矩阵通过正交相似变换为三对角矩阵的算法，广泛应用于结构动力学方程的求解中。

计算得到的模态频率范围为74.163～930.82 Hz，前 八 阶 的 模 态 频 率 为 74.163 Hz、76.251 Hz、239.95 Hz、240.62 Hz、576.65 Hz、580.74 Hz、879.25 Hz、930.82 Hz，前两阶模态振型为绕Y轴一阶弯曲，如图6所示。

▲图3 Fx与 ux、uy关系曲线

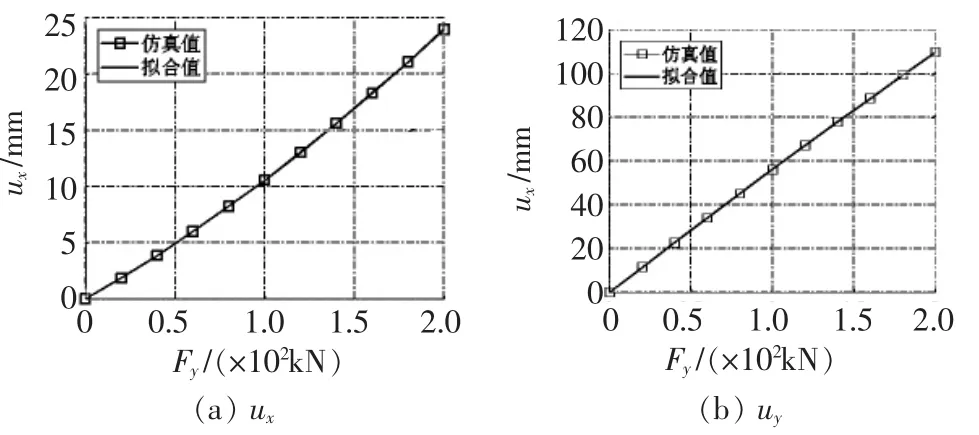
▲图4 Fy与 ux、uy关系曲线

▲图5 Fz与 ux、uz关系曲线

▲图6 前两阶模态振型

由模态分析可知，所设计的尾支撑结构的前两阶模态频率（74.163 Hz和76.251 Hz）远大于其它支撑结构的前一阶模态频率（31.1 Hz），三阶模态频率（239.95 Hz）大于其它支撑结构的二阶模态频率（120.9 Hz）［12］。

在分析了尾支撑结构的模态后，对其受冲击响应进行分析。

冲击载荷是进行风洞试验时最为恶劣的一种载荷，对冲击载荷衰减的快慢反映了支杆快速稳定能力的强弱。瑞利阻尼因数α=0.2、β=0.000 9，当三个方向分别受到幅值为20 000 N、脉宽为0.01 s的冲击载荷时，尾支撑结构模型安装端的位移时间响应曲线如图7所示。

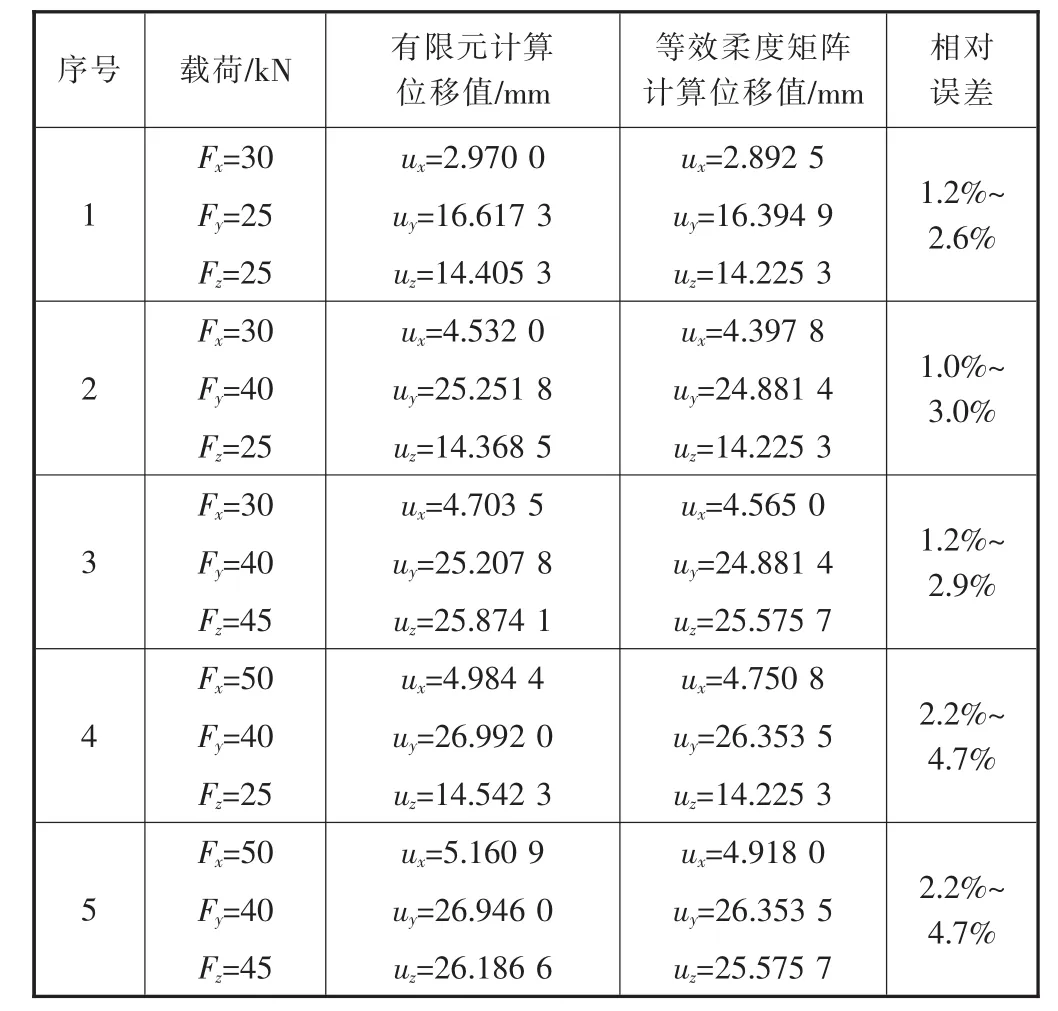
表2 复合载荷验证结果

由图7可知，X轴方向的位移响应远远小于Y轴和Z轴方向的位移响应，且X轴方向恢复稳定的时间远远短于其它两个方向，即X轴方向的刚度和阻尼比Y轴和Z轴方向的大。在0.02 s之后，三个方向的位移均衰减到5 mm以内，满足风洞试验的要求，可见尾支撑结构能够给风洞试验模型提供一个较为稳定的试验支撑平台。

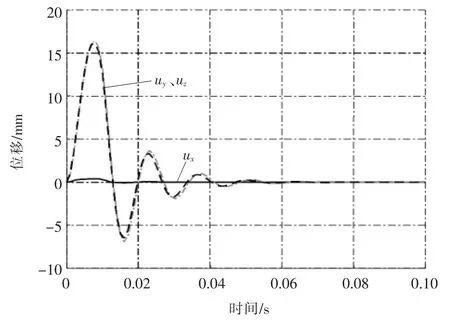
▲图7 冲击载荷时位移时间响应曲线

3 结论

笔者针对2.4 m×2.4 m跨超声速风洞试验，设计了飞行器跨超声速风洞试验模型的尾支撑结构，得到了尾支撑结构的等效柔度矩阵，分析了尾支撑结构的静力学和动力学特性。

分析结果表明，所设计的尾支撑结构具有较高的静态刚度和良好的动力学稳定性，满足风洞试验的结构要求。所建立的等效柔度矩阵能较好地描述尾支撑结构的总体柔度特性，等效柔度矩阵计算结果与有限元计算结果最大相对误差在5%以内，满足工程应用的要求。在20 000 N冲击载荷作用下，三个方向的位移稳定到5 mm以内的时间均短于0.02 s，尾支撑结构能够给风洞试验模型提供一个较为稳定的试验支撑平台。