基于光场三维重构和PSP的曲面压力测量技术

李浩天, 许晟明, 赵 洲, 张翰墨, 施圣贤,*

(1. 上海交通大学 机械与动力工程学院, 上海 200240; 2. 上海航天控制技术研究所, 上海 201109)

0 引 言

自20世纪80年代开始，压敏漆测压技术作为一种基于高分子聚合物光致发光和氧猝灭效应的非接触式测量技术广泛应用于空气动力学领域，该技术与传统离散点压力测量技术相比，其压力测量分辨率仅受限于图像采集系统，因而具有测量精度高、不受复杂模型结构影响等优点。近年来，PSP测量技术在国内获得了快速发展和广泛应用，中国空气动力研究与发展中心、中国航天空气动力技术研究院、中国航空工业空气动力研究院、西北工业大学和上海交通大学等众多科研单位及高校对PSP测量技术开展了深入研究。不仅进行了大量稳态流场PSP测量试验，对快速响应PSP动态测量技术展开了研究，还完善了二维PSP测量系统及图像处理算法，并对压力分布和温度场的同步测量进行了相关研究。除此之外，国内对三维PSP测量技术也开始展开了相应研究，其中西北工业大学高丽敏通过在涂有压敏漆的叶片表面上标注多个特征点的方法，成功测量了叶片表面的三维压力分布，并完善了相关算法[11]。

目前，国际上三维PSP测量技术均基于多相机系统。德国DLR率先使用基于8个相机的三维PSP测量系统，完整地测量了M346教练机各个部分的三维表面压力分布[14]。英国ARA使用基于12个相机的PSP系统测量了超声速风洞中萨伯“鹰狮”飞机的三维表面压力分布[15]。但是基于多相机的三维PSP测量系统不但提高了实验难度、增加了硬件成本，更为重要的是极大限制了在受限光学空间下的应用。因此，倘若能用单台相机实现三维模型表面压力分布测量，将极大简化实验难度，推进空气动力学的进一步发展。近年来，光场三维成像技术的快速发展为单相机三维PSP技术提供了一种全新的方案。光场“Light Field”概念由Arun Gershun于1936年首次提出，是指空间传播光线的集合。斯坦福大学Ng Ren博士于2005年开发出世界首台紧凑型光场相机，并随之推出了Lytro品牌的光场相机[16]，加速了光场技术的应用。在科学实验测量领域，上海交通大学施圣贤及美国Brain Thurow将光场成像与粒子图像测速技术(Particle Image Velocimetry, PIV)相结合，提出了三维光场粒子测速技术(Light-Field Particle Image Velocimetry，LF-PIV)，并成功应用于流体力学实验研究中[17-25]。借鉴光场成像技术在实验流动测试技术的成功应用经验，本文提出了一种基于单光场相机和压敏漆的三维表面压力分布和模型三维结构尺寸同步测量技术(LF-3DPSP)。

1 光场三维PSP技术

LF-3DPSP基于传统光强法PSP技术发展而来，主要包括2个独立的部分：(1) 基于光场的PSP测量；(2) 三维模型的光场重建。该技术与传统PSP技术相比，具有相似的实验步骤，但Wind-on和Wind-off图像均由光场相机采集。此外，为了重构模型三维结构尺寸，需要额外拍摄带投影纹理模型的光场图像。本节将详细介绍如何通过光场渲染和光场重建算法处理获得三维模型表面的压力分布，图1列出了LF-3DPSP的关键图像处理步骤，包含了该技术所使用的校准环节，压力测量和模型尺寸测量环节，以及相关步骤所使用的算法。

1.1 基于光场的PSP测量

压敏漆受到一定波长的光源照射后，涂层中的探针分子进入电子激发态，并通过发射波长更长的光来耗散吸收的能量；同时，激发态探针分子与氧分子碰撞，转移吸收的能量，最终回到基态。上述过程被称为Stern-Volmer过程，通常使用一阶线性的Stern-Volmer方程表示[3]：

(1)

上式中：I指压敏漆的发光强度；B(T)、A(T)为与温度有关的Stern-Volmer常数；p表示压敏漆表面压力；下标ref表示参考状态。

图1 LF-3DPSP算法流程示意图，其中柱状框表示处理环节，方框表示环节内具体的步骤，虚线框表示步骤所属算法

Fig.1FlowchartoftheimageprocessingstepsfortheLF-3DPSPtechnique,columnarboxmeansprocesspart,squareboxmeansprocessdetailedstepanddottedlinedboxmeansthealgorithm

在PSP技术中，吹风前拍摄的Wind-off图像和开启风洞后拍摄的Wind-on图像分别表示上式中Iref和I，根据光强法可以计算得到风洞中压敏漆表面压力分布。由于LF-3DPSP技术使用光场相机记录Wind-on和Wind-off条件下压敏漆的发光强度，而光场图像和一般图像有着明显不同的性质，一般图像由单个像素点组成成像基本单元，而图2中的光场图像则由与微透镜同样形状的像素团组成成像基本单元，这也是光场图像能记录光线多维信息的本质原因，因此需要对Wind-on和Wind-off原始光场图片进行如图1中所示的压力测量部分的预处理工作。通过光场渲染算法(Light-Field Render algorithm)处理生成多个视角图像，该多视角图像包括了一般相机正视图像(中心视角)和周围多个视角，详见下文。从多视角图像中分别取出对应的Wind-on和Wind-off中心视角图像，即为用于压力计算的PSP图像。最后，通过式(1)计算得到中心视角对应的模型压力分布。该技术中除中心视角外，其余视角均可用于计算压力分布，但是其余视角计算的模型压力分布与后续计算的模型尺寸深度图并非同一视角(深度图为中心视角图像)，因此需要校正至同一视角，从而引入额外误差。所以本文仅使用中心视角图像计算模型压力分布。

图2 (a) Wind-on光场图像与红色方框区域放大图; (b) Wind-off光场图像与红色方框区域放大图；(c) 带投影纹理的截锥体模型光场图像

Fig.2Examplesof(a)wind-onexcitationlight-fieldimageanditszoom-indetail, (b)wind-offexcitationimageanditszoom-indetailand(c)dottedlight-fieldimageanditszoom-indetailforthetruncatedconemodel

在进行光场渲染之前，需要先确定光场相机微透镜中心坐标，即进行微透镜校准(MLA calibration)，该校准过程在拍摄前后均可进行，无需移除模型。首先，调节光场相机的光圈至最小后拍摄白色平面，获得由白点矩阵和黑色背景构成的微透镜校准光场图像[16]。最后，使用高斯拟合处理得到具有亚像素精度的微透镜中心坐标，从而建立每个微透镜和像素点的对应关系。完成微透镜校准后，使用校准结果进行光场渲染处理生成多视角图像。通过取出每个微透镜下对应的像素团中特定位置的像素，并按微透镜的排列顺序进行组合，最后形成一张子视角图像。该子视角方位与像素团中提取像素的位置有关，其中每个像素团的中心像素组合形成中心视角图像，而提取像素团中不同位置的像素会组合形成不同视角的图像，即本文所述的多视角图像[16]。如图3(a)简化的一维光场成像原理所示，红色像素代表每个微透镜下方像素团中心像素，蓝色像素代表每个像素团中最下方像素。图3(b)表示将像素传感器扩展至二维平面，由于微透镜均为圆形结构，灰色区域则表示微透镜下的像素团。将每一个像素团的中心像素(红色像素)提取并排列拼合后构成了图3(c)的中心视角图像，由于视角方向与像素位置相反，蓝色像素则构成了最上方的子视角图像，绿色像素则构成了最右边的子视角图像。

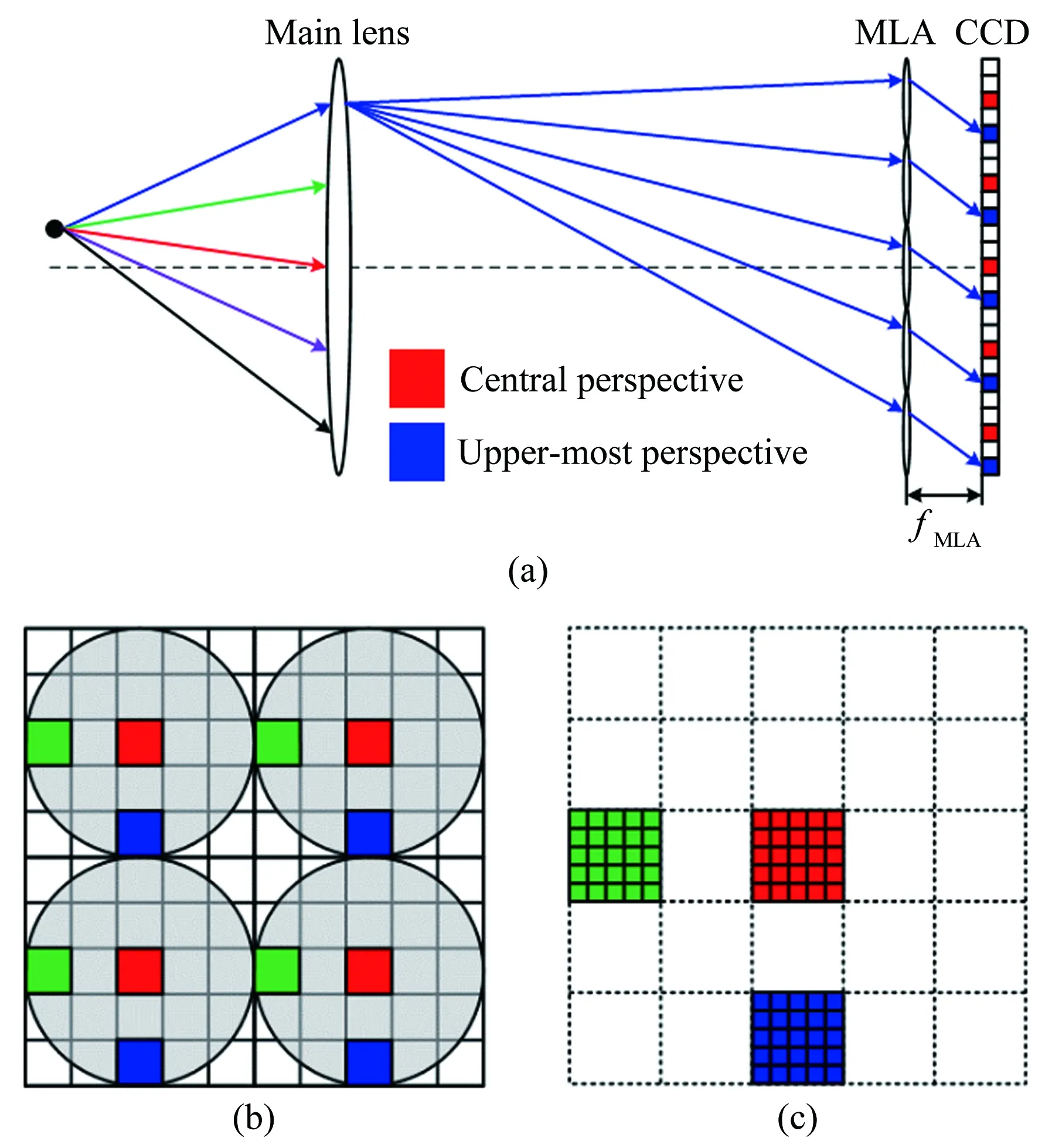
图3 (a) 一维光场示意图；(b) 微透镜下CCD图像；(c) 红色、蓝色像素和绿色集合分别表示形成的中心视角图像、中心最上方视角图像和中心最右边视角图像

Fig.3Principleofthelightfieldperspectiveshiftalgorithm(a)1Dschematicofthelight-fieldcamera, (b)sub-imageoflenslet(showingonlyfourlensletshere)and(c)artificiallygeneratednewperspectiveimages(showingonlythecentral,upper-mostperspectivesandright-mostperspectives)

1.2 三维模型的光场重构

基于PSP测量技术的基本原理，模型表面需进行压敏漆喷涂处理，因此表面较为光滑且无纹理，难以使用现有光场三维深度算法对这种表面模型进行精确地深度计算。为准确测量模型三维结构尺寸，本文使用投影仪向模型投影图像，从而增加模型的纹理，其目的是区别模型不同区域以增加深度计算的精度。投影纹理具有多种选择，该技术采用如图4所示的密集白底黑点图案。此外，因为投影纹理只是为了增加模型纹理，投影纹理变化并不会对重构结果产生影响。带纹理模型的光场图像拍摄过程在Wind-off和Wind-on条件下均可进行，并且无需对模型和光场相机进行任何移动。作为验证性试验，本文仅在Wind-off条件下进行带纹理模型的光场图像拍摄，并且使用基于北京航空航天大学的光场深度算法[26]和KAIST的光场后处理算法[27]对带纹理模型的光场图像进行深度计算。

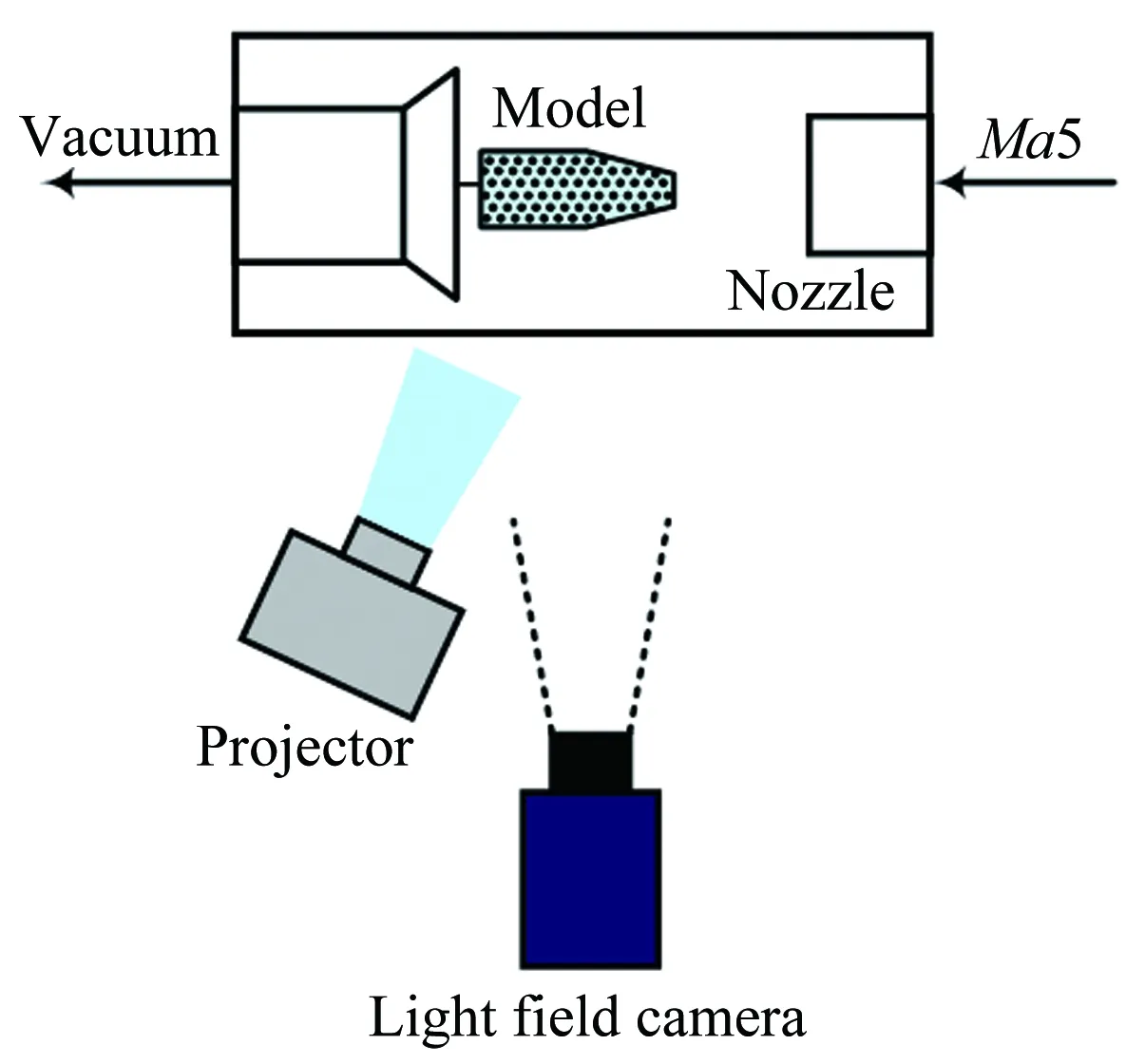
图4 光场相机拍摄带投影纹理三维模型图像

光场相机形成多视角图片有一定的规律性，因此可以形成图5(b)中以中心视角(正常视角)为核心的方形矩阵分布的多个视角。如图5(a)所示，u-v平面表示视角平面，s-t平面表示相机图像平面，被拍摄物体上的某一点P在不同视角图像中具有不同的像素坐标，即相对于中心视角的P(s0,t0)有一定程度的偏移，而偏移大小和该点与相机的距离有关。若在多视角图像中选取中心一行视角图像，则P点在该行视角的像素坐标沿水平方向进行偏移P(s0,t0)→P(si,t0)，且相邻图像的偏移量相同。同理，在中心列视角中P点像素坐标沿垂直方向进行了偏移P(s0,t0)→P(s0,ti)。为更好地描述像素偏移产生的视差，本文使用外极线图像(Epipolar Plane Image, EPI)进行计算。如图5(a)所示，当固定t和v时，空间中点P的光线(绿色)将投影到切片平面s-u上；同理，固定s和u时，蓝色光线投影至切片平面t-v上，最终形成EPI。如图5(b)所示，将同一行视角图像(固定t)的同一行像素(固定v)组合形成如图5(c)所示的EPI图像，其中每条极线的斜率大小表示了该点在各视角中像素的偏移程度，最后形成视差图(Disparity map)，得到对应的深度信息。其中深度信息和EPI斜率的关系由式(2)确定

Δu=-(f/Z)Δs(2)

上式中：Z表示空间中点沿相机轴线方向的距离；Δu和Δs分别表示P点光线在相机坐标和图像坐标中的变化；f表示焦距。

由于每个子视角图像均有对应的视差图，通常以中心视角对应的视差图为计算结果。首先，通过光场渲染得到多视角图像，分别取出多视角图像中心行和中心列进行组合形成2组EPI。使用具有较高鲁棒性的旋转平行四边形边缘算子(Spinning Parallelogram Operator, SPO)对2组EPI进行极线的边缘检测[26]。该算子在极线斜率变化范围内均匀离散化得到N个斜率值，按顺序标注标签(1～N)，并对每个斜率计算得到2组三维初始深度矩阵(Cost volume)。该三维矩阵的维度分别表示图像的横纵轴以及标签，矩阵值表示可信度大小，标签值代表一系列离散的斜率信息(深度信息)，可信度越大表示该点所在标签代表的深度越接近正确值。

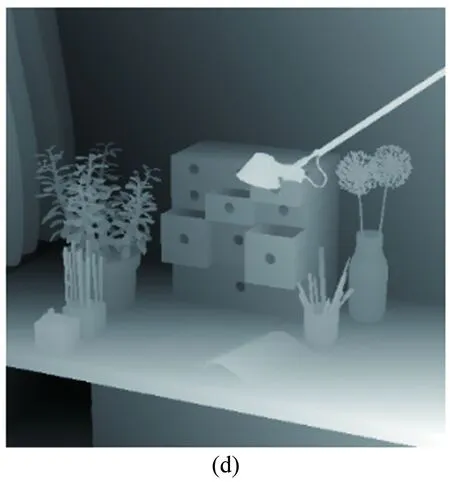
图5 (a) EPI原理; (b) 3×3视角图像，红线表示同行像素；(c) 图(b)中红线代表的EPI；(d) 由EPI生成的视差图

Fig.5(a)TheprincipleofEPI, (b)horizontallineperspectivesandsamelinepixel, (c)EPIfromtheredlineinFigure(b), (d)disparitymap

然后，使用引导滤波器对三维矩阵的每一标签层进行保边平滑处理，消除误差。再通过Winner-take-all策略，取出三维矩阵中沿标签维度方向最大值所对应的标签，得到由视差标签组成的二维矩阵，该矩阵即为初始视差图。最后，对初始视差图进行后处理得到最终真实深度结果，后处理包括加权中值滤波，光场相机尺度校准和椭圆拟合再优化过程。为了获取准确的三维尺度，需要进行光场尺度标定，将视差值转为真实深度值。光场尺度校准与光场微透镜校准类似，只需固定镜头焦距不变，在试验前后均可进行。光场相机尺度校准设备包括校准板，电动位移台和光场相机等。校准过程中，电动位移台沿相机轴线方向多次移动校准板，光场相机固定不动并拍摄得到一系列如图6所示的不同距离的校准板光场图像，并计算初始视差图。由于连续2张视差图的真实位移距离已知，通过拟合可得视差值和真实深度值的函数关系。因此，基于校准结果，视差图可转换为真实深度图(Depth map)。此外，上述过程中深度值或视差值均为整数精度的离散点，所以需要对深度结果进行连续性拟合。椭圆拟合再优化过程是基于已知截锥体模型表面本身的曲率特性，将深度值沿模型圆周方向进行椭圆方程拟合，连续化深度信息并降低由于投影光斑过于稀疏造成的计算误差，最终得到具有连续深度分布的三维模型。

图6 局部放大后校准板的原始光场图像

2 验证性风洞试验

2.1 试验条件与模型

为验证LF-3DPSP技术的可行性，在英国曼彻斯特大学的高超声速风洞中进行了验证性试验。风洞自由来流马赫数为5，总压p0=810kPa，静压pinf=1.6kPa，风洞运行时间t=7.5s，温度保持300K不变。

LF-3DPSP测量系统主体架构与一般二维PSP测量系统设备类似，除采用光场相机替代普通相机并增加投影纹理模型的拍摄过程外，其余均采用Erdem论文中[28-31]相同的设备和模型。该试验中使用的压敏漆的组成成分和校准过程见文献[32]。试验模型采用具有大范围曲率变化和压力变化的截锥体模型，易于验证该技术的正确性。

2.2 试验结果与分析

Wind-on和Wind-off光场图像与带投影纹理模型的光场图像均由作者自主开发的光场相机进行拍摄。该光场相机基于分辨率为6600pixel×4400pixel的 Imperx B6640相机搭建，采用尼康200mm微距镜头，并使用610nm波段的光学滤片进行滤光。基于相关分析[20]，将分辨率为408pixel×314pixel的微透镜阵列放置于主镜头和传感器之间的焦平面上构成光场相机。

试验时，拍摄完毕后使用图1所示的步骤对原始光场图像进行处理。首先，进行光场微透镜校准和尺度校准；然后，原始光场图片经过光场渲染生成分辨率为800pixel×523pixel、数量为5×5的多视角图片；使用Wind-on和Wind-off条件下的中心视角图片计算压力分布(与传统二维光强法PSP计算过程相同)；并且基于光场相机尺度校准的结果，对带投影纹理模型的多视角图片进行深度计算,得到如图7(a)所示的模型表面深度图；最后，将模型深度图片和压力分布图片进行融合，最终形成三维压力分布图。该压力分布结果为连续10张Wind-on光场中心图像进行均值化处理后计算得到，且未进行任何后处理。

图7 (a) 模型深度尺寸; (b) 计算结果与理论模型在模型中轴线上(y=35mm)的绝对误差分布

Fig.7(a)Estimated3Dgeometryand(b)3Destimationabsoluteerroralongthecentralline(y=35mm)

由于该截锥体模型由CNC加工，具有极高的表面精度，误差为±20μm，因此三维结构尺寸计算误差以模型设计尺寸作为参考。图7(b)表示该计算结果在x=10～74mm的范围内绝对误差均小于1mm，整体最大误差在2mm左右，证明该技术可以有效进行大曲率模型的三维结构尺寸测量。但是由于投影斑点不够密集，造成部分区域缺少纹理，对计算结果造成了一定影响。

模型压力分布如图8(a)所示，L表示模型长度，R表示该截锥体最小截面半径。在吹风阶段，模型有轻微的旋转，头部向下旋转约1.5°。空气经过如图8(c)中所示的弓形激波后，在迎风向的锥形面处被激波压缩，导致该处压力增大，造成了图8(a)中压力分布不均匀，且最大压力出现在迎风向的锥形面上。在模型截锥体和圆柱体交界处产生膨胀波，形成一个扇形连续膨胀区，因此圆柱形部分上的压力相对较低。图8(b)中模型轴线上压力分布清楚地表明了上述压力变化，图8(c)纹理图像则清晰地显示了模型弓形激波和膨胀波的位置，该纹理图像和Erdem论文[29]中图4.25的截锥体模型CFD马赫数云图结果一致。而且在相似的工况条件下，风洞中截锥体偏移一定角度的压力分布在Yang论文[31]中已有详细论述，本试验截锥体偏移角度较小，在模型迎风向锥形面处形成符合Yang论文[31]中描述的“漏斗”状压力分布，且整体分布趋势和该论文中的结果相同。由于本试验工况与Erdem论文[29]和Yang论文[31]试验工况有所不同，本文只进行简单的定性分析，后续将开展一系列定量分析。

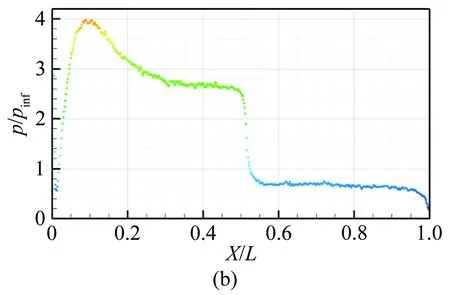
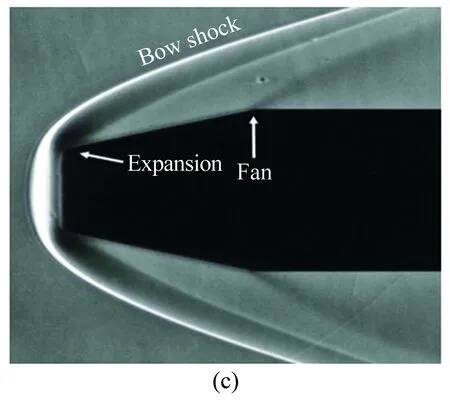
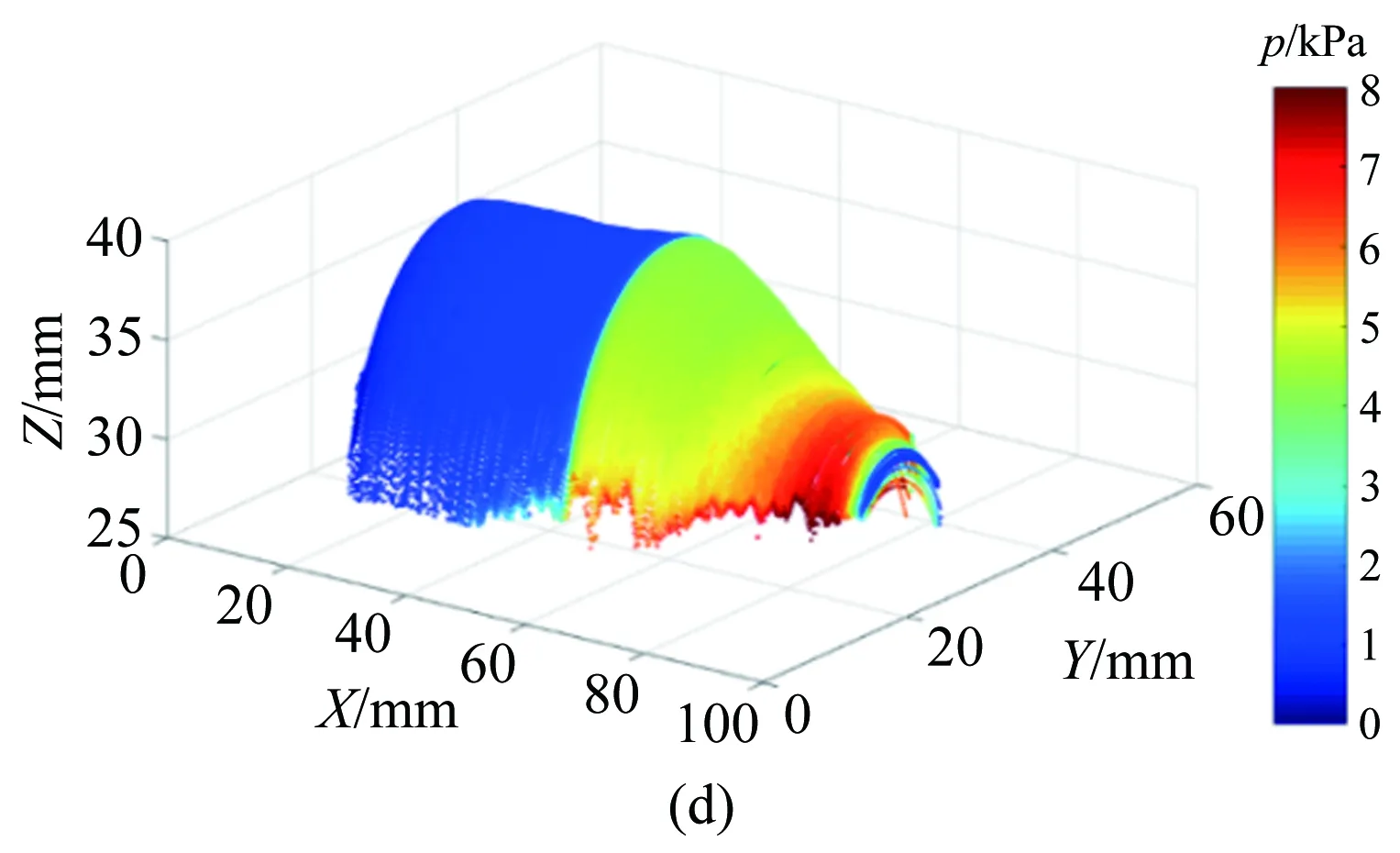
图8 (a) 模型二维压力分布图；(b) 模型轴线上相对压力分布；(c) 模型纹影图像；(d) 模型三维压力分布

Fig.8(a)Measured3Dsurfacepressuredistributionforthemodel, (b)pressuredistributionalongthecentralplane, (c)Schlierenimageand(d)Measured3Dsurfacepressuredistributionforthemodel

3 结 论

提出了一种全新的基于单光场相机和压敏漆的三维表面压力测量技术——LF-3DPSP，并以截锥体为例，在马赫数为5的高超声速风洞中对该技术进行了验证性试验研究。

(1) 相较于多相机系统，该技术仅采用单台相机、单个视角进行三维表面的压力测量，试验设备和处理方法更为简单，并且特别适用于光学空间受限情况下的复杂三维表面压力测量;

(2) 在试验中获得了精度较高的大曲率三维连续表面模型尺寸，并且获得了与纹影结果相匹配的三维连续表面压力分布结果。

该技术采用的密集白底黑点纹理较为稀疏、简易，后续将考虑使用更为细致复杂的投影纹理增加精度。并且在模型尺寸重构的过程中，可同时采用Wind-off和Wind-on条件下的带纹理模型的光场图像进行模型深度计算，经过校正后可进一步提高模型三维尺寸测量精度。