阴影难题巧解

题目：求图1中阴影部分的面积。（单位：厘米）

图1

解法一：把图1平均分成四个小正方形（如图2所示），先求出一个小正方形阴影部分的面积，即用小正方形的面积减去两个空白部分的面积，小正方形的面积是5×5＝25（平方厘米），其中一个空白部分的面积是25－3.14×5×5÷4＝5.375（平方厘米），小正方形阴影部分的面积是25－5.375×2＝14.25（平方厘米）。整个图形阴影部分的面积是14.25×4＝57（平方厘米）。

所以，阴影部分的面积是57平方厘米。

图2

解法二：把图中8个扇形的面积加在一起，正好多算了一个正方形的面积，而8个扇形的面积又正好等于两个整圆的面积。

（10÷2）2×3.14×2－10×10＝157－100＝57（平方厘米）

答：阴影部分的面积是57平方厘米。

同学们，你学会了吗？请你解答下面这道题。

有一块正方形草坪，边长为10米（如图3），在对角线两端上各打一根木桩，桩上各拴一头牛，绳长10米。两头牛都能吃到的草地的面积是多少平方米？

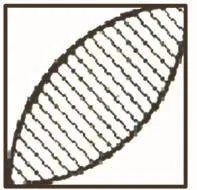
图3