一道均质链绳问题的多样化思路教学

陈 辉

(永康市第一中学,浙江 金华 321300)

在物理中有一类细线和轻绳,材质柔软质量不能忽略,均匀分布,这样的模型叫均质链绳.与链绳有关的静力学、动力学问题是高中物理竞赛重点考察内容之一,题设非常简洁,又能很好地考察学生运用数学解决物理问题的综合能力,链绳问题与高考题型截然不同,用常规解题思路难以入手.在重视物理核心素养的教学背景下,中学物理教学应有意识地多角度分析问题,归纳比较形成一套思想方法体系,培养学生学习兴趣,调动学习积极性,思维灵活性、创造性.[1]本文通过一道经典均质链绳竞赛题的多样化思路教学探索培养学生优秀思维品质的教学途径.

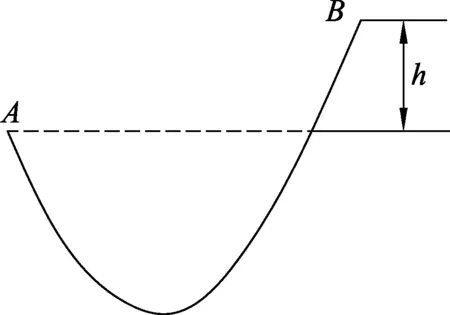
图1 均质链绳

均匀不可伸长的绳子如图1,两端悬挂在A、B两点,B比A高h.在A点绳子张力为TA,绳子的质量为m,绳长为l.

(1) 求B点绳子的张力;

(2) 假设有一根与AB绳一样形状的光滑弯曲管道,绳恰好铺在整根管道中,A、B两端用手拉住,求放手瞬间绳子的加速度大小.

1 静力学分析

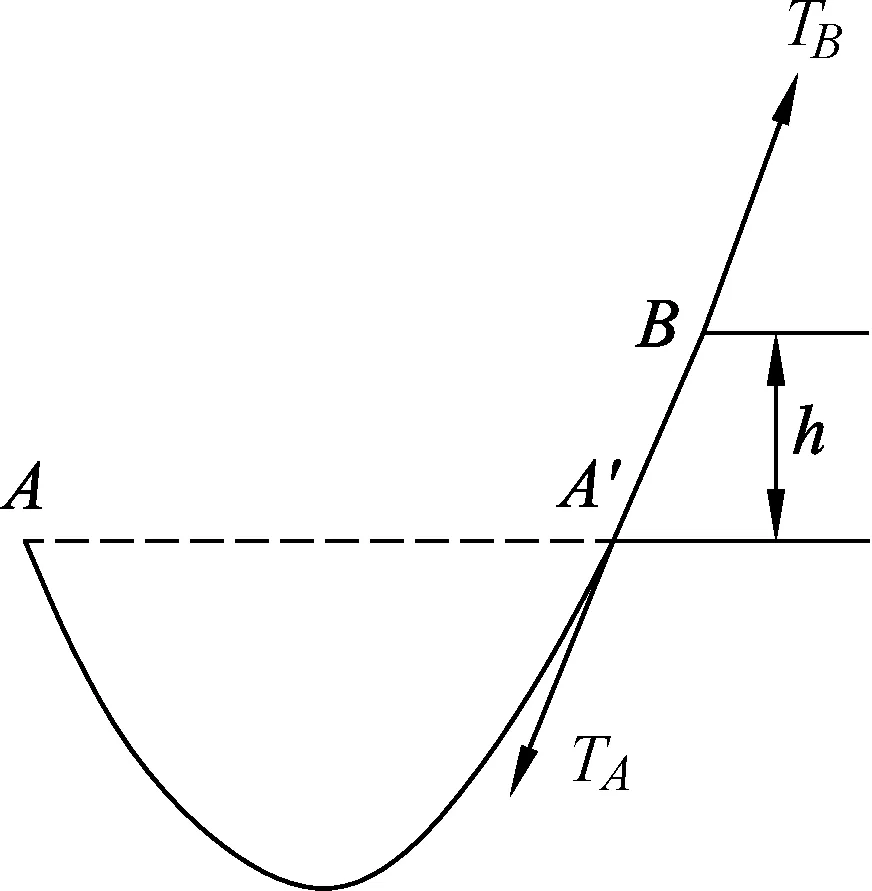
图2 等效建模

求B点绳子张力是一个静力学问题,可分别运用微元积累、补偿法、虚功原理3种思想方法.

1.1 微元积累

图3 受力分析

每段绳子沿x正方向的拉力比负方向的拉力大ΔT,因为α→0、β→0,Ti+1cosα≈Ti+1,Ticosβ≈Ti,所以ΔT=Ti+1-Ti=Δmgsinθi,两边累加可得

B、A′张力差值为∑ΔT=TB-TA′,∑Δxsinθi是该段绳Δx在竖直方向上的投影，∑Δxsinθi=∑Δhi=h,整理得

图4 等效建模

1.2 补偿法

补偿法指对原模型进行填补,然后对填补部分进行分析,以达简化问题的方法.

用长为L的光滑斜面放在A、B两点,加段直绳沿着斜面将原来绳子接通,如图4.原链绳与直绳整体处于平衡状态,A、B两点相当于架设两个定滑轮,直绳两端张力分别等于链绳两端张力大小.

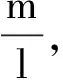
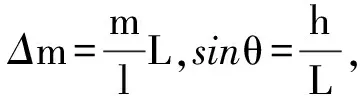
1.3 虚功原理

本题也可用虚功原理求解,虚功原理∑Fiδri=0,表示物体在力系作用下处于平衡状态,若由于其他原因使物体产生符合约束条件的连续微小虚位移δri,则所有主动力(外力和内力)在虚位移上所做的虚功为零.这是由伯努力1717年提出的,到1764年拉格朗日进一步完善.[1]由于高中生已接触一些基础的导数和微积分思想,在中学教学中渗透虚功原理思想是可行的.

图5 微小虚位移

2 动力学分析

3 方法比较评析

牛顿定律及在此基础上的理论为牛顿力学(也称矢量力学),拉格朗日方程及此理论基础上的理论为拉格朗日力学(也称分析力学),[2]下面对4类不同教学思路比较评析.

(1) 解法1是牛顿力学法,原则上所有的静力学问题都可由此方法解决．本题研究对象为曲线,若用常规解法学生还不具备高等数学水平,找不准重心位置、算不出角度大小,无从下手.“微元积累”思路上虽可行,但需画出复杂受力图，列方程组,数形结合能力要求高,只适合少数高水平学生.

(2) 解法2采用补偿法,实现模型等效转换,将模型化曲为直,化陌生为熟悉,运用基本方法即轻松解决,通俗易懂,此思路最妙,此法适合所有层次学生.

(3) 解法3虚功原理是分析力学中的重要方法,新颖独特,学生感叹有如此神奇的方法,脑洞大开,对启发学生创造性思维作用显著,解法1和解法3推荐给今后有物理研究方向的学生.

(4) 第(2)问求绳瞬时加速度采用功能关系同样非常巧妙,和解法1比避开复杂作图，列方程组,用功能关系列方程找出速度与微位移关系,间接求出了加速度,和解法3异曲同工.

(5) 解法3和第(2)问解法都用了图5进行分析,难道思想方法相同吗?虚功原理只适用处于平衡状态的物体系,解法3可用.而求瞬时加速度是动力学问题,虚功原理显然行不通,采用的是功能关系.功能关系既可用于静力学问题,又可用于动力学问题,适用范围更广.

(6) 以上解法表明,当研究对象特殊,牛顿力学方法不可行时,学生应采用能量方法如虚功原理和功能关系.

4 多样化教学启示

对均质链绳这一类经典力学问题的分析,在习题教学中,要有意识地拓展分析思路与方法,不应局限于某种方法,举一反三,在教学中拓展,引申如微元积累、补偿法、虚功原理、功能关系等重要规律和方法辅助分析,可高效拓展学生的分析思维,激发学生学习的积极性,优化创造性思维品质,提高综合运用知识的能力.