基于极大代数的MVB网络过程数据通信建模与分析
2018-10-09胡黄水常玉琪王宏志
胡黄水, 常玉琪, 王宏志, 王 博
(1. 长春工业大学 计算机科学与工程学院, 长春 130012; 2. 长春市轨道交通集团有限公司, 长春 130012)
多功能车辆总线(MVB)是一种应用广泛的列车通信网络, 列车的速度、 加速度等运行状态均可通过其过程变量直接反映, 而过程变量可用过程数据直接表示. 过程数据传送时间必须短而确定, 因此它被周期发送, 是无确认的广播信息. 由于过程数据的传输时延具有不确定性, 而数据的无阻塞通信是保证列车正常可靠运行的基础, 因此, 对过程数据通信的可靠性研究具有重要意义[1-3].
为有效提高MVB网络过程数据通信的实时性和可靠性, 文献[4]构建了一种分布均匀的实时调度表; 为获取过程数据受哪些通信参数影响, 文献[5]通过排队理论对其与传输速率、 轮询周期等之间的关系进行了深入分析; 文献[6]采用Petri网建模方法, 通过建立过程数据通信模型, 对过程数据通信过程中的数据传输能力、 网络吞吐量及带宽利用率等进行了大量测试与分析. 目前的提高过程数据传输可靠性方法多是通过设计调度算法从而优化周期扫描表实现. 本文基于极大代数方法, 通过建立过程数据通信数学模型(该模型面向开环总线型MVB网络), 引入周期输入控制, 讨论在确定时间参数下, 过程数据传送系统是否可控、 系统是否会进入周期稳态以及在何种条件下系统无阻塞, 并通过计算和仿真分析过程数据的通信阻塞性.
1 基本原理
1.1 过程数据通信
MVB网络通信采用主从工作方式[7], 其通信过程如图1所示. 首先, MVB网络主设备的总线管理器(bus administrator, BA)从通信存储器中周期读取主帧(其功能码F_code取值为[0,4]), 且该周期值固定; 然后BA将该主帧向总线广播, 对设备中地址与主帧所指向地址相同的(即源设备)做出响应, 其从通信存储器中读取从帧, 并发送至总线, 该从帧被网络中寻址的宿设备接收.

图1 MVB网络过程数据通信Fig.1 Process data communication of MVB network
1.2 极大代数方法
极大代数方法常用于离散事件动态系统, 极大代数定义为
(1)

(2)
其中
⊕ai2b2j⊕…⊕aipbpj,
∑⊕可记为∑. 相应地, 矩阵A的k次幂为Ak=AAk-1.
过程数据在MVB网络中通过在总线段和从设备节点间进行传输, 可将MVB过程数据通信的三要素MVB总线段、 从设备节点及过程数据构成一个离散事件动态系统, 则过程数据占用MVB总线段和从设备节点可作为一个事件. 因此, 极大代数方法可用于对MVB过程数据通信过程进行分析和研究.
MVB网络通信系统为总线型网络, 为保证其正常工作, 规定某一时刻只能有一个过程数据占用某个MVB从设备或MVB总线段, 因此可将MVB网络通信系统视为一个缓冲容量为1的刚性生产线系统. 由于过程数据在MVB从设备节点和MVB总线段的处理时间上规律性较强, 因此构建一个矩阵T, 其元素表示一个过程数据报文传输时间, 记为T=(t1,t2,…,tn).
2 系统模型
设u(k)表示BA在通信存储器中读取第k个主帧的时刻,xi(k)表示第k个过程数据从源设备i读取从帧并发送到第i个总线段结束的时刻,y(k)表示第k个过程数据结束一次完整通信过程的时刻, 即该过程数据不再占用MVB总线的时刻. 用向量表示为: 状态向量
X(k)=(x1(k),x2(k),…,xn(k))′;
输出向量Y(k)=y(k); 输入向量U(k)=u(k). 因此, 第k个过程数据完成一次完整通信所需时间为
Tk总=y(k)-x1(k).
由于只能有一个过程数据占用MVB从设备节点或MVB总线段, 而实际过程中可能出现相邻的两个过程数据发生冲突需要等待的情况, 因此对于某个特定的过程数据, 需分等待与不等待两种情形考虑:
1) 对于第k个过程数据, 如果第(k-1)个过程数据并未占用第i个MVB总线段或从设备节点, 则只要该过程数据在第(i-1)个MVB总线段或从设备节点作业完毕后, 即可占用第i个MVB总线段或从设备节点, 从而有
xi(k)=ti-1⊗xi-1(k);
2) 当第k个过程数据在第(i-1)个MVB从设备节点和总线段上的作业结束时, 而其前一个过程数据依然占用第i个MVB从设备节点或MVB总线段, 则其需要等待前一个过程数据不再占用第i个MVB总线段或从设备节点, 从而有
xi(k)=0⊗xi+1(k-1).
由于BA以固定周期读取主帧, 因此某个过程数据完成一次广播到下次总线管理器读取主帧之间存在一个时间差τ, 从而有
xi(k)=τ⊗xi+1(k-1).
于是可采用两种形式表示第k个过程变量在任一总线段或从设备节点i的开始作业时间, 用公式表示为
xi(k)=max{ti-1+xi-1(k),0+xi+1(k-1)}=ti-1⊗xi-1(k)⊕0⊗xi+1(k-1),
(3)
xi(k)=max{ti-1+xi-1(k),τ+xi+1(k-1)}=ti-1⊗xi-1(k)⊕τ⊗xi+1(k-1).
(4)
当i=1时, 表示第一个从设备节点或总线段被第k个过程数据开始占用, 此时必满足第(k-1)个过程数据已不再占用第一个从设备节点, 有
x1(k)=max{0+u(k),τ+x2(k-1)}=0⊗u(k)⊕τ⊗x2(k-1);
(5)
当i=n时, 即第k个过程变量最早占用最后一个区间时, 应满足:
xn(k)=max{tn-1+xn-1(k),tn+xn(k-1)}=tn-1⊗xn-1(k)⊕tn⊗xn(k-1).
(6)
因此, 系统的状态方程和输出方程为
(7)
其中: 矩阵A表示第k个过程数据占用前后两个MVB从设备节点与MVB总线段时刻之间的关系; 矩阵B表示读取主帧时刻与第k个过程数据开始占用MVB总线段或从设备节点时刻之间的关系; 矩阵F表示第k个过程数据的当前作业时刻与(k-1)个过程数据所处作业状态之间的关系; 矩阵C表示第k个过程数据作业结束时刻与其占用各从设备节点或MVB总线段时刻之间的关系. 各矩阵用公式表示如下:
(8)
下面对矩阵A执行A*运算, 则系统状态方程(7)将发生变化, 表示为
(9)
其中: 矩阵A*F表示第k个与其前一个过程数据二者状态之间的关系; 矩阵A*B表示第k个过程数据状态与其最早占用MVB网络总线时刻之间的关系. 根据式(9)对式(7)进行简化. 矩阵A*F,A*B分别表示为
(10)
由上述表达式可知, 报文传输时间矩阵T中各值将决定系统的所有状态.
3 性能分析
3.1 周期输入控制
IEC协议对MVB基本和特征周期进行了规范, 其中前者是主设备完成一次轮询所需的时间, 后者是同一过程数据从同一个源设备两次连续发送的间隔时间, 且固定轮询时间和过程数据通信间隔必须得到保证. 为了实现该目标, 可引入周期输入控制MVB过程数据通信系统的稳定无阻塞.

定义2假设λ≠-∞, 并存在某个正整数n0, 使得∀n>n0,Ad+n=λdAn, 则称A为d阶λ周期阵. 其中的乘法为一般意义的加法,λd即为普通的dλ[9].
对于任意正整数n, 将周期输入控制引入式(9):
X(n)=X(0)(A*F)n⊕U(0)A*B(μE⊕A*F)n.
(11)
由式(11)可知, MVB网络过程数据通信系统的状态量取决于矩阵A*F和μE. 为方便分析, 将T中的报文传输时间均加上一个时间差τ构成一个新的时间矩阵T′, 该时间差τ表示前一个过程数据完成一次通信过程的时刻到下一次主帧被读取时刻之间的时间差.A*F和μE⊕A*F均为周期阶数为1的周期阵[10],A*F特征值为T′中的最大值,μE⊕A*F的特征值若设为ω, 则当μ≤max{T′}时,ω=max{T′}; 当μ>max{T′}时,ω=μ.
假设λ为矩阵A*F的特征值,λ=max{T′}, 则当μ≤λ时必存在n1, 且对于任意n>n1, 均有X(n+1)=λX(n); 当μ>λ时, 必存在n2, 对于任意n>n2, 均有X(n+1)=μX(n), 且n2必小于或等于矩阵μE⊕A*F的维数. 通过引入周期控制, 使得MVB网络过程数据通信系统的状态量和输入量Y(k)=C⊗X(k)都进入周期为1的周期稳态, 而时间矩阵T′中的最大值决定了其参数.
3.2 网络阻塞性分析
通过上述模型可知, 若使MVB网络过程数据通信无阻塞, 则过程数据在前一个MVB总线段中运行完毕的时间应为下一个MVB从设备节点开始作业的时间, 需满足:
xi(k)=ti-1⊗xi-1(k)≥xi+1(k-1).
(12)
且必须考虑前一个过程数据作业结束到下一次BA读出主帧之间的时间差τ, 则
xi(k)=ti-1⊗xi-1(k)≥τ⊗xi+1(k-1).
(13)
状态方程可表示为
X(k)=A⊗X(k)⊕B⊗U(k)或X(k)=A*B⊗U(k).
综合上述分析可知, 若使过程数据通信网络无阻塞, 则需满足∀i∈{1,2,…,n}, 均有
U(k)≥T′(i)+U(k-1),
即BA在通信存储器中读取主帧的时间间隔不小于T′中的最大值.
4 仿真实验
由于MVB网络中任意两节点间进行过程数据通信的传输时延不大于42.7 μs, 且连续的两个报文之间延时差值应小于或等于4.0 BT(1.0 BT≈666.7 ns), 即两两报文之间的差值不超过4.0 BT, 任意两个主帧间隔不小于9.0 BT, 因此, 某过程数据在MVB总线上完成一次通信到下一次在通信存储器中读取主帧的时刻两者之间的时间差τ最大为5.0 BT[11]. 但在实际过程数据通信中, 不可避免地存在传输延时波动, 从而减小帧与帧之间的时间间隔, 于是发生阻塞或帧间重叠. 下面针对该问题对MVB网络过程数据通信模型的阻塞性进行分析, 实验选取过程数据的10次轮询, 并令其特征周期均为基本周期, 观察连续两个过程数据作业时间关系判断是否发生阻塞现象. 图2为过程数据工作时刻比较. 由图2可见, 第k和(k-1)个过程数据并未发生重叠, 因为前者开始工作的时刻并未与后者结束的时刻出现重叠. 图3为过程数据通信过程的时刻差.

图2 过程数据工作时刻比较Fig.2 Comparison of working time of process data
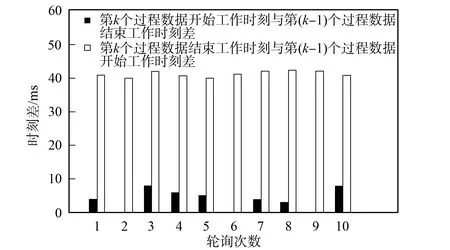
图3 过程数据通信过程的时刻差Fig.3 Time discrepancy in process data communication
由图3可见, 第k个过程数据开始工作时刻与第(k-1)个过程数据结束时刻的差值始终保持为正数, 说明两个连续帧之间未出现阻塞, 即通信过程未出现阻塞.
综上可见, 在满足IEC标准的前提下, 本文采用极大代数方法, 通过对过程数据通信建立数学模型, 并引入周期输入控制, 计算出当BA在通信存储器中读取主帧的时间间隔大于或等于过程数据时间矩阵中的最大值时, 不会发生阻塞. 在满足上述条件下, 对该方法进行了仿真测试, 结果表明, MVB过程数据通信过程无阻塞, 保证了其通信的可靠性.
