基于Signature和Ⅱ型双删失系统寿命数据的统计推断
2018-10-09冯海林
冯海林, 郭 甜
(西安电子科技大学 数学与统计学院, 西安 710071)
在可靠性寿命测试中观测得到的数据形式有两种, 分别是组成系统各元件的寿命和系统的寿命[1]. 对结构确定的系统, 实验中只能观测到系统的寿命, 即当系统工作至失效时, 无法确定哪一个元件导致系统失效. 另一方面, 对单独元件的寿命实验, 将各元件配置在系统中并对该系统进行寿命测试, 不仅可节约实验时间, 同时所测试的寿命数据也包含了组成系统各元件之间的相关信息. 因此, 基于系统寿命数据对元件寿命分布的统计推断有一定的意义[2].
在关联系统的背景下, Samaniego[3]提出了Signature的概念, 它不仅能给出系统的结构信息, 并且可以将系统寿命的可靠性函数表示为元件次序寿命的可靠性函数与Signature向量的混合. 在元件寿命的参数估计方面, Bhattacharya等[1]基于系统失效寿命数据, 讨论了经验元件分布的参数估计, 并推断了元件的重要度; Ng等[4]基于Signature已知的系统寿命数据, 针对元件寿命为比例失效率(PHR)模型的情况, 给出了元件寿命分布的参数估计. 在元件寿命分布的非参数推断方面, Balakrishnan等[5]使用系统寿命的次序统计量, 研究了元件寿命分布分位点的精确非参数置信区间, 并讨论了元件寿命分布分位点的置信下限和双侧置信限; Volterman等[6]考虑了系统失效数据的融合, 将两个或两个以上具有不同Signature的系统联立, 基于大量系统的寿命数据, 给出了元件寿命的准确联合非参数推断. 以上统计推断均基于完全寿命实验, 即进行到所有的系统完全失效, 为节省时间和成本, 可采用删失寿命数据进行统计推断. Balakrishnan等[7]通过考虑Signature已知的可靠性系统的Ⅱ型右删失寿命数据, 研究了当元件寿命属于一般尺度参数族和位置-尺度参数族时, 元件寿命分布参数的最优线性无偏估计, 并进一步讨论了系统失效时间的最优线性无偏预测; 文献[8]将其拓展到线性统计推断中, 对大量Monte-Carlo(MC)仿真的Ⅱ型右删失系统失效数据, 给出了Signature已知时元件寿命分布的位置-尺度参数的极大似然估计和基于回归的估计, 结果表明, 这些估计优于前面的最优线性无偏估计; 文献[9]结合结构已知的完全系统寿命和删失系统寿命数据, 使用随机最大期望(EM)算法获得了相关参数的极大似然估计(MLE), 并证明了该算法对多种元件寿命分布族都适用.
对于一个实际运行的系统, 由于条件所限或记录延迟等原因, 可观测到的寿命数据更多是Ⅱ型双删失样本数据, 即前(l-1)个和后(m-r)个数据删失, 此时观测到的寿命数据次序统计量为
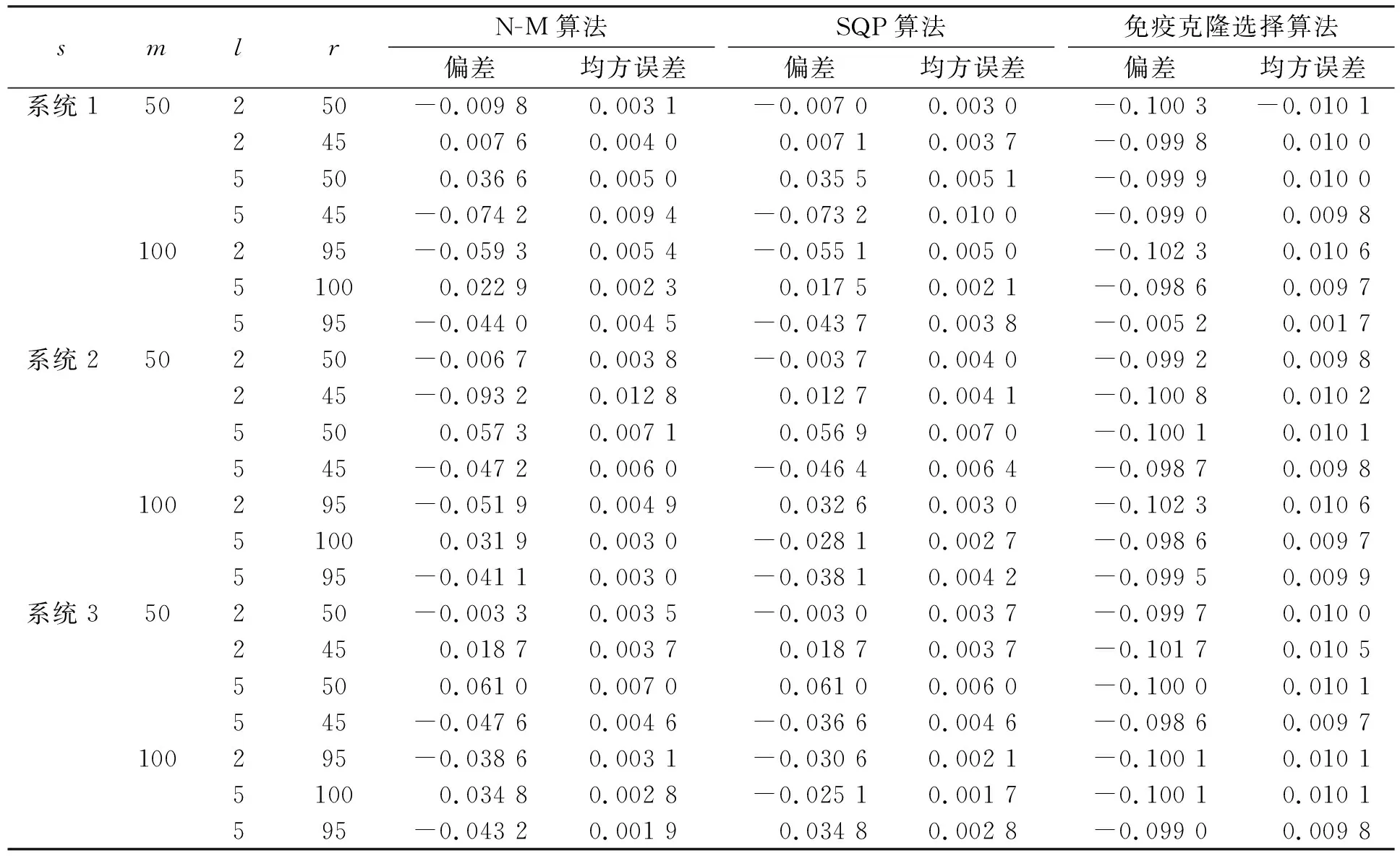
Tl ∶m 这类数据在实际生活中广泛存在[10]. 因此, 针对Ⅱ型双删失寿命数据元件寿命分布的统计推断更有实际意义. 本文针对Signature已知的系统, 基于Ⅱ型双删失系统寿命数据, 在元件寿命分布为位置-尺度分布族情形下, 给出元件寿命分布的统计推断结果, 并以Weibull寿命分布做验证, 即通过MC仿真实验模拟产生系统寿命样本, 分别设计N-M算法、 SQP算法和免疫克隆选择算法实现点估计的结算, 最后给出参数的渐近置信区间估计. (1) 引理1表明, 当系统的Signature已知时, 可用系统寿命数据实现对系统元件寿命分布参数的推断. 由引理1, 系统寿命T的概率密度可表示为 (2) 特别地, 当元件寿命X的概率密度函数为 (3) 时, 可得系统寿命的概率密度函数为 (4) 首先给出元件寿命分布参数的点估计. 假设对m个系统进行寿命测试实验, 每个系统由独立同分布的n元件构成, 前(l-1)个系统寿命数据丢失, 观测得到第l~r个系统的失效时间, 即得到一个Ⅱ型双删失样本 tl ∶m 其中l,r分别为左、 右删失数量,l/n和r/n为样本双侧删失比. 基于上述系统寿命数据, 令θ=(μ,σ)′为参数向量, 则θ的似然函数为 相应的对数似然函数为 其中c是一个不依赖于参数的常数. 将式(6)中系统寿命的PDF,CDF,SF分别由等式(1),(2)替换可得 为了给出参数θ=(μ,σ)′的极大似然估计, 先对似然函数式(5)或对数似然函数式(6)取最大值, 再对其求解. 式(6)的一阶、 二阶偏导分别为 为计算系统寿命分布的偏导函数式(8),(9), 需先计算下列系统寿命分布的PDF和SF对相应位置-尺度参数的局部偏导: 在点估计结果的基础上, 可给出参数的渐近置信区间估计. 由式(9)计算得到局部Fisher信息矩阵为 (14) 参数极大似然估计的方差-协方差矩阵为 (15) (16) (17) 其中,zq为标准正态分布的第q个上分位点. 由于参数σ≥0, 故可修正置信区间为 (18) 理论上, 参数的极大似然估计需要求解下列似然方程组: (19) 显然式(19)是超越方程构成的似然方程组, 对复杂的元件寿命分布如Weibull分布, 其直接求解相当复杂甚至不可能. 按照极大似然原理, 似然函数极大化问题即为下列函数的极小化问题: min{-l(θ;tl ∶m,t2∶m,…,tr ∶m)}, (20) 式(20)是一个复杂的多维非线性无约束问题. 本文设计3种优化算法求解该问题. 1) Nelder-Mead算法(简称N-M算法), 即沿着使目标函数值下降的方向逐步逼近最优解; 2) SQP算法(或称序列二次规划法), 即为了减少计算量, 将对数似然函数的梯度信息加入到优化求解中, 用一系列的线性规划或二次规划逐次逼近原非线性规划问题的最优解; 3) 免疫克隆选择算法, 即为避免初始值对迭代结果的影响, 将抗体亲和力对应于似然函数模型(7), 抗体即为参数估计值. 设定一定的抗体群规模, 抗体初始化时, 随机产生一代抗体, 计算亲和力大小. 在一代进化中, 根据亲合力大小, 对抗体进行选择、 克隆和变异操作, 得到一组子抗体群, 并对其进行再选择, 筛选出新一代抗体, 设定一定迭代次数后, 将最后一代抗体群中的最优抗体作为最优解输出. 仿真的软件环境为Windows7, 64位操作系统和MATLAB R2014a; 硬件环境为Intel Core i5-3230处理器, 4 GB内存. 本文针对Navarro等[12]提出的3种不同Signature系统, 进行MC(Monte Carlo)仿真研究, 仿真实验设置中, 根据m的大小, 将仿真分为小样本和大样本两种情况. 其中: 系统1是一个四元件串并联Ⅲ系统, 系统Signature为s1=(1/4,1/4,1/2,0); 系统2是一个四元件混合并联Ⅰ系统, 系统Signature为s2=(0,1/2,1/4,1/4); 系统3是一个三元件并串联系统, 系统Signature为s3=(0,2/3,1/3). 仿真实验实例选取系统的元件寿命W为Weibull分布 (21) 其中:β>0是尺度参数;α>0是形状参数. 则随机变量X=lnW服从最小极值(SEV)分布, CDF和PDF分别为 (22) (23) (24) (25) 仿真过程如下: 1) 产生系统Signature为s=(s1,s2,…,sn)、 元件寿命为Weibull分布的m组系统寿命数据T1∶m ① 由一个离散n点分布、 以概率P(V=v)=sv(v=1,2,…,n)产生一个随机数v; ② 由次序统计量的性质, 从正态分布产生第v个次序统计量U(v), 其中U(v)服从参数为v和m+1-v的Beta分布; 2) 设定左右删失量l和r(1 3) 分别用N-M算法、SQP算法、 免疫克隆选择算法求解式(20), 得到参数的点估计与区间估计. 4) 设定不同大小的样本容量和左右删失数, 重复过程1)~3). 5) 重复步骤1)~4)共10 000次, 并计算点估计值的偏差(Bias)和均方误差(MSE), 以及各区间估计的95%置信区间的覆盖率(CR)和平均覆盖宽度(ACI). 设寿命实验中有m=10个样本系统, 元件寿命的Weibull分布中参数, β=3, α=2, 则对数转换后对应的位置、 尺度参数分别为μ=ln3, σ=1/2. 设寿命样本的左删失率p=10%, 即l=2, 令右删失率q分别为10%,20%,…,70%, 即r=m(1-q)=9,8,…,2, 则可得3种不同Signature下参数μ和σ的点估计与区间估计的仿真结果分别如图1和图2所示. 图1 l=2时元件寿命位置参数μ的点估计与区间估计结果 Fig.1 Point estimation and interval estimation results of component lifetime location parameter μ when l=2 由图1和图2可见:N-M算法区间估计的平均宽度可稳定在较小的值, 但对区间估计的覆盖率较低, 在对σ的估计中, 区间估计的覆盖率明显低于其他两种算法;SQP方法点估计的均方误差最小, 区间估计覆盖率大, 但随着删失率的增大, 还能保证较高的覆盖率, 同时区间的平均宽度也较大; 免疫克隆选择算法在对μ的点估计中, 偏差均为负且可以收敛到0, 区间删失率较低时能保证较高的覆盖率, 但随着删失率增大, 覆盖率下降很快. 在算法迭代过程中,N-M算法对初值的选择较敏感, 数值迭代过程中需要选择适合的初始值; 免疫选择算法随机生成初始参数值, 通过数值迭代选择, 逐步寻找到最优的估计值, 对初始值不敏感, 鲁棒性强;SQP算法给出的位置参数和尺度参数的点估计和区间估计效果最好, 精度更高. 图2 l=2时元件寿命位置参数σ的点估计与区间估计结果Fig.2 Point estimation and interval estimation results of component lifetime location parameter σ when l=2 设寿命实验中有m=50和m=100个系统, 本文列举了左右删失数不同7种情况下3种不同算法对不同Signature的仿真结果, 点估计与区间估计结果分别列于表1~表4. 表1 大样本下N-M算法、 SQP算法及免疫克隆选择算法对参数μ的点估计结果 表2 大样本下N-M算法、 SQP算法及免疫克隆选择算法对参数σ的点估计结果 表3 大样本下N-M算法、 SQP算法及免疫克隆选择算法对参数μ的区间估计结果 表4 大样本下N-M算法、 SQP算法及免疫克隆选择算法对参数σ的区间估计结果 表5 10 000次仿真下3种算法的平均运行时间(s) 表6 Signature分别为s1,s2,s3, 元件寿命服从Weibull (3,2)分布的系统寿命结果 设左、 右删失数分别为l=2和r=9, 通过3种不同优化算法得到元件寿命分布参数的点估计与区间估计结果列于表7. 由表7可见: 由SQP算法得到的点估计方差最小, 进一步得到的置信区间估计最精确; 免疫优化算法不用设定初始值, 对不同寿命数据下参数的优化结果值差异不大. 实验结果验证了大样本和小样本情形下的参数估计结果. 表7 对表6中系统寿命数据的估计结果 综上, 本文在Ⅱ型双删失系统寿命数据下, 研究了基于系统Signature的元件寿命分布参数的统计推断问题, 使用极大似然估计及其渐近理论给出了参数的点估计和渐近置信区间估计, 并设计了优化计算似然函数的N-M算法、 SQP算法和免疫克隆选择算法. 以元件寿命为Weibull分布为例, 分别给出了小样本和大样本实验数据下的估计结果, 表明SQP算法给出的参数估计效果最好. 随着样本量的增大, 基于Ⅱ型双删失样本的似然函数偏导表达式更复杂, 虽然估计精度和效果会随着样本数据的增大而提高, 但也会使点估计的方差和协方差计算量更大, 进而使区间估计的计算变得繁琐, 针对此问题, 本文设计的3种优化算法均能有效解决, 并得到了较准确的点估计和区间估计结果.1 基于Signature的系统可靠性函数

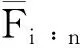

2 基于Signature的系统元件寿命参数推断
2.1 元件寿命参数的似然估计
2.2 元件寿命参数的渐近置信区间估计
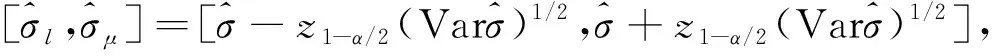
2.3 参数估计的优化算法设计
3 MC仿真实验



3.1 小样本仿真


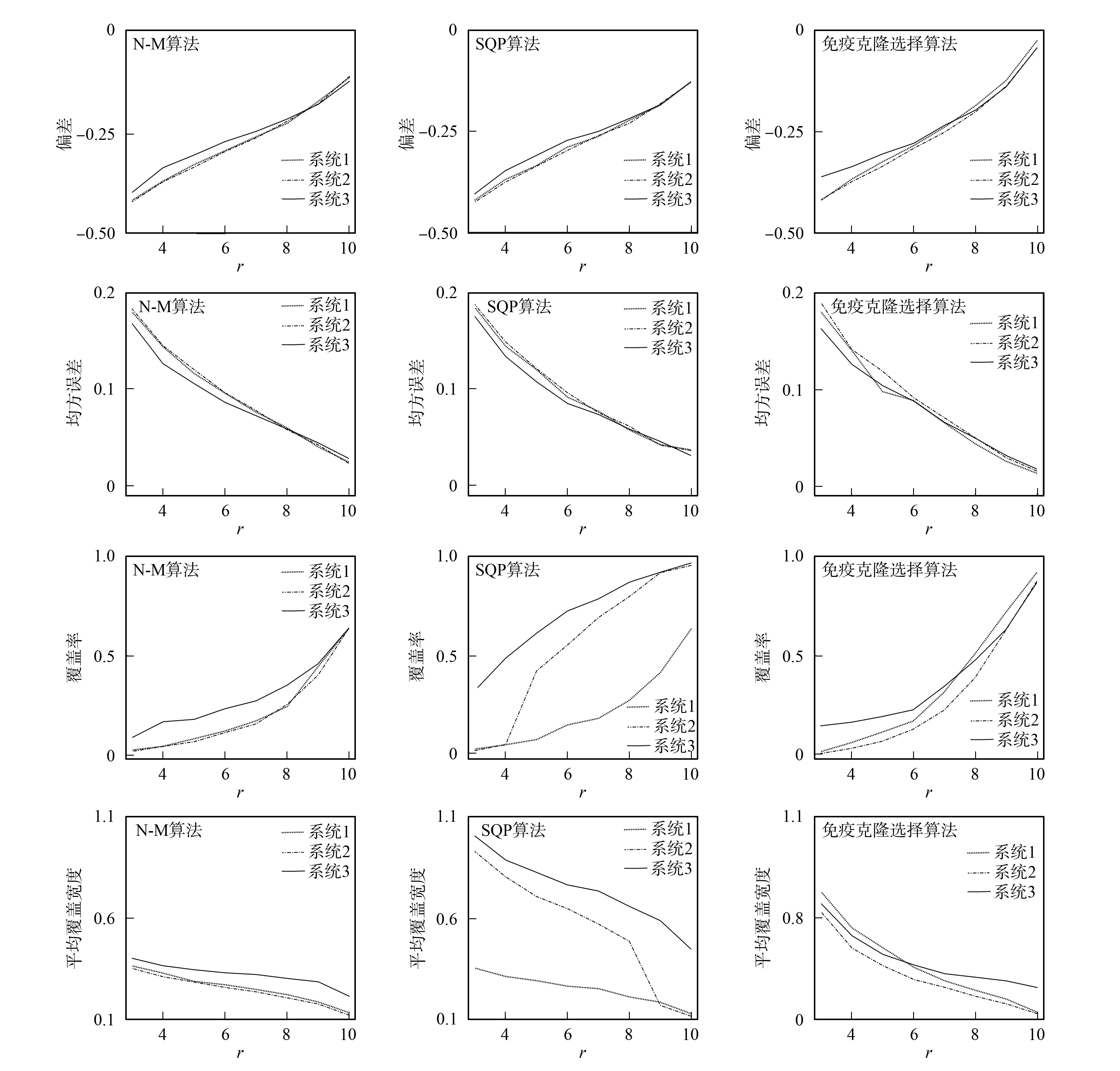
3.2 大样本仿真





4 实例分析



