U-统计量精确渐近性的注记
2018-10-09高云峰谭希丽
高云峰, 谭希丽
(1. 吉林农业科技学院 文理学院, 吉林 吉林 132101; 2. 北华大学 数学与统计学院, 吉林 吉林 132013)
1 引言与主要结果

(1)
其中h(x,y)为对称核函数. 记
μ=Eh(X1,X2)=0,h1(x)=Eh(x,X2),h2(x,y)=h(x,y)-h1(x)-h1(y).
U-统计量是算术平均值的自然推广, 在概率论与数理统计中应用广泛. 目前, 关于U-统计量大样本性质的研究已有很多结果[2-9].
假设条件:
(H1)g(x)为[n0,∞)上具有非负导数g′(x)的正值可导函数, 且g(x)↑∞,x→∞;




本文的主要结果如下:

(2)
如果假设条件(H1),(H2),(H3)成立, 则对于q>s-1>1, 有
(3)
如果假设条件(H1),(H2)成立, 则对于q>s-1>1, 有
(4)

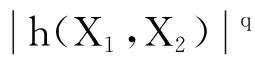
(5)
如果假设条件(H1),(H3)成立, 则对于s>0, 有
(6)
注1满足假设条件(H1)~(H5)的g(x)有很多, 如g(x)=xα,(logx)β,(loglogx)γ等, 其中α>0, β>0, γ>0为某些适当的参数.
注2显然式(4)和式(6)分别为文献[15]中定理2.1和定理2.2的结果. 在式(4)中令s-1=2(r-p)/(2-p), g(x)=xr/p-1, 其中1 设C表示正常数, 不同之处可表示不同的值. 令a(ε)=[g-1(Mε-1/s)], 其中: g-1(x)为g(x)的反函数; M≥1. 命题1定义U-统计量如式(1), 且满足定理1的假设条件. 如果假设条件(H1),(H2)成立, 则有 证明: 利用引理1和引理2, 类似文献[11]中定理2.1, 可知结论成立. 命题2定义U-统计量如式(1), 且满足定理1的假设条件. 如果假设条件(H1),(H2),(H4)成立, 对于q>s-1>p>0, 则有 证明: 类似文献[18]中命题5.1的证明. 命题3定义U-统计量如式(1), 且满足定理1的假设条件. 如果假设条件(H1),(H2),(H4)成立, 对于q>s-1>p>0, 则有 (7) 证明: 显然 其中: 根据引理1和引理3, 当n→∞时, Δn→0. 首先估计Δn1: 由于n≤A(ε)即εgs(n)≤Ms, 从而有 其次估计Δn3: 由正态分布的性质, 可知 最后估计Δn2: 由引理2, 注意到q>1/s>p>0, 有 因此由式(8)~(11), 可得 Δn1+Δn2+Δn3→0,n→∞. (12) 进而由式(12)、 φ(x)的单调性以及Toeplitz引理[19], 可知式(7)成立. 证毕. 命题4定义U-统计量如式(1), 且满足定理1的假设条件. 如果假设条件(H1),(H2),(H4)成立, 对于q>s-1>p>0, 则有 证明: 注意到q>s-1>p>0, 由引理2, 有 命题5如果假设条件(H1),(H2),(H4)成立, 对于q>s-1>p>0, 则有 证明: 利用正态分布的性质, 类似命题4可证该结论成立. 当p=0时, 由于 则由命题1可知定理1成立. 当s-1>p>0时, 注意到 故要证明式(2), 只需证明下列两式成立即可: (13) (14) 由命题1可知式(13)成立. 由命题2~命题5以及三角不等式可证式(14)成立, 从而式(2)成立. 式(3)和式(4)的证明类似. 定理2的证明与定理1的证明类似, 故略.2 定理的证明

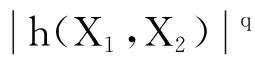

2.1 定理1的证明


2.2 定理2的证明
