基于地貌参数的泥石流沟发育阶段划分*

赵 岩，孟兴民,2，庆 丰，刘林通，郭富赟,3

(1.兰州大学 资源环境学院 西部环境教育部重点实验室，甘肃 兰州 730000；2.甘肃省环境地质与灾害防治工程研究中心，甘肃 兰州 730000；3.甘肃省地质环境监测院，甘肃 兰州 730050)

泥石流发源于地貌学[1]，说其特殊因为它是一种主要由水和重力作用引发的强烈的地表流水侵蚀、搬运与堆积的过程[2]；而说其不特殊是因为泥石流活动属于地貌演化过程中众多夷平作用过程的其中一种。既然泥石流活动属于地貌演化的一种形式，而地貌演化是分阶段的，所以泥石流沟的发育阶段也可以通过地貌参数来定量划分。本文通过分析与泥石流发育阶段相关的地貌参数，将泥石流沟的发育阶段进行定量划分。

1 地貌信息熵与超熵的应用与来源

1.1 地貌信息熵与超熵的应用

地貌信息熵(H)与超熵(∂xP)被应用到了许多领域的研究中。刘小凤等[3]将H应用在了构造活动和区域稳定性评价；铁永波等[4]将H应用在泥石流沟谷的危险性评价研究中；孙然好等[5]将H应用在山体演化阶段的判定；王晓朋等[6]利用H来判断泥石流的发育程度，用于定量评价泥石流危险性；李雅辉等[7]基于H对泥石流敏感性进行定量评价；岳俊生等[8]将∂xP应用在泥石流发育现状及其危险度评价；邹强等[9]将∂xP应用在泥石流活跃度的定量分析；王钧等[10]将H应用在震后泥石流危险性评价；刘丽娜等[11]利用H进行泥石流危险性评价；张宝军等[12]将H应用在冲沟沟头活跃度的判定。H和∂xP的广泛应用，有必要对其来源及其与泥石流发育阶段的关系进行分析与讨论。

1.2 地貌信息熵与超熵理论来源

1899年，Davis[13]提出地貌循环理论，并将地貌演化阶段分为幼年期、壮年期和老年期三个阶段，1952年Strahler[14]提出侵蚀流域的面积高程分析方法，并用曲线积分值S的大小来划分侵蚀流域地貌演化阶段：S>0.6时为幼年期，0.35≤S≤0.6时为壮年期，S<0.35是为老年期，从而将戴维斯的地貌发育模型定量化。面积高程积分值S的计算方法如下。

设A表示流域面积，a表示该流域内某条等高线上的面积，h表示该等高线与流域内最低点的高差，ΔH表示流域内最大相对高差，则对直角坐标轴上一系列X=a/A，Y=h/ΔH组成的点进行拟合，得到拟合效果最好的函数y=f(x)即为面积高程积分曲线，而其积分即曲线包围的面积，称为面积高程积分值：

(1)

由于地貌系统演化过程的数学描述与热传导方程相似，1962年里奥普和拜里把熵的概念引入地貌学中。1970年Leopold与Langbein也提出过地貌学熵的定义，热力场是由温度T(x,y)和热量Q来表现，地貌场类似可以用高度h(x,y)和质量M表现，进而提出地貌学熵的定义：

ds=dQ/T⟺dM/h。

(2)

1987年我国学者艾南山[15]以Davis地貌循环理论、Penck的内外营力同时作用的地貌发育模型以及Shannon的信息熵理论，将熵的概念和计算方法引入到Strahler曲线和积分中，提出了侵蚀流域系统的地貌信息熵理论并推导出其值H的计算公式，推导过程简述如下。

1948年Shannon[16]提出能够定量描述系统演化阶段的的信息熵概念：

(3)

后有人将其推广到连续情形(p(x)为密度函数)：

(4)

用面积高程积分曲线f(x)和面积高程积分值S构造密度函数：

(5)

将(1)式、(5)式带入(4)式便可得到地貌信息熵：

H=S-1-lnS。

(6)

在之后的研究中又将信息熵由侵蚀流域引入到一般流域，利用Иванов的河流纵剖面方程(式中，h为纵剖面上某点与河口的高差，l为纵剖面上某点距河口的距离，H和L分别为河源与河口之间的高差和水平距离，N为形态指数，且01时，剖面下凹) ：

h=H(l/L)N。

(7)

使用同样的方法推导出利用纵剖面形态指数N表示的一般流域的地貌信息熵公式[17]：

H=ln (1+N)-N/(1+N)。

(8)

在1989年为使其可以应用在一般的远离平衡态的耗散结构的流域系统内，引入了超熵的概念，并推导出公式(α、β为参数)[18]：

∂xP=[-βα3(α2-1)]/[α(-β-1)-3]。

(9)

1992年蒋忠信[19]提出以沟谷纵剖面形态指数N表达超熵数学式，并试用于泥石流沟的判别与活动性评价。

2 H和∂ xP与泥石流发育阶段的关系

从地貌信息熵和超熵的理论来源来看，其理论基础分别是Davis的侵蚀循环理论和Иванов的河流纵剖面方程，对应的定量化公式分别为(1)式和(7)式来计算面积高程积分值(以下简称S)和纵剖面形态指数(以下简称N)。可以看出S和N分别从侵蚀流域的演化和河谷纵剖面的演化两种不同的角度对地貌的演化过程进行定量描述。

而抛开推导过程中所包含的意义，由S(或N)到H、∂xP的推导中关键的一步是通过构建含有S(或N)的密度公式(公式5)带入到熵的表达式(公式4)中实现的，这种变换从数学角度来看只是对S和N做了一定的拉伸和转换使其表达方式符合了熵的表现形式(即将原本随地貌侵蚀演化过程递减的函数S转换为随地貌侵蚀演化过程递增的函数H)，而H、∂xP对地貌发育阶段的划分完全依据S和N对应公式计算出的H、∂xP值来划分的。所以地貌熵和超熵的公式只是对S和N做的一种变换，而之后的很多研究只关注到地貌熵和超熵的应用，却忽视了其来源S和N的应用。所以，对于泥石流沟发育阶段的研究，从应用的角度来看直接使用S和N值更为简便。

3 基于S与N的泥石流发育阶段划分

3.1 S、N划分泥石流发育阶段研究现状

S、N、H和∂xP被广泛应用的根本依据是这些参数能够反映泥石流沟的发育阶段，且不同阶段泥石流的活跃程度不同。而利用这些参数对泥石流沟的发育阶段进行定量的划分方面的研究还比较少。刘希林[21]讨论了泥石流沟谷与其横、纵剖面的演化关系；蒋忠信[19]通过∂xP的三个特征值将泥石流的发育阶段划分为五个阶段(表1)；蒋忠信[22]研究了泥石流沟谷纵剖面的形态特征与泥石流活动性的关系；吕学军等[23]根据面积高程积分值将泥石流发育阶段划分为五个阶段；李泳等[24]用比降曲线和面积高程曲线讨论了流域可能发生泥石流的曲线形态和演化趋势。倪华勇[25]采用面积高程分析法对泥石流流域地貌所处的发育阶段进行了判别。然而大多研究对泥石流沟发育阶段的判定都是根据Strahler的三个地貌阶段划分的。另外，蒋忠信对N的划分是根据数学意义上的特征点来确定的界限值，吕学军等对S的划分也是根据经验来确定的(表1)。

表1 各学者对泥石流发育阶段的定量划分的界限值

3.2 S、N计算方法与实际意义分析

首先讨论面积高程积分值S，由式(1)可知S实际上代表着坐标轴上一些列x=a/A，y=h/ΔH点的拟合曲线的积分值，这种利用定义计算S的方法称为积分曲线法。由积分定义可知，将x分为n等份则(其中V剩表示流域现有体积，V总表示未侵蚀时流域的总体积(图1))：

(12)

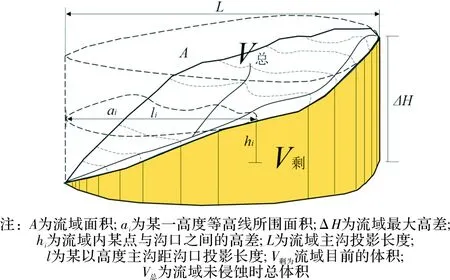
图1 S、N值计算各参数示意图

故S值的实际意义表示该流域经侵蚀后所剩体积占未经侵蚀时流域总体积的百分比，这种计算方法称为体积比法。Pike等[26]推算出用起伏比法来计算S(其中Hmean、Hmax和Hmin分别代表流域内平均高程、最大高程和最小高程)：

(13)

由于平均高程与最小高程之差表示流域的平均高差，最大高差与最小高差之差表示流域最大高差，故由式(11)也可以推出式(13)(其中A为流域面积)：

(14)

常直杨等[27]对体积比法和起伏比法计算方法的准确性也进行了验证，结果为三种方法计算出的S值几乎一致。

对于纵剖面形态指数N，其实是从主沟道的侵蚀状态来判断流域发育的所处阶段的。由S和N表达的地貌信息熵式(6)和式(8)让S和N建立了一定的联系，据蒋忠信的推导为：

S=1/(N+1)。

(15)

而这种关系是从两种地貌熵的形式变换得到的，实际中S和N到底其关系是不是如此还需要实例来进行验证，为此本文以白龙江流域为研究区，通过区内DEM进行水文分析共提取出1 984条流域，通过历史灾害资料的收集以及实地的调查共收录有泥石流灾害记录的泥石流流域714条(图2)，从中挑选流域内典型的泥石流沟对其流域的面积高程积分值和流域纵剖面形态进行对比。

图2 白龙江泥石流沟流域分布图

名称H/mL/mS值N值R21/(N+1)误差仁家沟157168860.690.7680.880.560.13马泉沟146445930.650.8490.960.540.11阴山沟116422210.60.8780.970.530.07三眼峪沟243586700.551.5210.990.400.15罗家峪沟237677890.511.3180.990.430.07旧房沟189861240.492.4030.970.290.2红土湾沟168969610.422.2500.940.310.11梨坪沟99523930.381.6160.980.380联丰沟149751220.322.5310.990.280.04段河坝沟117745370.233.3990.990.230王石坝沟84035050.213.9130.990.200.01

从表2和图3的结果我们可以看出，只有在纵剖面形态为比较规则的上凸或下凹曲线时，利用公式拟合的效果才比较好，得到的N值也与S值有较好的一致性，比如阴山沟、罗家峪沟、梨坪沟、联丰沟、段河坝沟、王石坝沟，而纵剖面的形态指数N会受到DEM精度、主沟道纵剖面精确性、纵剖面形态凹凸度、拟合公式局限性等众多因素的影响且计算繁琐，而利用DEM通过式(12)和式(13)来计算S值时受到其他因素的影响较小，结果较为可靠且计算便捷。

3.3 基于S的泥石流发育阶段划分

通过以上分析，使用S对泥石流沟发育阶段进行定量的划分是比较便捷和可靠的。S划分的幼年期、壮年期和老年期是针对侵蚀循环理论的，而对于泥石流沟的发育阶段的划分则要从泥石流发育特点来进行重新划分。从已有的研究来看泥石流的发育阶段划分为五个阶段更为详细和合理，分别为发育期、发展期、旺盛期、衰减期和消退期。

这里说的泥石流沟的发育时期应该是泥石流在同等条件(即抛开随机性较大的降雨等激发因素)下的泥石流的活跃程度或者说易发程度，所以并不能代表泥石流实际的活跃程度和规模大小，因为在实际条件下，泥石流的活跃程度受到物质条件的动态性、激发条件的随机性等的影响，其活跃程度会有着较大的区别。

然而现实条件下无法找到同等条件下且发育在不同时期的泥石流沟，所以我们选取泥石流多发的白龙江流域[28]内714条有泥石流记录的沟进行调查，得到550条泥石流沟的发生频率资料(图4)，通过统计分析得到石流发生频率与S值的关系(图5)。

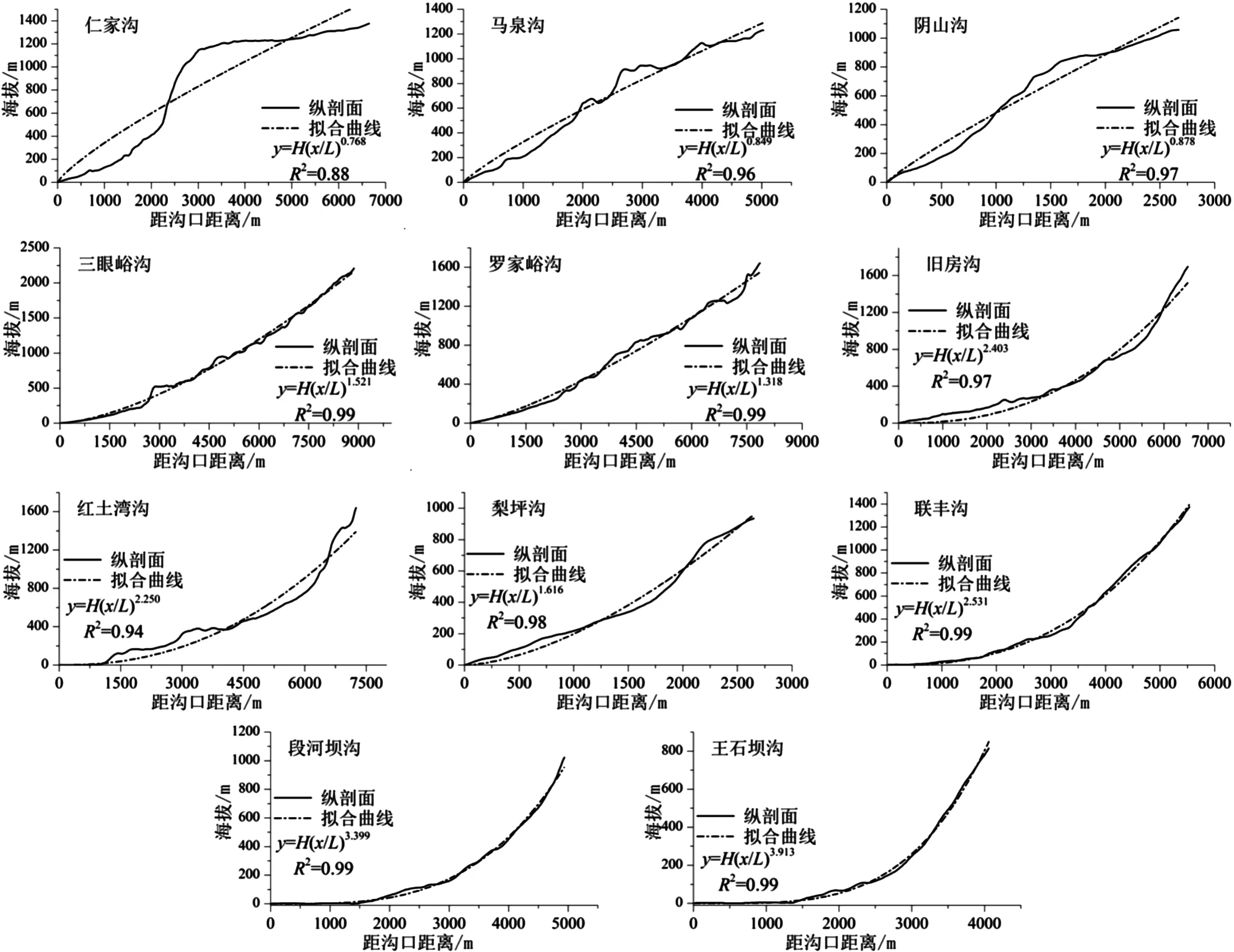
图3 各泥石流沟沟谷纵剖面及拟合曲线

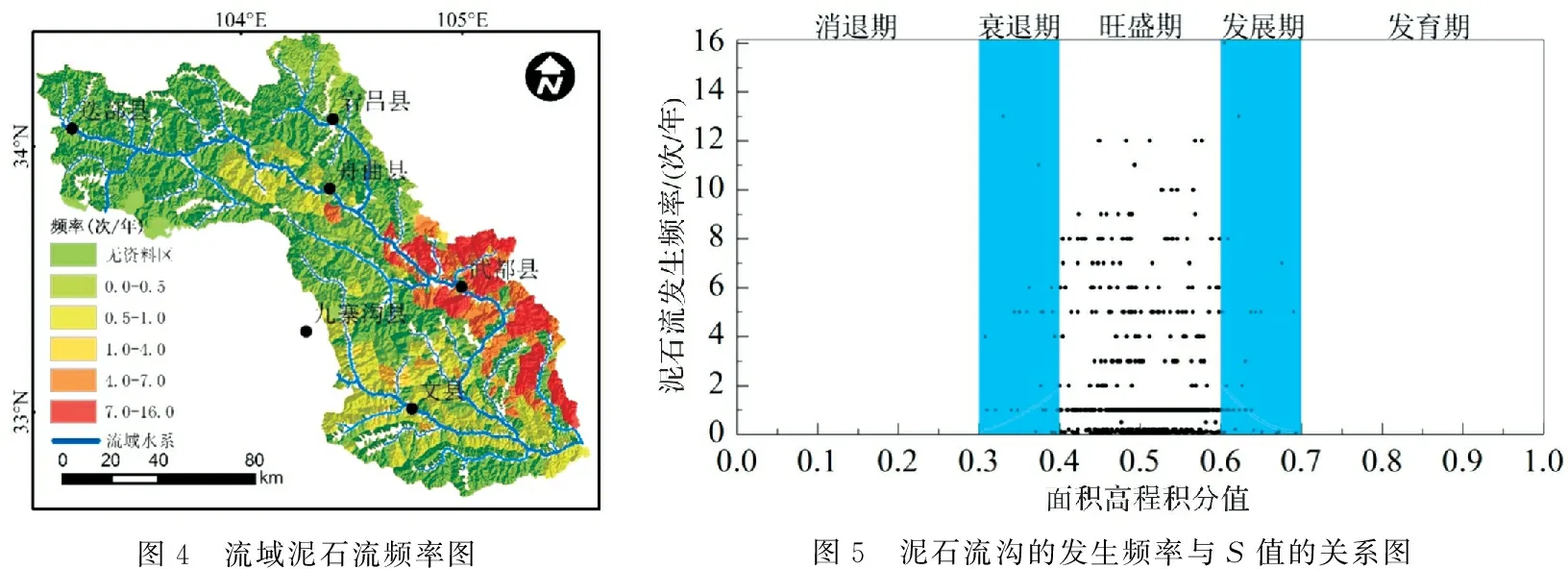
图4 流域泥石流频率图图5 泥石流沟的发生频率与S值的关系图

表3 泥石流发育阶段划分及其对应泥石流发育特征

白龙江内所有沟的S值范围为0.15～0.8，有泥石流记录的沟的S值范围为0.3～0.7，且92%的沟S值集中在0.35～0.6之间，这也和地貌演化阶段的壮年期相吻合，说明泥石流作为地貌演化中的一个过程是遵循地貌演化规律的，且发育状态也和地貌演化状态有着较好的一致性。泥石流沟相对较少的S的值域为0.3～0.4和0.6～0.7之间，据这几个特征值我们将其划分了五个发育阶段，这五个阶段及其对应泥石流发育特征总结如表3所示。

4 结论

本文总结了侵蚀流域系统的地貌信息熵与超熵的应用现状，通过分析地貌信息熵与超熵理论来源，认为这些应用的根本依据是其能够反映泥石流沟的发育阶段。通过S和N的计算方法以及其实际意义的分析认为使用S来对泥石流发育阶段进行定量的划分是比较便捷和可靠。通过泥石流发育频率与S值的统计关系，初步将泥石流的发育阶段划分为发育期、发展期、旺盛期、衰减期和消退期五个阶段，并分析了各个阶段对应泥石流的发育特征。

本文对泥石流的发育阶段的研究只是一个初步的研究，但从一定程度上抓住了泥石流沟演化的一些规律，并在以后的研究中会逐渐深入和优化。泥石流的发育阶段的定量化研究以及各个发育阶段的泥石流特征的分析，能为泥石流在各个发育阶段的防治对策提供理论支持，同时也对潜在泥石流的判定、泥石流危险性评价以及泥石流发生频率的深入分析等研究提供支持。