基于层次分析法的列车折返能力影响因素分析

2018-10-09张帅，杜雯

铁路计算机应用 2018年9期

关键词：道岔排序一致性

张帅，杜雯

（西南交通大学信息科学与技术学院，成都 611756）

近年来，城市前期折返站的设计以及后期的折返站优化设计需综合考虑多种因素。

层次分析法起源于20世纪70年代的美国著名运筹学专家T.L.Saaty[1]。它将与决策有关的元素分解成了目标、准则、方案等层次，通过定性分析与定量计算相结合的方式，将各因素两两比较综合打分，对系统进行整体的评价分析[2]。

因此，笔者根据有关文献确定折返能力影响因素，利用层次分析法确定各影响因素的权重，为前期折返站的设计以及后期折返能力的优化设计提供参考依据。

1 层次分析法基本原理

层次分析法将所要进行决策问题置于一个大的系统中，这个系统中存在相互影响的多种要素，经过分析将其拆分为几个方案或者准则，通过比较将其分为几个层次，从而形成一个多层次的结构模型[3]。它将定性分析和定量分析综合起来，通过层层排序，使得结果简单明确，增加了决策的有效性。采用层次分析法主要包括以下步骤。

1.1 递阶层次构造

通过对折返能力影响因素的分析，后期仅对固定站型做比较分析。将问题分解为几个组成因素，并根据因素之间的联系以及属性分为不同的层次，其中，层次可分为：确定评价的总目标层（M），决定总目标的准则层（B），以及影响因素的指标层（C）[4]。建立此模型的目的是为了确定折返因素的权重，并根据求得的结果进行优化分析。准则层（B）是从速度、经济、可实施性以及合理性4个方面来决策折返能力的优化方向，然后通过分析各折返能力影响因素与准则层的相关性列入指标层。

1.2 比较判断矩阵构造

当我们构造层次模型之后，通过两两因素作对比，对照相应的评价尺度，如表1所示。按相对重要性对每个因素做出定量的判断，通过量化构造每个层次的判断矩阵。

表1 相对重要性标度含义

针对同一个层次的各指标专家进行两两比较并打分，当对所有的指标进行判定之后，便构造一个比较判断矩阵P。

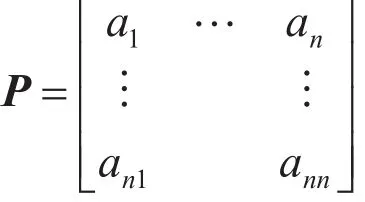
式中，aij为元素i与j的重要性。

1.3 权重向量计算

根据构造所得的判断矩阵，求出该矩阵的最大特征根λmax以及特征向量ω。

对判断矩阵P每一行的元素求几何平均值：

式中，n为矩阵的阶数。

所求特征向量ω经归一化处理：

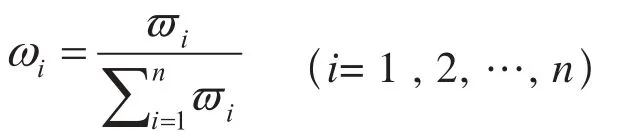
式中，ωi为所求指标的权重系数值，最后的权重向量为：W=(ω1, ω2,…, ωn)T。

1.4 一致性检验

权重分配是否合理，还需要对判断矩阵进行一致性检验，若不合理，还需做进一步的修改。

定义一致性指标为：

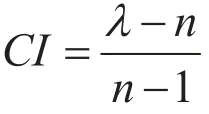
其中，n为矩阵的阶数；λ为最大特征值。

定义随机一致性指标为RI,其数值，如表2所示。

表2 随机一致性指标的值

定义一致性比率为：

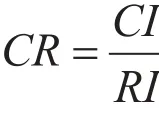
当CR＜0.1时，则该判断矩阵的不一致程度在可允许的范围内，能够使用计算所得的归一化特征向量作为权向量。否则需要重新构造判断矩阵。

2 城市轨道交通折返能力影响因素

2.1 折返站型对折返能力的影响

不同的折返站型具有不同的折返方式，折返站型分为站前折返、站后折返以及混合折返[5]，不同的折返站型具有不同的折返能力，城市轨道交通折返站的不同，会直接影响到折返站的折返能力以及相应渡线的设置方式。所以在前期的设计过程中应该考虑多方面因素，满足后期的客运需求。

2.2 折返方式对折返能力的影响

在折返过程中，可将折返方式归结为单一直进弯出折返、单一弯进直出折返以及交替折返，不同的折返形式对于折返能力影响也很大，计算折返能力选取的是最大的折返时间间隔。但是折返站型一旦固定，后期优化站型需要造价高同时也不易于实施，所以采用何种折返方式也是后期优化的一个研究方向。

2.3 站前限速对折返能力的影响

列车折返间隔时间有以下几种表现形式，接车间隔时间、发车间隔时间和出发间隔时间[6]。其中站前限速会直接影响到接车间隔时间，站前限速值的大小以及站前限速点的位置，会影响到制动距离的长短和运行时间，从而间接影响到折返时间的大小，但是限速值的确定也会影响到列车的能耗问题，所以后期站前限速点的确定以及站前限速值的研究也是优化的一个研究方向。

2.4 道岔类型对折返能力的影响

道岔在折返作业中是一个重要的设备，道岔的类型直接影响到道岔限速，在折返过程中，列车经由道岔侧向来完成整个折返过程，所以道岔的类型以及道岔限速对折返能力有着重大的影响。道岔型号越大那么道岔限速值会越高，但是会影响到折返走行距离以及造价，所以选用何种道岔需要仔细考虑。

2.5 停站时间对折返能力的影响

车站的停站时间占折返间隔时间中的40%，它主要跟车站的客流量、列车的编组、以及车门的宽度等因素有关[7]，所以停站时间的缩短也会减少折返间隔。但停站时间的修改必须在合理的范围内。

2.6 折返走行距离对折返能力的影响

折返走行距离直接关系到列车折返能力的大小，它主要受到线间距以及站台长度的影响，站台的长度由列车编组方案确定，列车长度越长，出清车站的时间就会越长，对后续列车的追踪间隔也就会越大[8]。而线间距的影响主要是影响侧线的长度，所以前期考虑列车编组以及线间距会直接影响到折返走行距离，从而影响到折返能力。

3 构建层次模型

3.1 城市轨道交通折返能力影响因素权重模型的建立

根据以上分析得出，城市轨道交通折返能力影响因素权重模型，如图1所示。

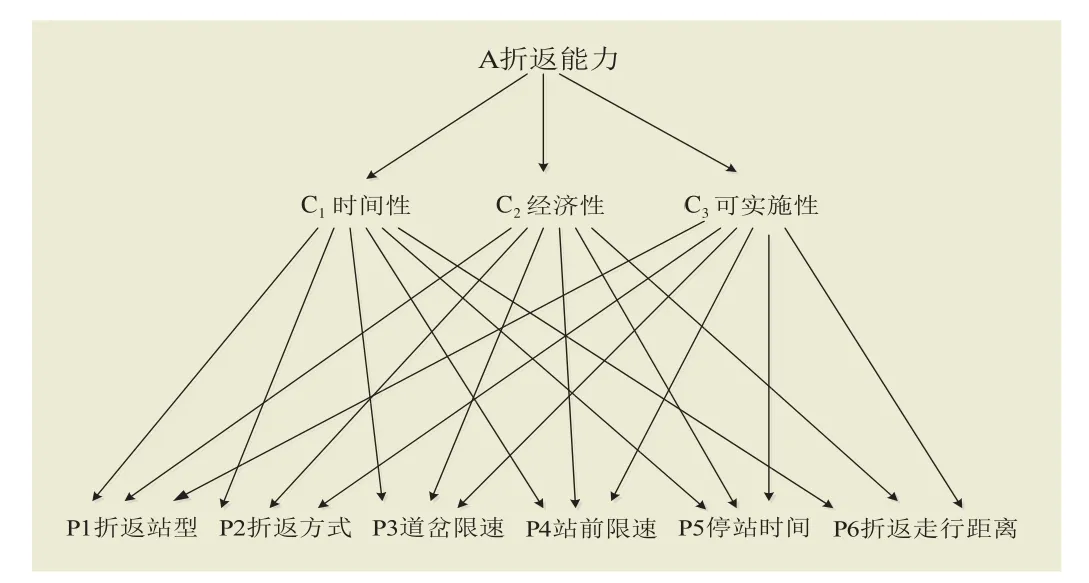
图1 城市轨道交通折返能力影响因素权重模型

3.2 各因素的权重计算及一致性检验

建立A-C的判断矩阵，准则层主要由3个因素构成，即C1时间性、C2经济性、C3可实施性，两两比较赋值，构造矩阵A3×3。

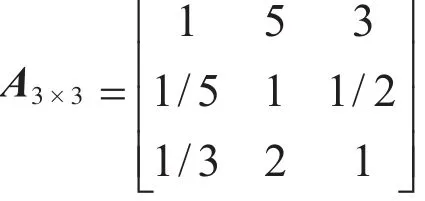
经计算可得矩阵A的最大特征根为λ=3.004，对应的特征向量为：

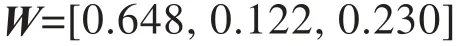
进行一致性检验得：

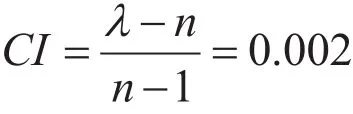
当n=3, RI=0.58时，一致性比率为：

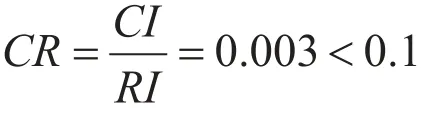
通过检验。

再构造方案层对准则层的判断矩阵，方案层主要由6个因素构成，即P1折返站型、P2折返方式、P3道岔限速、P4站前限速、P5停站时间、P6折返走行距离，两两因素进行比较，按相对重要性对每个因素做出定量的判断，通过量化构造矩阵C6×6。

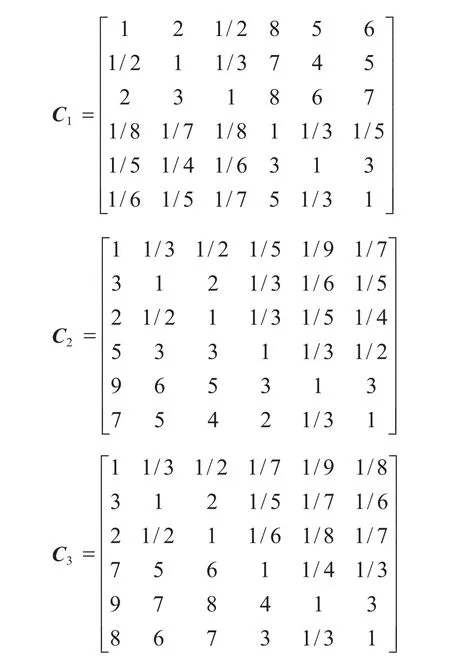
经计算可得Ci矩阵的特征向量Wi=[Wi1, Wi2, Wi3,Wi4, Wi5, Wi6]，通过式 CI=(λ-n)/(n–1)、CR=CI/RI可分别得到矩阵Ci的一致性指标CI和一致性比率CR，其中，λ为矩阵Ci的最大特征根，RI为表2定义的随机一致性指标，计算结果，如表3所示。

通过表3可知，对WC1～WC3进行一致性检验可得，每个判断矩阵的一致性比率CR的值均＜0.1，说明一致性程度均符合要求。

3.3 层次总排序及一致性检验

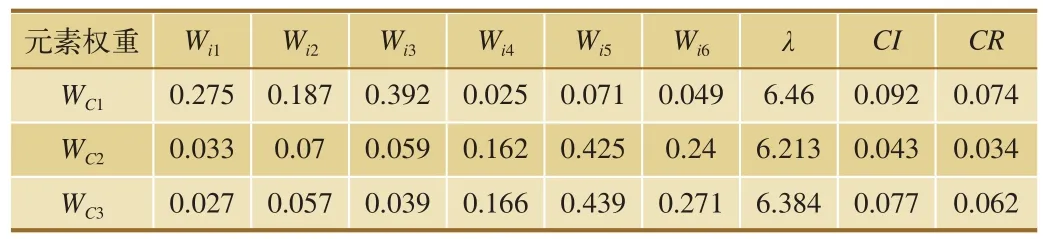
表3 单层判断矩阵计算结果

计算层次中所有因素对于最高层相对重要性的权值，并对权值进行排序，称为层次总排序[9]。

计算某层各因素对应于最高层的权重为WP1,WP2,…, WPi：

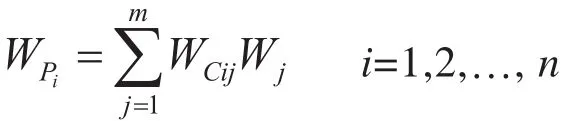
式中，Wj为上一层次m个因素层次总排序的权重；WCij为本层的层析单排序权重。

P层总排序的一致性比例CR由下式计算得出：

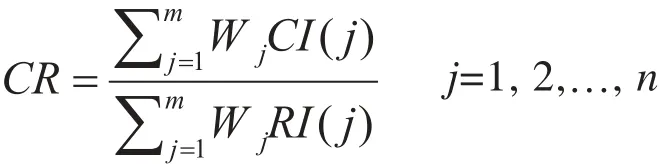
式中，CI(j)为已计算得出的本层一致性指标，RI(j)为平均随机一致性指标。

通过上式计算可得：CI=0.083， RI=1.24。可计算得 CR=0.067＜0.1，层次总排序通过一致性检验。

Ci各因素对应于目标层的权重为：

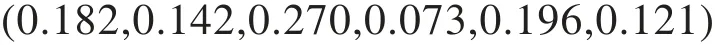
4 优化设计

从计算结果可知，按时间性为最大准则来看，道岔限速是最大的影响因素，其次是站型设计，但站型确定后，后期不易修改，所以在设计初期需选用合适的折返站型。对于道岔限速，针对现有道岔类型，可通过提高道岔侧向行驶速度提高折返能力。在站型、道岔类型确定后，后期如果要提高折返能力，从经济性、可实施性来说都是很难的，所以可通过压缩站停时间以及改变折返方式从而压缩折返时间，进而提高折返能力。