BeiDou+GLONASS+Galileo多系统组合SPP稳定性和精度分析
2018-10-09布金伟左小清金立新李海强周羽佳
布金伟,左小清,金立新,李海强,周羽佳,常 军
(1. 昆明理工大学国土资源工程学院,云南 昆明 650093; 2. 中铁第一勘察设计院集团有限公司,陕西 西安 710043; 3. 甘肃铁道综合工程勘察院有限公司,甘肃 兰州 730000; 4. 国家测绘地理信息局第一大地测量队,陕西 西安 710054)
伪距单点定位具有定位速度快且不存在整周模糊度问题,原理简单易于编程实现等优点。目前,一些学者对GPS+BeiDou、GPS+GLONASS、GPS+Galileo、GPS+GLONASS+Galileo和GPS+GLONASS+BeiDou多系统组合伪距单点定位进行了相关的研究[1-5],研究表明:多系统组合伪距单点定位可以提高定位的稳定性和精度[6-8]。
然而,对于BeiDou+GLONASS+Galileo多系统组合SPP的研究相对较少。因此,我国BDS对多系统组合SPP解算性能的贡献有待进一步研究。鉴于此,本文在现有研究的基础上,分析BeiDou+GLONASS+Galileo之间的时间和坐标系统差异,并推导了BeiDou+GLONASS+Galileo多系统组合SPP的数学模型;然后从可见卫星数、DOP值、不同高度角下定位性能和定位精度几个方面分析其不同组合模式下(单系统:BeiDou、GLONASS、Galileo;双系统:BeiDou+GLONASS、BeiDou+Galileo、GLONASS+Galileo;三系统:BeiDou+GLONASS+Galileo)的SPP解算性能,最终得出有益结论。
1 BeiDou+GLONASS+Galileo多系统组合SPP基础理论
1.1 时间基准和坐标基准的统一
为解算测站的坐标,必须首先实现BeiDou+GLONASS+Galileo三系统的时间系统和坐标系统的统一。文献[9]和文献[10]指出:BeiDou时间基准采用BDST,GLONASS时间基准采用GLONASST,Galileo时间基准采用GST。对于3个系统时间基准之间的差异和联系,文献[11]已经给出比较详细的叙述和转换公式,这里不再阐述。
文献[12—14]指出,BeiDou坐标基准采用CGCS2000坐标系,GLONASS坐标基准采用PZ-90坐标系,Galileo坐标基准采用GTRF坐标系。鉴于WGS-84坐标系目前已经较为成熟且被广泛使用,本文考虑将各框架按照赫尔墨特变换模型解算出的转换参数统一至WGS-84坐标系下。在满足精度的前提下,CGCS2000、WGS-84和GTRF坐标系统的差异较小,三者之间的差异为cm级。对于单点定位而言,其定位精度在m级,因此在数据处理过程中,可不考虑三者坐标系统差异引起的结果偏差。而PZ-90与WGS-84坐标系的差异能够达到20 m[11],故需考虑PZ-90和WGS-84坐标之间的转换,目前世界公认精度最高的转换参数为俄罗斯飞行控制中心(Russian Mission Control Center,RMCC)利用全球激光跟踪站测算得到的转换参数[9,11]。
1.2 BeiDou+GLONASS+Galileo多系统组合SPP定位模型
在多系统组合定位时,在某历元t可以同时观测到多个系统的卫星信号,因此对于BeiDou+GLONASS+Galileo组合SPP的观测方程可表示为[15]
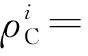
(1)
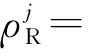
(2)

(3)
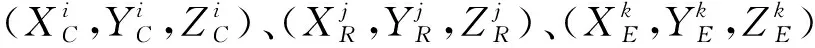
在观测方程式(1)—式(3)的基础上,设测站近似坐标为(x0,y0,z0),并记δx=x-x0,δy=y-y0,δz=z-z0,然后在(x0,y0,z0)处用泰勒级数展开,可得到误差方程

(4)
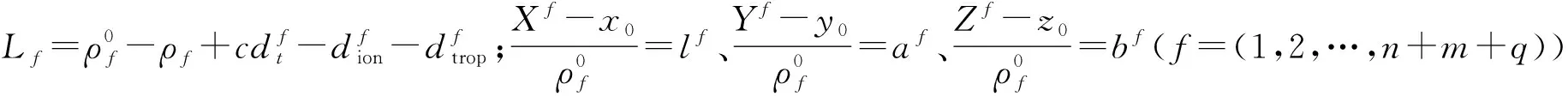
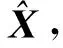
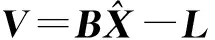
(5)
三系统组合伪距单点定位待估参数中含有3个坐标分量参数和3个接收机钟差,当观测的卫星数大于伪距定位的待估参数个数时,可采用最小二乘法原理求解,此时必要观测卫星数为6颗。由最小二乘估计可得
(6)
式中,P为观测值权阵。
从而求出测站的坐标为
[xyz]T=[x0y0z0]T+[δxδyδz]T
2 试验分析
为了分析BeiDou+GLONASS+Galileo组合伪距单点定位解算性能,试验数据选取MGEX跟踪站的部分测站2016年9月6日和10月25日共2 d的观测数据,数据采样率为30 s。试验方案采用:单系统(BeiDou、GLONASS、Galileo,简写为C、R、E)、双系统(BeiDou+GLONASS、BeiDou+Galileo、GLONASS+Galileo,简写为CR、CE、RE)与三系统(BeiDou+GLONASS+Galileo,简写为CRE)组合共7种定位模式。
2.1 卫星可见数和DOP值分析
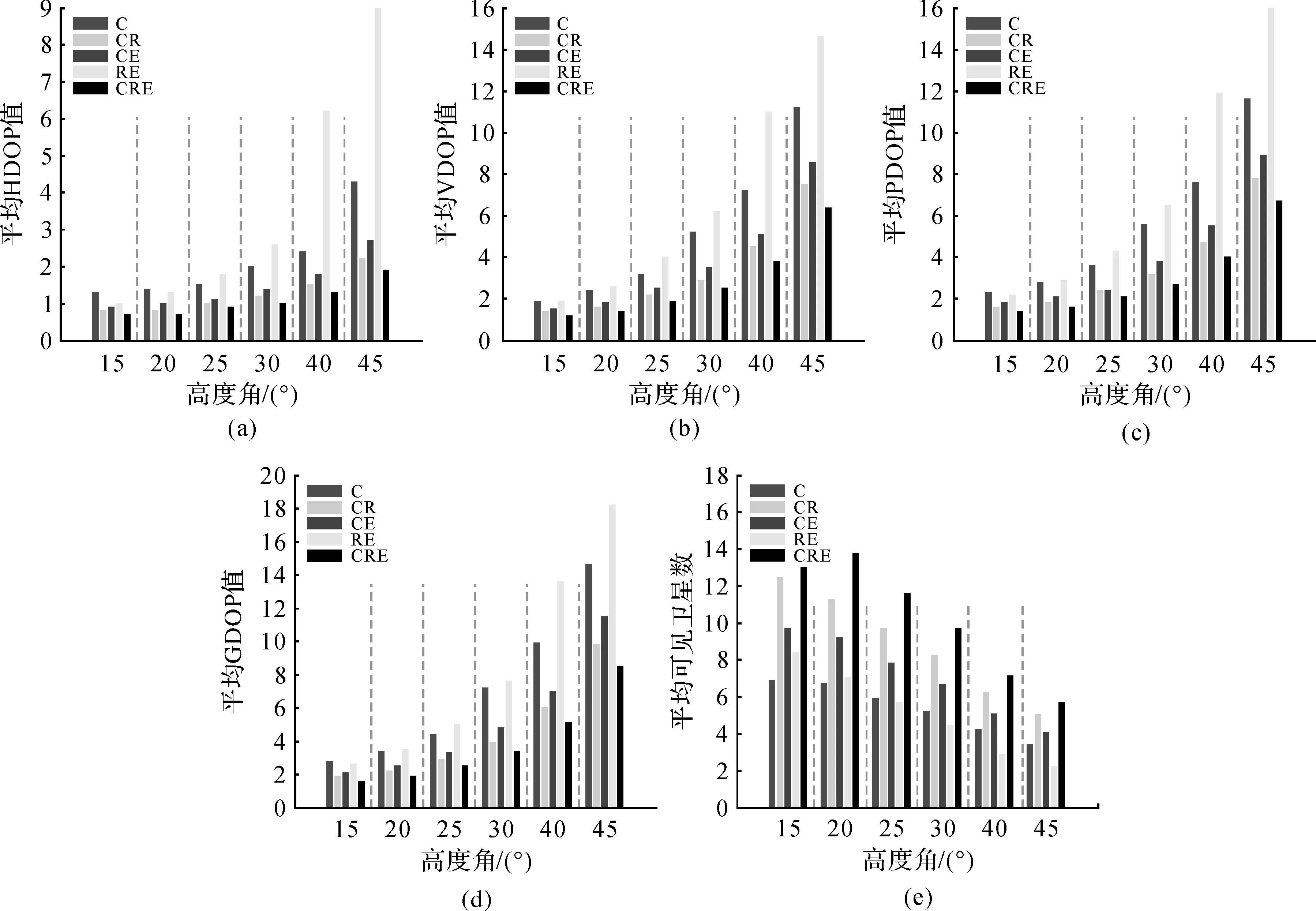
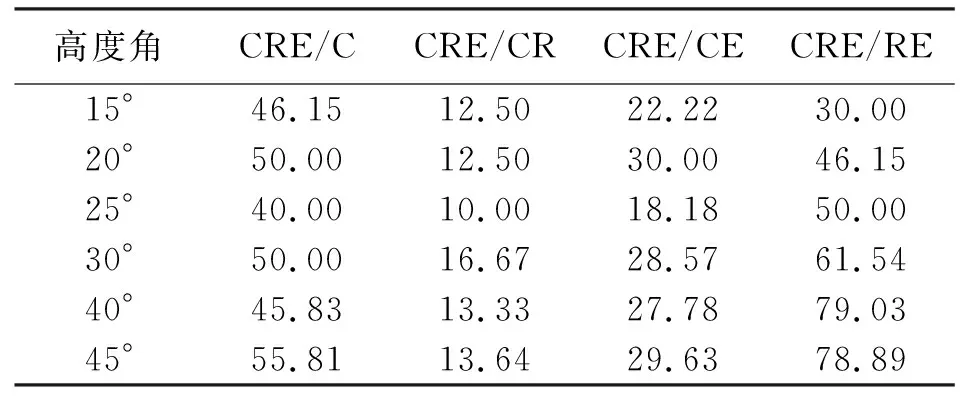
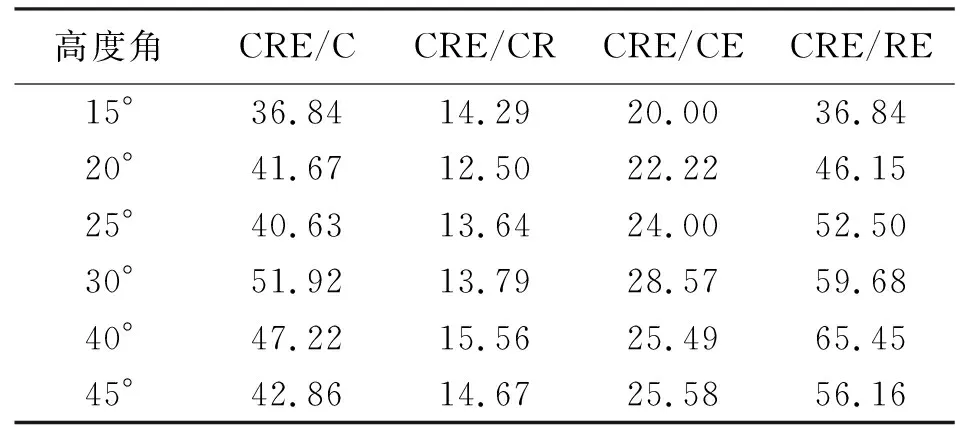
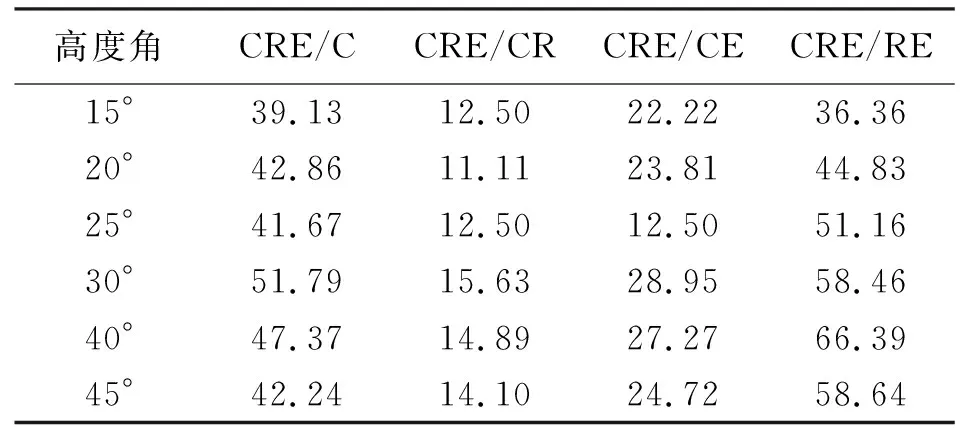
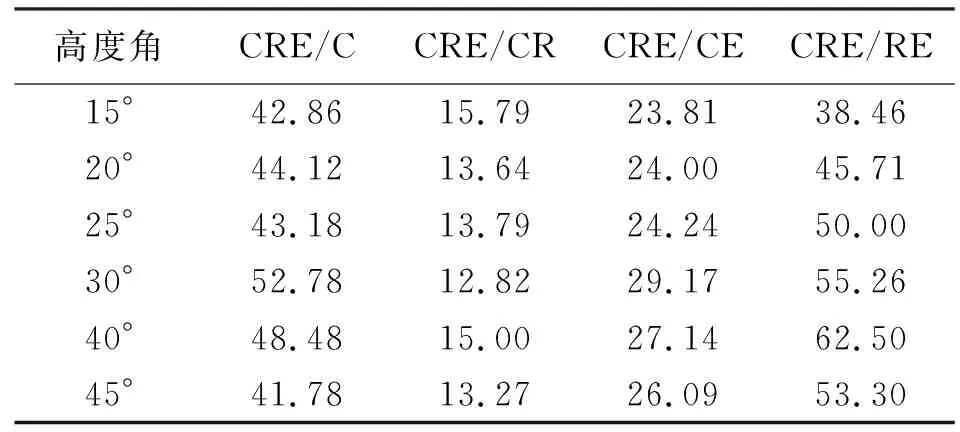
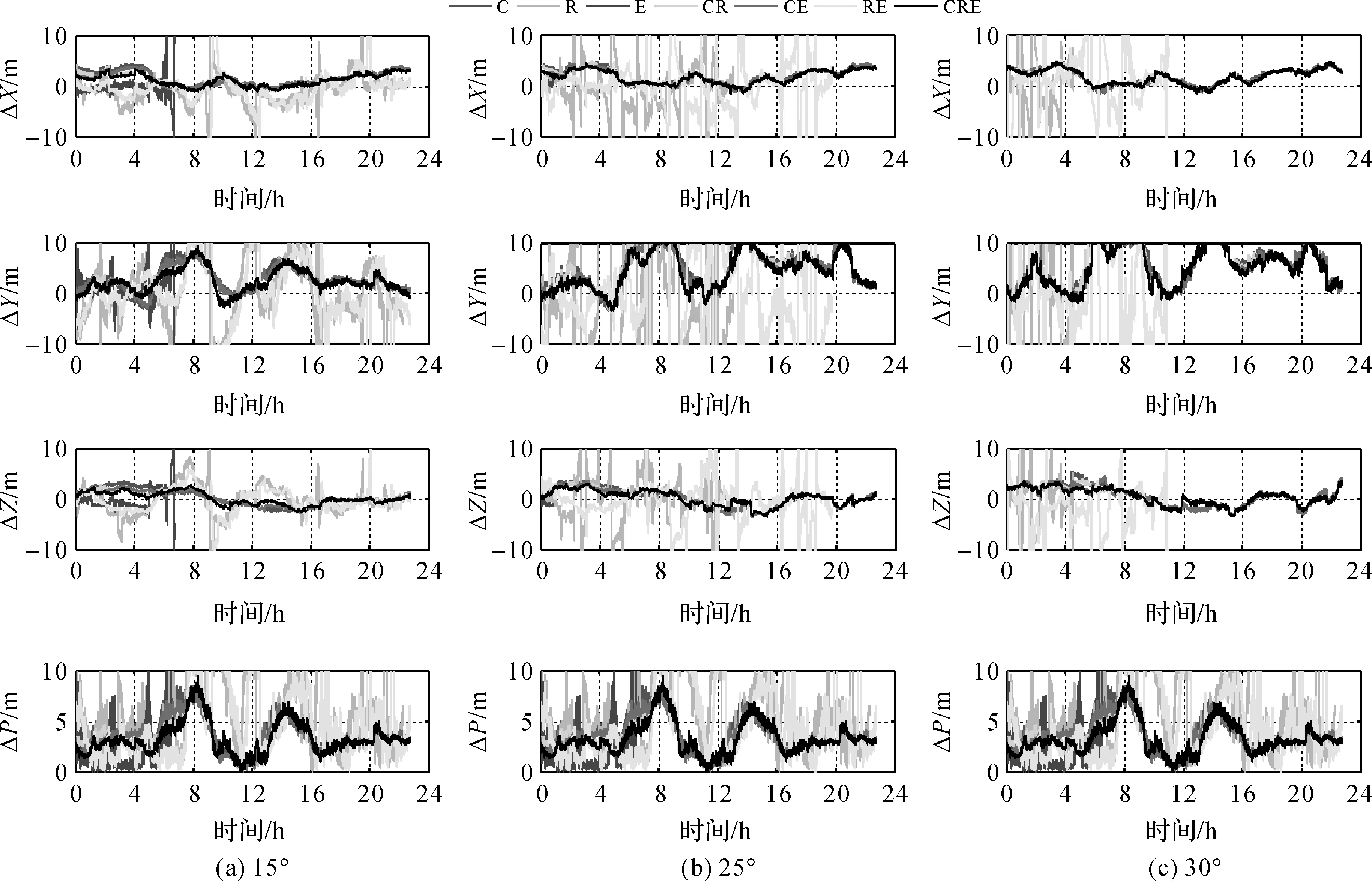
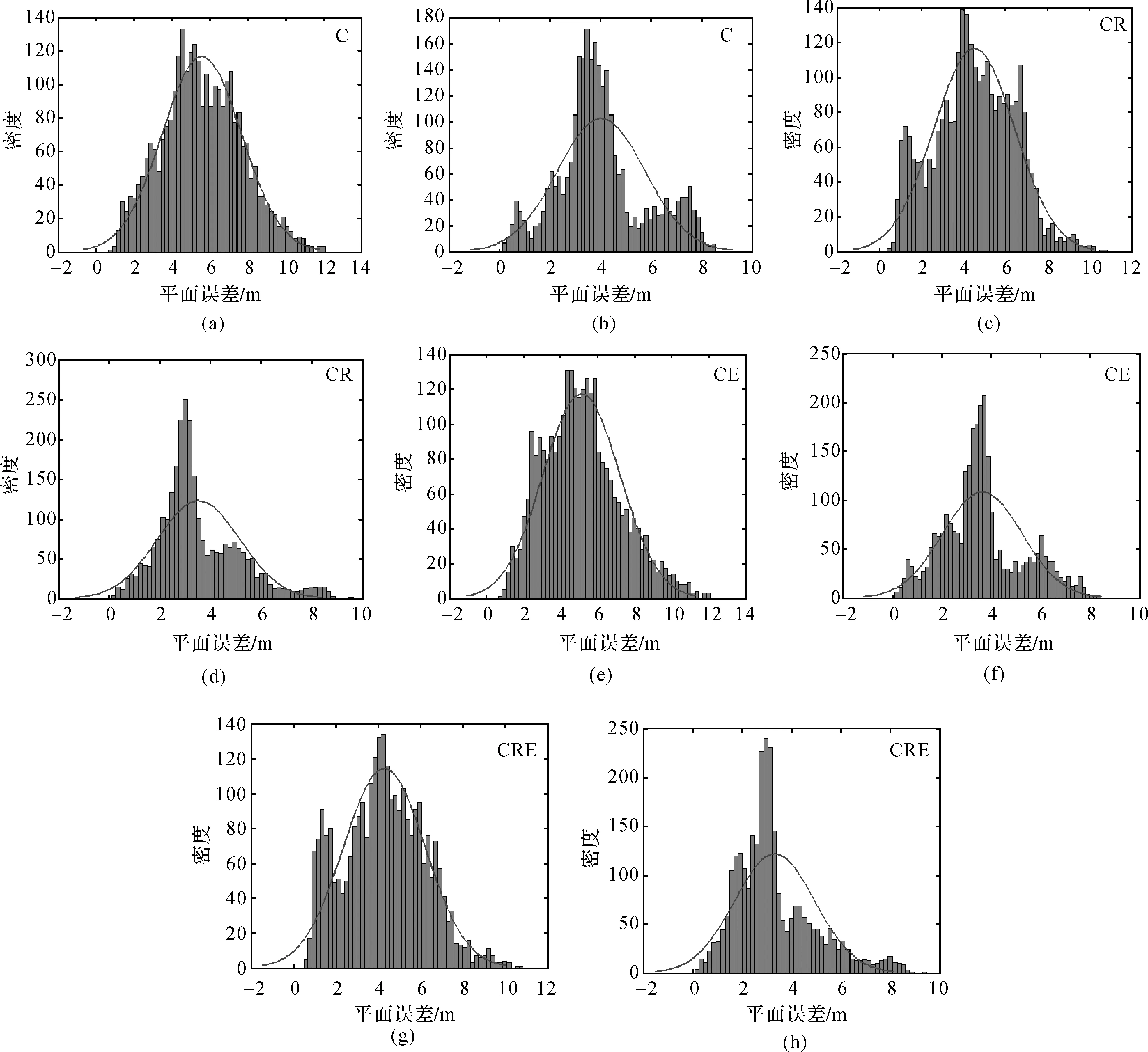
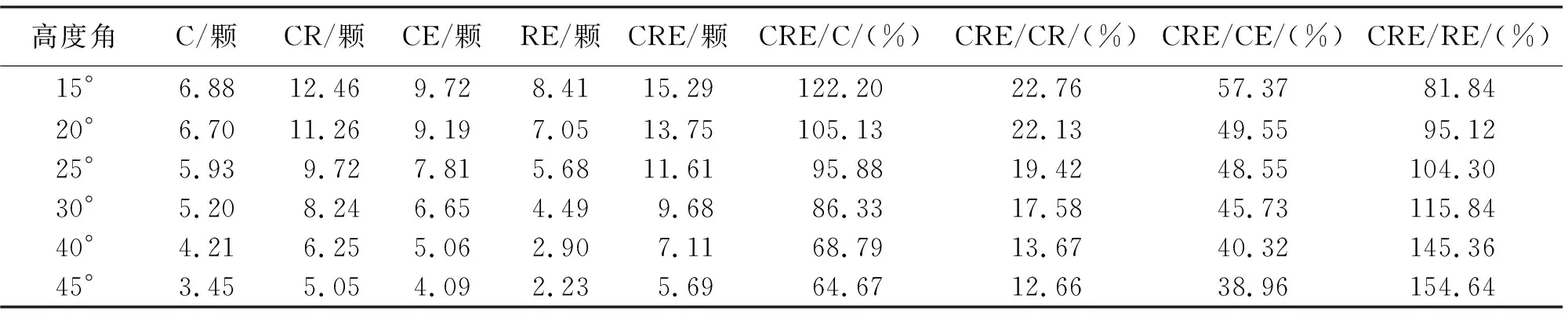
为分析BeiDou+GLONASS+Galileo组合的卫星可见数和DOP值,本文选取测站ANMG进行试验,图1给出了BeiDou+GLONASS+Galileo组合在不同截止高度角(高度角分别设为15°、30°、40°)下的卫星可见数和DOP值比较。图2给出了1 d内BeiDou+GLONASS+Galileo组合模式在不同截止高度角情况下的平均DOP值和平均可见卫星数统计。从图1和图2可知,当截止高度角为15°时,1 d内BeiDou+GLONASS+Galileo三系统组合可见卫星数均在10颗以上,平均可见卫星数在14颗左右。DOP值较小且波动平缓稳定,平均DOP值小于2,说明卫星的空间几何结构分布较好;当截止高度角为30°时,BeiDou+GLONASS+Galileo三系统组合卫星可用性仍然较高,全天内平均可见卫星数为9.68颗。平均HDOP、VDOP、PDOP、GDOP值均小于5,而此时在1 d 内大约有2 h DOP值波动较大;当截止高度角大于40°时,所有组合模式的DOP值波动都较大,相比较而言,BeiDou+GLONASS+Galileo三系统组合全天内DOP波动情况比其他组合模式稍好,主要是由于三系统组合在任何时间段内可见卫星数都多于其他组合模式,提高了卫星的可用性和可靠性。结合图2 (e)分析可知,7种定位模式下,从1 d内能观测卫星的时间和卫星数来看可以得出关系:BeiDou+GLONASS+Galileo>BeiDou+GLONASS>BeiDou+Galileo>BeiDou>GLONASS+Galileo>GLONASS>Galileo。由于文中所选的测站在观测1 d内GLONASS和Galileo可见卫星数较少,无法获得可靠的DOP值,故针对BeiDou、BeiDou+GLONASS、BeiDou+Galileo、GLONASS+Galileo、BeiDou+GLONASS+Galileo 5种模式可以得出DOP值大小比较关系:BeiDou+GLONASS+Galileo 图1 多种组合模式在不同截止高度角下的卫星可见数和DOP值比较 图2 平均DOP值和平均可见卫星数 为了分析BeiDou+GLONASS+Galileo三系统组合的DOP值和可见卫星数相比其他组合模式的改善情况,表1—表5分别给出了CRE组合较其他模式的DOP值改善统计结果和可见卫星数增加百分比统计。由表1—表4可知,当截止高度角小于30°时,HDOP、VDOP、PDOP、GDOP三系统组合较其他组合模式分别改善10%~61%、12%~59%、11%~58%、13%~55%;当截止高度角为40°时,CRE三系统组合的HDOP、VDOP、PDOP、GDOP较CR和CE组合分别改善13.33%和27.78%、15.56%和25.49%、14.89%和27.27%、15.00%和27.14%;较C和RE组合改善率均大于45%;当截止高度角为45°时,CRE三系统组合的HDOP和VDOP较C组合分别改善55.81%和42.86%,CRE三系统组合垂直方向上的改善效果稍差于水平方向。由表5可知,无论何种情况的截止高度角,CRE三系统组合的可见卫星数都多于单系统和双系统组合,特别是在截止高度角大于30°时,全天内的可见卫星数能保持在6颗以上,提高了定位的可靠性和稳定性。 图3给出了测站GMSD在单系统、双系统和三系统7种模式下单点定位结果(X、Y、Z方向的偏差为DX、DY、DZ,点位偏差为DP,图3(a)截止高度角为15°,图3(b)截止高度角为25°,图3(c)截止高度角为30°)。从图3可以看出:①对于同一种定位模式,随着高度角的增加,定位稳定性有所降低;②在不同截止高度角下,BeiDou+GLONASS+Galileo三系统组合单点定位稳定性都最优,尽管截止高度角增加时(30°时),X、Z方向的偏差和点位偏差均小于10 m,Y方向的偏差小于12 m,点位偏差小于10 m。 表1 HDOP值改善统计结果 (%) 表2 VDOP值改善统计结果 (%) 表3 PDOP值改善统计结果 (%) 表4 GDOP值改善统计结果 (%) 为分析单系统(C)、双系统(CR、CE)和三系统(CRE)4种模式单点定位的定位精度情况,图4分别给出了1 d内2个测站(其中图4(a)、(c)、(e)、(g)为GMSD测站统计结果,图4(b)、(d)、(f)、(h)为ANMG测站统计结果)不同模式的单点定位精度直方图。如图4所示,横轴表示定位的平面误差,纵轴表示分布密度,图中的曲线为密度曲线,从图中可以明显看出,对于单系统而言,GMSD测站BeiDou系统(如图4(a)所示)的平面定位精度为12 m,并且定位精度主要分布在0~12 m范围内,密度曲线的波峰位于3~7 m范围内,ANMG测站BeiDou系统(如图4(b)所示)的平面定位精度为8 m,定位精度主要分布在0~8 m范围内,密度曲线的波峰位于2~5 m范围内;对于双系统而言,GMSD测站CR、CE组合系统(如图4(c)、(e)所示)的平面定位精度分别为10 m、12 m,定位精度分别主要分布在0~10 m、1~12 m范围内,密度曲线的波峰分别位于3~6 m、3~7 m范围内,ANMG测站CR、CE组合系统(如图4(d)、(f)所示)的平面定位精度分别为8 m、8 m,定位精度分别主要分布在0~8 m、0~8 m范围内,密度曲线的波峰分别位于2~5 m、2~4 m范围内;然而对于三系统而言,GMSD测站CRE系统(如图4(g)所示)的平面定位精度为10 m,平面定位精度主要分布在0~8 m范围内,密度曲线的波峰位于3~5 m范围内,ANMG测站CRE系统(如图4(h)所示)的平面定位精度为8 m,定位精度主要分布在0~8 m,密度曲线的波峰位于2~4 m范围内;通过以上2个测站的分析,相比单系统和双系统组合模式,三系统组合定位在1 d内的定位精度优于10 m,定位精度较高且定位结果相对集中。 图3 多种组合模式单点定位结果在X、Y、Z方向的偏差和点位偏差 图4 1 d内4种模式单点定位精度直方图 高度角C/颗CR/颗CE/颗RE/颗CRE/颗CRE/C/(%)CRE/CR/(%)CRE/CE/(%)CRE/RE/(%)15°6.8812.469.728.4115.29122.2022.7657.3781.8420°6.7011.269.197.0513.75105.1322.1349.5595.1225°5.939.727.815.6811.6195.8819.4248.55104.3030°5.208.246.654.499.6886.3317.5845.73115.8440°4.216.255.062.907.1168.7913.6740.32145.3645°3.455.054.092.235.6964.6712.6638.96154.64 本文通过对单系统(C、R、E)、双系统(CR、CE、RE)与三系统(CRE)共7种定位模式进行单点定位解算和结果分析,得出如下结论: (1) 针对文中所选的测站而言,当高度角达到40°时,在可见卫星数方面,无论单系统、双系统还是三系统组合可见卫星数均小于10颗,1 d内大部分时间都无法观测到卫星,而BeiDou+GLONASS+Galileo三系统组合大于18 h能观测平均6颗以上,BeiDou+GLONASS双系统组合次之;在DOP值方面,CRE三系统组合的HDOP、VDOP、PDOP、GDOP较其他组合模式改善大约13%~45%,1 d内DOP值变化较其他组合模式波动小。 (2) 单系统模式中BDS系统定位稳定性最优,Galileo系统最差,双系统模式中BeiDou+GLONASS、BeiDou+Galileo组合系统定位稳定性最优,GLONASS+Galileo系统最差,而BeiDou+GLONASS+Galileo组合系统定位稳定性优于其他6种模式。 (3) 从定位精度来看,相比单系统和双系统组合模式,BeiDou+GLONASS+Galileo三系统组合定位在1 d内的定位精度较优且定位结果相对集中。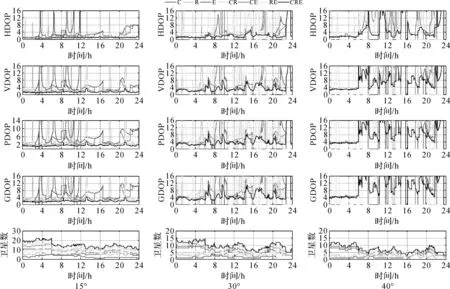
2.2 不同高度角下定位稳定性分析
2.3 定位精度分析
3 结 论
