一类SIRS传染病模型的稳定性

吴长青, 黄勇庆, 朱长荣

( 1. 重庆大学 数学与统计学院, 重庆 401331; 2. 重庆育才中学, 重庆 400050; 3. 重庆第一中学, 重庆 400030)

传染病常常严重地影响着人们正常的日常生活,比如，流行感冒、天花，以及令人印象深刻的2008年的非典和现在依然流行的艾滋病,它们都是典型的可传播疾病.由于可传播疾病的厉害性，促使人们不断去研究传染病的传播规律.于是这就涉及到包括医学、数学、人文、地理等学科在内的传染病.而在数学上建立正确的传染病动力系统模型又是有效地研究传染病的重要一环.人们期待着从传染病动力系统模型的研究中去找到传染病的流行规律，进而有效地预防和阻止传染病的产生与传播；减少对人类生命的威胁和财产的损失.

从Kermack等[1]研究1665-1666伦敦瘟疫开始，从数学的角度去研究传染病的传播规律就成为了研究和控制传染病的重要工具.之后，研究传染病模型的动力行为就成为了一个热门课题.经典的Kermack-Mckendrick模型是以仓室为单位，把人群分为3个仓室建立起的仓室模型，这3个仓室分别是带有传染病人群中的易感染者S、感染者I、移出者R.根据不同的仓室，又可以建立起相应的模型，其中主要包括了SIR[2]、SIS[3]、SIRS[4]和SEIRS[5]等模型.在这些动力系统模型当中有一个非常重要的因素是感染率.对于感染率，文献[6]曾在模型中引入饱和发生率g(I)S[7]，其中g(I)是感染者个体的增加量，g(I)=kI/(1+αI).Liu等[8]研究过更一般的发生率KSIi/(1+αIj)，参数i,j>0和α≥0.Song等[4]研究了发生率为kSI2/(1+βI+αI2)的传染病模型

R′(t)=μI-(d+δ)R,

(1)

其中S(t)、I(t)和R(t)分别对应着t时刻的易感染者、感染者和移出者；b是人口出生率或迁入率；d是人口的自然死亡率；k是一个比例常数；μ是感染类中的自然恢复率；δ是移出类中由于失去免疫能力再次成为易感染者的比率；α是一个正参数；β是一个满足使得对于∀I≥0都有1+βI+αI2>0的正参数.

在考虑传染病模型的时候，人们总要假定在总人口数不变的情况下，来考虑模型发生的动力性态.这将把三维的模型限制在三维空间上的一个超曲面去定性研究系统平衡点的稳定性和分岔.Song等[4]也以此做了类似的研究，它假设S+I+R=N，其中N为常数，在I-R平面内，研究了系统的稳定性和分岔情况.但是在现实生活当中又很难满足总人口不变的理想假设.所以一般而言，N不一定是常数，它总会随着时间的推移而改变.基于此，本文将在总人口为变量的假设下，以Ruan等[9]研究的方法为基础，研究模型(1)的动力性态.

1 平衡点及其动力性态

为了使计算简便，在系统(1)中需要引入一些同胚变换.令

则系统(1)转化为下面等价的系统

z′=qy-z,

(2)

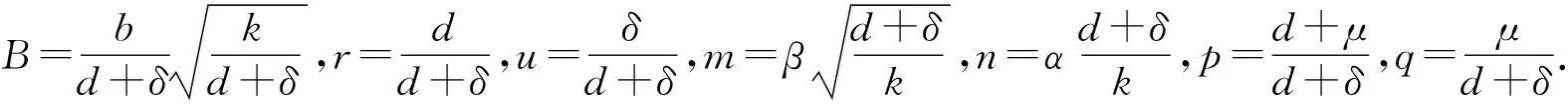
1.1方程(2)的平衡点下面考察系统(2)的平衡点.系统(2)的平衡点是下面代数方程的解：

(3)

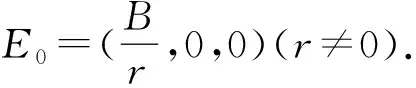
(4)

然后再把方程(4)代入方程组(3)中的第一个方程有

(prn+p-uq)y2-(B-prm)y+rp=0.

(5)

Δ=(B-prm)2-4rp(prn+p-uq).

定理1对于系统(2)中的平衡点，利用根与系数的关系可能出现以下几种情况：

(i) 当Δ<0时，系统(2)只存在平衡点E0；

(ii) 当且仅当Δ=0和B-prm>0时，系统(2)有平衡点E0和唯一正平衡点E*=(x*,y*,z*),其中

(iii) 当且仅当Δ>0和B-prm>0时，系统(2)有平衡点E0和2个正平衡点Ei=(xi,yi,zi)，i=1，2，其中

yi=

i=1，2.

关于正平衡点又称之为地方病平衡点.从系统(1)和(2)当中可以看到，随着出生率、死亡率和移除率的改变会影响到Δ和B-prm的符号，这就可能会造成系统平衡点的个数发生变化.为此，本文将针对这一变化情况加以讨论.

1.2无病平衡点的动力性态首先讨论无病平衡点E0的稳定性，系统(2)在无病平衡点E0处的Jacob矩阵为

直接计算可知,矩阵J0对应的3个负特征根分别为：λ1=-r,λ2=-p,λ3=-1.于是可得下面的结论.

定理2系统(2)的无病平衡点E0是局部渐进稳定的.

如图1,当系统(2)只存在无病平衡点E0=(6.74,0,0)，即参数值为：B=6.2，r=0.92，m=1.6，n=0.4，u=0.08，p=3.2，q=2.28时，图1(a)～(d)分别是系统(2)在此平衡点附近的S(t)、I(t)、R(t)和SIR图像，它是局部渐进稳定的.

1.3地方病平衡点E*的动力性态系统(2)在平衡点E(x,y,z)处所对应的线性化矩阵为

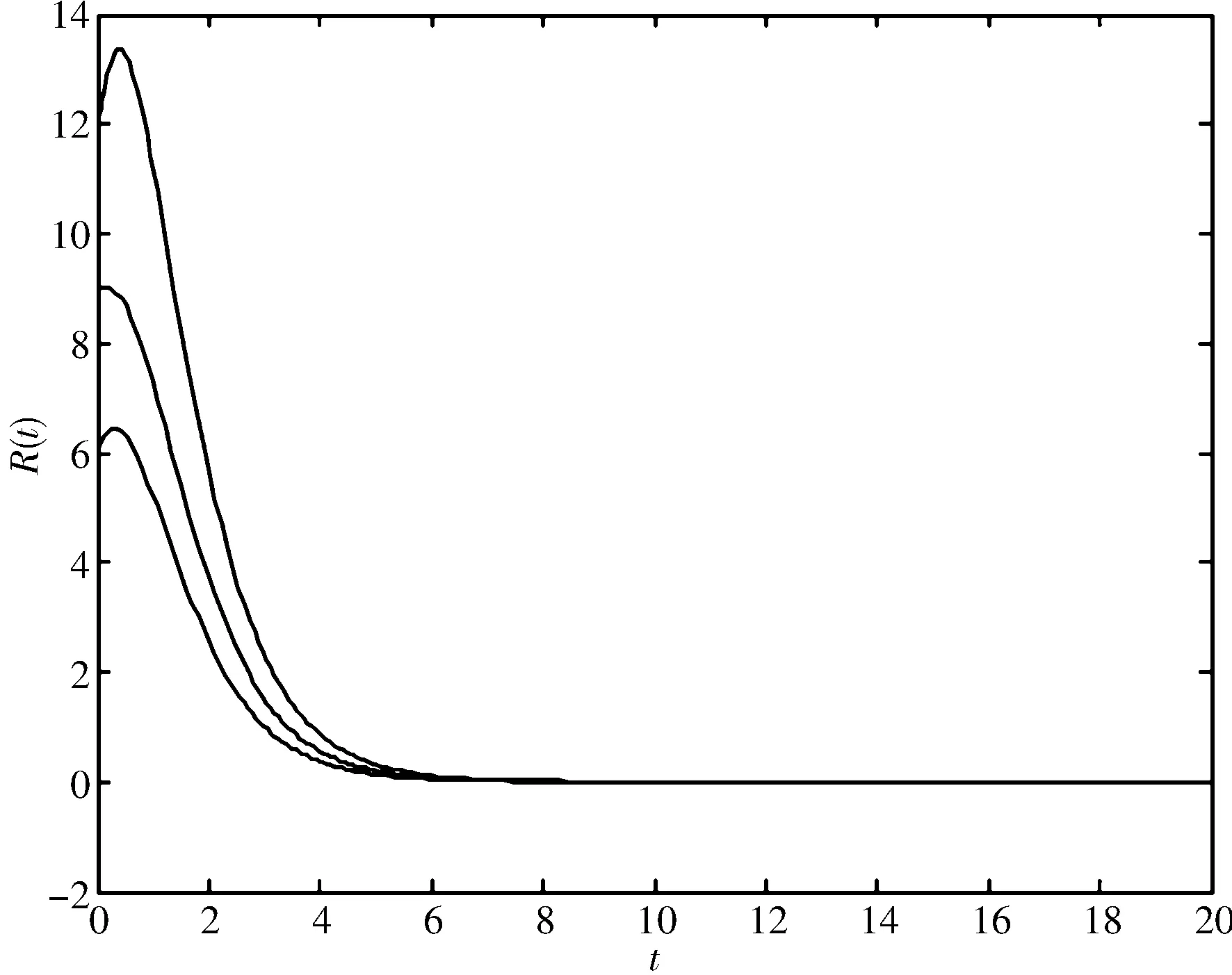
(c) 移除人群的变化趋势 (d) 系统的SIR相图

(6)

其中

矩阵M(E)所对应的行列式为

其符号与下式相反

(7)

矩阵M(E)的迹为

tr(M(E))=

其符号与下式相反

T(y)=(prn+nr+n+1)y2+

m(1+r)y+1+r-p.

(8)

定理3系统(2)的平衡点E*是退化平衡点.

证明当Δ=0时，系统(2)存在平衡点E*.由(7)式计算可知：det(M(E*))=0，所以系统(2)在E*处是退化的.

注1Δ=0，在E*处矩阵(6)对应的行列式det(M(E*))=0，可能出现以下2种情况：

1) 若

(B-prm)2(pn+nr+uq+1)+

2mr(B-prm)(prn+p-uq)+

4(r-p)(prn+p-uq)2≠0,

则系统(2)有一个零特征根.

2) 若

(B-prm)2(pn+nr+uq+1)+

2mr(B-prm)(prn+p-uq)+

4(r-p)(prn+p-uq)2=0,

则系统(2)有2个零特征根.这时系统一般会根据参数的变化发生不同的分岔现象.

如图2,当Δ=0时，系统(2)存在平衡点E0=(2.4,0,0)和E*=(1.20,0.833,0.367)，参数取值为：B=1.334，r=0.56，m=0，n=0，u=0.44，p=1，q=0.44.图2显示的是系统(2)在平衡点E0是局部渐进稳定的，E*的稳定情况将会随着参数的变化而变化.如果Δ<0，相图将转化为图1，如果Δ>0，相图转化为图3.

图 2 Δ=0时系统的SIR相图

1.4地方病平衡点E1的动力性态平衡点E1的稳定性较复杂，它可以是稳定的，也可以是不稳定的，这依赖于不同参数的选取.

定理4当Δ>0时，如果q>1，且有不等式

(pn+nr+n+1)<

m(1+r)](prn+p-uq)

成立，则点E1是系统(2)的不稳定平衡点.

证明由(7)式

可得det(M(E1))>0.同时tr(M(E1))>0.所以E1为系统(2)的不稳定平衡点.

为了判定平衡点E1的稳定性，先引入一个式子

定理5当Δ>0时，如果q≤1，或

(pn+nr+n+1)>

m(1+r)](prn+p-uq)

成立，且存在

Ψ(M(E1))·tr(M(E1))-det(M(E1))<0，

则系统(2)在平衡点E1处是稳定的.

证明根据定理4，平衡点E1处的线性化矩阵对应的行列式det(M(E1))<0.在定理5中的条件成立下，结合(8)式有tr(M(E1))<0.在平衡点E1处计算得

(H+Rn+m2r+2p)y2+m(r+R)y+R,

图 3 Δ>0时系统的SIR相图

其中，H=1+prn+p+pn+nr-uq,R=r-p-pr.由Routh-Hurwitz[10]判定准则，如果满足条件

Ψ(M(E1))tr(M(E1))-det(M(E1))<0，

则平衡点E1是局部渐进稳定的.

如图3,当Δ>0时，系统(2)此时存在无病平衡点E0=(11.4,0,0)，正平衡点E1=(8.14,2.30,0.97)和正平衡点E2=(3.40,5.64,2.37),并且E0和E1是局部稳定的，E2是不稳定的.该图展示的是系统(2)在此种参数情况下的SIR图像；这种情况下的参数取值为：B=8.9，r=0.78，m=1.6，n=0.3，u=0.22，p=1.2，q=0.42.

1.5地方病平衡点E2的动力性态

定理6当Δ>0时，如果系统(2)满足下列条件之一，则地方病平衡点E2是其鞍点：

1)μ≤d+δ;

2)μ>d+δ，

并且

(pn+nr+n+1)>

m(1+r)](prn+p-uq).

证明由(7)式有

不难证明

(B-prm)2+

所以D(y2)<0，则det(M(E2))>0，进而E2是系统的不稳定平衡点.

如果1)成立，则T(y2)>0，即tr(M(E2))<0.

如果2)成立，由于μ>d+δ，则方程T(y)=0有正根

综上所述，如果定理中有一个条件成立，则有tr(M(E2))<0,det(M(E2))>0，所以平衡点E2是其鞍点.

2 数值模拟

下面运用Matlab进行数值模拟，其目的一是通过数值模拟可以进一步验证本文理论的科学性；其二在于，通过图像能更加清晰地表达出系统(2)的解在随其参数变化情况下所反映出的不同情况.下面把本文在数值模拟中所使用到的参数值归类如下：

1)B=6.2，r=0.92，m=1.6，n=0.4，u=0.08，p=3.2，q=2.28.系统(2)只存在无病平衡点E0=(6.74,0,0)，并且局部渐进稳定(图1).

2)B=1.334，r=0.56，m=0，n=0，u=0.44，p=1，q=0.44.系统(2)存在平衡点E0=(2.4,0,0)和平衡点E*=(1.20,0.833,0.367)，并且E0是局部渐进稳定的，E*是不稳定的(图2).

3)B=8.9，r=0.78，m=1.6，n=0.3，u=0.22，p=1.2，q=0.42.系统(2)存在3个平衡点E0=(11.4,0,0)，E1=(8.14,2.30,0.97)和E2=(3.40,5.64,2.37)，其中E0和E1是局部渐进稳定的，而E2则是不稳定的(图3).

3 结束语

本文主要是在带有非线性发生率的传染病模型(1)的基础之上，分析了一个SIRS三维模型的稳定性.对于整个过程，主要分为三步：第一步讨论无病平衡点的局部稳定性；第二步是讨论地方病的局部稳定性；最后是数值模拟验证了本文所有结论的正确性.相比其他文献，本文最大的优点是在没有降低模型维数情况下，讨论了模型的稳定性态，不仅还原了模型本身，也使得结果更加准确.同时也用数学软件很好地验证本篇论文结论的科学性.这是回归模型，回归系统本身，也体现了模型具体的价值.