一类三次微分系统中心存在的条件

唐 璐， 陆征一， 杨 静,2

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066； 2. 中国科学院 成都计算机应用研究所, 四川 成都 610041)

1 预备知识

在常微分方程的定性研究中,中心焦点问题是一个极为重要的课题.最受数学家们关注的是1900年Hilbert提出的著名的2个问题[1],其中第十六问题的后部分就是关于平面自治多项式系统极限环个数的问题,它与中心焦点问题密切相关.实际上,中心焦点问题也是一个困难的、有挑战性的问题,吸引了众多学者关注和研究.

对于一给定的具有线性中心的微分多项式系统：

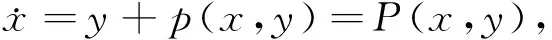
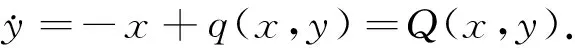
(1)

系统原点为中心的条件一般需要通过计算焦点量得到.计算焦点量主要有Poincare后继函数法及Poincare-Liapunov形式级数法.在计算机代数应用于稳定性理论之前,焦点量的计算是复杂易错的.而后由于计算机代数的发展和应用,越来越多的学者致力于利用计算机计算焦点量.Wang[2]利用Poincare-Liapunov形式级数法得到多项式系统焦点量计算的算法.Gine等[3]给出了一种计算焦点量的递推算法,比较了以往一些焦点量算法的优劣.Lu等[4]给出线性部分非标准形式的多项式微分系统的焦点量的形式级数法的证明和算法.对于二次多项式系统的焦点基,中心条件已由文献[5-7]及随后的一些工作彻底解决.文献[8]通过计算一个三次微分系统前6阶焦点量找出了系统原点为中心的4组必要条件,并利用Darboux积分法和Poincare对称原理验证了必要条件的充分性.桑波[9]利用后继函数法给出焦点量递推公式.文献[10]采用极坐标的形式计算焦点量,得到了形如P(2,2n)的Poincare系统中心的必要条件,利用旋转变换和Poincare对称原理证明了必要条件的充分性.

通过计算焦点量得到的中心条件是必要条件,需要验证这些必要条件的充分性.证明必要条件的充分性一般有2种方法,一种是通过寻找不变代数曲线,构造积分因子,得到多项式系统的首次积分，即若存在函数R∈Ck(U),k≥1使得下列等式成立

(2)

近年来借助计算机代数系统,关于系统化求首次积分及其算法化的工作有文献[11-15].文献[16]中给出了构造一种多项式乘积形式的积分因子算法,此算法主要通过待定参数法寻找不变代数曲线,进而构造首次积分.文献[17]通过寻找不变代数曲线,构造积分因子,得到多项式系统的首次积分.从而得到了一个二维Kolmogorov系统的中心条件.

另一种方法就是利用有理可逆性.利用有理可逆性产生中心就是通过代数映射,使得系统关于某一直线不变且时间反向,从而得到中心.文献[18]考虑了时间可逆与中心问题的关系,指出了系统经线性变换、双线性变换、有理变换等变换下,成为Poincare对称系统的充要条件,得到了系统为中心的充分条件.

本文在Wang[8]利用焦点量法得到中心的4组充分条件的基础上,采用代数对称法得到了不同于文献[8]的3组新的中心的充分条件.

2 三次微分系统中心条件

考虑三次微分系统[8]:

(3)

文献[8]通过焦点量法得到了系统(3)的4组充分条件.

定理2.1[8]三次微分系统(3)满足以下条件之一,则原点必为系统中心：

1)A-B=F=E=D=C=0;

2)D+E=A-B=C+F=a-b=0;

3)D+E=A-B=C+F=a+b=0;

4)E+3C=D+3F=A-B=0.

系统在条件1)或4)下满足首次积分

在条件2)下,系统关于直线x+y=0对称,在条件3)下,系统关于直线x-y=0对称,满足Poincare对称原理.

一个自然的问题,是否存在过原点的直线

sx+ty=0,s2+t2≠0

使得系统(3)关于该直线对称?利用如下的定理2.2给出系统(3)存在中心的新条件.

定理2.2[9]向量场ζ关于过原点直线

sx+ty=0,s2+t2≠0

时间可逆的充要条件是存在非退化线性变换S:R2→R2,使得S(x,y)为(x,y)关于直线

sx+ty=0,s2+t2≠0

的对称点,且满足

S(P(x,y),Q(x,y))=

-(P(S(x,y)),Q(S(x,y))),

(4)

其中

M1=-12As5t+40As3t3-12Ast5+12Bs5t-
40Bs3t3+12Bst5-4Es4t2+4Es2t4-
2Fs6+2Fs4t2-2Fs2t4+2Ft6,

M2=48As3t-48Ast3-48Bs3t+48Bst3+
Ds4+2Ds2t2+Dt4-2Es4+
8Es2t2-2Et4+3Fs4-6Fs2t2+3Ft4,

M3=3as2t-at3-bs3+3bst2,

M4=20As5t-152As3t3+20Ast5-20Bs5t+
152Bs3t3-20Bst5-2Es6+10Es4t2-
10Es2t4+2Et6-12Fs4t2+12Fs2t4,

M5=16As3t-16Ast3-16Bs3t+16Bst3-
Cs4-2Cs2t2-Ct4-Es4+
2Es2t2-Et4-4Fs2t2,

M6=16As3t-16Ast3-16Bs3t+
16Bst3+4Cs2t2+Ds4-2Ds2t2+Dt4+
Fs4+2Fs2t2+Ft4,

M7=20As5t-152As3t3+20Ast5-20Bs5t+
152Bs3t3-20Bst5+12Cs4t2-12Cs2t4+
2Ds6-10Ds4t2+10Ds2t4-2Dt6,

M8=48As3t-48Ast3-48Bs3t+
48Bst3-3Cs4+6Cs2t2-3Ct4+2Ds4-
8Ds2t2+2Dt4-Es4-2Es2t2-Et4,

M9=-12As5t+40As3t3-12Ast5+12Bs5t-
40Bs3t3+12Bst5+2Cs6-2s4t2+
2Cs2t4-2Ct6+4Ds4t2-4Ds2t4.

(5)

利用结式方法[19]对M1、M2、M3、M4、M5、M6、M7、M8、M9关于s消元后,取M1与M2,M1与M5,M2与M4,M4与M5,M6与M7,M7与M8做结式后的非平凡因式分别记为Q1,Q2，…，Q6如下:

Q1=108A2D-216A2E-540FA2-216BDA+
432BEA+1 080FBA+108DB2-216EB2-540B2F-
D3+3D2E+6D2F-6DEF-9DF2-4E3-12E2F-9EF2,

Q2=12A2C+12A2E+32FA2-24ABC-24BEA-
64FBA+12B2C+12EB2+32B2F-C3-2C2E-
5C2F-CE2-6CEF-8CF2-E2F-4EF2-4F3,

Q3=140A2D+392A2E+420FA2-280BDA-
784BEA-840FBA+140DB2+392EB2+420B2F-
D3-D2E-6D2F-6DEF-9DF2-9EF2,

Q4=140A2C-84A2E-280ABC+168BEA+140B2C-
84EB2-9C3-6C2E-9C2F-CE2-6CEF-E2F,

Q5=84A2D-140FA2-168BDA+280FBA+84DB2-
140B2F+CD2+6CDF+9CF2+D2F+6DF2+9F3,

Q6=420A2C+392A2D+140A2E-840ABC-784BDA-
280BEA+420B2C+392DB2+140EB2-9C2D-
9C2E-6CDE-6CE2-DE2-E3.

(6)

再对Q1,Q2,…,Q6关于A两两做结式,取Q3与Q4,Q3与Q5,Q4与Q5,Q4与Q6,Q5与Q6做结式后的结果分别记为:

Q11=784(3C+D+E+3F)2(15C2D+42C2E+
45C2F-5CD2-9CDE-15CDF+14CE2+
15CEF+3D2E+9DEF+14E2F)2,

Q22=784(3F+D)4(14CE+15CF+5CD+
9EF+3ED+15F2+3D2)2,

Q33=784(C+F)2(27C2D-45C2F+5CD2+
18CDE+30CDF-30CEF+45CF2-3D2E+
3DE2-18DEF-5E2F-27EF2)2,

Q44=784(3C+E)4(15C2+15CF+
9CD+3E2+5EF+3ED+14FD)2,

Q55=784(3C+D+E+3F)2(14CD2+9CDE+
15CDF-15CEF+45CF2+14D2F+3DE2-
9DEF+42DF2-5E2F+15EF2)2.

最后,对Q11、Q22、Q33、Q44和Q55的第三个因子两两分别关于C、D、E、F做结式,并取Q22的第三个因子与Q44的第三个因子关于C、D、E、F做结式,其结果如下：

(7)

由(7)式可得:

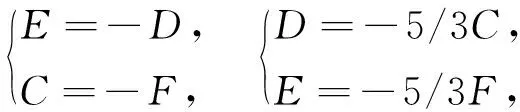
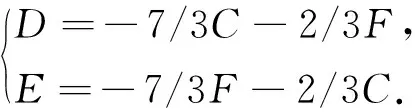
(8)

将(8)式的第一组条件C=-F,E=-D代入M1、M2有:

R1=-12As5t+40As3t3-12Ast5+12Bs5t-
40Bs3t3+12Bst5+4Ds4t2-4Ds2t4-2Fs6+
2Fs4t2-2Fs2t4+2Ft6,

R2=3(s-t)(s+t)(16Ast-16Bst+
Ds2-Dt2+Fs2-Ft2).

特别地,对R1、R2关于s做结式有:

(A-B)4(-5F+3D)2(64A2-

128AB+64B2+D2+2FD+F2)2.

(9)

当A-B=0或-5F+3D=0时,(9)式为0.而A-B=0这一情形在文献[7]中已经讨论.因此,现在只需考虑-5F+3D=0.再由C=-F,E=-D代入(5)式得到:

T1=-2/3(s2-3t2)(3s2-t2)(6Ast-
6Bst+Fs2-Ft2),

T2=8(s-t)(s+t)(6Ast-6Bst+Fs2-Ft2),

T3=3as2t-at3-bs3+3bst2,

T4=2/3(5s4-38s2t2+5t4)(6Ast-6Bst+Fs2-Ft2),

T5=8/3(s-t)(s+t)(6Ast-6Bst+Fs2-Ft2),

T6=8/3(s-t)(s+t)(6Ast-6Bst+Fs2-Ft2),

T7=2/3(5s4-38s2t2+5t4)(6Ast-6Bst+Fs2-Ft2),

T8=8(s-t)(s+t)(6Ast-6Bst+Fs2-Ft2),

T9=-2/3(s2-3t2)(3s2-t2)(6Ast-
6Bst+Fs2-Ft2).

通过上式可以得到,当Ti=0(i≠3)时必有

6(A-B)st+F(s2-t2)=0.

由T3=0得

3as2t-at3-bs3+3bst2=0.

消去s和t可得

54A3ab-162A2Bab+27A2FA2-27A2FB2+
162AB2ab-54ABFA2+54ABFB2-
18AF2ab-54B3ab+27B2FA2-
27B2FB2+18BF2ab-F3A2+F3B2.

(10)

从(8)式第一组解,(9)式第二个因式和(10)式可得到一组解:

C=-3/5D,E=-D,F=3/5D,
a=2,b=11,A=-3+B,D=20.

(11)

将其代入(5)式得

(12)

显然W1,W2,…,W9的公因式为-2t+s.我们能找到这样的直线2x+y=0,使得系统(3)关于该直线对称.

类似地,由(8)、(9)和(10)式还可以得到另外2组参数条件

C=-3/5D,E=-D,F=3/5D,a=18,

b=26,A=-8+B,D=30,

(13)

和

C=-3/5D,E=-D,F=3/5D,a=9,

b=-46,A=-5+B,D=60.

(14)

系统在条件(13)、(14)下,分别关于直线

3x+y=0, 3x+2y=0

对称.

定理2.3三次微分系统(3)满足以下条件之一,则原点必为系统中心:

1)A=-3+B,C=-12,D=20,E=-20,F=12,a=2,b=11;

2)A=-8+B,C=-18,D=30,E=-30,F=18,a=18,b=26;

3)A=-5+B,C=-36,D=60,E=-60,F=36,a=9,b=-46.

由前面的讨论可知,在1)、2)、3)条件下,系统分别关于直线

2x+y=0, 3x+y=0

和3x+2y=0对称.

3 讨论

平面系统的中心焦点判定问题及小扰动极限环的构造是研究热点,其所以受到广泛持久的关注,源于它与Hilbert第十六问题及弱化Hilbert第十六问题之间存在密切的联系.Wang[20]利用焦点量法得到了三次微分系统中心的4组充分条件.徐金亚[20]采用极坐标的形式计算焦点量,得到了形如P(2,2n)Poincare系统原点为中心的条件.本文采用代数对称法得到系统(3)新的三组中心充分条件.一个自然的问题,我们能否通过Darboux积分法得到系统(3)新的中心条件?这个问题可作为进一步研究的课题.