不等距风扇降噪研究

翟术风 上官文斌

（1.广州民航职业技术学院，广东 广州 510403；2.华南理工大学，广东 广州 510640）

【关键字】基频；不等距风扇；降噪

0 前言

据国外相关研究表明,城市噪声主要来源于交通噪声,而交通噪声主要来源于汽车噪声。汽车噪声主要是由发动机、车身与空气的相互作用、轮胎与地面的作用以及传动系统等产生的噪声源组成的，因此汽车是一个包含不同类型汽车噪声的综合噪声源[1]。研究表明，不同性质的汽车噪声的特性以及所占总声能的百分比均是不同的，其中影响最大的就是发动机产生的噪声。发动机产生的噪声源包括进排气噪声、介质燃烧噪声、机体各部件振动辐射噪声、冷却散热风扇的噪声以及其他附件产生的噪声。在过去很长一段时间内，由于自主品牌汽车企业技术起步较晚，造成国内的冷却风扇技术相比于国外具有很大不足，开发模式依然是逆向开发，技术上的严重滞后使得冷却风扇质量上也有一定的缺陷。为了保证发动机的散热效果，延长发动机的使用寿命，各大厂家和工程师们也在不断研究冷却风扇的有效降噪措施以及性能方面的改进。其中，针对风扇结构上的改进是一个重要的研究方向，一直有新观点被提出，自从1967年 Lowson M.V.[2]提出采用风扇叶片周向随机布置的方式降低轴流式压缩机基频噪声的想法后，该想法被各国学者不断地应用并发展出了多种设计方法，进行不等距叶片风扇的研究对于提高发动机冷却风扇的性能和降低冷却风扇的噪声具有一定的工程实用价值和研究意义。

Lowson M.V.[2]最先提出了采用风扇叶片周向随机布置的方式降低轴流式压缩机基频噪声的观点，并推导出了等距叶片转子的声辐射公式。Mellin R.C.等[3]研究了叶片周向不等距分布调制噪声的频谱特性，推导出计算不等节距轴流风扇的离散噪声的公式，给出了4至15叶片数的轴流风扇叶片的最佳周向分布方式。Ewald D.[4]等采用半经验的贝塞尔函数方法将一个叶片数为22的轴流风扇的BPF噪声降低了8dB，并提出了另外两种用于预测不等距风扇的分析方法，分别是脉冲近似和正弦波近似的傅里叶变换分析。

Yong Cho等[5]用非结构化三角网格求解算法对二维不可压缩的Navier-Stokes方程进行精确求解，计算了横流风扇的不稳定粘性流场，通过计算可变节距的横流风扇的性能与气动噪声，表明用A型随机节距叶轮可以使叶片通过频率下的旋转噪声发生调制，相比于等距风扇的BPF噪声降低了5.7dB。Brentner K.S.[6]和Sullivan B.M.[7]等人定量研究了直升机主转子采用不等距叶片的噪声情况，结果表明调制叶片间距能降低主转子的A声级声压但并没有使转子的噪声有主观改善。

国内对于对于轴流风扇的研究不多，对不等距叶片的研究大多针对离心风扇和贯流风扇。在轴流风扇的研究上，孙晓峰[8]从叶轮离散噪声计算出发，探讨了轴流式风扇不等距叶片对基频噪声的影响，根据S.E.Wright[9]的BLH理论导出了不等距风扇的声辐射公式。并指出，不等距与等距的相对变化在较大范围内不会对风扇气动性能产生大的影响。徐嘉甫[10]将叶片的不等距设计应用在电机风扇上，探究了叶片不等间隔大小和排列次序变化对谐波强度的影响，分析了不等距风扇的降噪机理，并设计了使感觉噪声PNL最小的风扇叶片间隔角。

本文的研究对象是发动机轴流不等距叶片风扇，从冷却风扇噪声方面着手，阐述了不等距风扇气动噪声的建模方法与计算方法，建立了与实际情况一致的风扇气动噪声仿真模型，利用Fluent计算了不等距叶片风扇的旋转噪声，并与试验结果做了对比，验证了该计算方法的正确性，最后对不等距风扇的噪声频谱曲线做了详细分析。

1 噪声实验

对不等距风扇进行气动噪声试验，按照标准，在半消声室中进行不等距风扇实物的气动噪声试验，半消声室与气动噪声测试装置如图1所示。半消声室及实验设备由宁波雪龙集团有限公司提供，长度为4m，宽度为3.8m，高度为3.4m，实验室后侧装有电机，通过驱动轴与不等距风扇轮毂相连，带动风扇转动。

2 噪声仿真模型

本文计算不等距风扇的气动噪声采用CFD仿真的方法，其中气动噪声计算采用大涡模拟(LES)算法。首先忽略风扇支架、驱动轴和护风圈等部分，坐标原点设在风扇的质心，Z轴与风扇中心轴线重合，气流下游方向为正向，建立半消声室流场模型如图2所示。

首先在hypermesh里对建立的不等距风扇几何模型进行面网格的划分，划分结果与风扇面网格尺寸为2mm-6mm。其次风扇旋转区划分体网格，受风扇面网格尺寸大小的限制，风扇旋转区的体网格也比较小，最大尺寸为6mm。再对半消声室流场模型划分体网格，由于进出口区的气流比较稳定且要控制网格总数，所以进口区和出口区的体网格尺寸较大，而为了使其与旋转区体网格之间在尺寸上逐渐过渡，分别在进口区与风扇旋转区之间，以及出口区与风扇旋转区之间增加过渡区R2和过渡区R3。

由于风扇面网格为三角形，风扇旋转区最适用的体网格类型为四面体网格，通过在外圆柱面上划分三角形面网格，再与风扇面网格一起闭合生成旋转区的四面体网格。由于同样的原因，进口过渡区的体网格也采用四面体网格。逐渐过渡，出口过渡区的体网格采用五面体网格，而在进口区和出口区，为了减少体网格数量，采用的体网格类型为六面体网格。最终得到的划分结果为旋转流体区体网格总数为1.28×106，两个过渡区体网格总数为5.72×105，进口区和出口气体网格总数为2.34×105，半消声室仿真模型体网格总数为 2.08×106。

将上步在Hypermsh软件中划分好网格的模型导入到前处理软件Gambit中设立边界条件。确定边界条件时，将模型的进口平面设为压力进口边界，进口压力为0；模型的出口平面设为压力出口边界，出口压力为0；风扇的表面设为旋转壁面边界；其余的表面被缺省设置为静止壁面边界。将过渡区与进出口区域接触的面设为非一致网格边界，使得六面体网格与四面体网格结合起来，满足软件计算要求。

首先进行稳态流场计算，求解器选择Steady，湍流模型选择RNG k-ε，求解器选择基于压力的分离式求解(Pressure-Based)，在分离求解器中，定常状态计算选择压力速度耦合方程组的SIMPLE算法。对于离散方法的使用，梯度选项设为格林-高斯基于节点，压力设为标准格式，动量设为一阶迎风格式，湍流动能与湍流耗散率设为二阶迎风格式。进出口边界湍流强度与湍流直径分别设为5%和10m。使用多重参考模型（MRF模型）对旋转区进行处理，其他区域使用绝对静止坐标系，在交界面处则利用相对速度方程进行转化。当监测的各项残差小于 1×10-4时，认为稳态计算收敛。

稳态计算收敛后，将稳态计算得到的流场各数值结果作为初场进行瞬态计算，将湍流模型改为LES大涡模型，使用动网格系（DM模型）对旋转区进行处理，在分离求解器中，非定常状态计算选择压力速度耦合方程组的PISO算法，湍流动能设为PRESTO格式。检测面处的迭代模式设为Time Step，最后引入FW-H噪声求解模型计算，设定好噪声接收点与噪声源，经过FFT变换后可得各监测点的频谱曲线，研究风扇气动噪声的特性。风扇气动噪声的计算流程如图3所示。

3 结果与分析

选取风扇工作区间内的六组转速(1800rpm、2100rpm、2400rpm、2700rpm、3000rpm 和 3300rpm)进行计算，图4为不等距风扇气动噪声的试验值与计算值对比图。

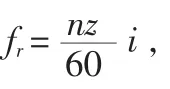
不等距风扇的仿真值与试验值并不是完全相同，仍然有一定的误差，可能是因为：忽略了地面对声波的反射以及散射等作用；简化了不等距风扇的模型和一些配件；建立的有限元仿真模型与实际试验的模型仍然有差距。

FW-H方程[11]：

式（1）右边的三项分别代表单极子源、偶极子源和四极子源，G为基于自由空间的格林函数。

利用FW-H噪声求解模型将所有监测点处压力参数进行快速傅里叶变换（FFT），便可得到各监测点声压级(SPL)的频谱曲线，如图 5所示。

由图5不等距风扇的声压级频谱曲线可以看出，风扇气动噪声随着频率的增大逐渐降低，在低频处声能高，而高频处声能低，最后趋于平缓。旋转噪声和涡流噪声的声压级-频率特性完全不同，旋转噪声是以离散的峰值形式表现在基频及倍频处，而在其他频率处则是连续宽频的涡流噪声。特别是当风扇高速旋转时，冷却风扇内部产生的空气流场较复杂，风压速度等数据不会一成不变，而是瞬时的不断产生变化，复杂的流场导致了涡流噪声在高频范围内很容易产生，因此旋转噪声在低频处特别是前几阶谐波处峰值明显，而在高频范围内对应的各阶次谐波则表现相反，影响较小。

4 总结

阐述了发动机冷却风扇的噪声产生机理及噪声的分类特征，并详细介绍了测试气动噪声的半消声室与噪声采集设备及其测试与计算的原理。接着对不等距风扇进行了数值计算，建立了不等距风扇的半消声室仿真模型，对模型进行网格划分，在对模型进行设置后便开始进行仿真计算，并将仿真计算结果与试验结果进行对比验证。

气动噪声计算值与试验值的数据对比表明，发现CFD仿真方法的精度非常高，其相对于试验的误差不超过4%，验证了使用CFD方法预测风扇气动噪声的可行性。并得到了该不等距风扇的噪声类型、各主要阶次噪声的声能占比等数据。对风扇气动噪声的有限元模型与仿真方法对于风扇气动噪声的预测与研究提供了铺垫。