假设检验中关于检验问题探讨
2018-10-08王丽丽
王丽丽
(合肥学院数学与物理系,安徽 合肥 230601)
假设检验是推断统计的重要组成部分。推断统计是一种根据样本数据来推断总体特征的方法,它是在对样本数据描述的基础上,以概率的形式对总体的未知特征(如均值、方差、分布等)进行表述。利用样本数据对总体特征的推断通常分为两种情况:参数假设检验与非参数假设检验检验。假设检验所依据的原理是小概率原理。其基本思路是首先对总体参数或分布形式作出某种假设,然后利用样本信息以一定的概率来判断原假设是否成立。根据假设检验的基本思想,假设检验可归纳为四个基本步骤:
(1)根据具体的问题,建立原假设和备择假设。 原假设一般是研究者想收集证据予以反对的假设;备择假设一般是研究者想收集证据予以支持的假设。由于假设检验中只有在小概率事件发生的情况下才拒绝原假设,因此在假设检验过程中原假设是受到保护的。它们有三种形式:双侧检验、左侧检验、右侧检验。采用哪种形式要根据实际问题。
(2)构造一个合适的统计量,计算其抽样分布。
(3)给定显著性水平α,确定临界值,拒绝域和接受域。
(4)根据样本的值计算统计量的数值并作出决策。从概率的角度来讲,如果统计量取值的概率小于或等于显著性水平,表明小概率事件发生了,因此拒绝原假设,反之,不能拒绝原假设。(P值)如果统计量的值正好落在拒绝域内,那么拒绝原假设,如果落在接收域内,则不能拒绝原假设,如果正好等于临界值,也要拒绝原假设。
我们这里重点讨论参数假设检验中的T检验。T检验作为参数假设检验的重要方法,在生产与实践中有着广泛的应用。T检验也需要经过上述四个基本步骤,我们应重点研究不同T检验的目的、前提条件和相应的统计量。
1 单样本T检验
单样本T检验的目的是根据总体的样本数据,推断总体的均值与待检验值之间是否有显著差异。它是对单个总体均值的假设检验。
单样本T检验指的是研究问题中仅有一个总体,其前提是样本数据来自服从正态分布或近似正态分布的总体,且总体方差未知。
1.1 单样本T检验的统计量
假设总体分布为正态分布 N(μ,σ2),T检验统计量的数学定义为:
式中,S为样本均方差,T统计量服从自由度为n-1的T分布。
SPSS 软件自动将样本均值、μ0、样本方差、样本量代入式(1),计算出T统计量的观测值和对应的概率P值。
1.2 单样本T检验的应用举例
例1:成虾的平均体重一般为21g。在配合饲料中添加0.5%的酵母培养物饲养成虾时,随机抽取16只对虾,体重为(单位:克)
试检验添加0.5%的酵母培养物饲养成虾时是否提高了成虾体重?
解:SPSS输出结果如下:
p=0.041<0.05,所以拒绝原假设 Test Value=21,又因为样本均值21.519>21,认为在饲料中添加酵母培养物显著提高了成虾体重。
2 两独立样本T检验
两独立样本T检验的目的是根据两个总体的独立样本,推断两个总体的均值是否有显著差异。
该检验的前提条件是:两个总体服从正态分布或近似正态分布;且两样本相互独立,即来自一个总体的样本与来自另一总体的样本互相不影响,两组样本的样本量相等也可以不相等。
2.1 两独立样本T检验的统计量
于是,两个总体均值差检验的检验统计量为T统计量,表达式为:
式中,由 于 μ1-μ2=0(原 假 设 ),故 略 去 。 在第一种情况下,式(5)服从自由度为 n1+n2-2的T分布;在第二种情况下,服从修正自由度的T分布,修正自由度为:
所以两总体方差相等与否是计算抽样分布方差的关键。因此,有必要对两总体方差是否相等进行统计检验。该原假设是:两个总体方差无显著差异,表述为:
SPSS中通过Levene F方法进行检验。Levene F方法是通过判断两样本的方差是否相等来间接推断两个总体的方差是否存在差异的。SPSS软件将自动计算F统计量和概率P值,并将两样本的均值、样本量、抽样分布方差等代入式(5),计算T 统计量的观测值和相应的概率P值。
2.2 两独立样本T检验的应用举例
例2:为了估计两种方法组装产品所需要时间的是否存在显著差异,分别对两种不同的组装方法随机安排12个工人,每个工人组装一件产品所需的时间(分钟)。

表2 两种方法组装产品所需的时间
试以5%的显著性水平判断两种方法组装产品所需的时间是否存在显著差异。
解:SPSS输出结果如下:
在 Levene’s Test for Equality of Variances (方 差齐性检验)中,F=.011,p=0.917>0.05,接受原假设,即认为方差是齐的。从而,看方差齐那一行的计算结果。此时t-test for Equality of Means(两均值比较的t检验)中,p=0.042<0.05,所以拒绝原假设,认为两种方法下的平均时间存在显著差异。
3 两配对样本T检验
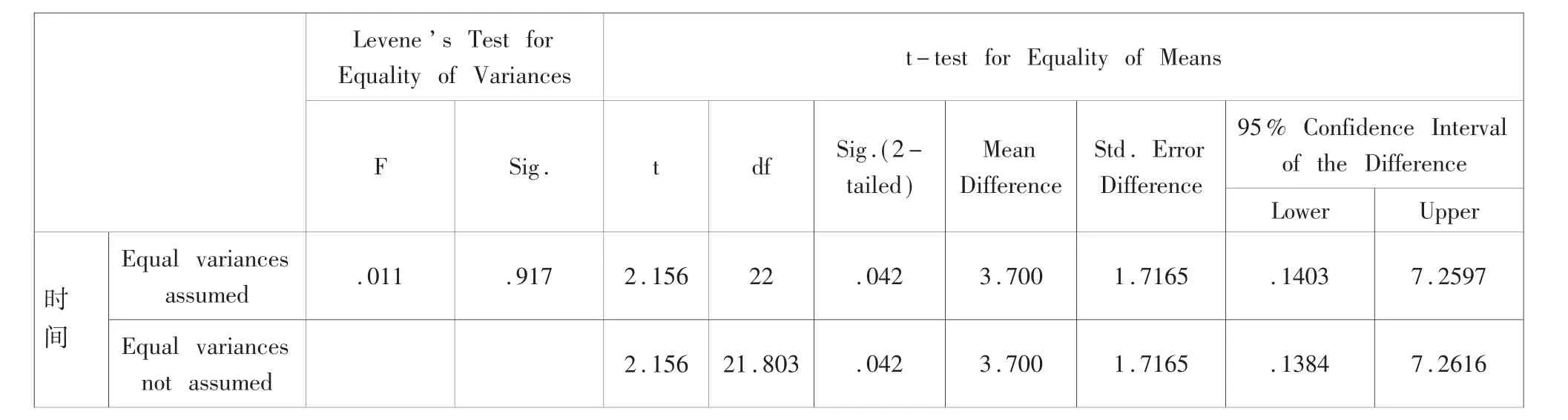
表3 Independent Samples Test
两配对样本T检验的目的是根据两个总体的配对样本,推断两个总体的均值是否存在显著差异。
两配对样本T检验与两独立样本T检验的显著差别是要求两组样本是配对的。配对样本是对某事物两个侧面的描述,也可是在“前”、“后”两种状态下某种属性的两种不同的特征。其中的差别在于抽样是相互关联的,而不是相互独立。
配对样本一般有两个特征:第一,两组样本的样本量相同;第二,两组样本观测值的先后顺序是一一对应的,不能随意更改。
3.1 两配对样本T检验的统计量

表4 10名学生两套试卷的得分
两配对样本T检验是通过转化为单样本T检验来实现的,即转化成推断差值序列总体的均值是否与0存在显著差异,其检验统计量与单样本T检验类似。所以,它要求样本配对,观测值数量相同且顺序不能随意更改。SPSS软件将计算两组样本的差值,并将数据代入式(1),计算出T统计量的观测值和对应的概率P值。

表5 Paired Samples Test
3.2 两配对样本T检验的应用举例
例3:由10名学生组成一个随机样本,让他们分别采用A和B两套试卷进行测试。
试以5%的显著性水平确定两套试卷的平均分有无显著差异。
解:SPSS输出结果如下:
p=0.001<0.05,所以拒绝原假设,认为两份试卷的平均成绩有显著差异。
通过上面的讨论,可以发现三种T检验的分析方法有一些共同之处,即在构造T统计量时,它们的分母都是抽样分布的标准差,分子都是均值之差。但是两独立样本T检验与两配对样本T检验的抽样分布的标准差不同。两配对样本T检验比两独立样本T检验更进了一步,因为它能对观测值自身的其他影响因素加以控制。
