桥梁断面气动导纳风场依赖特性的数值研究
2018-10-08张伟峰张志田张显雄
张伟峰, 张志田, 张显雄
(湖南大学土木工程学院 风工程与桥梁工程湖南省重点实验室, 湖南 长沙 410082)
0 引 言
处于大气边界层中的大跨度桥梁,通常会受到静风力、周期性的涡激力和随机气动力的作用。其中抖振力是由空气中的湍流引起,因此对于实际桥梁是不可避免的。基于条带假定的大跨度桥梁随机抖振理论把来流湍流产生的气动力效应按单位长度的断面气动力和沿跨度方向的空间相关性来处理[1]。通常,沿桥梁跨度方向的相关效应用联合接收函数来表示,而不同波长的湍流对断面的非定常效应则用气动导纳函数来考虑。
气动导纳作为联系随机抖振力和脉动风的传递函数,在桥梁随机抖振分析中起着重要的作用。因此,准确地识别桥梁断面的气动导纳函数,是进行桥梁抖振分析的关键。Sears[2]在势流理论的基础上通过计算竖向简谐脉动风作用下二维薄机翼断面受到的气动力,得到了气动导纳函数。Davenport[1]针对桁架梁桥,提出了顺风向脉动作用下桁架梁桥的阻力气动导纳计算公式。目前,对于钝体的桥梁断面,气动导纳的识别主要以风洞试验为主。按照在风洞中来流湍流的生成方式不同,气动导纳的识别可以分为被动格栅识别方法和主动控制格栅识别方法两种。由于被动格栅的简易性,大量研究者对此进行了详细的研究,如:Sarkar[3]、Larose和Tanaka[4]、Sankaran和Jancauskas[5]、Gu和Qin[6]等。相比于被动格栅,主动格栅需要特殊的装置,因此目前对于主动格栅识别气动导纳的研究还较少[7-9]。与被动格栅相比,主动格栅利用运动机构生成指定的湍流度、湍流积分尺度和功率谱密度的风场,有助于对气动导纳进行更加深入的研究。
除了传统的风洞试验,近年来CFD数值模拟也被用来进行气动导纳的研究。Bruno等[10]通过阶跃函数,识别了一箱梁断面在两种湍流度下的气动导纳函数;Hejlesen等[11]利用二维的离散涡方法,计算了四种桥梁断面的气动导纳函数;唐煜等[12]借助于商用计算流体软件Fluent,计算了平板和箱梁断面在简谐来流下的气动导纳。相比于主动格栅,CFD数值模拟不需要专门的试验设备、易于控制来流的风场特性、可重复性好等优点。在气动导纳的识别上,CFD数值模拟具有巨大的潜力。目前CFD数值模拟虽然已经广泛用于桥梁断面的静气动力[13],涡激力[14],气动自激力[15]等计算,但是利用CFD识别气动导纳的研究尚处于起步阶段。
本文基于二维不可压URANS方法,分别计算了平板、箱梁、双边肋断面在简谐脉动来流和宽频湍流中的非定常气动力,并识别出各自的气动导纳函数。在此基础上,通过考察断面在三种脉动幅值来流下的气动导纳,研究了不同来流特性对各类断面气动导纳的影响。
1 气动导纳识别方法
基于准定常假定的抖振力理论把桥梁断面上的随机气动力看作是静气动力、湍流脉动分量的函数,它忽略了不同频率脉动风对气动力的影响。这在湍流积分尺度远远大于桥梁断面的特征长度时是成立的。当来流的湍流积分尺度与桥梁断面的特征长度处于同一量级时,必须引入气动导纳函数来考虑气动力的非定常效应。在仅有竖向简谐脉动来流作用下桥梁断面的抖振力可以表示为[16]:
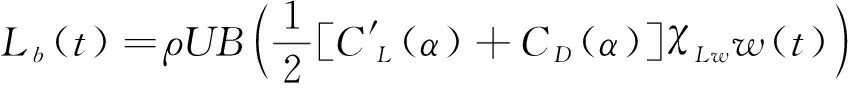
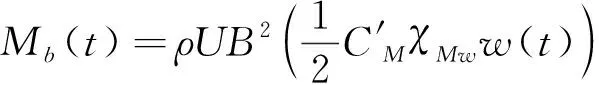
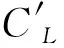
由式(1)和式(2)可以得到升力和扭矩的功率谱密度:
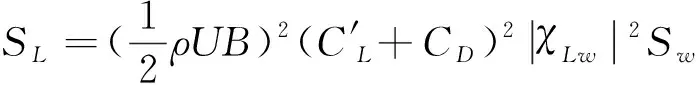
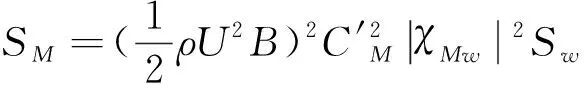
其中,SL和SM分别为升力和扭矩的功率谱密度;Sw为竖向脉动风的功率谱密度;χLw2和χMw2为升力和扭矩关于竖向脉动风的气动导纳。
据式(3)和式(4)可以得到χLw2和χMw2的表达式:
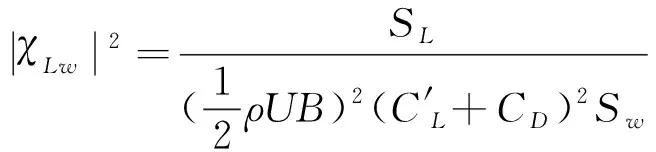
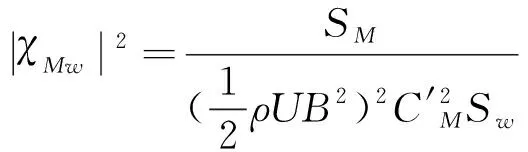
这里也给出Liepmann简化的Sears函数以供参考,如下式所示:

其中k=fB/U,为无量纲频率。
2 CFD数值模型
2.1 数值计算方法
本文数值计算采用三种不同流线程度的断面,分别为:宽高比B/D=103∶1的平板断面,流线型的箱梁断面和钝体的双边肋断面。具体的断面形式如图1所示。

(a) 平板断面

(b) 箱梁断面
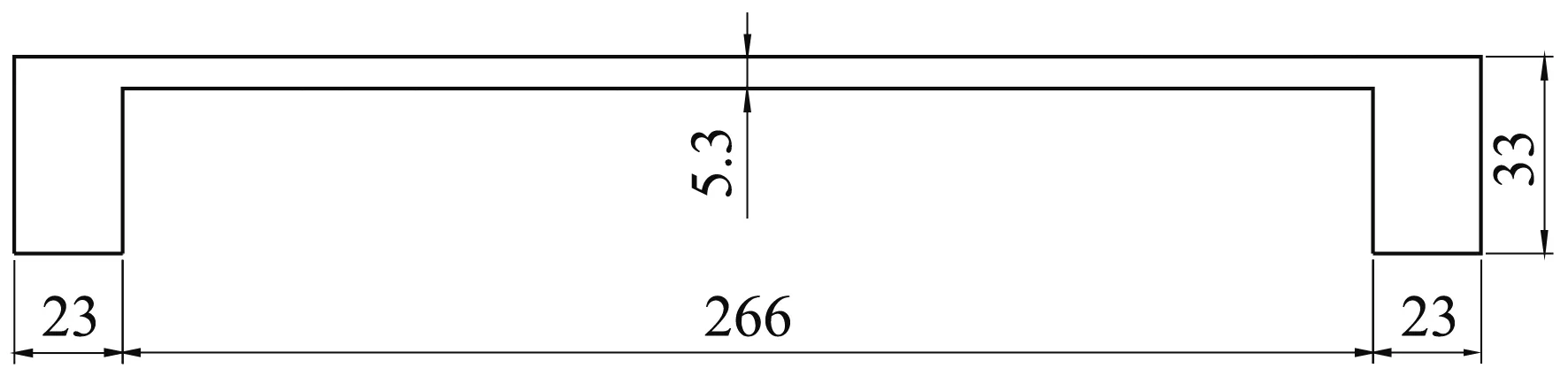
(c) 双边肋断面
绕断面的不可压流动由Navier-Stokes方程控制,通过商用的流体计算软件ANSYS Fluent求解。其中,压强速度的耦合采用PISO方法,时间项的推进采用二阶的隐式格式,对流项的离散采用三阶的MUSCL格式。湍流的模拟采用SSTk-ω湍流模型。在基于RANS方法的湍流模型中,SSTk-ω湍流模型由于对来流特性的不敏感性、对边界层分离和再附的准确预测已经被广泛应用于工程实践中[17-18]。需要注意的是,相比于直接数值模拟(DNS)和大涡模拟(LES),两方程的RANS湍流模型不能捕捉到高频范围的脉动,因此也不能模拟出高频范围内的气动力效应。但是,现代大跨度桥梁关心的折算频率一般位于0~1之间,在本文对应于f=0~25.8 Hz,而RANS湍流模型能够分辨的频率范围要远大于这个范围,如图6所示。
模型的计算域如图2所示。对于简谐脉动来流,计算域的左侧采用速度入口边界条件,水平向速度分量u不随时间变化,竖向速度分量w为正弦脉动;计算域的上下边界也采用速度入口,竖向速度除了随时间变化以外也是空间的函数,以保持与左侧的速度进口相协调。对于宽频湍流来流,计算域左侧的速度入口,水平速度与竖向速度都采用宽频的人工合成湍流;计算域的上下边界采用对称边界条件。右侧的出口都采用压强出口条件。
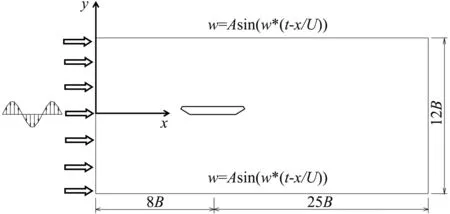
图2 计算域及边界条件Fig.2 Computational domain and boundary conditions
此外,为了保证上下侧边界不对内部的绕流场产生影响,上下侧边界之间的距离应该取得充分大。通过对8B、12B、16B、20B四种工况的计算,结果表明12B的距离可以满足本文的计算需求。
计算域的网格采用混合网格的形式。在靠近模型的范围内采用结构化的四边形网格,近壁面的第一层网格高度yw=1.0×10-4B,可以保证壁面处的y+小于1。在结构化网格之外是三角形的非结构化过渡网格,网格的最大值为2.0×10-3B。此外,对尾流区内的网格进行加密。三角形网格的外面区域采用结构化网格进行填充。如图3为箱梁断面壁面附近的网格。

图3 箱梁断面附近的网格Fig.3 Computational mesh around the box section
2.2 正弦脉动流的数值计算
在无障碍物的流场中,保证来流的主要特征(如:湍流度、积分尺度、功率谱密度等)可以维持到计算域的出口不变,即来流的自保持特性,是CFD计算准确性的基本要求。在基于有限体积法的CFD数值求解器中,误差主要来源于微分方程的离散过程。一般认为,计算域网格的分辨率和时间步长是来流自保持特性的关键影响因素。
对于竖向简谐脉动来流,附加在主流上的竖向脉动速度对应的波长为:
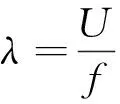
其中f为竖向脉动风的频率。
为了使简谐脉动波在计算域内有效的传播,应保证在一个波长内有足够多数量的网格,即:
λ=NΔx(9)
其中,Δx为网格的尺寸,N为一个波长内的网格数量。
由折算频率k的表达式及式(8)、式(9),可得到用k表达的网格尺寸Δx的表达式:
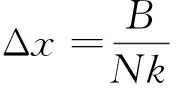
根据唐煜等[12]的研究,当N≥80时可以满足流场中相邻两波峰间幅值的对数衰减率δ=In(Ai+1/Ai)≤ 0.003。其中Ai+1、Ai分别为相邻两波峰间的幅值。
另外,关于时间步长的取值,本文选择在一个简谐脉动周期内保证至少有200个时间步,这比唐煜等[12]建议的无量纲时间步长Δt=dtU/Δx≤1.2要小。
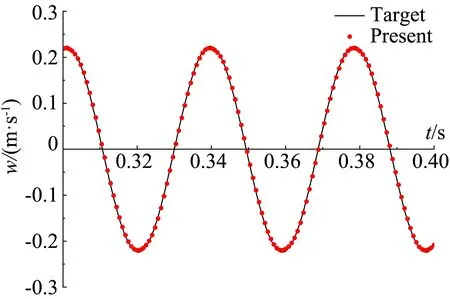
图4所示为k=0.03和k=1时,无障碍流场中坐标(x,y)=(8B,0)处,简谐脉动速度时程与目标值的比较。从图中可以看到,在低折算频率与高折算频率下模拟值与目标值吻合良好,说明采用以上的数值设定可保证来流的自保持特性。
2.3 宽频湍流的数值计算
入口边界处的宽频湍流,采用Davidson[19]等提出的人工谱合成方法。利用该方法可以生成指定湍流度、积分尺度和功率谱密度函数的随机脉动风速时程。本文以Karman谱作为目标风谱,湍流度与简谐脉动来流的湍流度相接近。
为了降低湍流度、湍流积分尺度等湍流特性沿计算域的衰减,模型断面到入口处的网格要足够密。通常我们关心的折算频率k≈0~1之间,参照正弦脉动来流的网格大小,并考虑计算效率的因素,模型断面到入口处的网格取Δx=B/(50×1)。数值离散格式和时间步的取值同样参照正弦简谐脉动来流的设置,即,对流项的离散采用三阶的MUSCL格式,无量纲时间步Δt取1。
图5所示为湍流度和湍流积分尺度沿计算域中心线y=0的变化。从图中可以看出,湍流度和湍流积分尺度从入口进入计算域后都呈现出一定程度的衰减,但是随着入口距离的增大,湍流的演化逐渐平稳,在距离入口1.5 m后湍流度和湍流积分尺度都趋于稳定。

(a) k=0.03
(b) k=1
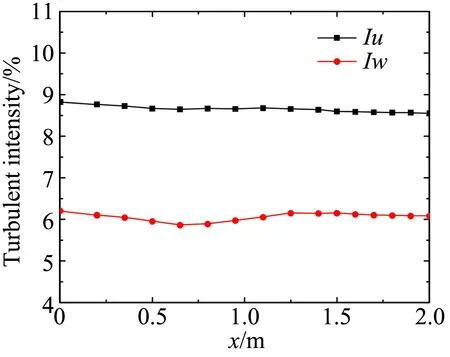
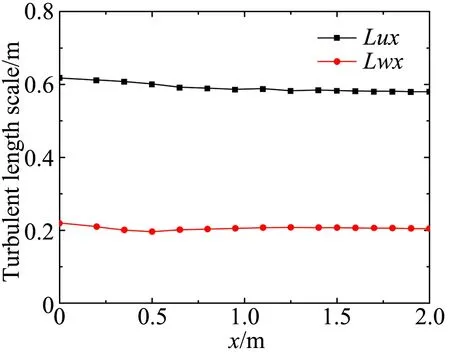
图5 湍流度和积分尺度沿x轴的变化 (y=0)Fig.5 Turbulent intensity and turbulent length scale along the x-axis (y=0)
图6所示为无障碍流场中坐标(x,y)=(8B,0)处竖向脉动风速的功率谱密度与目标值的比较。由图6可见,在我们关心的频率范围内(f<30 Hz),模拟的随机竖向脉动风速功率谱密度与目标值吻合良好。
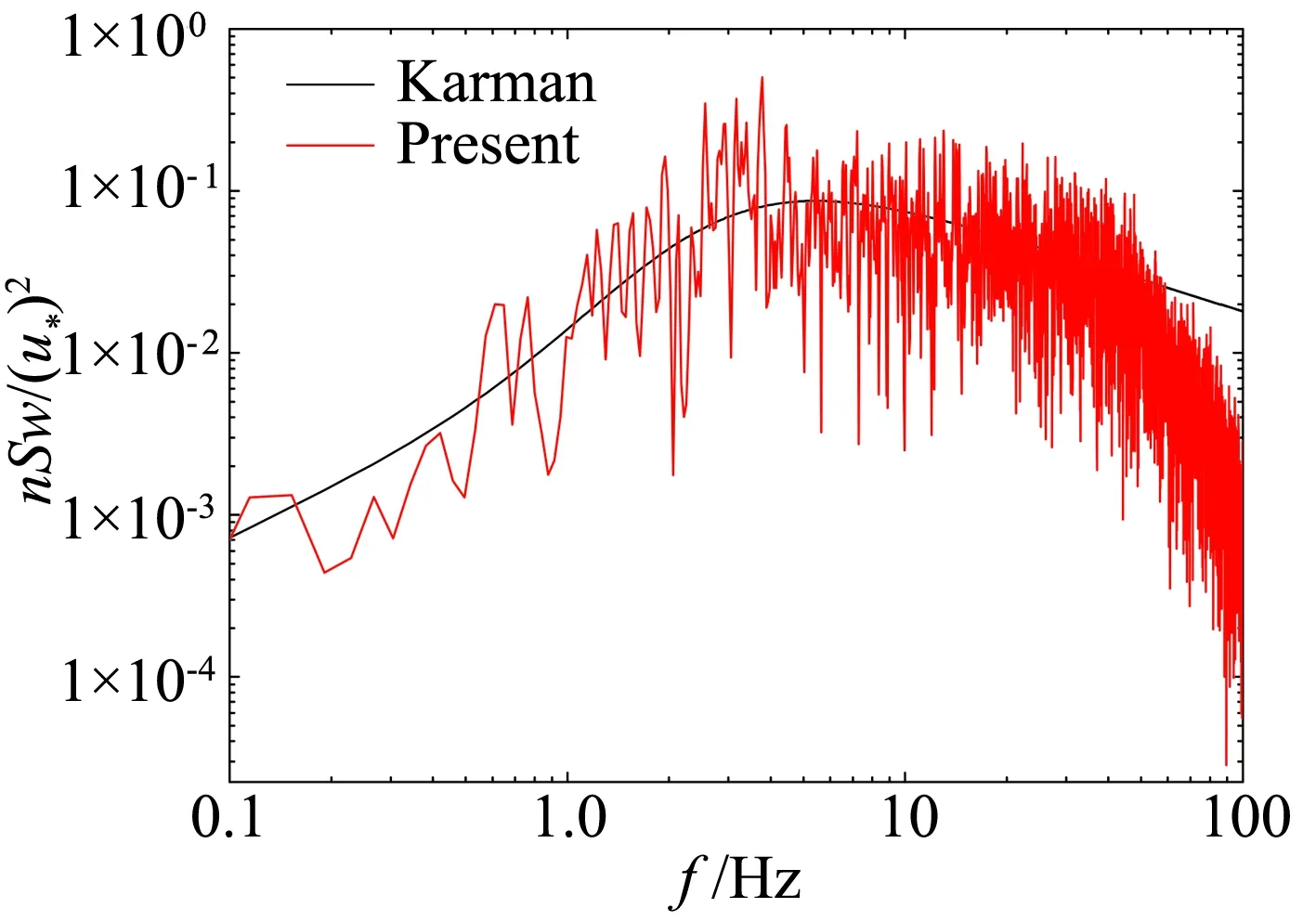
图6 坐标(x,y)=(8B,0)处竖向脉动速度功率谱密度Fig.6 Power spectrum of the vertical gust at (x,y)=(8B,0)
3 数值计算结果
3.1 单频与宽频脉动风下的气动导纳
首先考虑两种来流条件,即单频简谐脉动风与宽频湍流脉动风。两种情况的平均风速均设为8 m/s。对于单频简谐脉动来流,其竖向简谐速度的幅值为0.226,对应的湍流度为2%,而顺风向的湍流度很小可忽略不计;对于宽频湍流来流,竖向脉动速度的湍流度为2%,其顺风向的湍流度与竖向的湍流度基本一致。
在气动导纳识别前,首先在均匀来流的情况下计算出三种断面的静力三分力系数及其对迎角的导数,然后在无障碍物的流场中计算得到桥梁断面中心点处的脉动风速时程。最后在得到桥梁断面受到的三分力时程后,根据本文第一节所述方法可以识别出气动导纳函数。
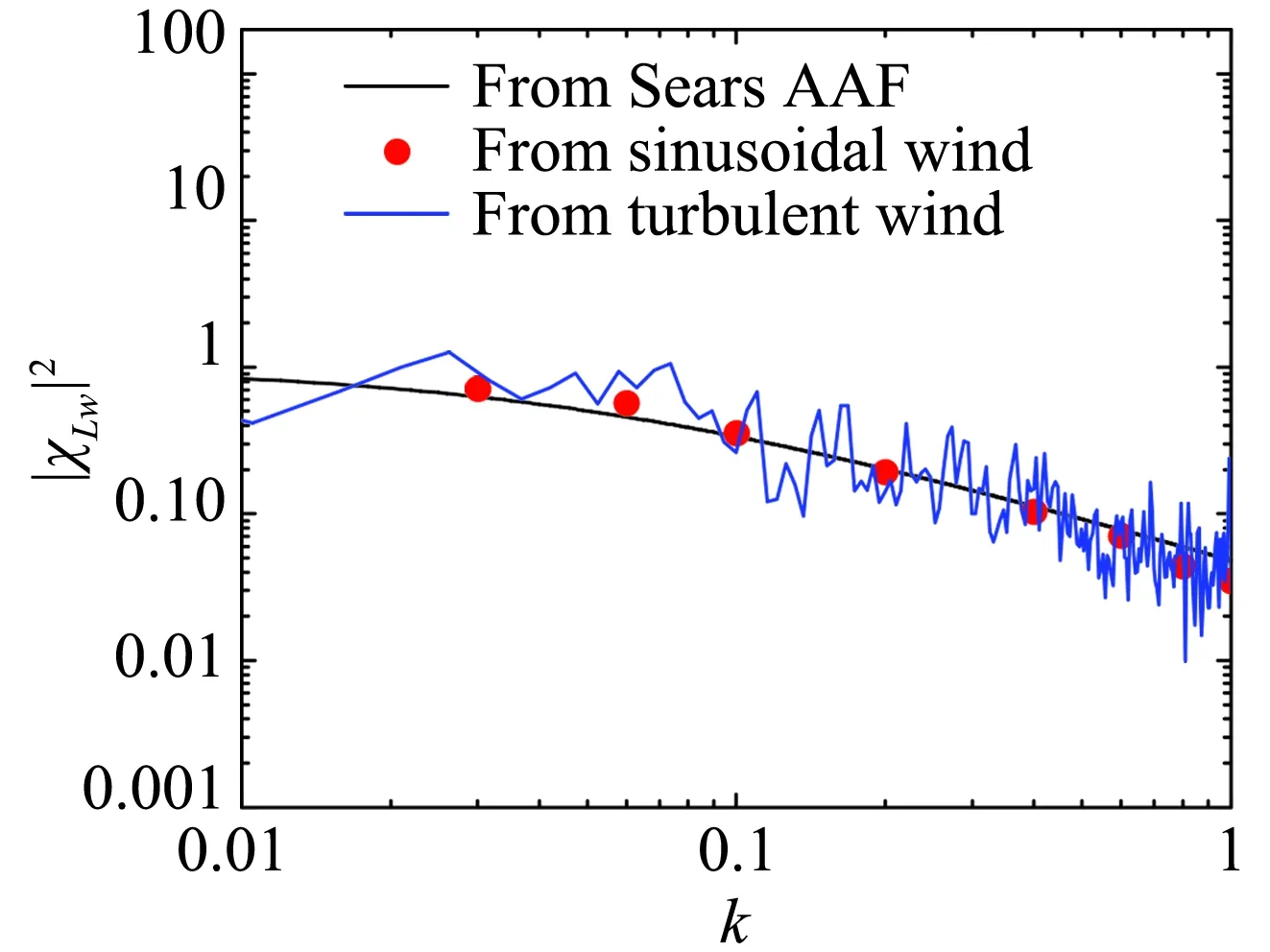
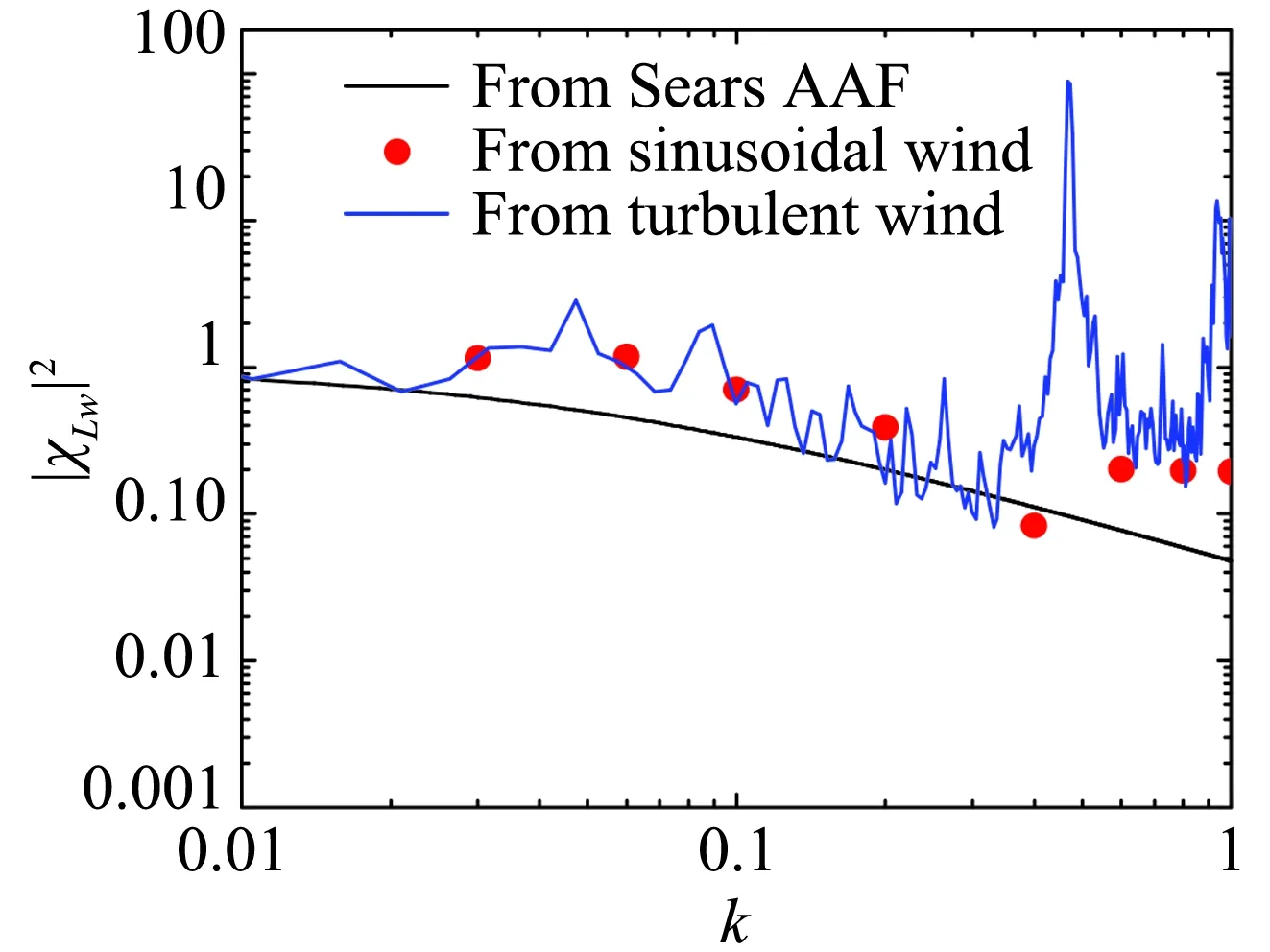
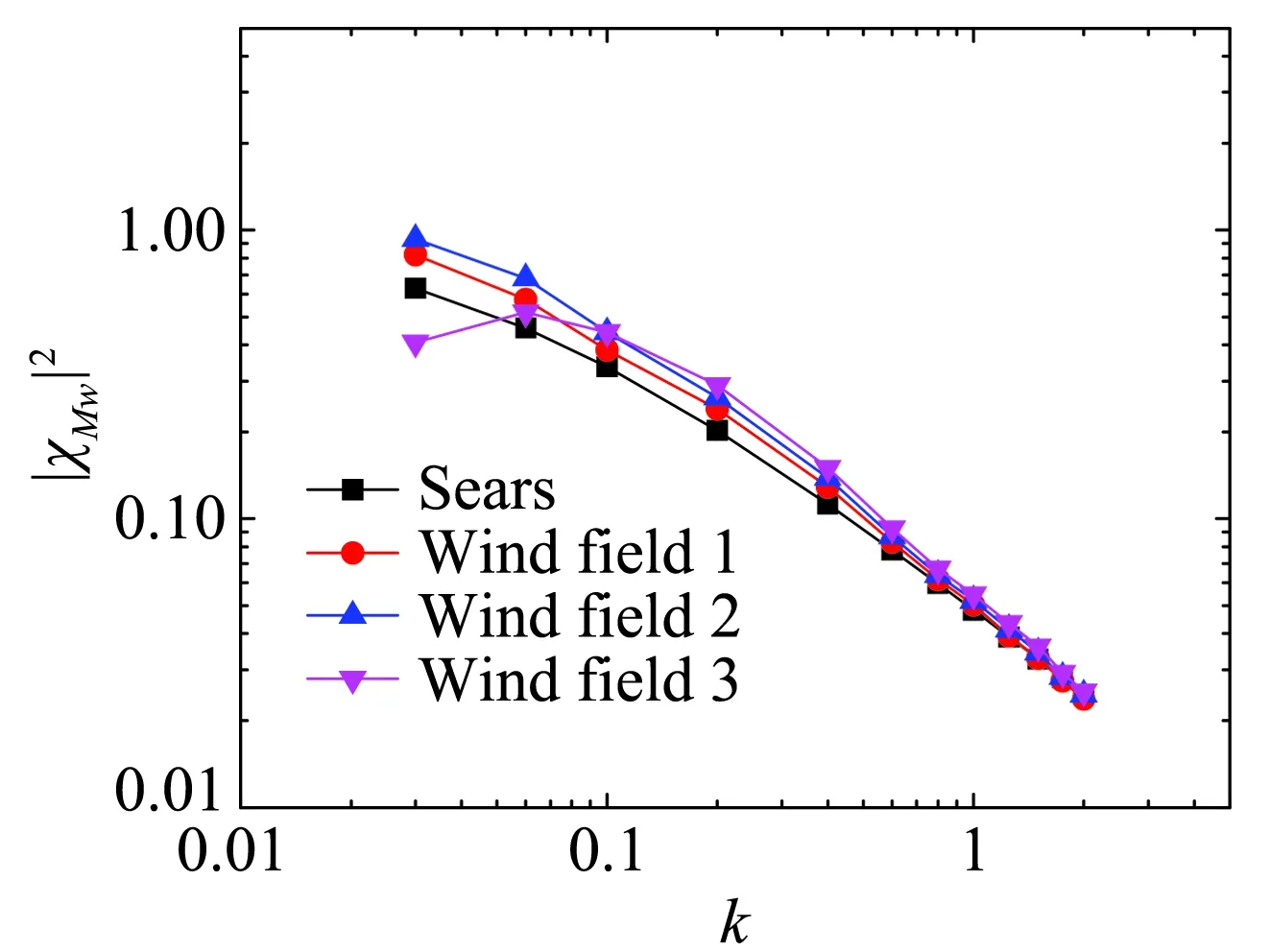
图7分别为平板、流线型的箱梁和钝体双边肋断面在两种不同来流下的气动导纳函数。
理想平板断面的气动导纳,存在理论解,即Sears函数。所以,平板断面可以用来验证本文数值方法的准确性。由图7可知,在竖向简谐脉动来流下,平板断面的气动导纳函数与Sears函数吻合良好,证明了本文数值识别气动导纳的可行性。相比之下,湍流场下的气动导纳函数与Sears函数具有相同的趋势,但却表现出很强的随机跳跃性,与Sears函数之间有实质性的差异。
对于流线型的箱梁断面,数值识别结果与Sears函数相比,在低折算频率范围内与Sears函数相近,而在高折算频率范围内比Sears函数低。双边肋断面的气动导纳函数与Sears函数之间差别明显,这是符合钝体断面特征的合理现象。
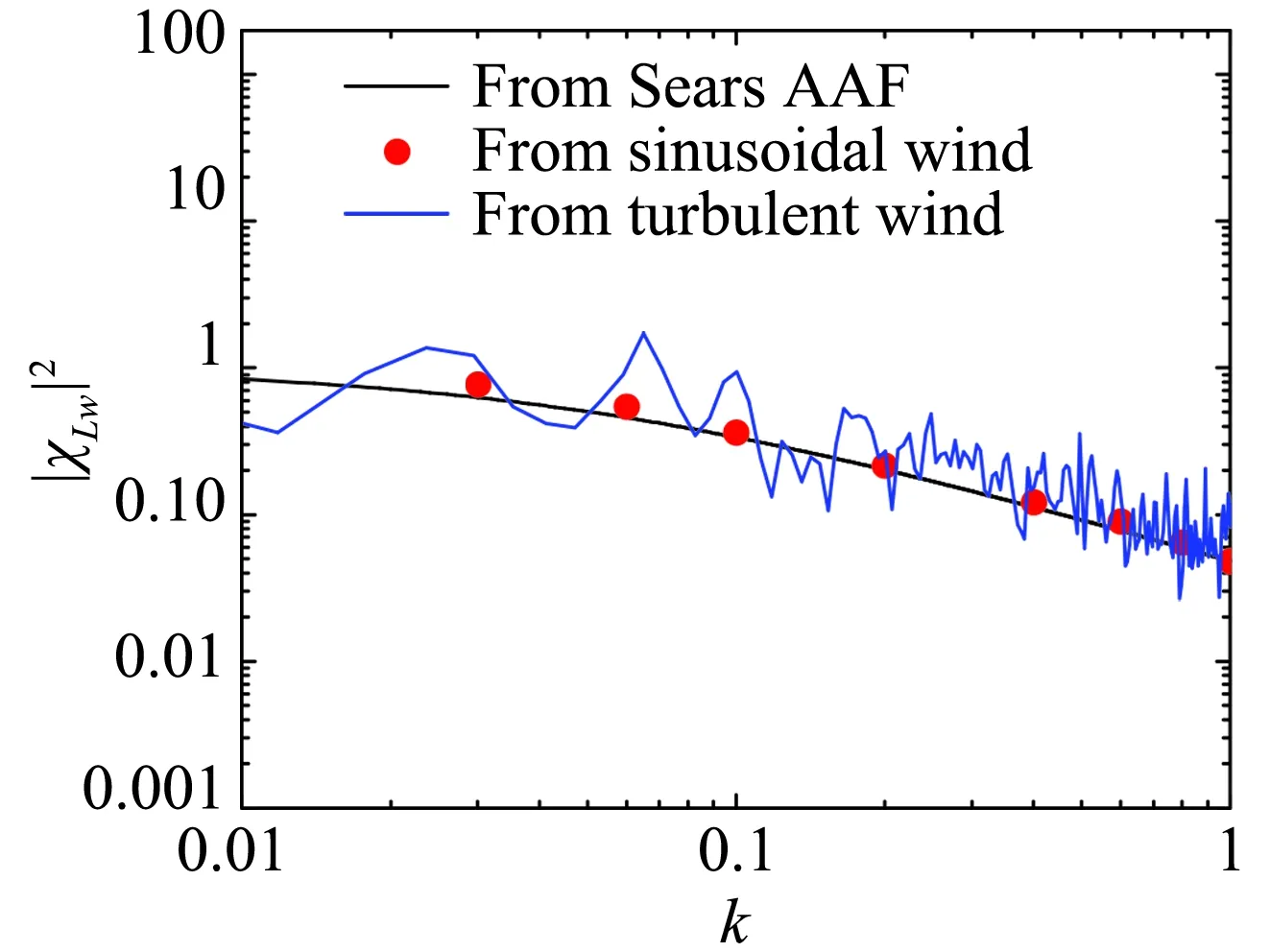
(a) 平板断面
(b) 箱梁断面
(c) 双边肋断面
3.2 单频脉动风幅值对气动导纳的影响
由于桥梁断面的钝体性质,气动导纳一般不存在与理想平板断面类似的理论解。在现代桥梁抖振分析中,某次试验识别的气动导纳经常被应用于任意风场环境下的全桥抖振响应分析。这种做法暗含了气动导纳不随风场特性改变,仅是无量纲折算频率的单值函数。然而,对于钝体断面,一些研究者的试验表明,气动导纳函数除了与断面的形式有关外,还与来流的湍流度、积分尺度等有关[7, 20]。
ANSYS Fluent,通过用户自定义函数(UDF),可以轻易地改变计算域入口边界的来流特性。通过改变简谐脉动来流的幅值,下面讨论简谐脉动风幅值对不同流线型程度桥梁断面气动导纳的影响。
三种简谐脉动来流的特性如表1所示,来流的平均速度都为8 m/s。

表1 CFD计算用简谐来流特性Table 1 Wind properties used in simulations
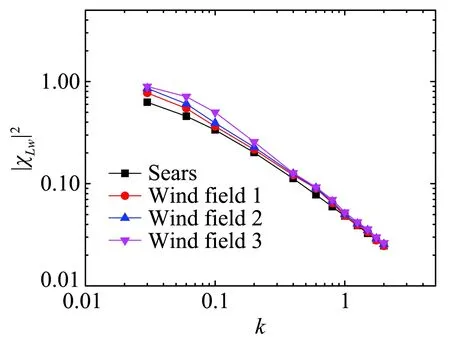
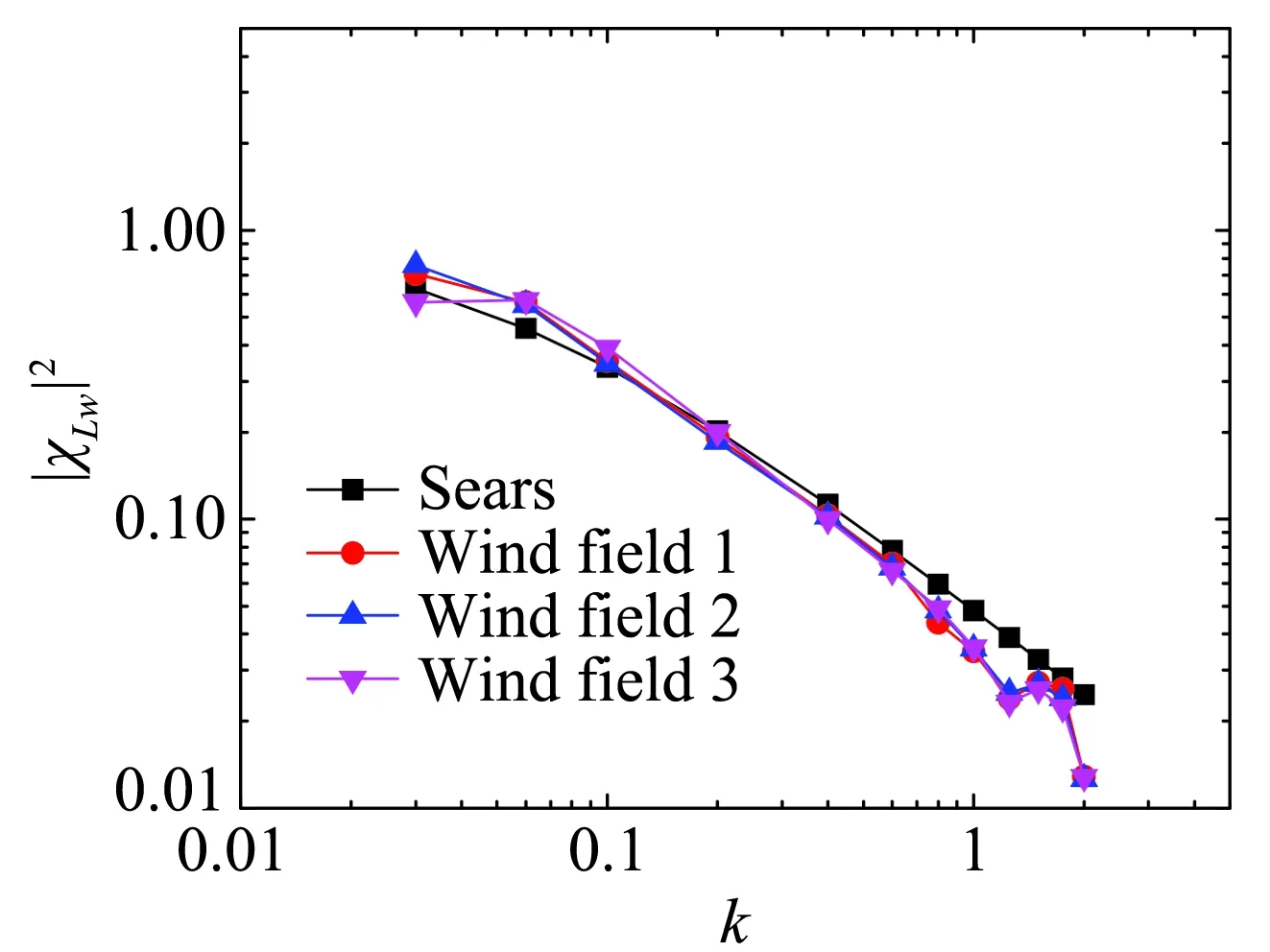
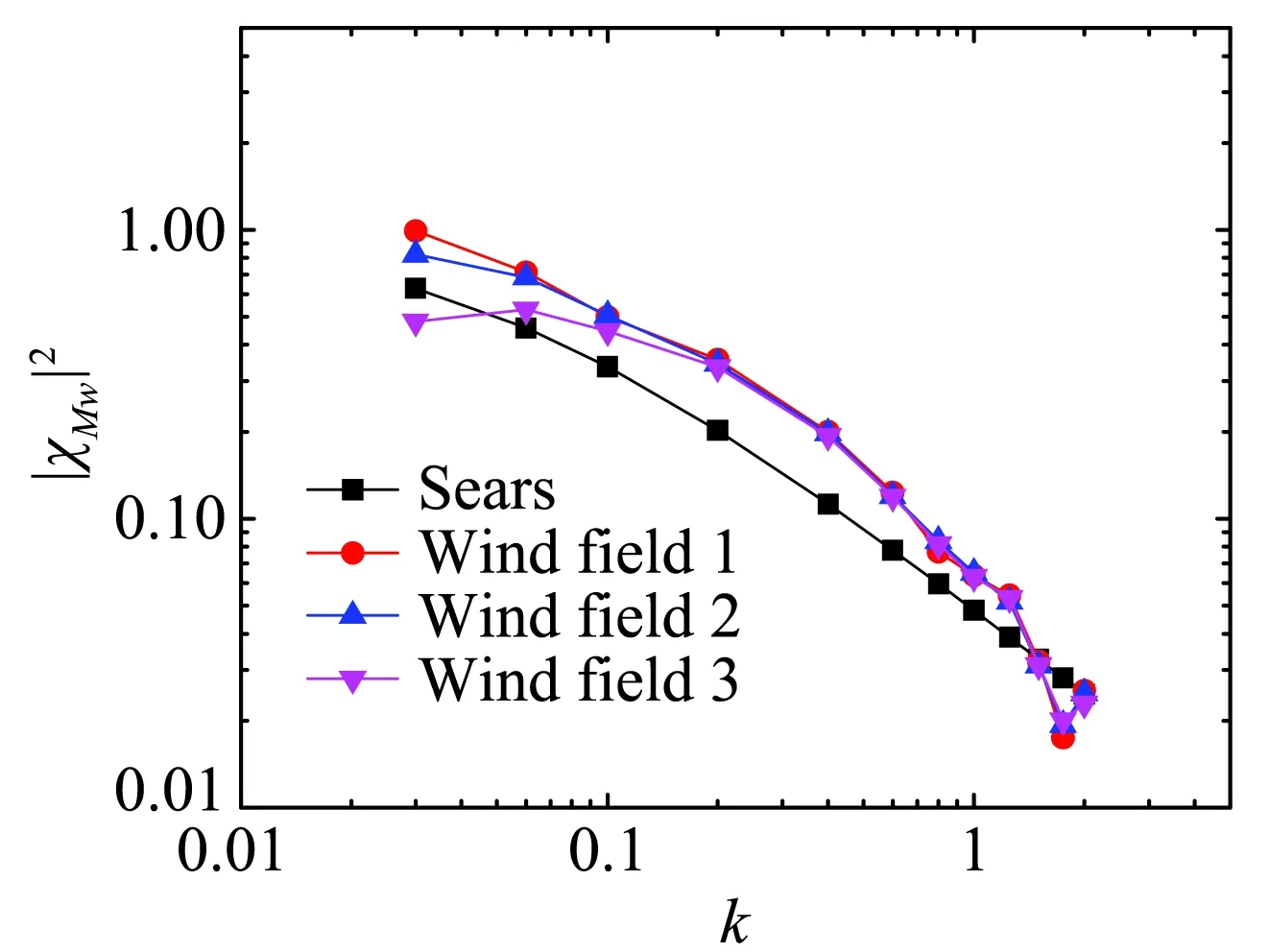
图8、图9分别为平板、流线型箱梁、钝体双边肋断面在不同来流下的升力气动导纳函数和扭矩气动导纳函数。
由图8、图9可以看到,平板与箱梁断面的升力气动导纳、扭矩气动导纳除了在较低折算频率处离散性稍大外,在其它折算频率范围内基本一致,体现了流线型断面对风场不具有依赖性或者具有弱依赖性。相比较之下,钝体双边肋断面在三种来流下的升力气
(a) 平板断面
(b) 箱梁断面

(c) 双边肋断面
动导纳和扭矩气动导纳差别较大,表现出较大的离散性,尤其是在高折算频率范围内,体现了钝体断面对风场的依赖性。表明钝体的气动导纳并不能定性为断面的函数,而是由断面与风场共同决定。这主要是由于钝体断面周围会产生复杂的流动分离与再附现象,会对来流简谐脉动引起的气动力产生干扰。而又由于断面周围流动分离与再附现象与来流特性密切相关[19],因此使得最终识别的气动导纳依赖与来流特性。
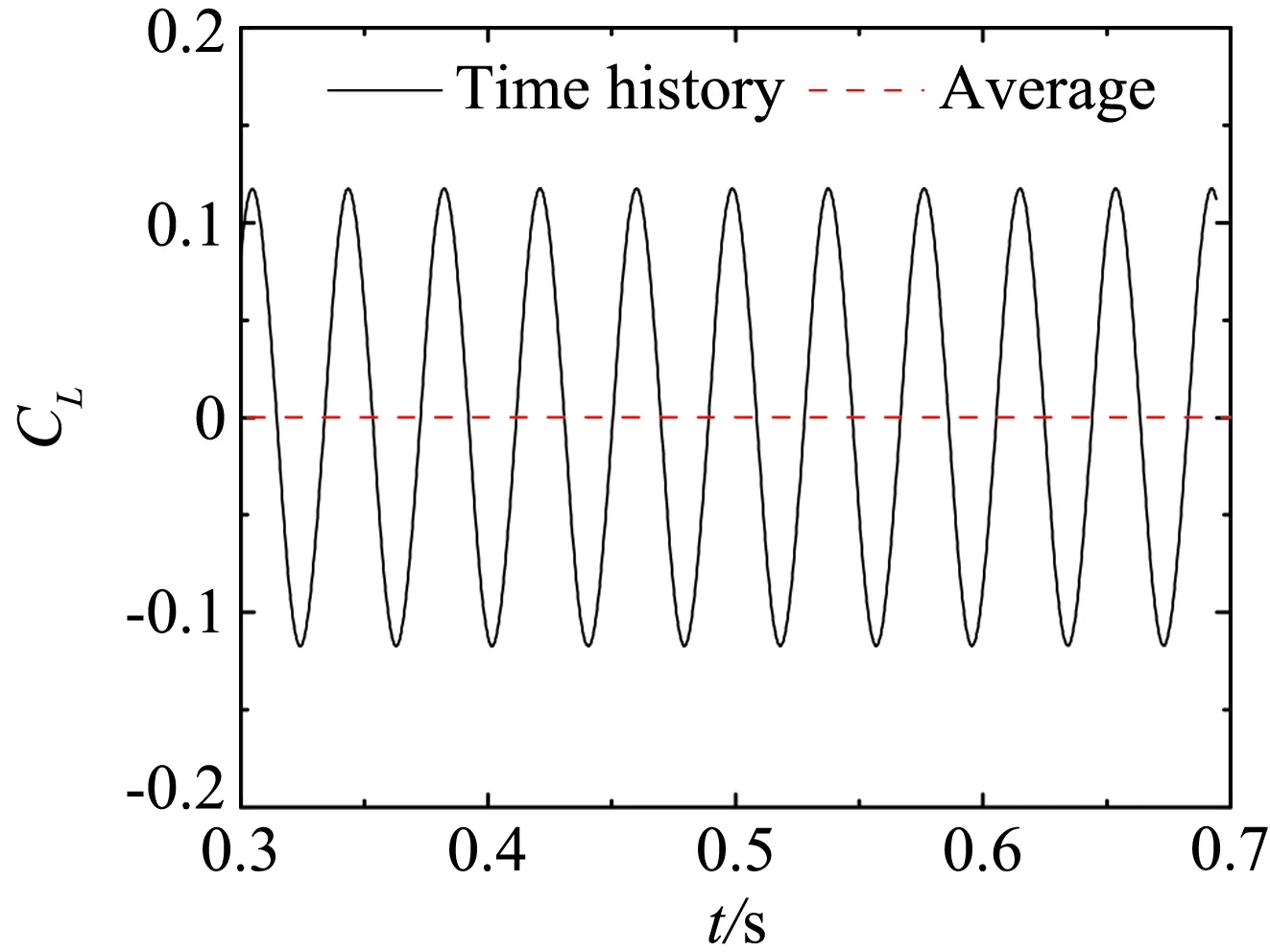
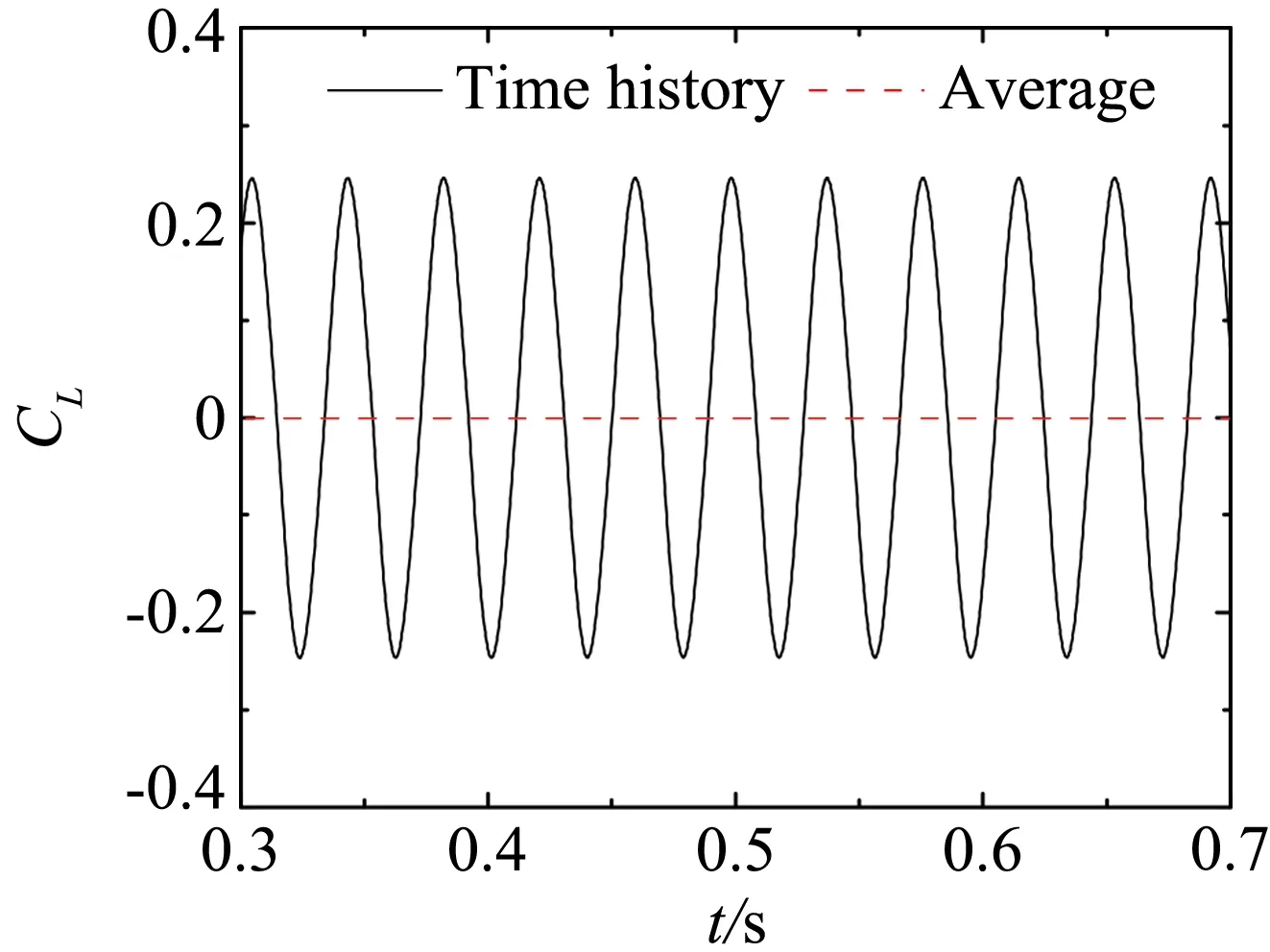
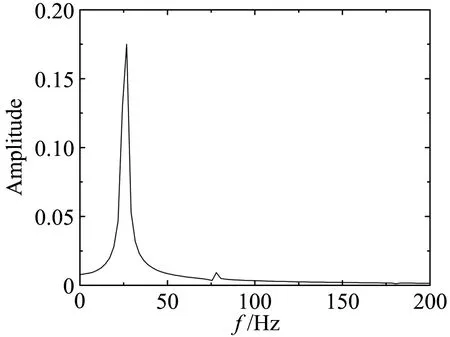
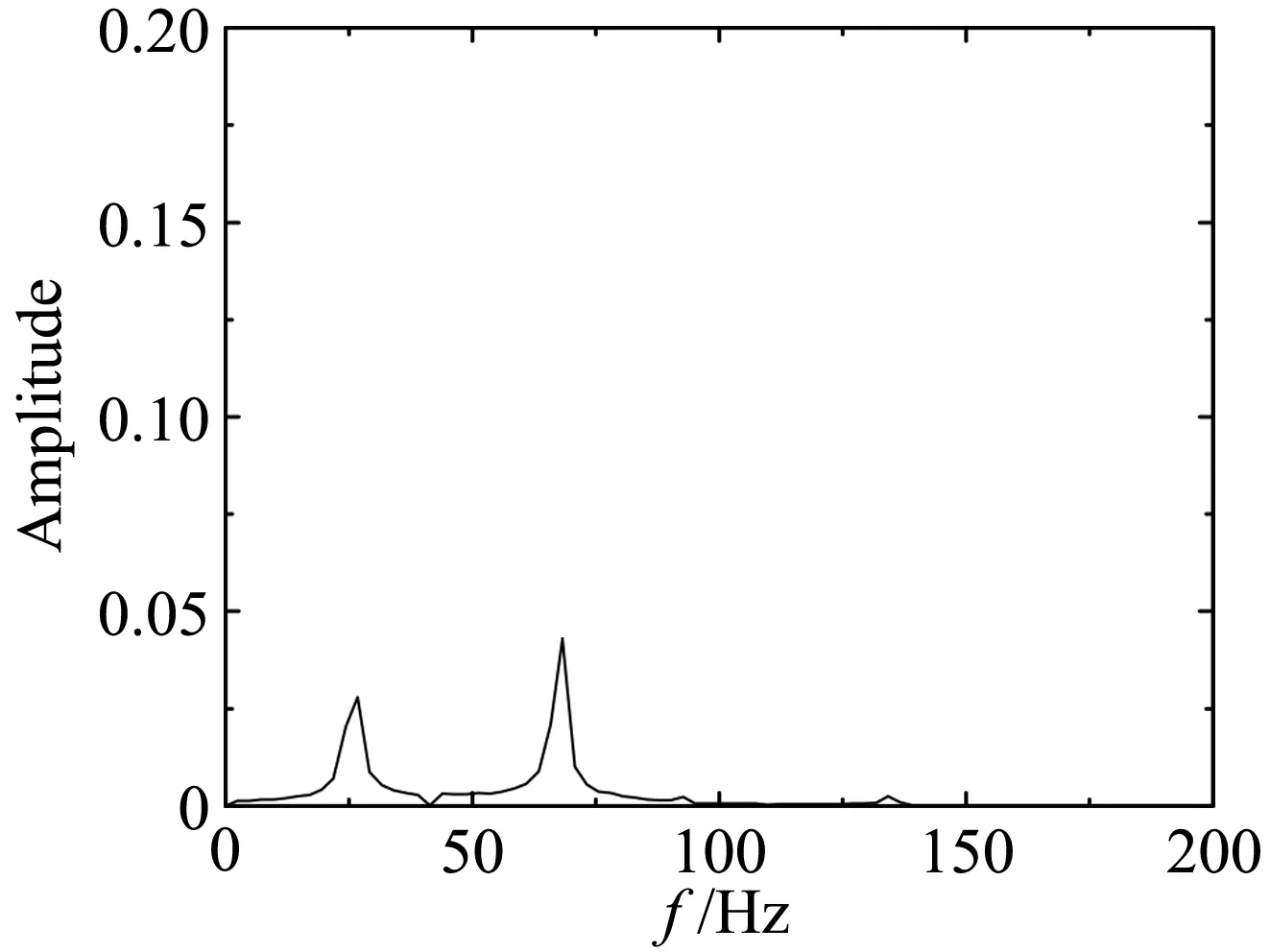
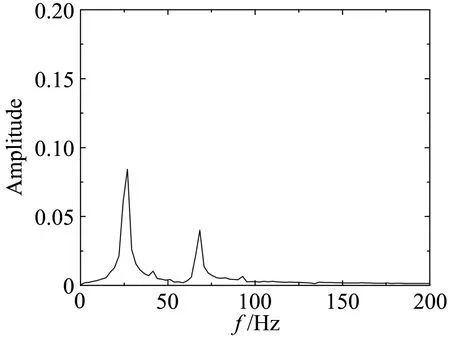
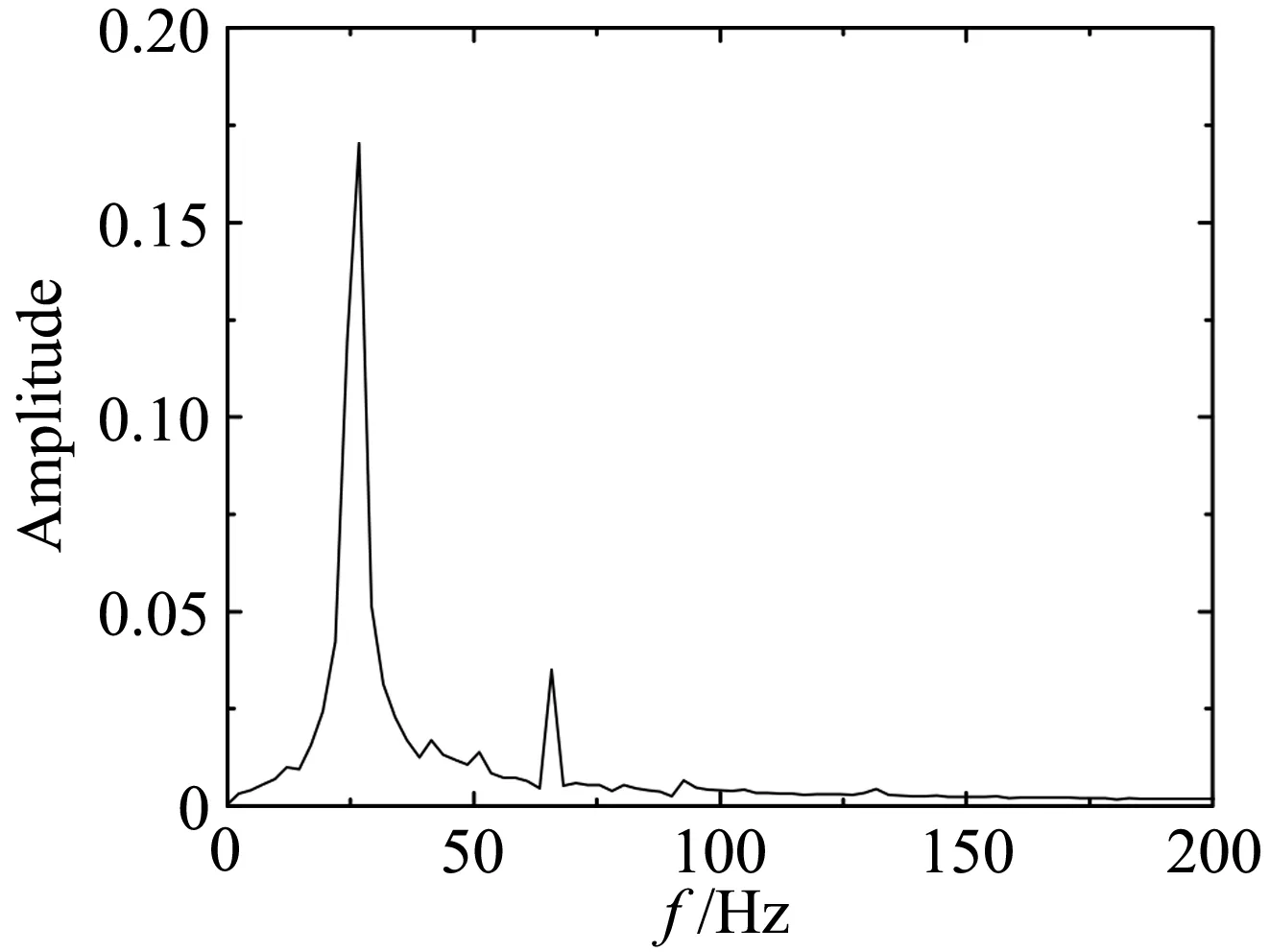
为了进一步说明不同断面形式气动力的差异,作为例子,图10、图11、图12分别给出了平板、箱梁和双边肋断面当k= 0.8时在均匀来流、wind field 1、wind field 2、wind field 3来流下的升力系数时程曲线。图13、图14、图15分别为对应的升力幅谱。其中平板断面因升力为0,所以省略平板断面在均匀来流下的升力系数和升力谱曲线。
(a) 平板断面
(b) 箱梁断面

(c) 双边肋断面

(a) wind field 1
(b) wind field 2
(c) wind field 3
平板断面因其流线性质,升力时程只包含来流简谐脉动引起的气动力,对应的卓越频率为25.82Hz。箱梁断面的尾部会产生周期性的旋涡脱落,从图14可知,在均匀来流下因旋涡脱落引起的升力脉动的频率为66.4 Hz。双边肋断面的几何外形复杂,在它周围的流动现象也更为复杂。从图15可知,双边肋断面的升力时程信号包含有四个显著的峰值,对应的频率分别为:f1=13.4Hz、f2=28.1Hz、f3=41.5Hz、f4=56.2 Hz。从图15也可以看到,频率f2因与来流的脉动频率(25.82 Hz)接近,因此按频率f2脱落的旋涡诱导的气动力会对来流简谐脉动引起的气动力产生干扰,从而使该频率处对应的气动力不再满足叠加原理。
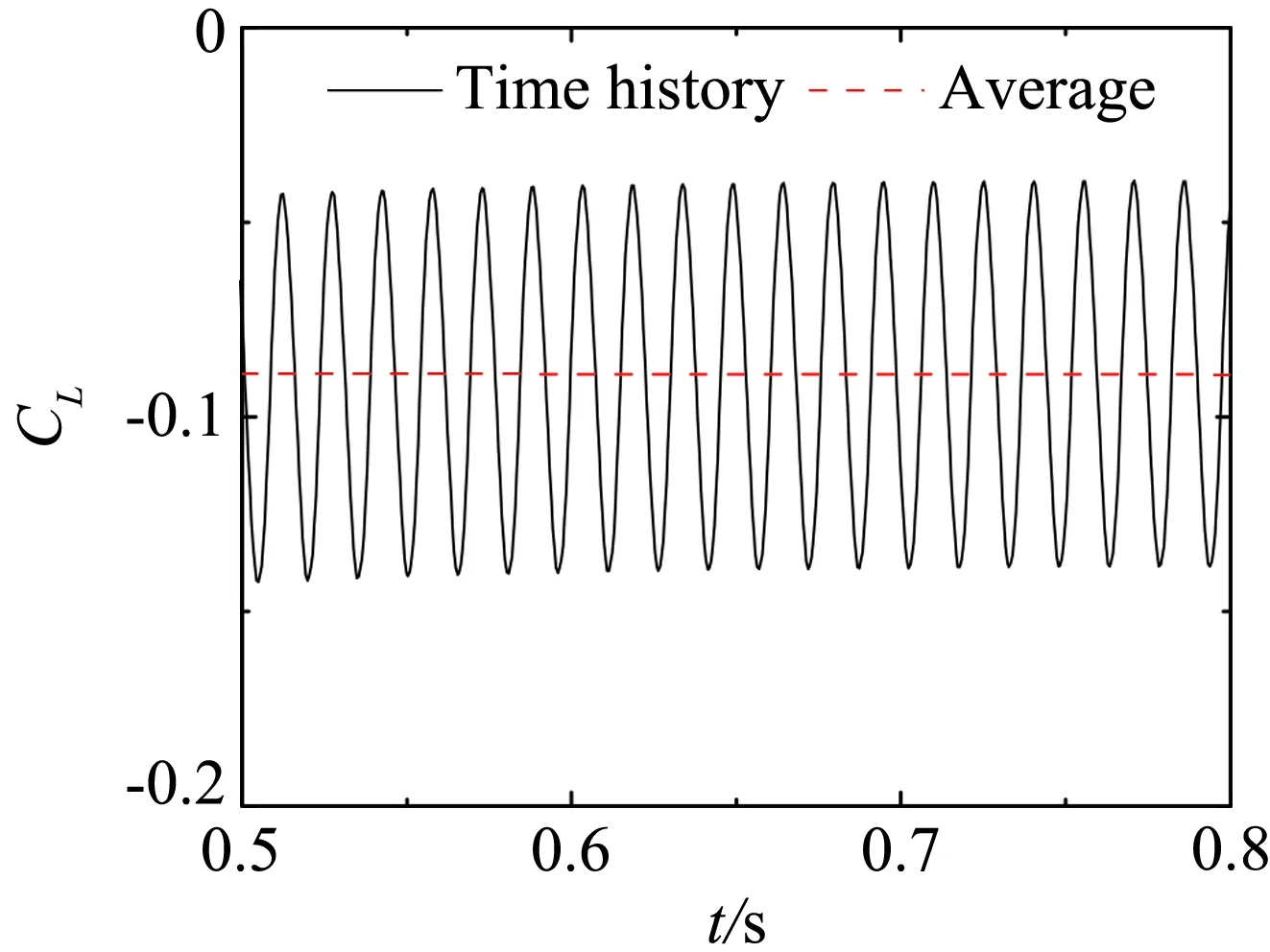
(a) uniform flow
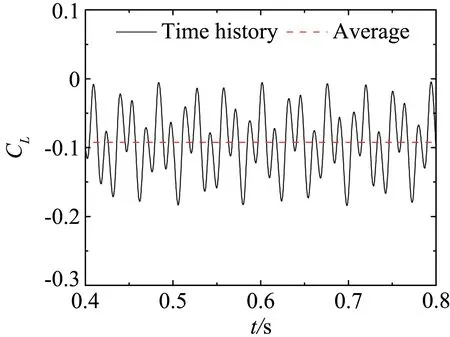
(b) wind field 1
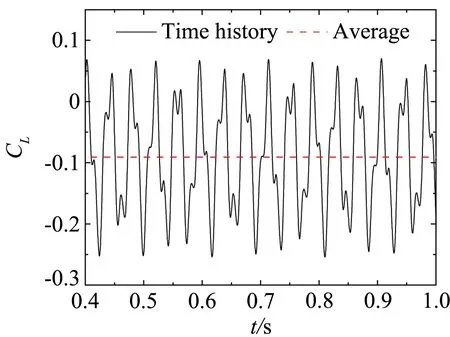
(c) wind field 2
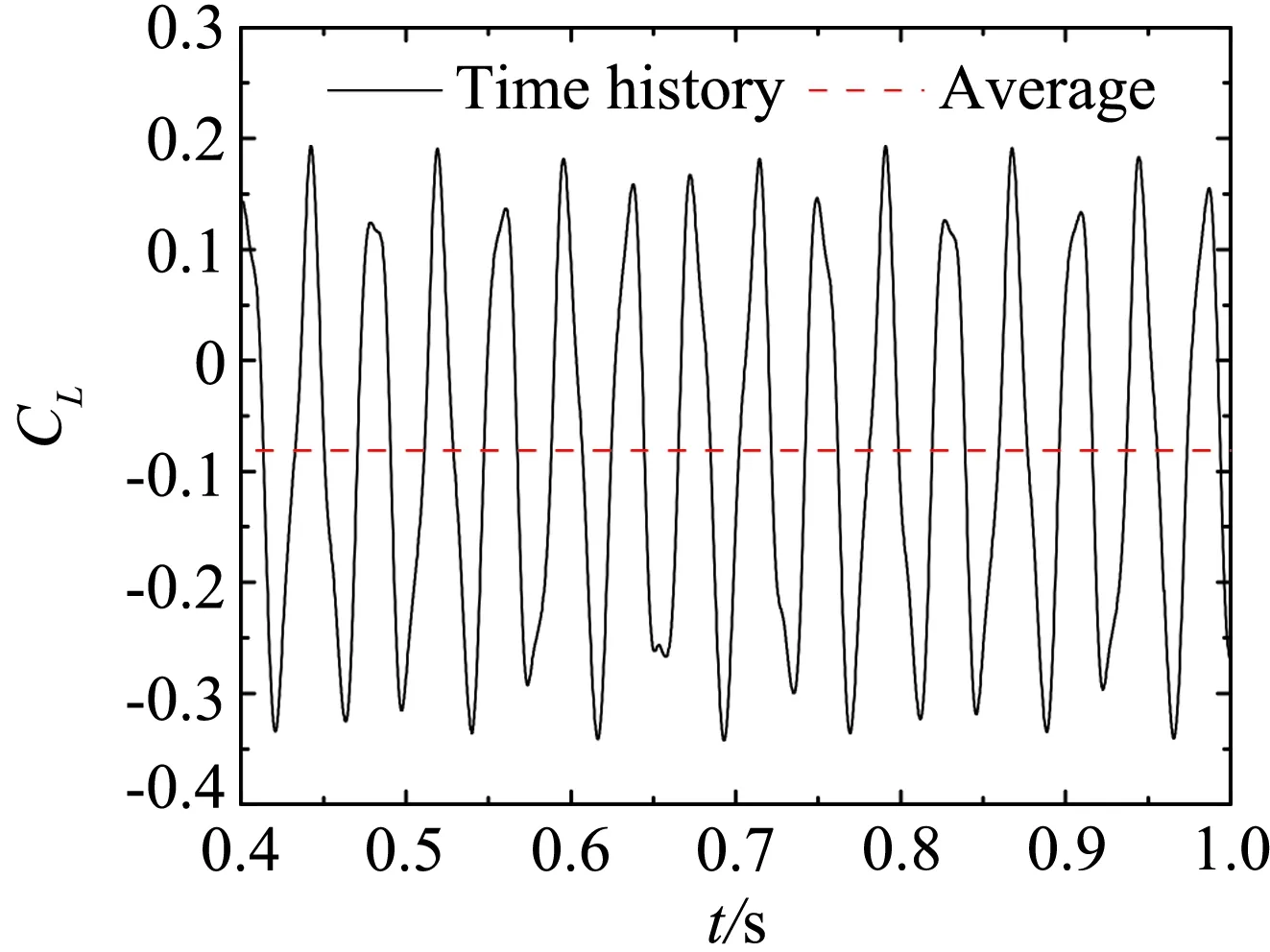
(d) wind field 3
表2为三种断面在来流下升力幅谱及升力幅谱与来流脉动幅值的比值。从表2可以看出平板以及箱梁断面升力时程的幅谱与来流脉动幅值的比值在三种来流中非常接近。这说明流线型断面的气动导纳与来流的脉动幅值无关,仅是断面及无量纲折算频率的函数。相反,具有显著分离流的钝体双边肋断面,断面周围不同尺度的涡诱导的气动力会对来流简谐脉动产生的气动力产生干扰效应。从表2可以看到双边肋断面在不同来流下升力时程的幅谱与来流脉动幅值的比值差别非常大,分别为0.4217、0.3120和0.146。双边肋断面对来流风场的依耐性,表明钝体断面的气动导纳并不能定性为断面的函数,而是由断面与来流风场特性共同决定的。

(a) uniform flow
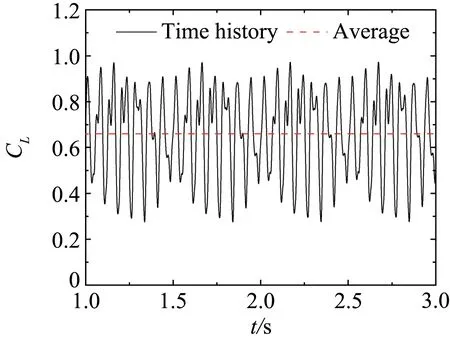
(b) wind field 1

(c) wind field 2
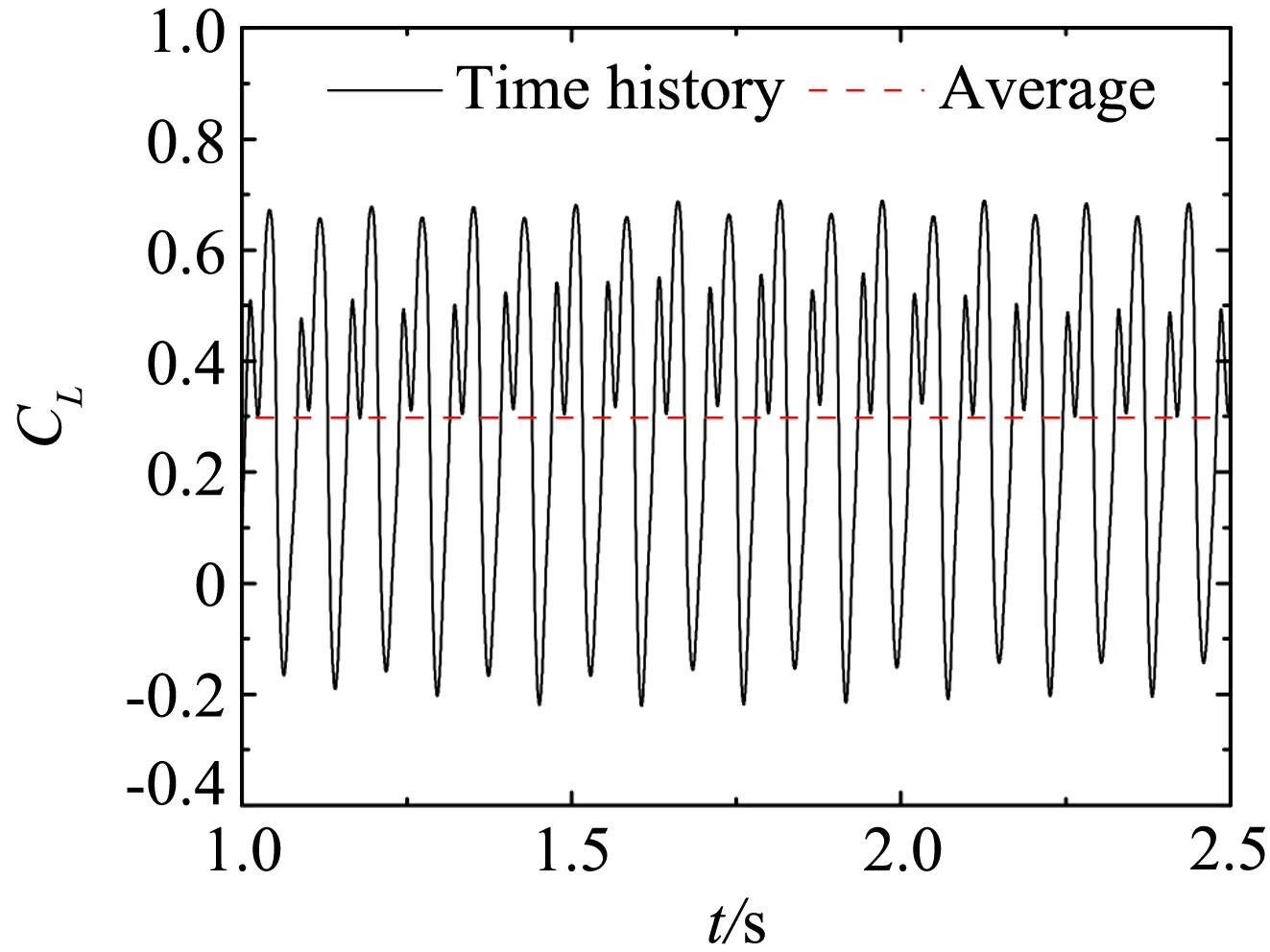
(d) wind field 3
此外,值得一提的是,从图12可以看出,对于双边肋断面不同性质的脉动风对平均气动力特性有着重要的影响,表现为随着脉动风幅值的增加,平均升力显著降低。这一现象与Bearman对垂直与流向放置的平板的平均阻力的研究结果类似[22]。迄今为止,很多研究者对来流湍流度对钝体断面平均气动力
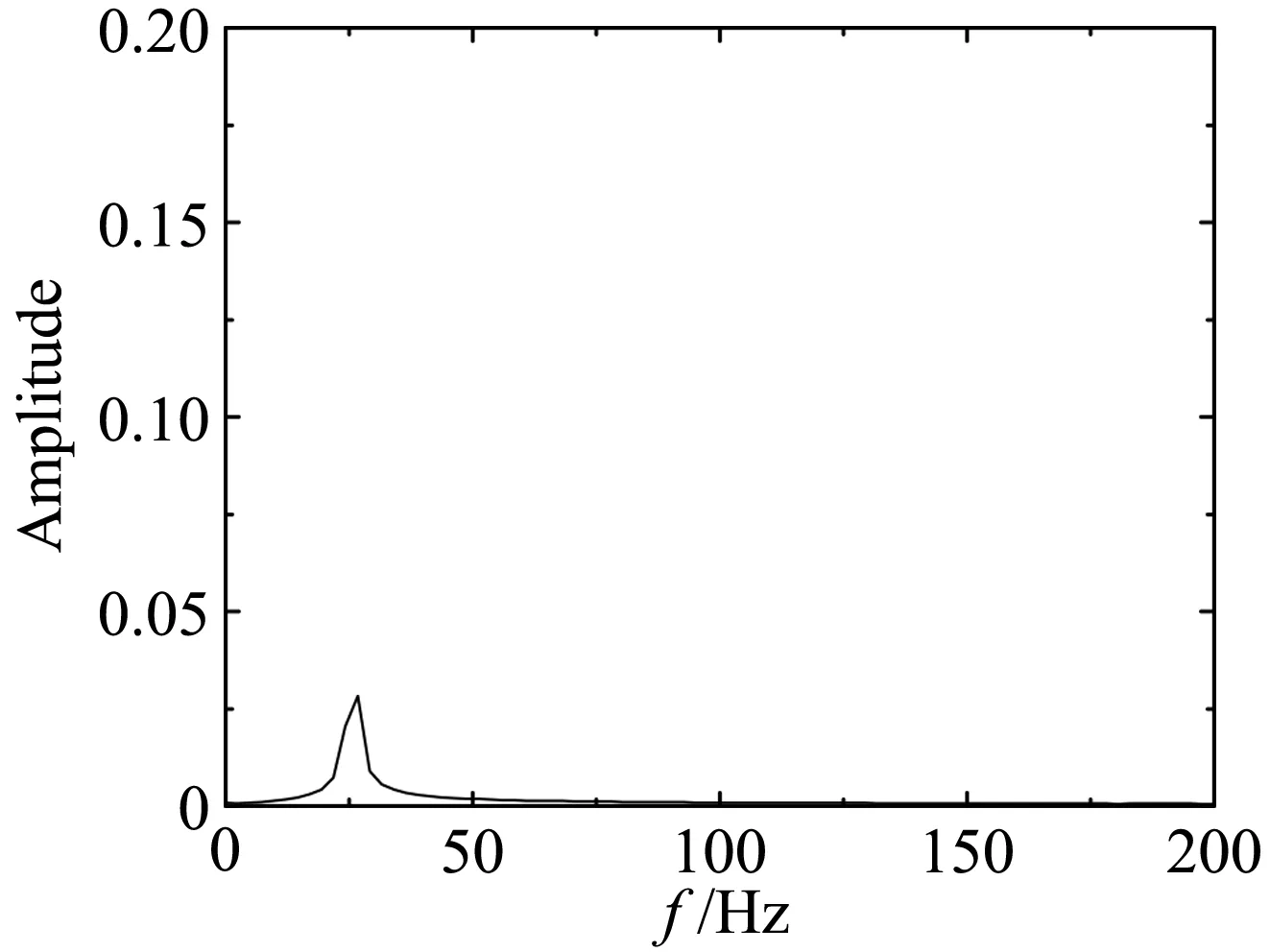
(a) wind field 1
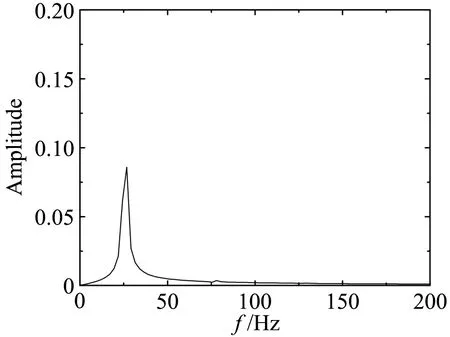
(b) wind field 2
(c) wind field 3

(a) uniform flow
(b) wind field 1
(c) wind field 2
(d) wind field 3
的影响进行了较为深入的研究[21-23]。其中,Bearman认为,这种现象本质上来源于来流湍流对边界层分离后的剪切层及其剪切层再附的影响。
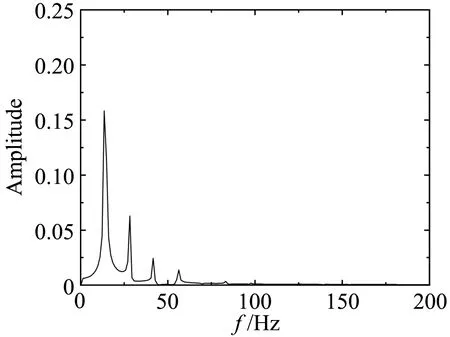
(a) uniform flow
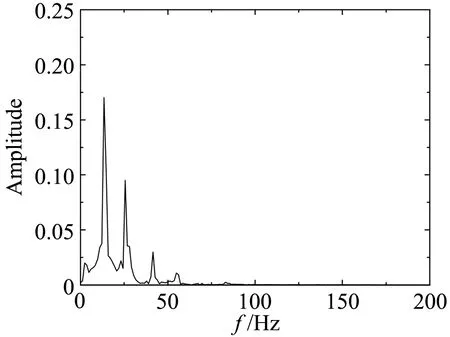
(b) wind field 1
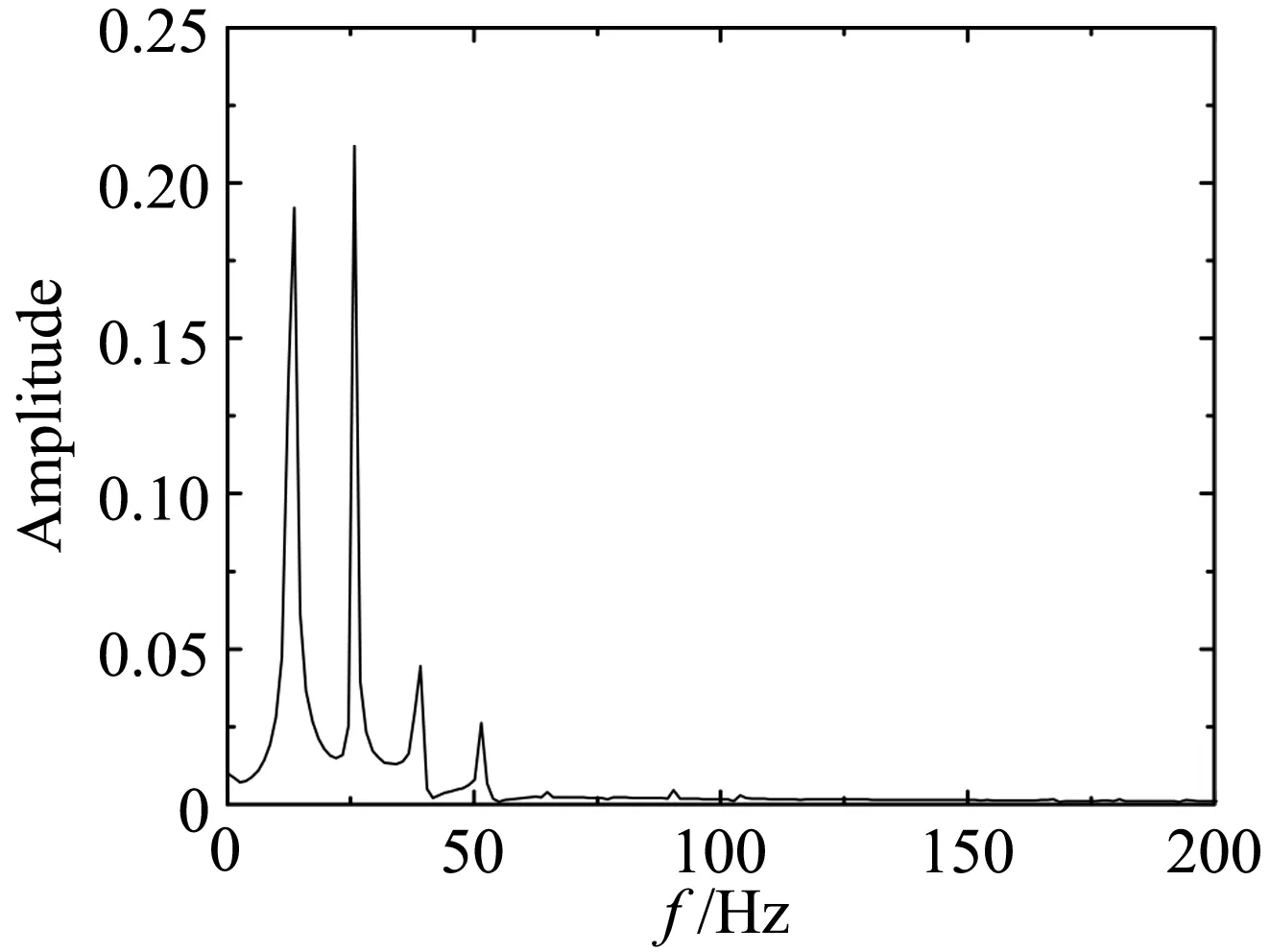
(c) wind field 2

(d) wind field 3

图15 双边肋断面升力系数幅谱Fig.15 Amplitudespectra of lift coefficients for the double-girder section
4 结 论
基于二维非定常RANS模型,计算了三种不同流线程度的断面在简谐脉动来流和宽频湍流下的气动导纳函数,在此基础上研究了不同来流特性对给定断面的气动导纳的影响。根据本文数值计算结果可得出以下结论:
1) 在竖向简谐脉动来流情况下,平板断面的气动导纳与Sears函数吻合良好,表明了在两种不同形式的来流下,本文数值模型及数值方法的可行性。相比之下,湍流作用下,计算所得的气动导纳函数具有很强的随机跳跃性,与薄平板断面的理论解之间有实质性的差异。
2) 本文计算的平板与箱形断面的气动导纳函数均接近流线体断面的特性,即对风场不具有依赖性或弱依赖性,不同风场形成的差异在数值模型的不确定性范围内;相比之下双边肋钝体断面的气动导纳表现出明显的风场依赖性,表明钝体的气动导纳并不能定性为断面的函数,而是由断面与风场共同决定。
3) 双边肋断面的升力系数计算结果表明,不同性质的脉动风对平均气动力特性有着重要的影响,在本文中表现为随着脉动风幅值的增加,平均升力显著降低。这一现象与Bearman对垂直于流向放置的平板的平均阻力的研究结果类似[22],本质上来源于湍流特性对边界层的发展以及平均风场的影响。
