顾及声线入射角的水下定位随机模型
2018-09-28王振杰刘慧敏
赵 爽,王振杰,2,刘慧敏
1. 中国石油大学(华东)地球科学与技术学院,山东 青岛 266580; 2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东 青岛 266071
随着国家海洋战略的逐步推进,海上石油勘探、海底地质探测、海洋工程建设等涉海活动蓬勃发展,需要获取大范围、准确的海洋空间与环境数据,水下声学定位技术是重要基础和保障[1]。
高精度的水下定位必须采用正确的随机模型。目前对于水下定位观测量的随机模型大多采用等权模型,认为各观测量的先验方差相等,模型实现简单,但与实际不符,影响水下定位精度。与之相比,在卫星定位方面,国内外学者对随机模型进行了广泛研究,先后提出了高度角随机模型[2]、信噪比随机模型[3]、最小范数二次无偏估计(minimum norm quadratic unbiased estimation,MINQUE)模型及其简化形式[4]。文献[5]采用超短基线观测数据对高度角随机模型和载噪比随机模型的系数进行了修正;文献[6—8]中GPS定位随机模型考虑了观测值精度、时间相关性、交叉相关性等的影响;文献[9]提出了一种基于移动窗口实时估计双差观测值先验协方差阵的方法,改善了动态定位结果;文献[10]提出了一种基于最小二乘残差序列的实时随机模型估计方法,改善了基线解算结果。上述随机模型估计方法在GNSS定位领域应用广泛且效果显著。在水下定位方面,通常将水下声学测距观测视为独立等精度观测[11],但在实际的水下定位中,随声线入射角增大,声信号传播路径增加,声速误差和声线弯曲影响显著[12-13]。目前对于水下声学定位随机模型的研究还不多见。
本文针对走航式水下声学定位方式,首先介绍几何法水声定位函数模型,并从参数估计和方差估计的角度对随机模型不完善的影响进行分析,然后结合水下定位实际,顾及水声测量误差和声线弯曲误差影响,构建了基于声线入射角的水下定位随机模型,并通过模拟算例和实测数据对新模型的有效性予以验证。
1 随机模型不完善影响规律分析
1.1 几何法水下定位函数模型
如图1所示,假设ti(i=1,2,…,n)时刻由GPS给出的测量船的位置为xi(xi,yi,zi),海底应答器的坐标为xo(xo,yo,zo),测得的测量船至
应答器的距离(传播时间乘以声速)为ρsio,则有
ρsio=f(xo,xi)+δρdsio+δρvsio+εio
(1)
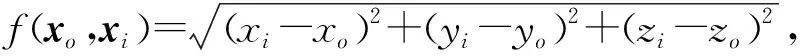

图1 走航式水下声学定位示意图Fig.1 The sketch map of underwater acoustic positioning by surveying ship
观测方程线性化得

εio+bsioεxsi
(2)
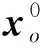
获取3个及以上观测历元的数据后,观测方程可以统一表达为
l=Adx+εl
(3)
式中,l为常数项;A为观测方程系数矩阵;εl为观测过程中的偶然误差及与声速、传播时间有关的系统误差的综合误差项。


式中
在不考虑系统误差影响的前提下,误差方程可写为
V=Adx-l
(4)
法方程为
ATPAdx-ATPl=0
(5)
1.2 随机模型不完善对参数估计的影响
随机模型如下式
(6)

(7)
随机模型不完善可归结为定权不正确[15]。设定权不按式(6),而是将权定为q。假设水下定位函数模型正确、参数选取合适,下面从参数估计和方差估计两方面分析随机模型不完善的影响。
1.2.1 参数估计的最优无偏性影响分析
令M=ATqA,最小二乘平差解可表示为
Xq=M-1ATql
(8)
Xq的真误差及数学期望分别为
(9)
(10)
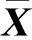
结合式(8),Xq的方差为
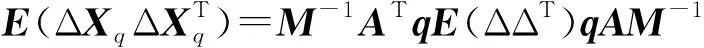
(11)
令P-1=hTh、S=hqAM-1,则
(12)
令R=ATh-1,则
RS=ATh-1hqAM-1=I
(13)
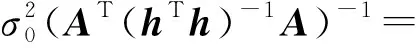
(14)
根据矩阵型施瓦茨不等式,即
BTB≥(AB)T(AAT)-1(AB)
(15)
可得

(16)
当S=RT(RRT)-1RS,即q=P时等号成立。由式(14)可知,定权不正确将影响估计量的最优性,且只有定权正确时才可得到最优估值。
1.2.2 单位权方差估计的无偏性影响分析
定权为q,则有
Vq=AM-1ATql-l
(17)
(18)

(19)
当定权正确,即q=P时
(20)
(21)

综上,随机模型不完善不会影响坐标解算的无偏性,但会影响和方差估计的无偏性。当且仅当定权正确,才可得到坐标最优估值和单位权方差的无偏估值。因此,高精度水下定位应该采用正确的随机模型。
2 基于声线入射角的随机模型

在实际的水下声学定位中,目标距离通过声波在水中传播时间的测量获得,时间测量和声速剖面测量的精度直接影响到距离测量的精度,因此测距误差主要是由测时误差和声速测量误差引起的[16]。
借助于高精度的信号检测技术和时延估计方法,在作用距离覆盖范围内测时能够达到优于0.1 ms的精度要求。但持续走航作业的特点决定了测量船在发射声信号时和收到反馈声信号时的坐标并非严格相同即存在位置差[17],在距离(时间乘以声速)交会定位中可视为存在一定的等效测时误差,该误差可通过对测量船位置进行插值予以削弱。对同一应答器而言,大声线入射角对应的声传播路径大,声传播时间长,在船速变化不大的情况下,故船的位置差异大,可视为测时误差增加。
水中声速受环境因素影响表现为深度、温度、盐度的综合函数,且存在空变性和时变性。声速测量误差引起的测距误差是声速测量误差在整个声传播过程中的积分,可以将声速误差看作是距离变化的函数[18-19]。声速误差及由此产生的测距误差近似呈线性关系,声速误差越大,测距误差显著。随声线入射角增大,声程增加,声速误差对测距影响增大[20]。
此外,声波在海水中传播,会在介质常数不同的两个界面上产生反射、折射和某种程度的反向散射,从而导致波束声线弯曲和传播速度发生改变,声速变化越大,弯曲越显著[21-22]。100 m水深的情况下,声线弯曲最大可以达到1.7 m,声线与平均声速距离的差值最大可以达到5 m(文献[23])。在水下定位中,由于声线弯曲引起的水平距离误差随声线入射角的增大而增大,高程误差在声线入射角大于45°时随声线入射角的增大而增大[24]。
针对走航式水下声学定位方式,对于同一目标应答器而言,测量船换能器收发的大入射角声信号受声速测量误差和声线弯曲影响更为显著,因而测距精度比小入射角的要低,据此对观测值进行赋权。基于声线入射角的随机模型,其本质是利用数据观测的附加信息来评定观测数据的质量(图2)。

图2 声线入射角示意图Fig.2 The sketch map of sound ray incidence angle


(22)
考虑到水下定位实际,可认为声线入射角越大,观测量先验方差越大。结合对水下定位测距误差的分析,基于观测量入射角和先验方差之间存在正相关的定性关系,尝试探索构建更符合水下定位实际的随机模型。从数学角度看,选取最具有代表性的一般比例函数、三角函数和指数函数这3类相关函数,构造4种声线入射角随机模型。4种随机模型分别基于一般正比函数、入射角余弦函数、入射角指数函数和入射角分段余弦函数。具体表达形式如下:
(1) 一般正比函数
(23)
(2) 入射角余弦函数
(24)
(3) 入射角指数函数
(25)
(4) 入射角分段余弦函数
(26)
式中,s0、a0、a1为常数;k1、k2、k3、k4为比例系数(量级调节因子);θ0为设定的入射角阈值,根据关于声线弯曲误差影响研究结果可设为40°~50°(文献[24])。根据调研结果,声线入射角取值范围可认为是0°~87°,可确定出对应相关函数取值范围,为便于研究,权值可归一化到0~1,据此可以反算出各系数取值范围。常数s0、a0取0.1~1.0,系数a1取-1.0,系数k1取0.01,其余比例系数取1.0。
水下应答器对应的各历元观测量的方差阵为
(27)
则观测量的权矩阵为

(28)
结合式(4),应答器位置改正数及观测值改正数可由下式求得
(29)
验后单位权中误差、平差参数X的协方差阵
(30)
式中,r为多余观测数;t为必要观测数,一般为3;QXX为平差参数的协因数阵。
3 算例分析
3.1 仿真算例分析
模拟海上石油勘探OBC(ocean bottom cable,海底电缆)声学二次定位[26-27]数据采集过程。模拟对称双测线走航观测水下100 m处应答器列,相邻应答器间距50 m。声速剖面采用Munk理想声速剖面,表层声速为1548 m/s,采用分层等梯度射线声学跟踪算法仿真传播时间,具体方法参考文献[28]。模拟水面波高为2 m的余弦波动。假设船速为3 kn/h,采样间隔为4 s。偶然误差参考文献[11],假设换能器定位中误差各方向为10 cm,测距误差设为0.3%倍的斜距(图3、图4)。

图3 船迹及应答器位置示意图Fig.3 The sketch map of ship track and the transponder
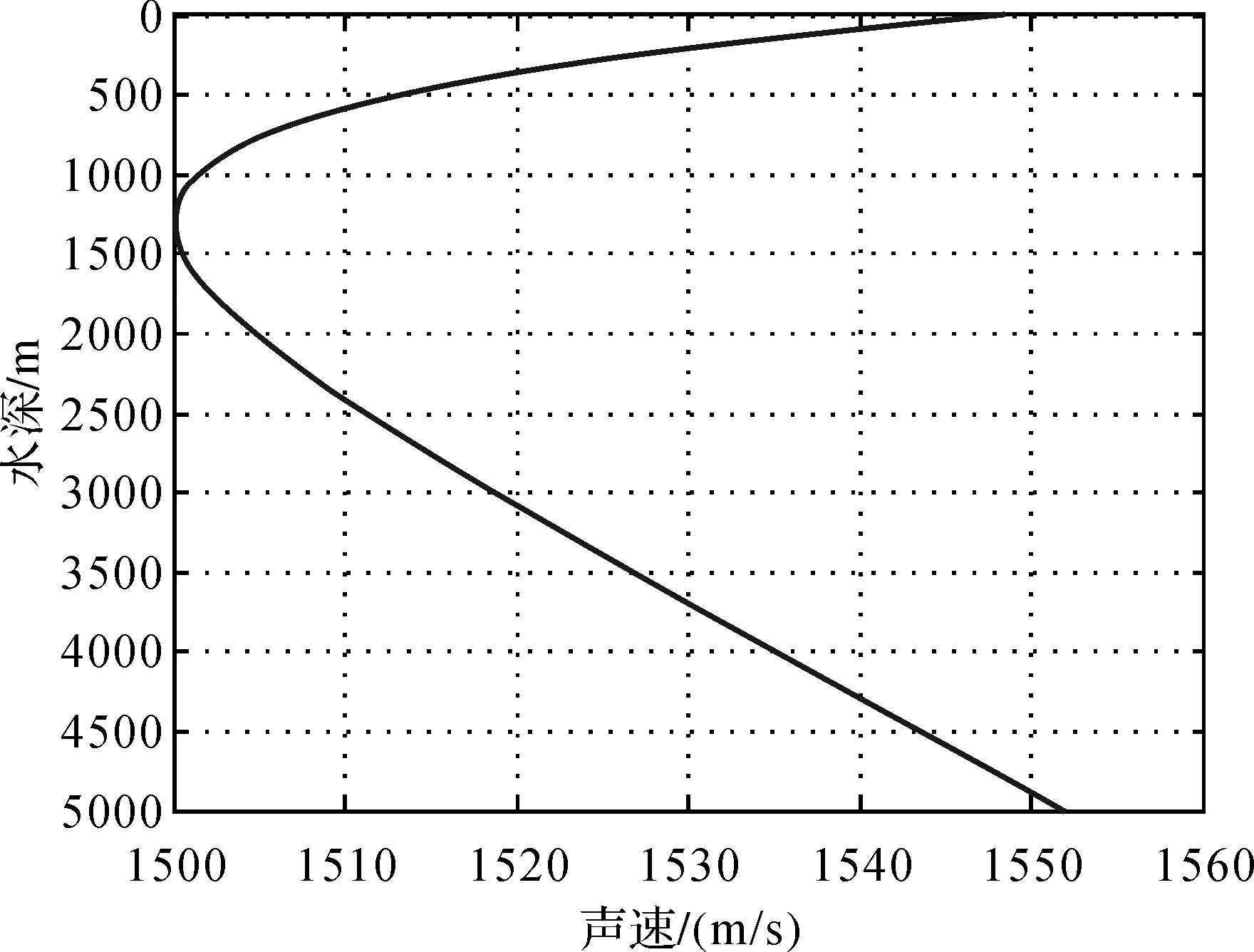
图4 Munk理想声速剖面Fig.4 The ideal Munk sound speed profile
计算测量船按设计测线走航在不同观测历元下的声线入射角,如图5所示。综合6个应答器,各历元平均声线入射角为55.18°,最大声线入射角为78.73°,最小声线入射角为26.36°。
选择余弦分段函数的入射角随机模型,采用不同声线入射角阈值θ0,定位解算结果如图6所示。考虑到模拟数据质量引起的解算结果微弱“震荡”,故通过拟合进行提炼其趋势规律。拟合结果表明,声线入射角阈值θ0取值在40°~50°范围内时,分段余弦随机模型的几何法水下定位结果最优。

图5 不同观测历元下声线入射角Fig.5 Sound ray incidence angle of different epochs

图6 不同声线入射角阈值对应的余弦分段模型定位RMS值Fig.6 The RMS result corresponding to the IASM of cosine piecewise function with different incidence angle threshold
根据设计方案,模拟走航试验500次,分别用一般等权随机模型和4种不同的入射角随机模型的几何法进行定位解算。
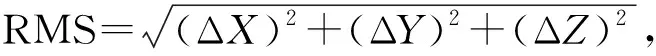
统计不同基于入射角的定权方案下权值分布的标准差,4种方案依次为0.034 9、0.234 1、0.226 6和0.287 6。由图7可知,模拟试验结果表明,入射角随机模型和等权随机模型下的几何法定位解算RMS值明显“分层”,前者定位结果优于后者。以往的等权随机模型,几何法定位RMS值为0.411 m;4种基于入射角定权的随机模型(一般正比、余弦函数、指数函数和分段余弦函数),几何法定位RMS值分别为:0.292 m、0.294 m、0.317 m和0.242 m。其中,分段余弦函数在阈值θ0的前后采用不同的分母因子,因而权值会存在一个跳跃导致权值分层,分层后的权值数据增加了其标准差,离散程度较其他方案更为显著。直观上,受误差影响大的观测值权重相对要更小一些,即对较大入射角进一步降权,削弱了声线弯曲对定位解算的影响,具有一定的有效性。
3.2 实测数据分析
实测数据采用南海试验数据。本次试验时间为2016年10月24日至2016年11月7日,试验地点在南海海域(20°44′N,113°28′E附近),试验搭乘东方物探勘探2号考察船,船上搭载电罗经、星站差分系统、测深仪、声速剖面仪,以及Sonardyne公司的OBC声学定位系统和国产BPS声学定位系统。系统主要包括主控机、编码器、换能器、应答器、收放器等。测区水深接近100 m,本试验将OBC和BPS的应答器器捆绑在一起(如图8),进行绝对定位的互检校。

图7 4种随机模型下几何法定位解算RMS值Fig.7 The under water geometric positioning RMS accuracy by four kinds of IASM

图8 放缆作业中的OBC应答器、BPS应答器及节点Fig.8 The OBC,BPS transponders and cables during the manipulation of cable laying
本试验作业流程概述如下:
(1) 测量船离陆地较远,试验采用基于通信卫星的星站全球定位系统(定位精度30 cm左右)和电罗经数据沿指定测线进行放缆作业,缆绳上每隔50 m依次钩挂检波器和应答器。
(2) 放缆作业完成后,测量船沿已放测线绕圈观测,换能器发出声学测距信号,应答器做出响应,换能器接收响应信号后计算往返的时间。同时,采用CTD声速剖面仪测量测区的声速(图9)。

图9 走航船航迹及应答器平面位置示意图Fig.9 The sketch map of ship track and the transponders
试验中测得的声速与时间相乘得到换能器和应答器之间的距离,利用船在不同的位置对同一个应答器测量得到的多个距离观测值交会出应答器的位置。由于两套系统在试验中被捆绑在一起,理论上的绝对位置应该非常接近,可以通过比较两套系统的坐标差值来判断两种方案解算精度,差值越小,说明定位精度越高。
考虑到观测历元数量及数据质量,选取观测具有代表性的2号(59个观测历元)和18号应答器(27个观测历元),如图9中箭头所示,统计不同观测历元下的声线入射角大小,如图10所示。其中,2号应答器平均声线入射角为60.13°,最大声线入射角为77.63°,最小声线入射角为38.66°;18号应答器平均声线入射角为57.10°,最大声线入射角为78.25°,最小声线入射角为39.73°。

图10 2号和18号应答器不同观测历元下声线入射角Fig.10 Sound ray incidence angle of different epochs of 2 and 18 transponders
为了比较等权随机模型和本文入射角随机模型定位精度,分别采用两种方法对OBC数据和BPS数据进行后处理,其中入射角随机模型采用分段余弦随机模型。顾及到测量实际数据质量和数量,将入射角阈值θ0取为50°。在保证应答器初值精度的前提下,考虑观测值质量,选取2、18、22、26、34号应答器,进行几何法最小二乘解算,统计应答器x、y方向的坐标偏差值及RMS值作为外符合精度。
统计各应答器各种模型下定位解算平均RMS值如表1所示。

表1 不同随机模型下几何法定位平均RMS值
由表1可知,由于测距误差的非线性,一般正比模型入射角随机模型改善效果并不显著,后三者明显改善定位结果。入射角随机模型下几何法解算结果在x方向的定位精度略优于y方向,这是因为测线按照x方向布设,决定了观测向量在y方向的观测结构相对差一些,而且入射角在y方向上的分量变化较x方向变化大,基于入射角的随机模型在y方向上效用较为显著。由表1可知,传统的等权随机模型下几何法解算的定位结果RMS值为1.187 m。本文提出的一般正比、余弦函数、指数函数、分段余弦的声线入射角随机模型下解算RMS值分别为1.193 m、1.064 m、1.053 m、0.991 m,不同程度上改善了等权模型的定位结果,尤其是分段余弦函数的入射角随机模型定位结果最好,在定位精度上比传统等权模型具有优势。实测区域水深约100 m,考虑其声速误差和声线弯曲影响并没有足够显著,基于声线入射角的随机模型其优势不够显著,因而相对传统等权方法改进程度并不大,采用深海数据的验证有待在后续研究中进行。
4 结 论
本文在介绍几何法水下定位原理和分析随机模型不完善误差影响的基础上,结合水下定位实际,构建了基于声线入射角的随机模型,并通过模拟算例和实测数据得到以下结论:
(1) 构建的4种基于声线入射角函数的随机模型,结合水下定位实际,考虑了水声测量误差和声线弯曲误差的影响,比等权模型在定位精度上具有优势。其中,分段余弦函数入射角模型通过设定入射角阈值来对较大入射角的观测量进一步降权,提高了定位的有效性和可靠性。当入射角阈值在40°~50°范围内时,本文模型定位精度最高。
(2) 实测数据处理结果表明,水深100 m以内环境下,传统等权模型定位方法解算RMS值为1.187 m,本文提出的一般正比、余弦函数、指数函数、分段余弦的声线入射角随机模型下解算RMS值分别为1.193 m、1.064 m、1.053 m、0.991 m,不同程度上改善了定位结果。
本文模型考虑了水声观测测量误差及声线弯曲误差,本质上是利用数据观测的附加信息来评定观测数据的质量,改善了水下定位结果,具有一定的应用价值。但是,本文模型没有考虑观测量之间的时间相关性,模型中系数的选择主要依赖经验。模型的完善、深海环境下新方法的验证等问题,有待后续深入研究。
