Roughness height of submerged vegetation in flow based on spatial structure ＊

Wei-jie Wang (王伟杰), Wen-qi Peng (彭文启), Wen-xin Huai (槐文信), Xiao-dong Qu (渠晓东),Fei Dong (董飞), Jian Feng (冯健)

1. State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China

2. Department of Water Environment, China Institute of Water Resources and Hydropower Research, Beijing 100038, China

3. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China

Abstract: The classic hydraulic resistance formulas, such as those in the Darcy–Weisbach methods, perform well in the hydraulic design with the characteristic roughness height ks smaller than the flow depth, which can be linked with the momentum roughness height based on the turbulent boundary-layer theory with the log-law formulation. However, when the roughness scale is of the same order as the flow depth, the traditional log-law formulation cannot provide satisfactory results because the flow structure is complicated and the vortices in different layers are dominated by various principles, such as the Karman streets near the channel bed, the mixing layer near the vegetation top, and a canonical turbulent boundary layer above the vegetation layer. Thus, the distribution of the streamwise velocity in the vegetated flow is a combination of the velocity profile linked with the dominant vortex and shows significant differences as compared with the traditional log-law distribution. This paper proposes a new characteristic roughness height of vegetation kv by linking vegetation attributes, especially the characteristics of the cross section in the flow within the vegetation. The power law resistance formula is derived based on a large amount of experimental data. Results show that the new formula is applicable to shallow flows with vegetation.

Key words: Vegetation, resistance, friction factor, roughness height, spatial structure

Various resistance formulas, such as the Chézy,Manning, and Darcy–Weisbach formulas, are widely used in an open-channelflow in hydraulic engineering[1], in them four forms of resistance coefficients are adopted, namely, the Chézyʼs C, the Manningʼs n, the Nikuradse roughness height ks, and the Darcy–Weisbach friction factor f. The Chézy formula is Ub=C( RSf)1/2, where Ubis the bulk flow velocity, R is the hydraulic radius, and Sfis the energy slope. The Manning formula is Ub=. The relationship between the Nikuradse roughness height ksand the Manningʼs n, which is denoted as, where Pn=0.0474, was proposed by Strickler. The Darcy–Weisbach friction factor is, where g is the gravity acceleration. All resistance coefficients (C,n, ksand f) can be related to one another by the same flow velocity U in a respective case. C, n and ksare dimensional, whereas f is dimensionless.The friction factor as a function of the relative roughness ks/R can be expressed in the power-law form as

where N is a constant.

The flow structure is complicated within the vegetation. Different sizes of vortices were vertically generated in different regions. The von Karman streets are dominant in the zone near the channel bed, the mixing-layer theory is followed near the top of the vegetation and the boundary-layer theory is followed in the zone above the mixing layer to the flow surface.From another point of view, the energy dissipation is mainly dominated by the skin friction in the case of small roughness. The drags of large roughness, such as the vegetation drag, are the main cause of the energy dissipation in the vegetated flow[2-4].

This paper proposes a new characteristic roughness height of vegetation kvbased on a theoretical analysis. Its validity is proven by a large amount of experimental data. Results show that the new formula is applicable to shallow flows with a large-scale roughness, especially in the case of vegetation. When the ratio of the flow depth to the vegetation height for the flow through the submerged vegetation hw/hv＜10, we have a typical large-scale roughness condition,as shown in Fig. 1.

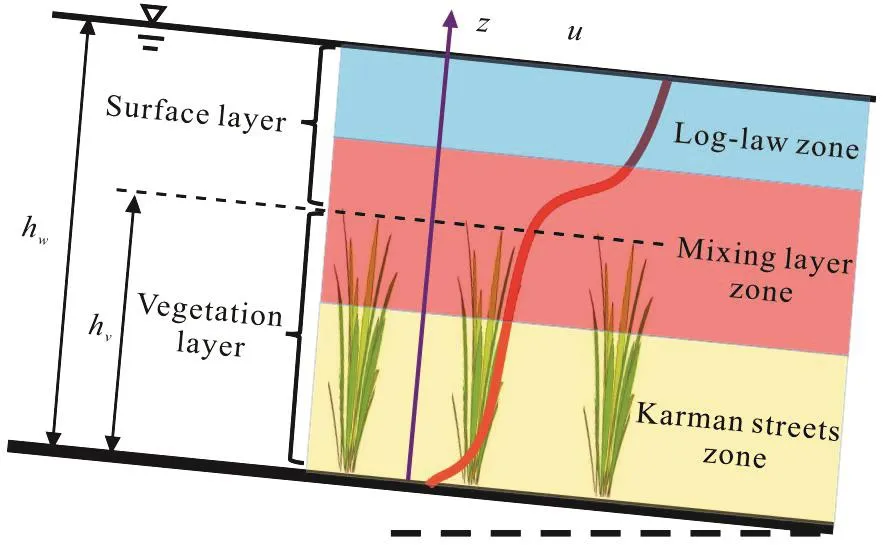
Fig. 1 (Color online) Sketch of flow within submerged vegetation

According to the space occupied by the vegetation or the free water, the flow can be divided into two layers, one of a fast flow in the surface layer (SL)and another of a slow flow in the vegetation layer(VL).

For the layer-averaged velocity in the vegetation layer, a force balance is established between the gravity and the vegetation drag in the steady uniform flow as, the ground friction can always be ignored as compared with the vegetation drag in most cases[5], where ρ is the water density, S0is the bed slope, Cdis the vegetation drag coefficient, m is the vegetation array density (stems per unit ground area) , and D is the frontal width of the vegetation elements. The depth-averaged velocity in the vegetation layer Uvis calculated as[6]

The vertical integration of the velocity distribution formula in the mixing and boundary layers can provide a satisfactory prediction for the layeraveraged velocity in the surface layer.

The hydraulic radius of the vegetated flow is the ratio of the flow volume to the wetted area as R=V/A, proposed by Cheng and Nguyen[7], where V is the volume of water per unit bed area V=hw-φhv, φ the vegetation concentration, which is calculated by φ=mπ D2/4 and the plane area occupied by the vegetation in the channel. A is the effective resistance area, which is dominated by the vegetation drag and is equal to the frontal area per unit bed area A=mDhv, the vegetation-related hydraulic radius Rv=(hw-φhv)/(mDhv)is then obtained.

The vegetation resistance was much investigated from various aspects[8-9]. For the roughness effect on the surface layer, Cheng[10]proposed a length scale as

Here a new roughness height is proposed for the whole flow depth, including the vegetation and surface layers. The characteristic roughness height of the vegetation kvis linked to the height of the vegetation and the arrangement of the vegetation array,which can be expressed as a function of the vegetation height as

where η is the parameter to indicate the blockage of the vegetation array to the flow. The blockage of the vegetation to the flow may be estimated based on the spatial structure, i.e., the ratio of the area of the idealized cross section to that of the actual cross section

where Lspis the spatial averaged distance of adjacent stems, as shown in Fig. 2.

The vegetation drag per unit bed area is τv=. The Darcy–Weisbach formula gives the vegetation-related result as, which is given as

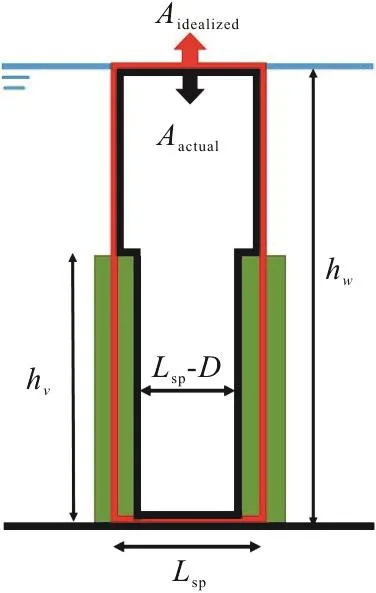
Fig. 2 (Color online) Sketch of blockage of vegetation in flow

The flow is found to follow the quadratic resistance law at very high Reynolds number. The friction factor varies with the relative roughness in power law.The relative roughness can be expressed as kv/Rv,following the power law of resistance similar to the form for the small roughness elements as

where1λ and2λ are the empirical constants determined by experiments.

A total of 301 groups of data were collected for the flow through submerged rigid vegetation[10,11].

The effective width of the canopy layer is B(1-φ), with consideration of the volume occupied by the vegetation. The bulk velocity Ubcan be calculated by the ratio of the discharge Q to the effective cross-sectional area as

The best-fitting of the friction fvfrom 301 groups of collected data gives the empirical parameters λ1=0.8872 and λ2=0.6536, and we have

The correlation coefficient Rcc=0.78 is shown in Fig. 3. The prediction of the bulk flow velocity Ubusing Eqs. (5), (6) is given as

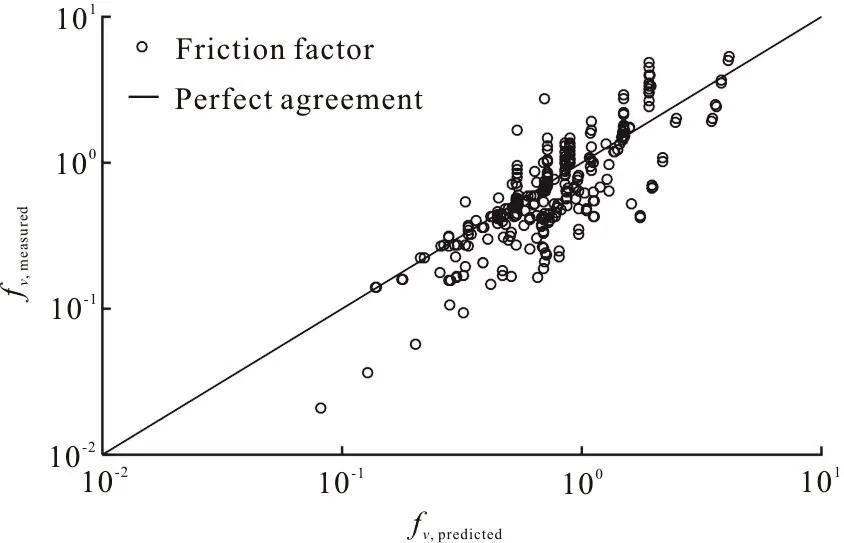
Fig. 3 Comparison between measured and predicted friction factors

It is shown that the correlation coefficient Rcc=0.94 between the measured and predicted bulk velocities, as illustrated in Fig. 4, which proves the validity of the power-law formula (Eq. (6)).

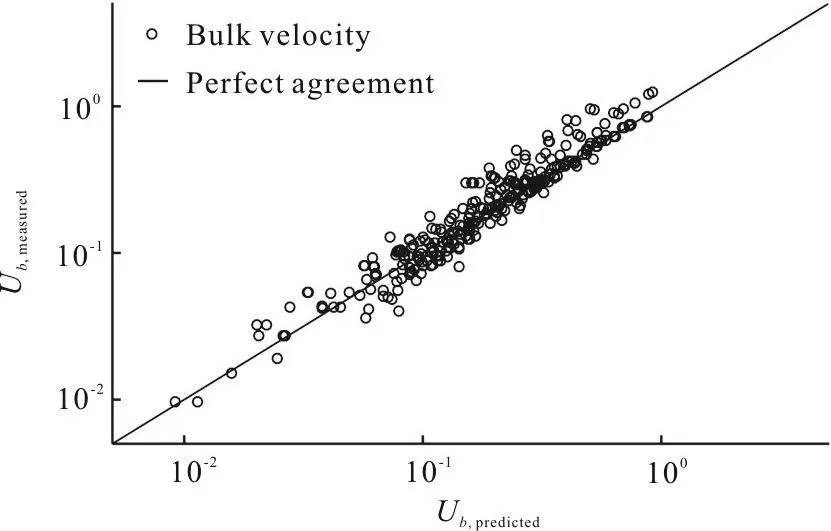
Fig. 4 Comparison between measured and predicted bulk velocities (m/s)

The following conclusions can be drawn: classic Darcy–Weisbach formula performs well when the flow depth is larger than the characteristic roughness height ks, which can be explicitly linked with the momentum roughness height based on the turbulent boundary-layer theory with a log-law formulation.However, the log-law formula cannot provide satisfactory results when the flow depth is comparable to the roughness height, i.e., in the same order of ks,which is referred to as the large-scale roughness.Under this condition, a new characteristic roughness height of vegetation kvis proposed based on a theoretical analysis of the spatial structure. Moreover,the power-law resistance formula is proposed for the vegetated flow, and a large amount of experimental data have proved the validity of the present model,which shows that the new power-law resistance formula is applicable to the shallow flow with vegetation, especially for the prediction of the total flow rate.