新型电液力加载装置的集成设计

,

(1.华中科技大学船舶与海洋工程学院，湖北 武汉 430074；2.高新船舶与深海开发装备协同创新中心，上海 200240；3.船舶和海洋水动力湖北省重点实验室，湖北 武汉 430074)

0 引言

电液力加载装置广泛应用于轴系和舵机的负载模拟以及疲劳试验，对于检验设备性能和提高系统可靠性具有重要意义[1-3]。

传统的电液加载装置多以阀控液压缸为执行元件，控制阀的节流损失使系统整体效率较低。同时，控制阀在进行高频率的压力/流量调节时容易产生高频自激噪声，对系统稳定性造成不良影响[4]。为此，研制了一种基于电动缸的新型电液加载装置，依靠改变封闭油液体积的方式产生加载压力。

该装置作为典型的力伺服系统，其控制性能对系统参数的选取十分敏感。很多情况下，某一组设计参数即使从机械设计的角度上看是最优的，也不能保证在控制角度上获得最优性能[5]。传统的设计方法在处理以上问题时存在一定的局限性，因为其机械和控制的设计过程是相互独立的。为了获得最优的设计结果，在此，提出了同时包含机械和控制参数的加载装置集成设计方法，并通过实验进行验证。

1 系统原理及数学模型

新型电液力加载装置的主要组成部分如图1所示。按照运行工况的不同，该装置的工作原理可从以下4个方面阐明：

图1 新型电液加载装置原理示意

a. 动态加载工况。换向阀1、换向阀2和换向阀3分别处于下位、右位和中位，由工控机控制电动缸的活塞推杆挤压承压筒内部油液以产生期望的油压，推动加载缸活塞实现加载。

b. 保压工况。换向阀1、换向阀2和换向阀3分别处于下位、右位和中位，加载液压缸左腔的油液与外界隔断，保持恒定的压力。

c. 回退工况。换向阀1、换向阀2和换向阀3分别处于上位、左位和左位，油泵输出的低压油注入加载缸右腔使活塞回退至起点。

d. 补油工况。换向阀1、换向阀2和换向阀3分别处于上位、左位和右位，油泵为承压筒以及加载液压缸左腔补充低压油液。

上述4种工况中，动态加载工况是最基础和重要的功能，也包含了最复杂的动态特性。在此，主要基于动态加载工况的要求对其进行建模和分析。

1.1 电动缸模型

电动缸的典型结构如图2所示。其中，活塞推杆是一内径比滚珠丝杆直径稍大的套筒结构，一端与滚珠螺母相连，另一端加装端盖作为活塞杆。滚珠丝杆转动时，直线导轨通过滚珠螺母上的键槽限制活塞推杆的转动。

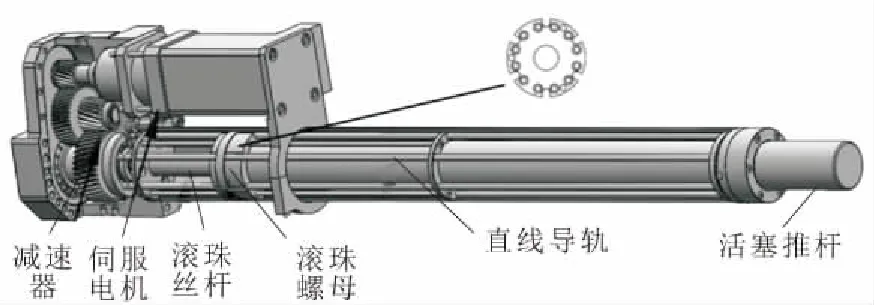
图2 电动缸的一种典型结构

由于伺服电机响应频率远大于系统频宽，其数学模型可用一个惯性环节表示：

(1)

u为控制量；Kt为扭矩常数；te为电气常数；τm为输出扭矩。

根据牛顿第二定律，滚珠丝杠的动力学方程为：

(2)

i为减速器传动比；Jeq为折算至丝杆的总惯量；Beq为等效黏性阻尼系数；R=l/2π为丝杆转角到平动的转换比；θm为电机转角；η为丝杆的机械效率；p为承压筒内油压；A1为活塞推杆作用面积。其中，等效转动惯量Jeq可表示为：

(3)

Jm为伺服电机转子惯量；Js为滚珠丝杆惯量；mp为活塞推杆的质量；l为丝杆导程。

1.2 加载液压缸模型

加载液压缸的主要结构如图3所示。本文以一个刚度已知的碟簧组作为加载对象，分析加载装置的力跟踪性能。加载缸活塞与被加载物之间安装了一个传力装置，用以承受其他类型的被加载对象可能产生的转动和挠度。其他类型的加载对象将在以后的工作中加以研究，此处不再讨论。

图3 加载液压缸示意

加载液压缸的动力学方程为：

(4)

ml为液压缸活塞和传力装置的总质量；Bl为液压缸活塞和传力装置的粘滞阻尼系数；Fl为作用于加载对象上的实际力；kl为被加载物刚度。

1.3 承压筒压力模型

装置所采用的承压筒如图4所示。

图4 承压筒示意

承压筒内部的压力变化可以表示成以下形式：

(5)

βe为油液的有效体积弹性模量；V0为油液初始体积；ΔV为油液体积改变量；A2为加载液压缸的活塞面积；d1为电动缸的活塞推杆位移；d2为加载液压缸的活塞位移；L为活塞推杆的行程。实际上，油液的体积弹性模量会因混入空气而呈现非线性特性[6]。为了简化分析过程，可将式(5)右边的非线性环节替换为一个有界的时变系数，即

(6)

βl和βu分别为时变系数βv的上界和下界。当工作压力p∈[0 10] MPa时，根据文献[6]给出的计算方法可求得βe∈[240.4 1 605.3] MPa，对应的ΔV∈[0 9.2×10-5] m3，混入空气量按0.05%计算。由此可使原本的非线性模型转化为一个线性时变模型。

图5 新型电液力加载系统的控制框图

2 控制器设计

2.1 控制目标

力加载系统要求装置的输出力能够跟踪如下曲线：

Fl=Fc+Fdsin(2πfdt)

(7)

Fc为静态加载力，最大值为14 700 N；Fd为动态加载力，最大值为980 N；fd为动态力振荡频率，最大值为6 Hz。

对于控制设计来说，目标是保证系统频宽在6 Hz以上，力跟踪误差在±100 N以内。

2.2 双环复合控制器

对于长时间的加载工况，油液压力的测量相比动态力的测量更为便捷和可靠，因此采用压力反馈代替力反馈构造了半闭环的力控制结构，并基于双环复合控制的思想设计了压力控制环的反馈和前馈控制器，系统框图如图5所示。反馈控制包含了伺服电机速度控制器Gv(s)和加载缸压力控制器Gp(s)，其传递函数分别为：

(8)

伺服电机速度环采用PI控制，Kv和Ki=Beq/Jeq分别为速度环的比例和积分增益，主要用于电动缸驱动系统的零极点对消，提高其动态响应性能并消除转速跟踪静差。加载缸压力控制环则采用P控制，比例系数为Kp，用于提高系统的开环增益。

同时，为了进一步提高力跟踪精度，引入二阶微分前馈对压力环响应的相位滞后进行补偿：

Fp(s)=Kfvs+Kfas2

(9)

Kfv和Kfa分别为压力信号一阶和二阶微分的增益。联立式(1)～式(6)以及式(8)～式(9)，可以得到系统的开环传函Go(s)和闭环传函Gc(s)：

(10)

本节中仅给出控制器的形式，控制参数的最优取值将在下文的集成设计中得到。半闭环控制结构的可行性将在实验中进一步验证。

3 加载装置的性能指标

为了量化加载装置的性能指标，本节建立了一系列性能函数。借鉴定量反馈理论的思想[7]，根据时变参数取值的不同，将原模型表示为一族线性时不变模型的集合，对集合内的每一个模型进行分析，选择最差的计算结果作为性能指标的度量值，这样可保证参数变化时系统性能仍能够满足设计要求。

3.1 稳定性和频宽

电液力加载装置的闭环稳定性采用幅值裕度和相位裕度表示：

(11)

ωB=minω||Gc(jω)|=

(12)

3.2 力跟踪误差

加载装置最主要的功能在于输出特定的载荷谱。在误差评定中，只考虑输出力的幅值误差。加载力的幅值为：

Fl=|Gc(jωd)|Fr,ωd=2πfd

(13)

由此得到力跟踪的最大幅值误差为：

EF=max|Fr(1-|Gc(jωd)|)||βv∈[βlβu]

(14)

3.3 伺服电机的功率需求

伺服电机的功率需求是电动缸选型中的重要指标。电机功率过小时，系统将无法产生足够的压力；而电机功率过大时，其本身的转子惯量也会随之增大，不利于快速响应，同时造成了成本的浪费。已知加载力时，可以得到加载缸活塞的运动为：

(15)

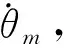
(16)

除了电机功率，还必须考虑电机运行中的最大所需转矩Tmax和转速nmax：

(17)

同理，滚珠丝杆运行中所需的最大线速度vmax和最大推力Fmax可表示为：

(18)

式(17)～式(18)给出的指标不作为具体的设计目标，但仍需在电动缸选型时加以验证，以避免出现控制量饱和的情况。

4 加载装置的集成设计

4.1 设计目标

为了从系统性能和装置成本2个方面获得最优设计，本文要达到的目标有2点：最小化力跟踪误差和最小化伺服电机功率。待设计的参数为：传动比、滚珠丝杆导程、电动缸活塞外径与长度、电机速度增益、加载缸压力环增益、前馈比例和微分增益。而加载液压缸和传力装置的相关参数由装置的最大加载力决定，不在集成设计的范围内。根据线性权重法，集成设计的目标函数可以表示为：

(19)

f(X)为目标函数；α1和α2为权重系数；X为包含设计参数的向量；WN和EN分别为归一化的电机最大功率和力跟踪误差。归一化的目的是避免各指标数量级的不同对数值计算产生影响，其中所用到的初值W0和E0来源于一个初步设计方案，其机械和控制参数是各自独立进行设计的。

4.2 最优问题的构造和求解

设计中除了要使系统的设计目标达到最优，还要考虑其他性能指标是否合理。同时，设计变量本身都被限制在一个有限区间内以减小计算量和确保收敛性。此外，由于在持续加载过程中无法对承压筒进行补油，其初始容积也应作为设计的约束条件以应对液压油的泄漏。因此，加载装置的集成设计可以归结为一个多目标约束优化问题：

(20)

其中，g1(X)=Glim-Gm,g2(X)=Plim-Pm,

g3(X)=ωlim-ωB,g4(X)=vmax-vlim,

g5(X)=Fmax-Flim,g6(X)=nmax-nlim,

g7(X)=Tmax-Tlim,g8(X)=VL-V0

Xi为第i个设计变量,Xil和Xiu分别为其上界和下界；Glim，Plim和ωlim分别为最小幅值裕度、相位裕度和频宽；vlim和Flim分别为丝杆的最大线速度和推力；nlim和Tlim分别为电机的最大转速和扭矩；VL为8 h内液压缸的最大允许泄漏量。约束条件的取值如表1所示。

表1 约束条件的取值

本文采用基于序列无约束最小化技术的粒子群算法[8]对优化设计问题进行求解。与其他优化方法相比，粒子群算法的全局搜索能力相对较强，适合于复杂非线性优化问题。按照表2给出的加载装置已知参数，优化算法的求解结果如表3和表4所示。

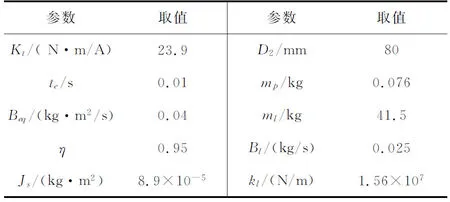
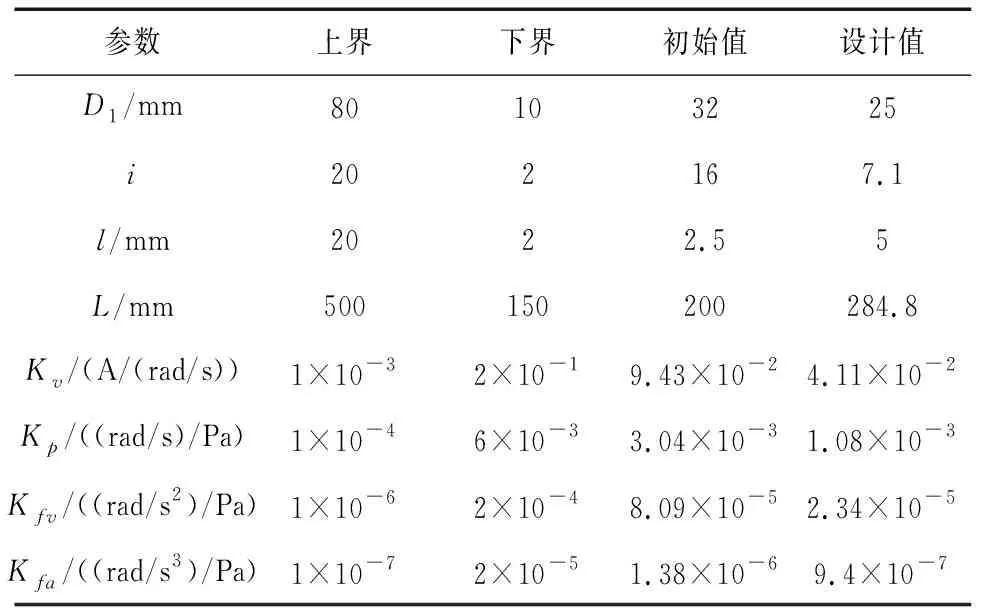
表3 优化设计结果(设计参数)

表4 优化设计结果(设计目标)

从优化结果中可见，相比于机械和控制各自独立进行设计的方案，集成设计方案使系统所需的伺服电机功率大大减小，同时也进一步提升了加载装置的力跟踪精度。

5 实验验证

5.1 实验平台搭建

新型电液力加载实验平台主要由液压执行机构(如图6所示)、驱动系统(如图7所示)和工业控制计算机等3部分组成。

图6 液压执行机构

图7 驱动系统

根据设计结果，选用上海冀望SEA802型直线式伺服电动缸，配备7∶1减速器，滚珠丝杆导程为5 mm，其活塞推杆的最大轴向载荷9 kN，最大线速度为0.375 m/s。选择高创PH06MB230(400 W)型伺服电机驱动电动缸，其额定转矩和额定转速分别为1.273 N·m和3 000 r/min，均符合设计要求。伺服驱动器以及所有传感器通过EtherCAT总线，与1台BECKHOFF公司C6640型工业控制计算机进行通信，采样频率设为200 Hz。

5.2 动态力加载实验结果

以静态幅值14 700 N、动态幅值980 N、频率6 Hz的指令力作为输入信号，加载装置的力跟踪实验结果如图8～图11所示。实验中的前10 s为预加压阶段，此阶段的实验曲线没有在图中显示。

从图8和图10可见，该载装置能够良好地跟踪6 Hz动态力轨迹，且最大跟踪误差不超过100 N，约占加载力幅值的0.64%，满足了设计要求。

图8 动态力跟踪曲线

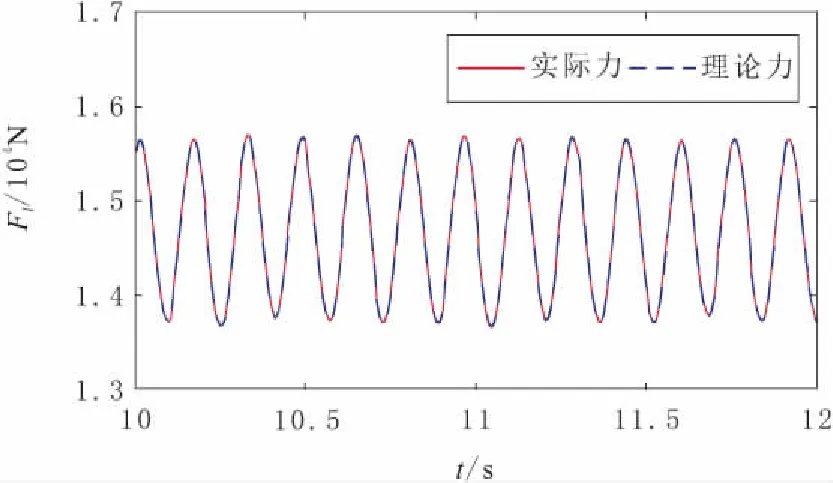
图9 实际力与理论力的对比

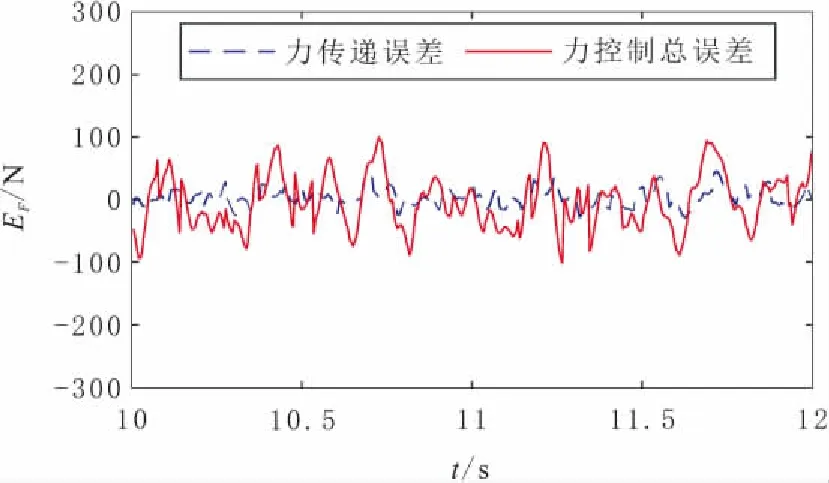
图10 力跟踪的总体误差与传递误差

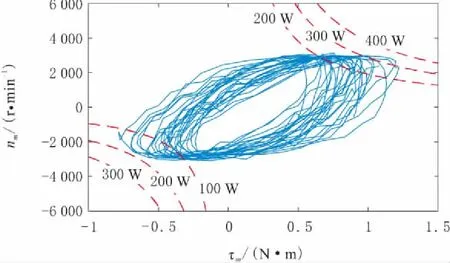
图11 伺服电机的功率曲线

图9为加载对象的理论输出力和实际作用力的对比。其中，理论输出力指的是加载缸活塞上的作用力，由油压乘以活塞面积得到。理论上，由于本装置采用半闭环控制结构，其理论输出力与加载对象的实际作用力之间会存在一定的传递误差。而从图9～图10中可以看出，理论输出力与实际作用力基本保持一致，两者之间的传递误差相较于总体误差而言要小得多，进而验证了半闭环力控制结构的可行性。

由图11可知，伺服电机的最大转矩和转速的大约为1.2 N·m和3 000 r/min，都分别接近该型电机的额定转矩和额定转速。伺服电机的运行中的最大功率约为350 W，未超过其额定功率。当输入指令力的频率或幅值进一步增大时，驱动系统在短时间内仍有大约90%的过载能力。

6 结束语

研究了一种新型电液力加载装置的集成设计方法。建立了完整的系统模型，构造了同时包含机械和控制参数的约束优化问题，采用粒子群算法进行了求解。根据设计结果搭建了实验平台，验证了半闭环力控制结构的可行性。同时，实验结果也表明集成设计方法能够有效地优化系统参数，在保证系统满足预定指标的同时充分利用电机的驱动能力，使得加载装置所需的电机功率大大减小，达到了优化成本的目的。