基于回归分析和灰度模型GM(1,1)的民勤县需水量预测
2018-09-28姜田亮石媛媛王雅云
姜田亮,石媛媛,王雅云
(甘肃农业大学水利水电工程学院,兰州 730070)
位于西北干旱内陆地区的民勤绿洲是阻挡巴丹格林沙漠和腾格里沙漠汇合的一条绿色廊道,也是保障武威盆地和河西走廊不受风沙侵入的天然生态屏障,是治沙的“桥头堡”。一旦这道屏障失守,整个河西走廊将会被沙漠拦腰折断,甘肃乃至内地的大部分地区都将面临沙漠的直接威胁[1]。自2004年6月红崖山水库断流,由于地表水总量受限,过度超采导致地下水迅速下降,使得依靠地下水存活的天然植被开始退化死亡,如此恶行循环,直接破坏了水资源和生态环境的平衡状态[2]。民勤地区水资源供需矛盾日益突出,面临着严峻的水资源短缺问题。水资源是农业之命脉、工业之血脉,是恢复生态环境的重要因素,是人类赖以生存的物质基础,对国民经济的发展有着举足轻重的作用[3]。要想有效解决该地区水资源短缺的问题,须从供需关系上着手,对水资源进行全面的评价,即进行准确的需水预测[4]。针对民勤县面临的水资源问题,本文基于民勤县近8 a的经济发展及水资源统计数据,采用灰色模型GM(1,1)及二元回归分析方法,对民勤县农业用水、工业用水、生态用水、城乡生活用水及禽畜用水量分别进行预测,以期为民勤县合理的水量配置提供决策参考。
1 数据来源及分析方法
本文所采用的水量数据包括农业灌溉用水、工业用水、生态用水、城乡生活用水、城市用水、畜禽用水及总用水量,社会经济数据主要为地区生产总值(GDP)。数据时间跨度为2008—2015年,各数据来源于《民勤县国民经济和水发展统计资料汇编》[5]。
首先利用2008—2014年的水量与社会经济数据进行相关性分析,以地区生产总值为自变量,分别以各用水量为应变量进行回归计算,分析其相关性。对相关性较好的结果进行组合,得出相应的线性模型后,对2015年各分项用水量进行预测,进而得出总用水量。其次基于相关成果,利用灰度模型GM(1,1),使用Matlab进行编程,利用2008—2014年的水量数据对2015年分项用水量进行预测。最后,将上述2种方法所得预测值与2015年实测数据进行对比分析,校验方法的合理性。具体技术路线如图1所示。

图1 技术路线图
2 需水量预测
目前有关县级地区的需水量预测研究比较少,最常用的需水量预测方法包括用水定额法、时间序列法、灰色系统法、生长曲线法、生产函数法、回归分析法和系统动力学法等[6]。但上述方法在应用中有各自的局限性,用水定额法[7]只能用于各类需水量的定额数据(如生态需水量)比较完备的地区;时间序列法仅适用于用水趋势具有较好规律性的地区[6];灰色系统法在需水序列零增长、负增长或数据不平稳时,预测效果不理想[8];生长曲线法[5]要求所预测的对象符合某种生长规律;生产函数法将科布道格拉斯函数应用于工业需水量预测,通常不适用于其他类别需水量的预测[6];许多学者对回归分析法的预测期限存在不同的意见,在实践中用回归模型进行长期预测和短期预测的研究均较少[9];系统动力学法预测模型过于复杂,若对各类用水规律认识不充分,则该方法会产生较大误差[7]。鉴于上述模型各有缺陷,本文分别使用回归分析法和灰色模型GM(1,1)对民勤县需水量进行预测并作对比分析,以期得到较为准确的预测结果。
2.1 回归分析法
回归分析法用于研究一个应变量对应一个或多个自变量的相关分析,通过建立单一变量或多变量之间的线性或非线性数学模型,探索变量之间的关联变动的规律[10]。
具体方法是:建立应变量yi与p个自变量xi1、xi2、…、xip的模型。
yi=a1xi1+a2xi2+…+apxip+ε
(1)
式中:xi1、xi2、…、xip为影响地区生产总值y的分项用水量;ε为修正系数。
民勤县2008—2014年各项用水量及地区生产总值如图2~3所示。由图4可见,农业用水占比最大,约84%,生态用水其次,约11%,城乡生活用水及畜禽用水量各占2%,而工业用水量占比最少,不足1%。总用水量总体呈下降趋势,7 a间下降了约15%,其中农业用水下降最快,7 a间下降约52%,生态用水有了显著的增加,7 a增加80%。工业用水量则小幅度上涨,城乡生活用水量及畜禽用水量无明显变化。民勤地区生产总值年均增幅为8.3%。
2.1.1 单因子回归
农业用水、生态用水和地区生产总值之间的相关性分析如图5、6所示及表1所列。其中农业用水量与地区生产总值之间的相关系数为0.796<0.874,相关性较低,不能直接进行回归分析,而生态用水量与地区生产总的相关系数为0.925>0.874,P<0.01,即在0.01的水平上线性关系合理且显著,据此建立回归模型。
y=13.86+0.0047x
(2)
式中:x为生态用水量;y为地区生产总值。
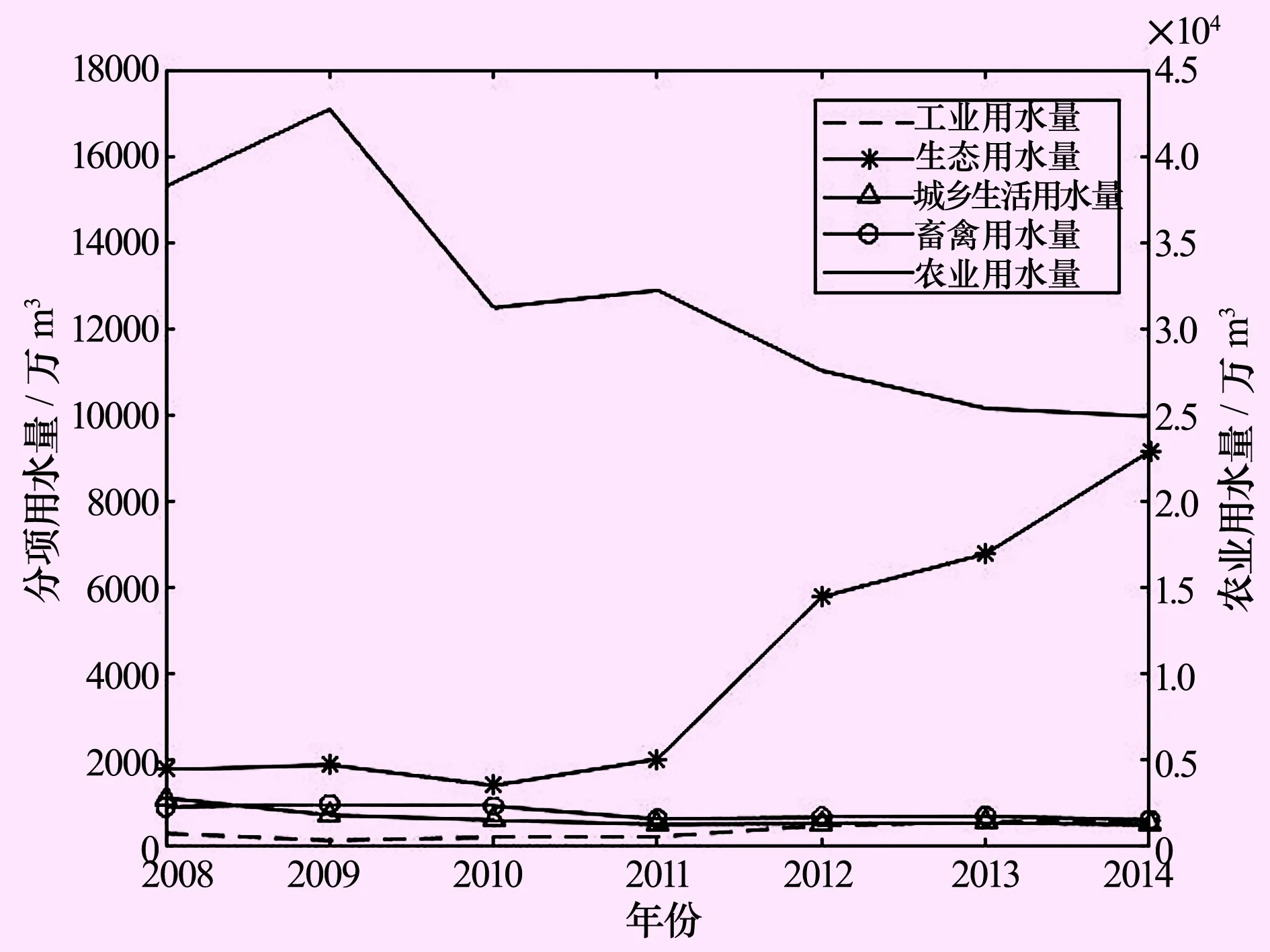
图2 各用水量变化趋势图

图3 总用水量及地区生产总量趋势图

项目相关系数RR0.01P农业用水量和地区生产总值0.7960.8740.0069生态用水量和地区生产总值0.9250.8740.0005
由此可见,近年来民勤县节水灌溉取得了明显的成效,水资源利用效率得到显著提升,农业用水量逐年减少,而地区生产总值却稳定上升。另外生态用水量的提高与地区生产总值的提高有显著的相关性,“绿水青山就是金山银山”,说明重视生态恢复有益于生产总值的提高。
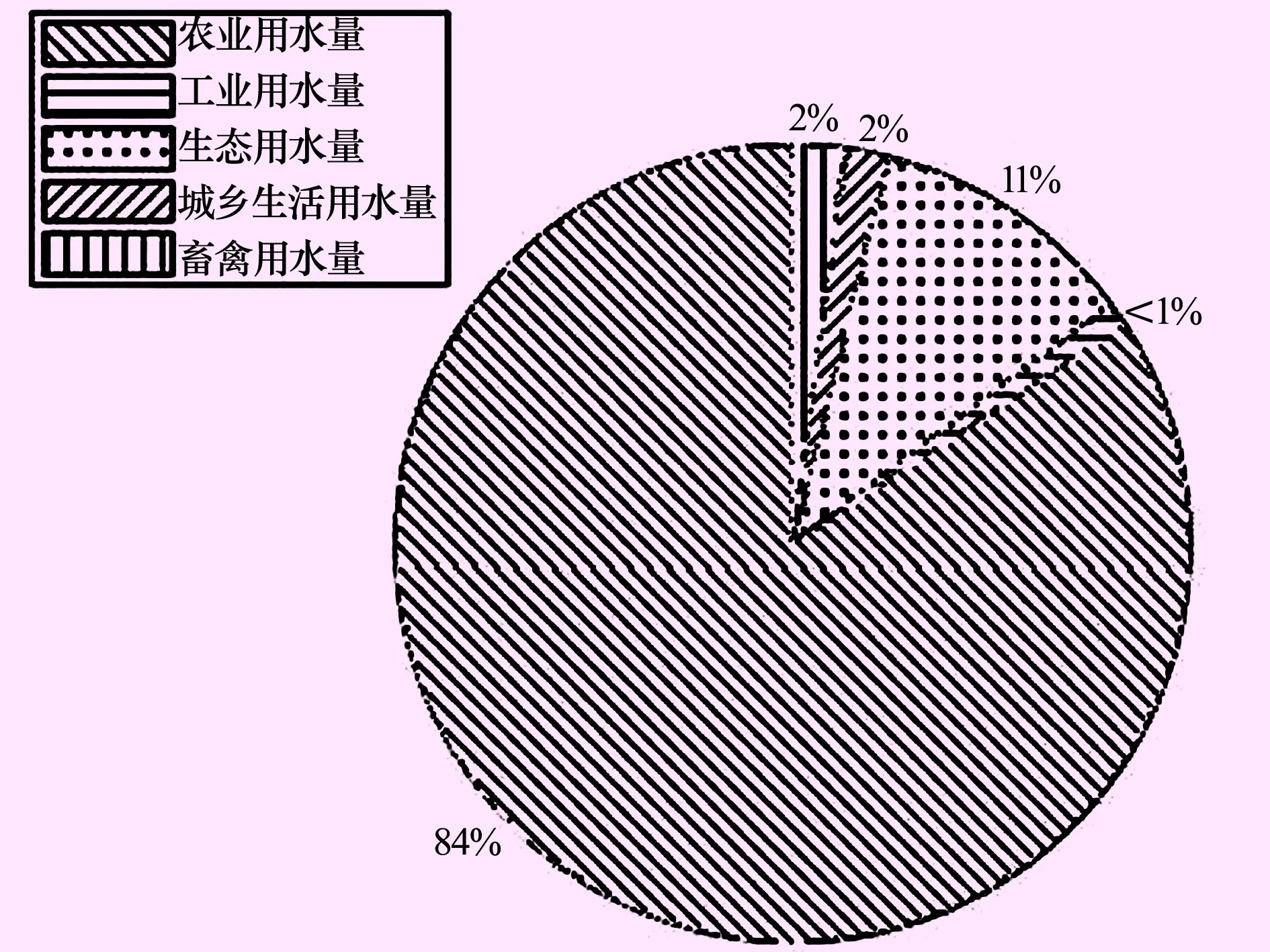
图4 分项用水量所占比图
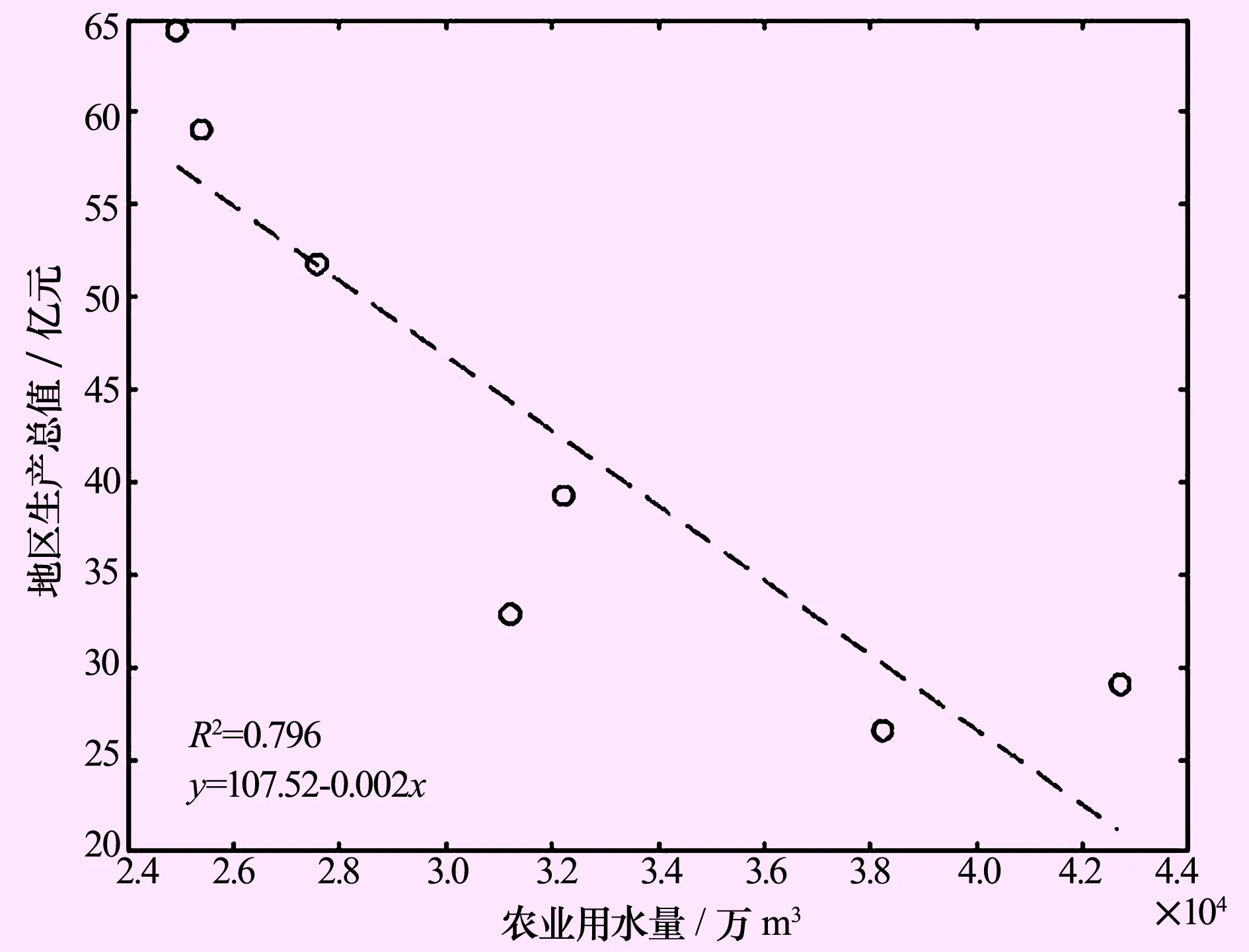
图5 农业用水与地区生产总值关系图
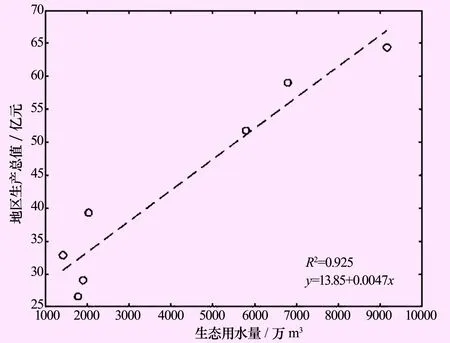
图6 生态用水与地区生产总值关系图
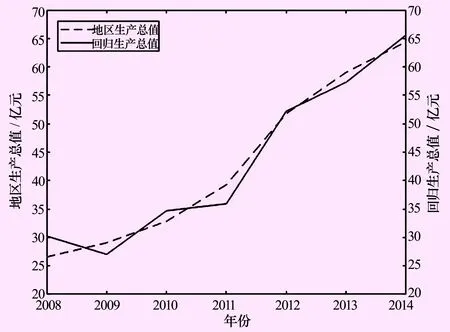
图7 二元回归分析结果图
2.1.2 二元回归模型
将农业用水量、生态用水量作为应变量,地区生产总值作为因变量,进行二元回归分析。
y=55.138+0.0033x1-0.0008x2
(3)
式中:x1为生态用水;x2为农业用水;y为地区生产总值。
分析结果如表2所列及图7所示。相关系数0.973 1大于检验系数0.874,P值小于0.01,即在0.01的水平上应变量和自变量相关程度高及显著性明显。

表2 二元回归相关性分析及差异分析表
2.1.3 三元回归模型
以地区生产总值为因变量y,以工业用水、城乡生活用水、畜禽用水3项指标作为自变量x,进行回归分析,回归系数如表3所列。
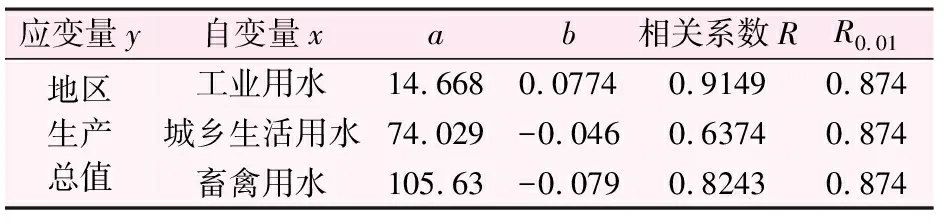
表3 分项水量相关分析表
注:y=a+bx。
由此可见,工业用水与地区生产总值的相关性较为明显,相关系数为0.914 9>0.874,即在0.01的水平上显著相关;城乡生活用水及畜禽用水的相关系数分别为0.637 4、0.824 3,均小于检验系数0.874,与地区生产总值的相关度较低,不能准确进行分项水量的预测,因而在此基础上进行三元回归分析。
y=40.52-0.004x1-0.0263x2+0.0632x3
(4)
式中:x1为畜禽用水;x2为城乡用水;x3为工业用水。分析结果如图8所示及表4所列,相关系数大于检验系数,P值小于0.01,即在0.01的水平上应变量和自变量相关程度高及显著性明显。

表4 三元回归相关性分析及差异分析表
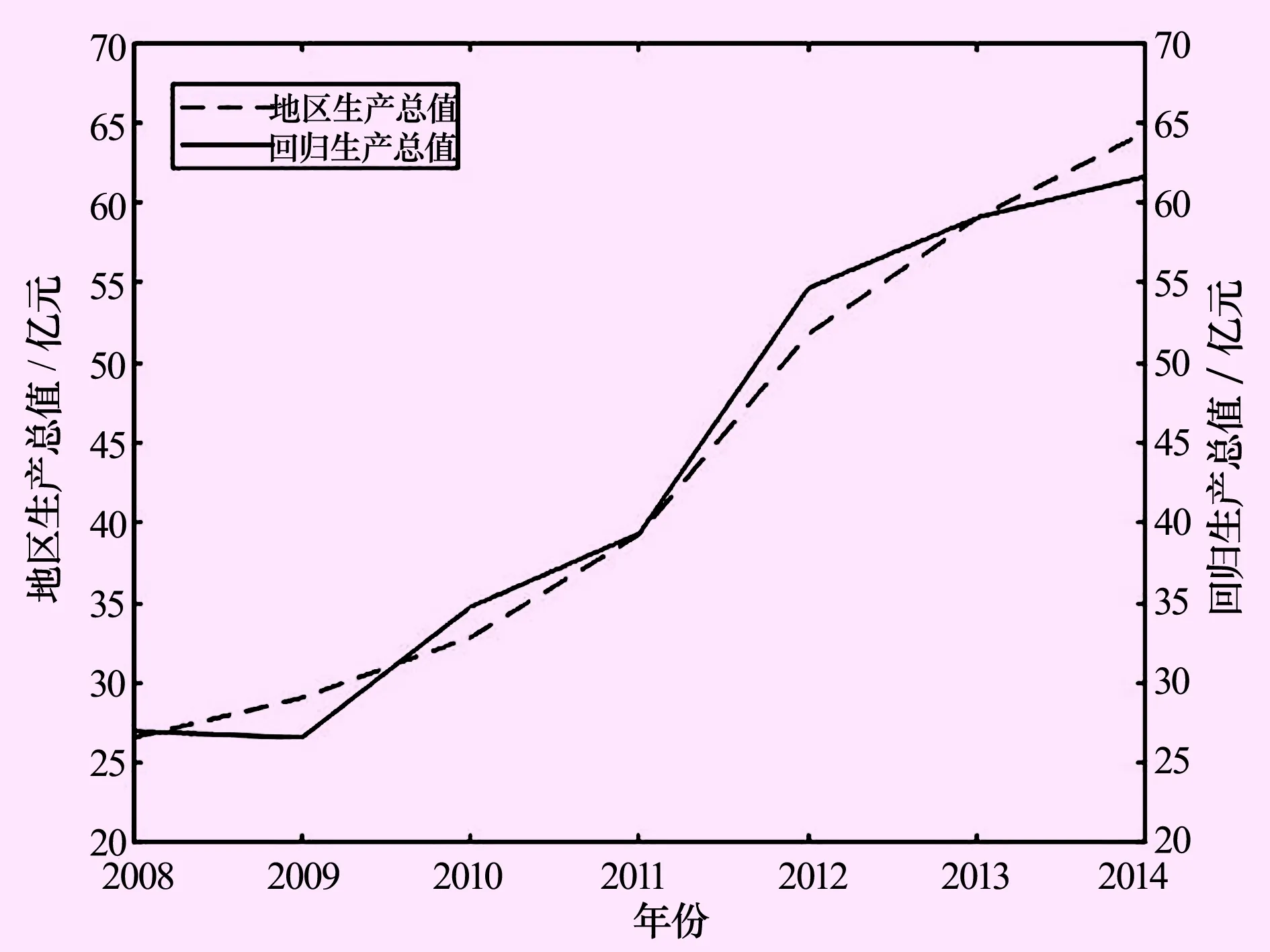
图8 三元回归分析结果图
2.1.4 回归分析预测需水量
利用上述回归模型成果,对2015年总用水量进行回归预测。2015年民勤县地区生产总值为69.56亿元,由式(2)计算可得,生态用水量为11 851.06万m3,将该值代入式(3)可得,农业用水量为22 081.65万m3。同样可得到,2015年工业用水量为709.2万m3。
通过计算发现,畜禽用水量约为农业用水量的0.025,因此2015年畜禽用水量预测为552.04万m3,代入式(4)可得,城乡用水量的预测值为520.53万m3。总用水量为35 714.48万m3。
2.2 灰色模型GM(1,1)预测法
常规GM(1,1)模型是灰色模型的基础,是包含一个单变量的一阶微分方程构成的模型[11-12]。
2.2.1 灰色模型原理
(1) 已有用水量序列数据为x(0)(k)={x(0)(1),x(0)(2),…,x(0)(n) },对该数据作累加处理得到x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n) },k=1,2,…,n。
因此,诸如示例1,若采用方案三,信号路由的复杂程度与方案一相同。差别在于,所有的控制过程均发生在DCS中。
(2) 建立GM(1,1)模型微分方程。即:
(5)
式中:α为发展灰数;μ为内生控制灰数。
(3) 构建矩阵B和向量Y,即:
(6)
Y=[x(0)(2)+x(0)(3),…,x(0)(n)]T
(7)
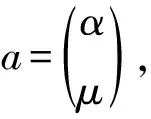
a=(BTB)-1BTY
(8)
(5) 求解微分方程可得预测模型:
K=0,1,2,…,n
(9)
(6) 累减还原得到原始数列的灰色预测模型:
(10)
(7) 灰色模型的精度检验一般有3种方法:相对误差检验法、关联度检验法和后验差检验法,本文使用后验差检验法。计算残差得:
(11)
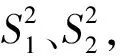
(12)
(13)
后验差比为:
(14)

表5 精度检验等级参照表
2.2.2 灰色模型预测需水量
利用民勤县2007—2014年的数据进行模型率定,根据式(8)和表(5)计算得出α、μ,将其代入式(9)可分别得到农业用水、工业用水、城乡生活用水及畜禽用水累计预测公式,得到5个单一灰色GM(1,1)模型并用后验差法进行检验。本文利用Matlab进行编程,代入数据后运行,结果如表6所列。

表6 GM(1,1)模型后验差率定结果表
由表6可以看出,各模型的精度等级均为合格以上,满足精度要求,由此可见所建模型合理、可行。
根据建立的各模型公式对民勤县2015年的各用水量进行预测,得到农业用水量为21 661.47万m3,工业用水为783.6万m3,生态用水为12 242万m3,城乡生活用水为447万m3,畜禽用水量为533万m3,总用水量为35 667.07万m3。
2.3 小 结
综上采取不同方法取得的2015年民勤县需水预测成果如表7 所列。

表7 2015年民勤县需水预测表 /万m3
由表7可知,2015年民勤县实际用水总量为35 853万m3,而回归分析预测结果与灰度模型预测结果分别为35 714.48万m3和35 667.07万m3,相对误差分别为0.3%和0.5%,即回归分析预测结果与实际结果最为接近。对实际分项用水量与回归分析预测结果进行差异性检验,得到p值为0.996 5。对灰度模型预测结果与实际分项用水量进行差异性检验,得到p值为0.995 3。因此,用回归分析法对民勤县的用水量预测分析,可以得到更为准确的结果,且逻辑清晰、计算简单,可为类似干旱半干旱地区的需水量预测提供参考。
基于上述2种模型结果对2018年进行预测,得到结果如表8所列。
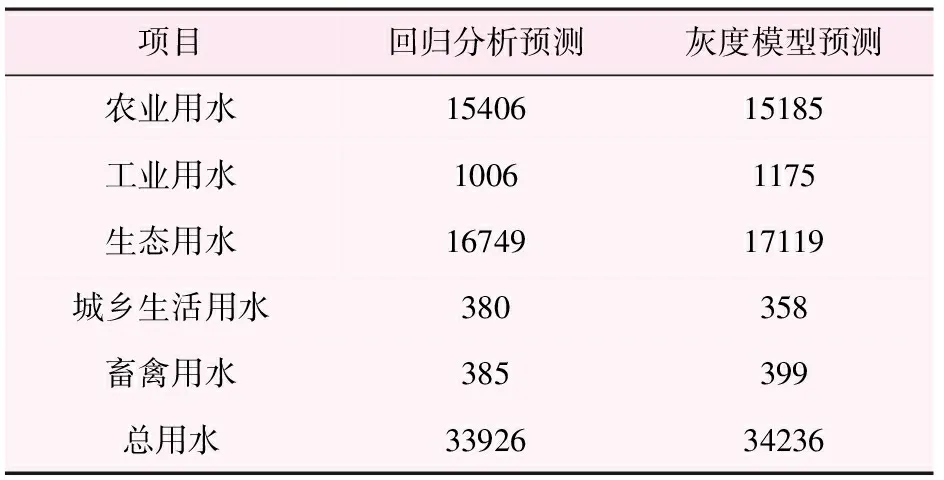
表8 2018年民勤县需水预测表 /万m3
由表8可知,利用回归分析模型和灰度模型分别预测出:2018年民勤县需水量分别为33 926万m3和34 236万m3。对2种模型所得分项用水量进行差异性分析,得到p值为0.991 1,即模型预测结果差异性小,可为民勤县水资源优化配置提供参考。
3 结 语
(1) 对民勤县近7 a的用水量结构及特征进行分析,结果表明:农业用水占比最大,约为84%;生态用水占比约为11%;城乡生活用水和畜禽用水各占2%;工业用水占比不足1%。总用水量总体呈下降趋势,7 a间下降了约15%,其中农业用水下降最快,7 a间下降约52%,生态用水有了显著的增加,7 a增加80%。工业用水量则小幅度上涨,城乡生活用水量及畜禽用水量无明显变化。
(2) 相关分析表明,近7 a,农业用水与地区生产总值呈负相关,而生态用水和工业用水与地区生产总值呈正相关,且相关度较高。二元回归分析表明地区生产总值与农业用水量及生态用水量有良好的相关性。工业用水、城乡生活用水及畜禽用水与地区生产总值可建立三元线性模型,且有良好的相关性。
(3) 基于近7 a社会经济和用水量数据,采用回归分析法和灰度模型法对2015年民勤县用水量进行预测,可得到精度良好的预测结果,总需水量相对误差均在1%以内,分项水量预测值与实际值经差异性检验,p值均大于0.99。与灰度模型相比,回归分析法计算简单,且精度高、逻辑清晰,可供类似干旱半干旱地区水资源需水预测的研究参考。
(4) 从预测结果中可以看出,民勤县的农业用水将继续减小,工业用水对地区GDP的影响趋于增强,生态用水的增多将有助于民勤绿洲植被的恢复和生态的改善。民勤县的用水结构在未来几年内将朝着更为合理健康的方向发展,同时说明近些年来民勤县生态环境的治理取得了一定的成效。
(5) 在追求民勤地区GDP增长的同时,要注重水资源的分配和利用效率。在以农业为主的民勤县,传统的灌溉模式,即“浇地”不“浇作物”,使水资源浪费严重[7]。只有从根本上变革这一农业灌溉制度,减轻无效蒸发耗水,让有限的水分最充分地用于作物生长需要,才能在保证生产总值增长的同时为生态用水节省出更多的水资源。
