基于灰色关联分析的女大学生800 m跑成绩影响因素分析与模型构建

刘 昊

(中南财经政法大学 体育部，湖北 武汉 430064)

常规跑步运动成绩影响分析模型主要使用大数据样本以及统计学理论对运动成绩进行影响分析，模型多为专业运动员提供成绩分析服务，以便减少影响运动比赛成绩的因素.传统模型对女大学生800 m跑步成绩进行分析时，由于数据样本低，统计分析不全面，造成影响因素分析准确率较低以及响应时间较长的不足[1].针对上述问题，提出基于灰色关联分析的女大学生800 m跑成绩影响因素分析与模型构建.为了保证设计分析模型和分析过程的有效性，设定女大学生800 m跑步实验环境，使用两种不同成绩影响分析模型，对800 m跑步成绩影响因素进行分析，实验结果表明，提出的影响分析模型以及分析过程具备极高的有效性.

1 构建基于灰色关联的成绩影响分析模型

基于灰色关联成绩影响分析模型的构建先确立参考数列以及分析数列，由于分析数列与参数数列的量化式不同，因此进行数列无量纲化处理[2]，计算灰关联算子以及分析关联算子，完成基于灰色关联的成绩影响分析模型构建.

1.1 参考数列与分析数列的确立

与男性运动员相比，影响女大学生800 m跑步成绩的因素较多，并且影响因素较为复杂.构建成绩影响数列，将多种影响因素合并到影响数列中，与标准参考数列进行对比计算，此时成绩影响数列即作为对比数列，又作为参考数列进行对比分析[3].

其中身体机能因素还包括：克托莱指数、马氏躯干腿长指数、维尔维克指数、劳雷尔指数以及BMI指数.克托莱指数是表明身高肥胖程度的指标[4]，计算过程是：体重与身高的比值再乘以1 000，当克托莱指数大于400或小于330时，对女大学生中长跑、短跑等运动成绩具有较大的影响.马氏躯干腿长指数是表明身比例的重要数据，计算过程为：身高与坐高的差除以坐高再乘以100，马氏躯干腿长指数测量时，保证女大学生水平坐稳，小腿与大腿成90°，站立时躯干成180°自然收缩，但请勿后腰贴靠在墙上[5].马氏躯干腿长指数低于80对女大学生中长跑影响较大，其他因素不变的情况下马氏躯干腿长指数越高，中长跑比赛成绩越高，但马氏躯干腿长指数的提高会带来其他抑制因素的影响，比如身体运动协调性、技巧因素不易掌握等.维尔维克指数的计算过程为：体重乘以胸围和身高的比值，维尔维克指数反应的是运动员的身体长度、宽度、维度、厚度和密度，当维尔维克指数低于80或高于120时，对女大学生800 m跑步成绩有一定的影响.劳雷尔指数能够反映运动型肌肉、机体骨骼、内脏器官以及软组织的发育状况，是人体充实程度和营养状况的指数.计算过程为：体重与身高的三次幂之比乘以107，其中小于106.1或大于154.4时，会对女大学生运动成绩造成直接影响.

设女大学生身体机能因素数列为A1，其中克托莱指数为A11、马氏躯干腿长指数A12、维尔维克指数A13、劳雷尔指数A14、BMI指数A15,那么身体机能对比数列为A1={A11，A12，A13，A14，A15}.

状态因素与身体机能因素不同的是，身体机能在短时间内为定值，而女大学生身体状态会受情绪、健康状态以及生理状态所影响[6].设女大学生状态因素数列为A2，其中情绪影响为A21、身体健康状态影响为A22，以及生理状态为A23，那么身体状态对比数列为A2={A21，A22，A23}.

环境因素以及突发事件因素的影响都是客观影响因子，环境因素的影响主要包括：气候因素、跑步场地因素以及其他环境条件.突发事件因素的影响为随机影响，包括各种非抗拒性事件，但产生突发事件的概率较低.设比赛环境以及突发事件数列为A3，其中室外天气的影响为A31、受跑步场地影响为A32、其他跑步条件的影响为A33、突发事件的影响为A34，那么比赛环境以及突发事件数列为A3={A31，A32，A33，A34}.

技巧因素是影响女大学生800 m跑步成绩的主要因素，其主要包括跑步装备、跑步前热身状态、正确跑步姿势等，设运动技巧数列为A4，其中跑步装备为A41、跑步前热身运动为A42、正确跑步姿势为A43、其他为A44，那么比赛环境以及突发事件数列为A4={A41，A42，A43，A44}.则女大学生800 m跑成绩影响因素对比数列如公式1所示.

A={A1,A2,A3,A4}=

(1)

在标准分析情况下，设置参考数列B={B1，B2，B3，B4}，同时保证B1包含在数列{B11，B12，B13，B14，B15}中，B2包含在数列{B21，B22，B23}中，B3包含在数列{B31，B32，B33，B34}中，B4包含在数列{B41，B42，B43，B44}中.因为集合中包含大量指数、常数，因此采用不同算法进行对比.由于量纲不同无法进行直接对比计算，为此进行数列无量纲化处理.

1.2 数列无量纲化处理

根据上文确定的跑步成绩影响数列，对因克托莱指数、马氏躯干腿长指数、维尔维克指数进行计算，由于计算单位不同，因此无法直接进行对比计算，笔者采用无量纲化对数列进行处理[7].对比数列为A，设(xi，yi)∈A，其中i为变量，(xi，yi)代表影响集合的不同子集，对(xi，yi)的无量纲化处理方法有阈值法、指数法、标准化方法、比重法等等.因为阈值法计算简单，适用于不同数列的对比计，笔者采用阈值法对数列进行无量纲化处理.

对(xi，yi)内最佳数值进行确定，设(xi，yi)内最佳数值为f(x)，以最佳数值为中心提高或减低一个单位的成绩，即做f(x±a)，其中包含有n个单位，那么(xi，yi)的无量纲化处理等于(xi，yi)内的所有影响因素通过阈值法计算求和，求和次数为m，即做：

P(xi,yi)=Pn(x)+Pn+1(x)+...+Pn+m(x)

(2)

单个影响因素阈值法计算过程如下：

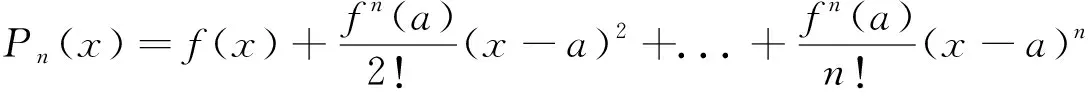
(3)

又因为在最佳数值f(x)，提高或减低一个单位的成绩为f(x±a)，换算f(x±a)的式如下：

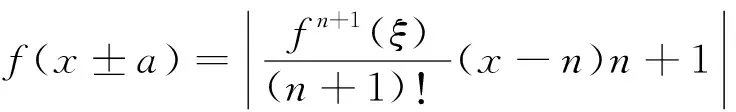
(4)

式中：ζ为灰关联系数.将公式(4)代入公式(3)，将整理后的公式代入公式(2)得到：

得出对比数列的无量纲化数据，通过灰关联算子的计算，将对比数列与参考数列进行对比分析.

1.3 灰关联算子的计算与处理

灰关联算子的计算结果会影响对比数列的计算结构和量值的大小.当灰关联算子取值较大时易造成对比数列计算结果产生正向偏离，如果灰关联算子取值较小，易造成参考数列结构向负向偏移，无论灰关联算子的取值增大还是减小均影响女大学生跑步成绩影响因素的分析.

灰关联算子的确定主要取决于数列计算宽容度、无量纲化阈值范围以及参考数列差.其灰关联算子计算如公式(5)所示.

Δ=±ζ(k)=

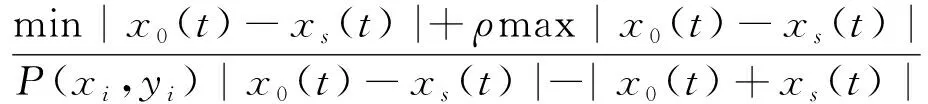
(5)

式中：x0为灰关联算子初始值，t为状态变量，ρ为分析条件系数，P(xi，yi)为数列无量纲化处理结果，同时根据数列无量纲化处理的量化式，对灰关联算子进行处理，其处理原则如下：

若P(xi，yi)|x0(t)-xs(t)|> |x0(t)+xs(t)|，那么△=ζ(k)，灰关联算子正影响因素分析.

若P(xi，yi)|x0(t)-xs(t)|< |x0(t)+xs(t)|，那么△=-ζ(k)，灰关联算子负影响因素分析.

通过参考数列与比较数列的确定以及数列无量纲化处理，完成女大学生800 m跑步成绩影响因素的确立，依托灰关联算子的计算，实现基于灰色关联成绩影响分析模型的构建.

2 成绩影响分析计算

成绩影响分析过程使用灰色关联成绩影响分析模型，对对比数列中影响因素无量纲化处理，判断出±ζ(k)，对比参考数列与对比数列，绘制出成绩影响曲线得出相应结论.

2.1 灰色关联分析计算

根据对比数列的无量纲化处理得出相关数列，代入灰关联算法中，与参考数列进行对比，女大学生800 m跑步成绩影响分析流程图如图1所示.

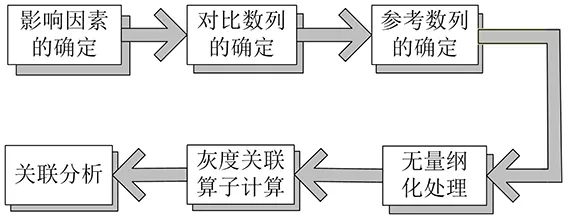
图1 灰色关联分析跑步成绩影响分析流程图

通过相关测试得出女大学生的相关身体机能条件，分析其身体状态，对其比赛环境进行研判，依托公式(4)进行灰关联算子的计算与处理得出ζ(k).根据灰关联算子ζ(k)，进行对比数列与参考数列的对比.其计算公式如公式(6)所示

(6)

式中x为女大学生800 m跑距离，a11为无量纲化处理的对比数列，V11为其参考数列，φ为根据灰关联算子ζ(k)调整结果，r为随机概率.

2.2 关联曲线的确定与影响因素分析

根据公式(6)对不同数列进行计算，得出女大学生800 m跑成绩影响曲线如图2所示.

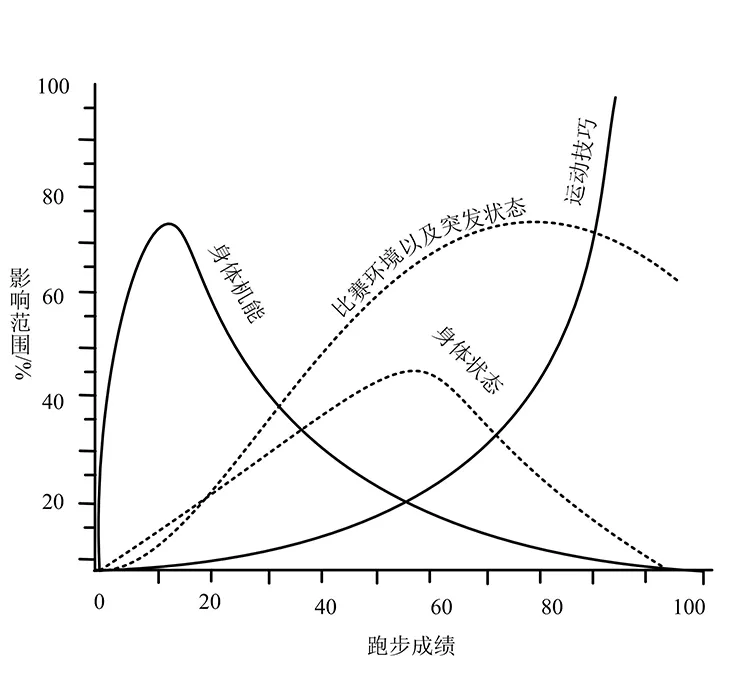
图2 女大学生800 m跑成绩影响曲线图

从图中得出女大学生800 m跑步成绩影响分析状态.当跑步成绩较低时，主要受身体机能因素影响，状态因素次之.随着跑步成绩的提高，身体机能因素影响逐渐降低，技巧因素影响逐渐升高.当跑步成绩及格偏下时，身体状态的影响高于身体机能的影响，同时比赛环境以及突发状态因素也非常重要.

3 实例分析

为了保证笔者构建的基于灰色关联分析的女大学生800 m跑成绩影响因素分析模型的有效性，进行仿真模拟实验.实验过程中，以不同的女大学生作为实验对象，进行跑步影响分析准确率模拟实验，对女大学生的不同运动状态以及身体机能进行模拟.

3.1 数据准备

为了保证仿真试验过程的准确性，对测试参数进行设置，笔者模拟实验采用不同的女大学生作为实验对象，利用两种不同的跑步运动成绩影响分析模型，进行测定分析准确率的模拟实验，并对模拟实验结果进行分析.由于不同方法中得到的分析结果与分析方式是不同的，因此，实验过程中需要保证实验环境参数的一致.实验参数设置结果如表1所示.

表1 实验参数设置

3.2 准确率实验结果与分析

实验过程中，确定模拟的女大学生运动成绩在不同影响因素与影响环境的比例，利用两种不同的跑步运动成绩影响分析方法，分析其准确率的变化.在模拟实验结果曲线图中，利用Analysis功能消除模拟实验室人员操作和模拟仿真计算机设备因素产生的不确定度.针对不同的女大学生、不同的跑步运动成绩影响分析方法，进行影响分析准确率的模拟试验.其试验结果对比曲线如图3所示.

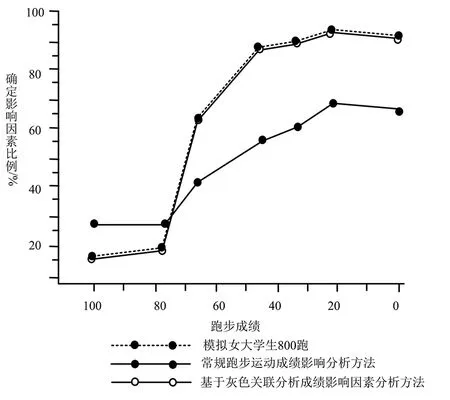
图3 试验结果对比曲线图

实验对比结果显示，笔者设计的基于灰色关联分析成绩影响因素分析方法比常规跑步运动成绩影响分析方法确定的因素比例精确高，与模拟量基本吻合，达到了设计要求.女大学生跑步成绩在80至100分之间时，模拟比例为15%～20%，基于灰色关联分析成绩影响因素分析方法(笔者设计方法)，通过灰色关联分析计算以及模型分析，确定影响因素模拟比例为15%至20%，与实验模拟量相差小于1%.在模拟女大学生跑步成绩为60至80分之间，本来设计方法与常规方法，确定影响分析因素较为准确.当女大学生跑步成绩低于60分时，模拟影响因素比例快速上升，笔者设计方法能够识别不同影响因素的变化，而常规方法能够分析出影响因素的变化趋势，但分析能力分析精度不够.采用第三方分析软件进行准确率分析，利用跑步成绩由0至100分区间的所有影响因素比例，得出笔者设计方法影响分析准确率为99.74%，常规设计方法影响分析准确率为47.29%，从而得出提出的影响分析方法比常规分析方法，在女大学生800 m跑步成绩分析影响准确率上高52.45%.

3.3 响应时间实验结果与分析

设置女大学生数量，根据相关体能测试获得相关女大学生的运动技能情况，模拟设置女大学生的运动状态，以及其他影响因素.利用两种跑步成绩影响因素分析方法，进行响应时间模拟实验.实验过程中同样采用Analysis第三方分析记录软件，对实验过程与结果进行记录与分析，并将结果显示在本次实验对比结果曲线图中.针对不同的女性大学生、不同的跑步运动成绩影响分析方法，进行分析响应时间模拟实验.其实验结果对比曲线如图4所示.

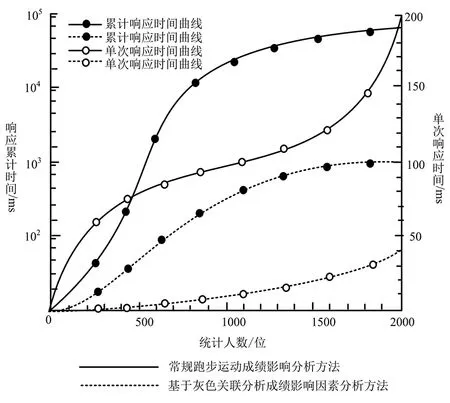
图4 试验结果对比曲线图

实验对比结果显示，笔者设计的基于灰色关联分析成绩影响因素分析方法累计响应时间与单次相应时间，均明显低于常规跑步运动成绩影响分析方法.在分析统计人数为500人时，常规跑步运动成绩影响分析方法，单次响应时间快速提升.当统计人数为100人时，单次性时间为25 ms；当统计人数为250人时，单次性时间为80 ms；当统计人数为500人时，单次性时间为92 ms.累计响应时间从0增至1 040 ms，累计响应时间与单次响应时间均成指数型上升.当统计人数超过500人低于1 000人时，常规跑步运动成绩影响分析方法，单次相应时间保持快速提升；当统计人数超过700人时，单次响应时间超过100 ms，同时累计响应时间超过10 000 ms.因分析样本较少分析算法计算不确定度较高，常规设计方法通过现有数据不断挖掘处理，造成响应时间过长.当统计人数超过1 000人低于1 500人时，单次响应时间由110 ms增加至125 ms,累计响应时间由10 000 ms增加至25 000 ms，即进行1 500人统计需要25 s.当统计人数超过1500人到达2 000人时，单次响应时间由110 ms突增至200 ms，继续呈指数型增长，累计响应时间达到90 000 ms，即累计90 s.

基于灰色关联分析成绩影响因素分析方法，整体上分析单次响应时间与累计响应时间均较低，响应时间较低带动对800 m跑成绩影响因素的快速分析，且保证良好的影响分析准确性.当统计人数低于500人时，单次响应时间保持高速运行，平均低于10 ms，累计响应时间不超过80 ms.当统计人数超过1 500人到达2 000人时，单次响应时间达到最高40 ms，累计响应时间达到1 000 ms，说明设计的基于灰色关联分析的女大学生800 m跑成绩影响因素分析模型能快速响应.

采用第三方分析软件进行响应时间统计，加权分析计算，得出常规设计方法影响分析平均响应时间为112 ms，笔者设计方法影响分析平均响应时间为25 ms，从而得出提出该方法比常规方法的分析响应时间少77.68%.

4 小结

笔者提出基于灰色关联分析的女大学生800 m跑成绩影响因素分析与模型构建，基于数列关系的确定以及无量纲化的处理，实现笔者的研究.实验数据表明，笔者设计的方法具备极高的有效性.希望笔者的研究能够为运动成绩影响因素分析提供理论依据.