用于电池储能系统的级联式电力电子变压器均衡及协调控制
2018-09-27孙玉巍李永刚刘教民李正文
孙玉巍, 付 超, 李永刚, 刘教民, 李正文
(1. 华北电力大学电气与电子工程学院, 河北省保定市 071003; 2. 国网辽宁省电力有限公司, 辽宁省沈阳市 110006)
0 引言
为应对风力、光伏等可再生能源发电对电网安全稳定运行带来的挑战,大容量电池储能系统(battery energy storage system,BESS)已成为国内外研究热点,对平抑新能源功率波动、调峰调频及提高电能质量具有重要的意义[1-3]。
大容量BESS通常由功率调节系统(PCS)接入中、高压等级电网,受制于功率器件的耐压水平,模块化级联PCS拓扑成为大容量BESS的发展方向[3-5]。近年来国内外广泛研究的级联式电力电子变压器(power electronic transformer,PET)在交流侧采用级联H桥(cascaded H-bridge,CHB),可实现交流低谐波,直流侧采用隔离双向DC/DC变换器(isolated bidirectional DC/DC converter, IBDC),可实现电压及功率的灵活控制和电气隔离,便于储能电池的分布式配置及降低安全隐患,非常适合大容量BESS场合[6-7]。下文将用于BESS的级联式PET简称为PET-BESS。
以往较多文献[8-10]对级联式PET控制策略进行了研究,在CHB级采用双闭环控制来控制网侧电流和直流链电压,在IBDC级采用移相调节控制输出电压及功率均衡,但均适用于IBDC并联输出场合。而在BESS应用中,IBDC输出端独立接分列的电池单元,除了网侧有功功率、无功功率、直流链电压的控制外,一个重要的问题是各电池单元的荷电状态(state of charge,SOC)需要进行均衡化处理[11],以保证系统额定容量及提高可靠性。
文献[6]提出采用CHB及IBDC拓扑的双向可拓展BESS,设计了其分布式控制策略;文献[12]针对基于CHB+IBDC的PET-BESS提出自抗扰控制策略,以提高双向功率翻转时系统的动态响应,但均没有对电池SOC均衡问题进行研究。文献[13]提出基于特征谐波消除脉宽调制法(SHE-PWM)的差异化充放电控制,可实现电池SOC均衡,但该低频相控的方法及各模块特定的触发角,将使系统总输出功率范围变窄,且网侧波形质量及动态调节能力也受限。文献[14-16]基于载波移相正弦脉宽调制(CPS-SPWM),通过注入零序电压调节各H桥单元参考电压及交流输出电压,不影响总功率即可实现SOC均衡,但由CPS-SPWM谐波消除机理所决定,各单元参考电压偏移将造成低次谐波消除不完全。且上述SOC均衡方法在总功率方向确定的情况下,子模块功率只可调节大小,不能调节方向,一定程度上限制了电池SOC的收敛速度。
文献[17]为降低CHB开关损耗及提高子模块功率差异较大时系统的稳定运行域,提出了一种混合脉宽调制(HPWM)多电平调制方法,在不影响总功率及谐波特性的条件下,子模块功率的大小及方向均可不同。根据这一特性,本文针对PET-BESS提出基于HPWM的电池均衡策略,以实现电池单元的双向差异化充放电。此外,为解决HPWM开关函数非线性时变以及功率指令扰动易造成直流链电压波动较大的问题,提出IBDC直流链电压协调控制策略,将CHB开关函数及功率指令的乘积作为前馈,以抑制直流链电压波动。最后,通过仿真及实验验证了所提方案的正确性和有效性。
1 PET-BESS系统分析
1.1 拓扑及动态模型
单相PET-BESS电路拓扑如图1所示,由输入级CHB整流电路、直流链电容Cdc以及后级IBDC电路及其所连接的电池单元构成。图中:vsa和ia分别表示电网电压和电网电流;Ls为交流滤波电感,Rs为其内阻。vhi和vdci分别为第i(i=1,2,…,N)个子模块的交流电压及直流链电压,vbi为第i个电池输出电压;idci和iLi为电容Cdc前后侧直流电流;nt为IBDC高频隔离变压器变比,Lt为其折合至一次侧的等效漏感;各模块参数相同。
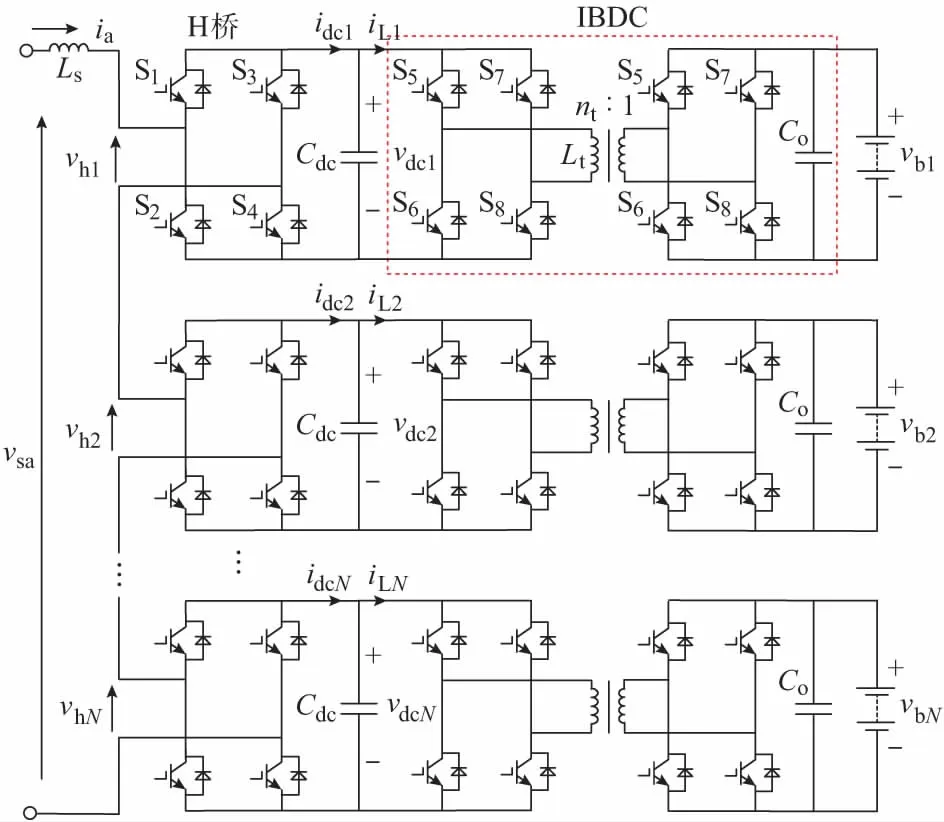
图1 级联式PET-BESS主电路拓扑Fig.1 Topology of main circuit of cascaded PET-BESS
本文CHB采用HPWM方法(在第2节阐述),虽然各模块开关函数分配及调制方式与传统SPWM方法不同,但其总调制波仍为正弦信号,总的交流输出电压为多电平正弦脉宽调制(PWM)波,因此对其建模时可同传统CPS-SPWM一样,忽略PWM波形中的高频分量,只考虑基波分量,从而获得占空比描述的动态平均值模型,如式(1)所示:
(1)
式中:da为总占空比调制信号,即总调制波。
为建立CHB系统dq坐标系数学模型,构造与图1中CHB系统正交的虚拟系统动态方程为:
(2)
式中:vsm为虚拟电网电压,可由实际电压vsa经单相锁相环(PLL)获得;im为虚拟电网电流,由虚拟系统输出;dm为虚拟调制波,由控制系统得到。

(3)
式中:ω为电网基波角频率;vd,id,dd和vq,iq,dq分别表示d轴和q轴的电网电压、电网电流及调制信号,若坐标变换时以电网电压vsa定d轴方向,则vq=0。假设各子模块直流链电压均衡,vdc为直流链电压平均值。
对于直流链电压动态模型,由于虚拟系统直流侧并不能对实际电路注入电流,因此直流链电压动态取决于原CHB系统直流输出电流idci以及IBDC直流输入电流iLi,其动态方程为[12]:
(4)
式中:i=1,2,…,N;hi为第i个H桥整流单元的开关函数;fs为IBDC开关频率;Di为第i个IBDC电路移相比,-1 根据式(3)、式(4)所示PET-BESS模型,系统基本控制策略为:CHB整流级采用基于dq坐标系的主动定功率控制,调节网侧有功/无功功率及正弦电流波形;IBDC级为被动功率控制,通过移相调节控制直流链电压稳定而跟踪CHB级功率。本节首先给出CHB控制器的设计,然后第2节详细介绍基于HPWM的电池均衡方法的原理及实现,对于IBDC直流链电压控制器,将在第3节阐述。 (5) 式中: 设新的控制量v=[v1,v2]T,并令式(5)等号右端等于v,可得到Brunovsky标准线性系统形式为: (6) 将式(6)代入原仿射系统(式(5)),易求得状态反馈控制律为: u=-N-1(Mx+b-v)= (7) 新线性系统控制量v采用比例—积分(PI)控制: (8) 式中:kp和ki分别为PI控制器的比例和积分系数;xref为状态变量x的参考值。 将式(8)代入式(6),可得并网电流闭环传递函数为: (9) 当BESS电池单元SOC不均衡时,需令各级联H桥不同步充放电,以使电池SOC趋于一致。因交流侧为同一并网电流,需控制各H桥单元的交流电压不同。SHE-PWM[13]方法通过调节各级联H桥触发角来实现链式BESS的差异化充放电,但低频相控的方式不仅使系统总有功功率调节范围变窄,其交流谐波特性及动态调节能力也较差。 基于CPS调制及对各单元调制波进行偏移修正的方法可不影响系统总运行功率,但由CPS谐波消除机理[20]所决定,各单元调制波含偏移会使各单元交流输出的较低次载波边带谐波不能完全抵消,无法实现等效开关频率提高N倍的效果。根据五模块CHB仿真结果显示(载波比为40,采用单极倍频调制),当各调制波含±10%的偏移量时,总交流输出含有80,160,240,320等次数的边带谐波,其中80次边带谐波含有量达到基波的3.7%,总谐波畸变率(THD)为15.06%;而调制波不含偏移时,则不含次数低于400次的谐波,THD仅为13%。 针对差异化充放电的目标,本文采用混合阶梯波及高频PWM的HPWM方法,不会影响系统总传输功率,在各模块不均衡充放电的同时仍具有良好的谐波特性[21]。此外,各单元功率不仅可实现大小的调节,其方向也可调节,有助于提高电池单元SOC的收敛速度。 在阐述HPWM原理之前,首先给出H桥开关模式与输出电平的对应关系,如附录A表A1所示:各H桥单元4个开关管采用同一桥臂两管互补导通的方式,当S1和S4导通时,模块电压为+vdc,输出+1电平,S2和S3导通时,模块电压为-vdc,输出-1电平,当S2和S4(或S1、S3)导通时,输出0电平。 HPWM多电平调制基本原理如附录A图A2所示,其本质上是基于波形合成原理,利用N-1个H桥模块工作于阶梯波模式,输出阶梯波电平ustep,剩下的一个模块工作于高频PWM模式,且其调制波为总调制波da与前N-1个模块输出的阶梯波之差,因此最终N个模块总的交流输出多电平波形不含低次谐波,只含有与PWM载波有关的谐波[21]。 本文中为加快电池SOC收敛速度,对工作于阶梯波模式的N-1个H桥模块只设置“+1”或“-1”开关模式,不设置“0”模式(零功率),使其相连接的电池单元非充电即放电;而工作于PWM模式的模块则按照调制波与三角载波的比较关系,可输出“+1”“-1”“0”这3种电平,以补偿阶梯波与所期望输出多电平正弦PWM波之差。 基于HPWM的SOC均衡策略可描述如下。 首先,将CHB控制器输出的总调制波da进行取整运算,计算当前时刻合成多电平波形的电平数k为: k=floor(|da|)+1k=1,2,…,N (10) 式中:floor(·)表示向低取整函数。 因已知每一时刻有N-1个模块工作于阶梯波模式,则可根据模块数N、当前k值以及da极性确定工作于“+1”和“-1”模式的模块数目,见表1。 表1 工作于阶梯波模式的模块数及输出阶梯波电平Table 1 Number of modules operating in step wave mode and output step wave level 表1中,m+1为每时刻工作于“+1”模式的H桥模块数目,m-1为每时刻工作于“-1”模式的H模块数目,任意时刻二者之和为N-1,ustep为该N-1个模块输出电平的总和。任意时刻,剩下的一个模块工作于PWM模式,其调制波ut为da与ustep之差,其表达式为: (11) 然后对各子模块电池单元的SOC值进行排序,并根据其SOC值的高低及总功率流向,对应选择各模块H桥的开关函数,具体为:在总功率为充电功率时,即da与ia同极性,在da正(负)半周令电池SOC较低(高)的m+1个H桥单元工作于“+1”开关模式,使电池充电(放电),而令SOC较高(低)的m-1个H桥工作于“-1”开关模式,使电池放电(充电)。同理,在总功率为放电功率时开关函数的确定与总功率充电时相反。任何时刻令SOC值位于中间的一个模块工作于PWM模式。 根据上述规则,附录A图A3给出了总功率为充电功率时一个工频周期内各模块开关函数的分布图,其中h1至hN表示电池SOC按由低到高顺序排列的H桥的开关函数。可见,该HPWM方法可保证在总输出多电平电压以及总功率不变的情况下,使SOC高的电池单元放电、SOC低的电池单元充电,最终实现所有模块电池的SOC趋于一致;且基于HPWM的SOC均衡控制与CHB功率控制相互独立,SOC估计的准确度和延时对系统功率控制环没有影响。此外,虽然HPWM运行时一相链路上各模块有充电、有放电,但任何时刻每个模块的交流电压最大为+vdc,最小为-vdc,或为平均值位于+vdc和-vdc之间的PWM波,不会出现部分模块承受超过系统额定电压应力的问题。 第2节表明,各H桥开关函数hi由电池单元SOC的大小及HPWM算法而确定,是非线性时变的,且随网侧功率指令的变化,CHB输入直流链的电流也变化。因此,对含直流链的IBDC而言,前级H桥整流电路是一个严重的非线性时变负载。 图2 IBDC级控制框图Fig.2 Block diagram of control in IBDC stage 图2(a)中IBDC控制器采用单电压环PI控制,环路简单,与电压、电流双闭环控制相比,不需要高频电流传感器,可节约系统成本。图中:kvp和kvi分别为直流链电压PI调节器的比例和积分系数;GIB为IBDC输入直流电流iLi对移相比Di的小信号传递函数,由式(4)第二式可计算得: (12) 式中:D*为稳态移相比值。 为抑制开关函数及功率指令变化对直流链电压波动的影响,本文提出IBDC协调控制策略,引入CHB开关函数及功率指令前馈,如图2(b)所示。 1)开关函数hi对直流电压的扰动分析 传统控制: (13) 协调控制: (14) 根据式(13)、式(14)可画出两种控制下直流链电压对开关函数hid的扰动波特图如图3所示(按照仿真部分所列参数绘图)。 图3 传统控制和协调控制开关函数扰动波特图Fig.3 Bode plots of switching function interference of conventional control and coordinated control 如图3所示,所提协调控制策略下的扰动幅值增益远小于传统控制下的扰动幅值增益,表明协调控制对开关函数扰动具有较强的衰减作用,使直流电压的波动减小。 传统控制: (15) 协调控制: (16) 此外,由于单相并网系统存在固有的二倍频波动问题,可在直流链电压反馈以及前馈支路中加装二次陷波器,以避免二倍频分量引入IBDC控制环[22]。 为了验证本文所提控制策略的有效性及优越性,采用MATLAB/Simulink软件搭建图1所示的PET-BESS,仿真模型参数如附录A表A2所示。此外,电池参数为300 V/28 Ah;CHB整流级控制参数为kp=560,ki=140 000;IBDC电压环PI参数分别为kvp=0.008 1,kvi=0.065 2。 仿真条件为:5个电池单元的SOC初始值分别设置为80.3%,80.15%,80%,79.85%,79.7%;双向有功功率指令Pref以0.4 s为时间间隔在833 kW与-833 kW间进行切换,无功功率指令为0。 图4给出了本文控制策略下PET-BESS系统的部分仿真结果。图4(a)为功率波形包括网侧有功功率P、无功功率Q以及电池功率Pbat,可看出网侧有功/无功功率对其指令的跟踪效果较好,电池功率可快速跟踪网侧有功功率P,由于电路损耗,其数值略小于P;图4(b)为电池单元SOC曲线,结果显示在0~0.25 s总功率为充电过程中,1号电池单元放电,其SOC下降,其他电池单元充电;在0.4~0.7 s总功率为放电过程中,5号电池单元充电,其他电池单元放电,最终5条SOC曲线逐渐收敛,该结果与第2节HPWM电池均衡策略的分析相符合。 图4 所提控制策略下的PET-BESS仿真波形Fig.4 Simulation waveforms of PET-BESS under the proposed control strategy 附录A图A5为IBDC采用不同控制策略时的直流链电压波形对比,可见,当IBDC采用所提协调控制策略时,直流链电压稳态纹波约为5 V,功率扰动时动态最大波动为10 V,均约为IBDC传统控制策略下的一半。该结果表明在所提IBDC控制器下,直流链电压稳态纹波及功率扰动时的动态波动均得到了有效抑制。 附录A图A6—图A8分别给出了整流级各H桥模块的交流电压vh1至vh5、直流输出电流idc1至idc5以及传递功率P1至P5的波形,显示了对应模块充放电差异化的电压、电流及功率特性。 本文PET-BESS由于包含IBDC级,中间直流电压由IBDC控制,因此在电池允许工作电压范围内,对CHB电流环没有影响;而当电池电压过低时,则应由上层能量管理系统(EMS)给PET控制器下达功率指令,限制输出功率或对电池组进行充电。 搭建小功率五模块级联PET-BESS实验平台,如附录A图A9所示。控制器采用数字信号处理器(DSP)+现场可编程门阵列(FPGA)架构,DSP28335主要实现控制算法,FPGA采用Xilinx XC3S400芯片,负责采样、通信和PWM脉冲生成。 实验参数为:电网电压vs有效值为200 V(50 Hz),额定功率P=2 kW,电池单元采用阀控式铅酸蓄电池,电池参数为60 V/28 Ah,直流链电容为20 mF,直流链电压参考值为60 V,受实验室条件限制,IBDC高频变压器变比为1∶1,而在实际BESS应用中,应根据需求设计合适的变比。其他参数与仿真参数一致。 由于实验条件限制,无法实时测量电池组SOC值,因此实验中采用测量电池电压的方法代替电池单元SOC值,以验证基于HPWM的电池均衡控制策略。 图5给出了在总功率为800 W时,各H桥输出交流电压vh1至vh5及多电平电压van的波形细节,同时给出网侧电流作为参照,由于测量关系,图中电流波形为流向电网侧的电流,即为-ia。可以看出,第1,3,5个H桥单元工作在电池充电模式,因其交流电压在半个工频周期内与-ia极性相反,即与ia极性相同;而第2个和第4个H桥在每半个周期既有正电平又有负电平,表明这两个H桥在充放电模式间交替运行。该结果与第2节中阐述的HPWM电池均衡算法相符合。此外,5个模块合成的多电平交流电压波形为11电平PWM波,波形质量较好,其THD为13.52% 。 图5 各模块交流电压及合成多电平电压波形Fig.5 Waveforms of AC voltage of each module and synthesized multi-level voltage 附录A图A10所示为有功功率从800 W切换至-800 W时电网电压vsa、并网电流ia以及交流多电平电压van的实验波形,可见稳态时并网电流正弦且单位功率因数运行,其THD为3.27%,电流动态调节过程不超过0.02 s,能够快速跟踪指令值。 附录A图A11为本文控制策略下直流链电压波形,结果显示5个模块直流链电压均衡稳定,稳态纹波不超过2 V,功率翻转时刻电压突降1.5 V,经0.1 s即可恢复,验证了IBDC直流链电压控制策略具有较好的控制品质。 附录A图A12给出了IBDC电路的一些变量波形,为电池充电模式下的结果,可看出IBDC高频变压器原边交流电压vpr1超前于副边电压vsec1一个小相位角,使得漏感电流iL1为充电电流。 附录A图A13绘出了5个电池单元的电压曲线变化图,由充电到放电过程中,5条曲线逐渐收敛,最终均衡,验证了本文中HPWM电池均衡策略的有效性。需要注意的是,由充电到放电切换时,所有电池电压均出现一个较大的电压降落,这是因为电池单元的内阻较大。 本文对基于级联H桥及IBDC拓扑的PET-BESS进行研究,提出基于HPWM多电平调制的电池均衡及协调控制策略。利用HPWM方法各子模块功率可双向非均衡分布的特点,进行电池单元的差异化充放电,可在保证总功率满足指令要求的同时实现电池SOC快速均衡。将CHB开关函数及功率指令作为前馈,提出IBDC直流链电压协调控制方法,可有效抑制直流链电压波动。 本文PET-BESS可在较低开关频率下输出良好的交流多电平电压,模块级联结构及IBDC优越的电压变换和电气隔离功能,使电池组的配置更灵活,对大规模储能系统的开发和应用有一定的参考价值。而对于级联式PET-BESS,下一步还需对其二倍频波动的抑制问题进行深入研究,以减少电容容量,提高系统功率密度。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。1.2 系统基本控制策略及CHB控制器





2 基于HPWM的电池均衡策略

3 IBDC直流链电压协调控制策略

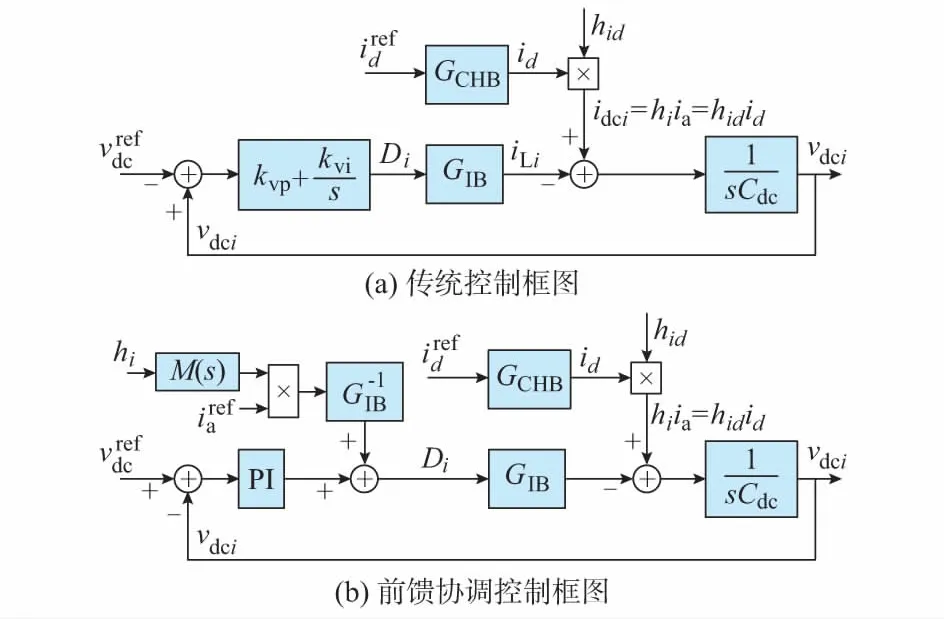


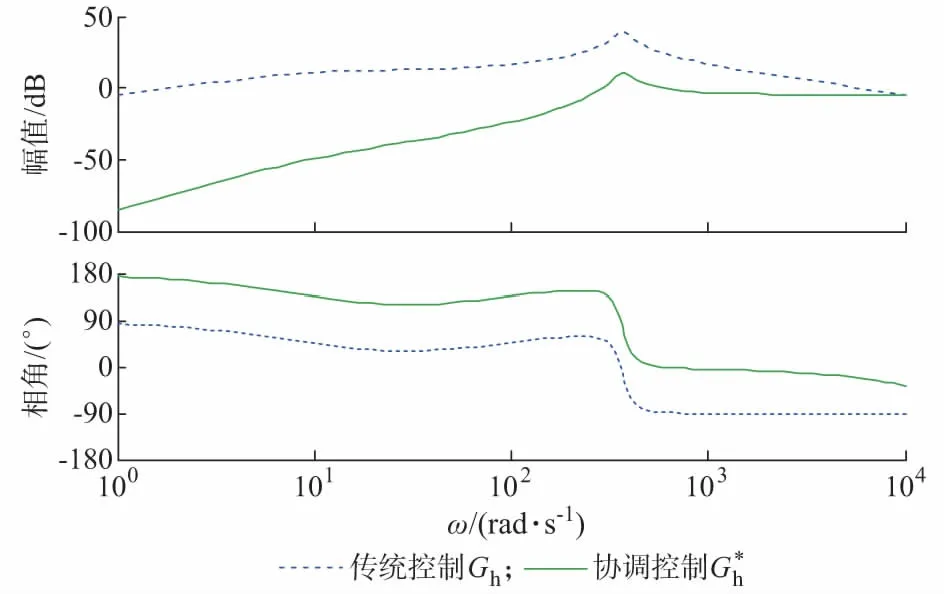


4 仿真分析及实验验证
4.1 仿真分析

4.2 实验验证
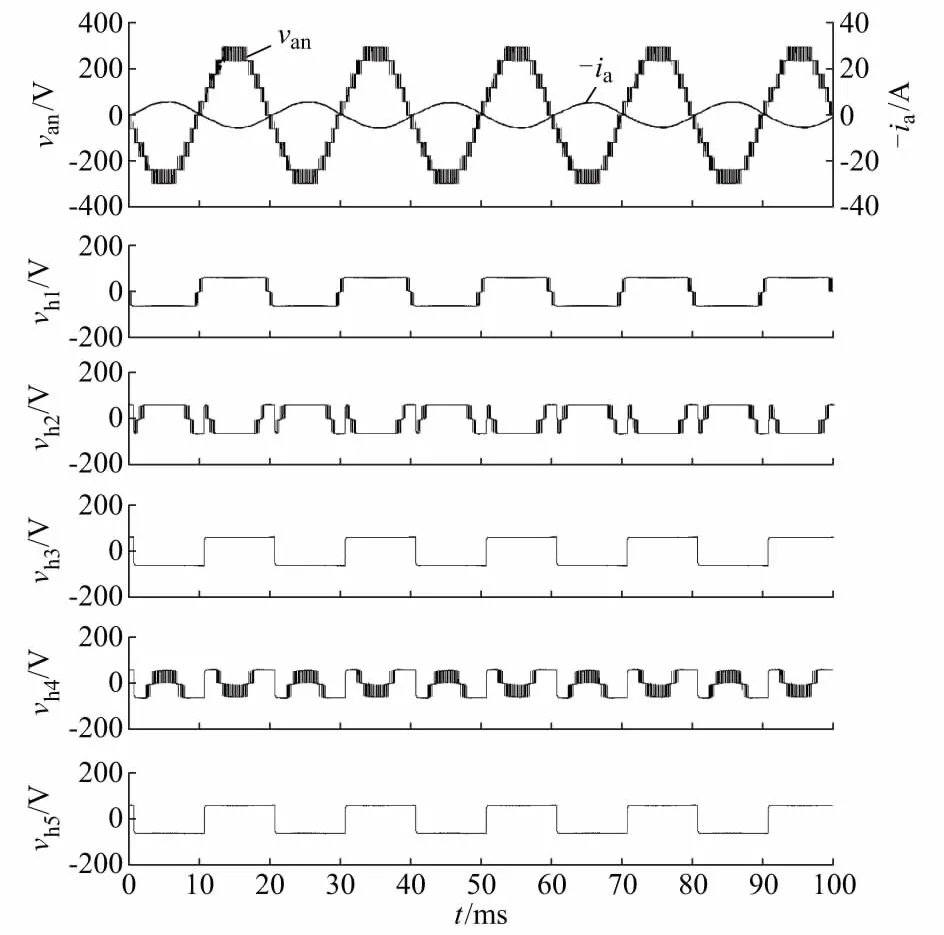
5 结语
