即插即用微电网集群分布式优化调度
2018-09-27周晓倩
周晓倩, 艾 芊, 王 皓
(上海交通大学电子信息与电气工程学院, 上海市 200240)
0 引言
为了有效解决大量分布式能源并入电网的难题,微电网[1]应运而生, 其依靠有效的能量管理整合各类分布式能源、负荷和储能设备,同时不同地域的毗邻微电网之间可以互相连接以形成微电网集群(MGC)。具体来说,MGC至少包含2个微电网单元,微电网单元之间是相关的,即有一定的相似性或互补性。而且,对于集群中任意一个微电网单元,在集群中至少存在另一个微电网单元与之互联。MGC可以和大电网进行能量交换,运行在并网状态,也可独立运行[2-3]。当MGC运行在并网状态时,子微电网的孤岛运行、并网运行分别对应从MGC中拔出、插入MGC,即子微电网的即插即用,其在工程应用中具有一定意义。
目前国内外对于MGC方面的研究相对较少,其中对于集中式优化,文献[4]采用全景理论研究多微电网之间的聚合优化运行;文献[5]针对孤岛型的MGC,利用最新的潮流计算对分布式电源的出力进行了优化;文献[6]采用改进的粒子群算法对海岛多微电网进行了动态调度。然而实际情况下,MGC问题属于大规模的优化问题,在集中式调度中心内统一处理将面临求解困难、易受中央系统故障以及其他通信故障的影响,同时由于子微电网之间的运行主体不同,在当今越来越重视隐私的时代,集中式协调优化将变得越发困难。分布式优化的出现将有助于解决这些难题,例如:文献[7]采用了一致性算法和原—对偶次梯度算法解决了智能电网的分布式优化问题,然而其采用完全分布式的方式,所需迭代次数过多;文献[8-9]同样采用次梯度算法最小化运行成本,其对离网子微电网之间的市场交易问题进行了分布式迭代求解。然而其仅将整个微电网成本等效为二次型函数,忽略了储能系统的成本优化,且仅考虑了单步优化;文献[10]基于交替方向乘子法对互联的微电网系统进行分布式优化调度,然而其集中调度中心虽不参与优化计算,在迭代公式中却需要各个子微电网的期望交换功率以计算出平均期望交换功率。由于集中调度中心的存在,将其称之为“伪分布式”。文献[11]针对灵活拓扑结构的MGC,设计了即插即用的分层框架,上层负责分布式求解子微电网与大电网之间的期望交换功率,下层负责集中式求解各个分布式能源的出力,然而其上层所需迭代次数已经达到了上万次,且收敛性不好。文献[12]针对互联的微电网采用二阶收敛的分布式牛顿法,显著地提高了优化问题的收敛速度,其将每个微电网的运行成本等效于其与大电网交互功率的函数,在满足各个微电网交互功率之和等于大电网调度命令约束的情况下,使用分布式牛顿法最小化整个集群的运行成本,然而这种等效并不具有适用性。除此之外,文献[11-12]仅考虑各个子微电网共同连接到微电网群母线,然后由群母线通过公共连接点(PCC)连接大电网的电气拓扑结构,然而实际情况下的MGC具有更复杂的电气拓扑形式,由于距离问题其内部之间经常互联,然后由1~2个离大电网较近的子微电网通过各自的PCC和大电网进行能量交互。
鉴于上述问题,本文针对相对复杂的大型互联微电网电气拓扑结构,提出了以拉格朗日乘法子为迭代变量和一致性变量,基于多反一致性和模型预测控制(MPC)[13-14]的分布式优化框架。具体来讲,该框架允许子微电网采用集中式优化以便于处理离散变量,子微电网之间采用分布式迭代以消除MGC集中调度中心的必要性。对应互联子微电网之间交互变量的拉格朗日乘法子数值相等,符号相反,且MGC中存在数个不同数值的乘法子,因此本文称之为多反一致性。
1 MGC的拓扑结构
本文所研究的MGC具有高的可再生能源渗透率,大约占比50%,且包含6个子微电网,每个子微电网之间可以通过配电网中广泛使用的光纤、无线或者电力载波等方式通信。因此,每个子微电网之间可以就近使用现有的通信线路,并不需要重新铺设通信线路。
如图1所示,每个子微电网均配备有一个智能体(Agent),负责采集当前的储能状态,运行本地优化程序,和邻居智能体交换当前交互变量迭代值以及下发最优控制命令。其中,各个子微电网之间的交互迭代过程与本地优化程序交替运行,即在给定交互变量初始值的条件下,子微电网以本地效益函数最小为优化目标,计算出目前迭代下的交互变量值并采集邻居的对应交互变量值和拉格朗日乘法子值,然后根据多反一致性迭代公式,计算出下一次迭代所用的拉格朗日乘法子,循环往复,直到拉格朗日乘法子的数值不再改变为止。值得说明的是,每个智能体仅和邻居智能体交换信息以便完全消除集中式调度中心的必要性。
2 MGC的数学模型
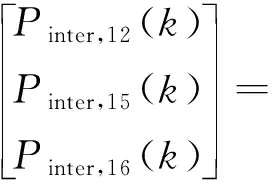
附录A图A1给出了每个子微电网的详细数学模型。以子微电网M1为例,根据能量平衡方程,可以得到其数学模型为:
Pinter,12(t)=-Paux,11(t)-P1Ed(t)-P1Ec(t)-
P1W(t)+PL11(t)
(1)
Pinter,15(t)=Paux,12(t)
(2)
Pinter,16(t)=P1MT(t)-Paux,11(t)-Paux,12(t)
(3)
式中:Pinter,12(t),Pinter,15(t),Pinter,16(t)分别为子微电网M1与M2,M5,M6之间t时刻的互联功率值;Paux,11(t)和Paux,12(t)为t时刻用于子微电网M1建模的辅助变量;P1Ec(t)和P1Ed(t)分别为t时刻子微电网M1中储能的充、放电功率;P1W(t)为t时刻子微电网M1中风机的功率;PL11(t)为t时刻子微电网M1中负荷的功率;P1MT(t)为t时刻子微电网M1中微型燃气轮机的功率。

图1 MGC的拓扑结构Fig.1 Topology of microgrid clusters
蓄电池的容量可以表示为:
(4)
式中:E1(t)为t时刻子微电网M1中的蓄电池容量;ηc和1/ηd分别为蓄电池的充电和放电效率。
式(1)至式(4)所表示的数学模型可以重新描述为状态空间模型。通过设置采样间隔,例如1 h,连续的状态空间方程能够被离散化,以设定的采样间隔执行优化程序[15]。如果把k作为优化时刻,离散化的状态空间模型可以表述为式(5)至式(7)。
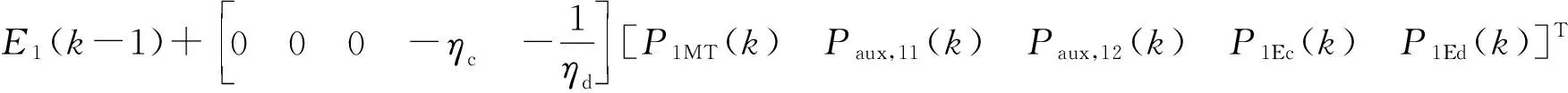
(5)
(6)

(7)
式中:Finter,ij(i=1,2,…,6;j=1,2,…,6;i≠j)为子微电网Mi与Mj之间的互联变量。
式(5)、式(6)、式(7)分别可改写为x1(k)=x1(k-1)+a1u1(k),y1(k)=b1u1(k)+c1w1(k),F1(k)=d1y1(k)。其中,x1,u1,w1,y1分别为状态变量、输入变量、扰动变量和输出变量;F1为子微电网之间的互联变量;a1,b1,c1,d1为对应向量的系数矩阵。
对剩余的子微电网应用相同的建模方法,可以得出M2~M6的对应向量和系数矩阵,如附录A表A1所示。
如式(5)至式(7)所示,本文的MPC分为状态变量、控制变量、扰动变量、输出变量[16]。其中状态变量是和上一时刻值有关的方程,这里只有储能的容量值是和上一时刻值有关,每个优化时刻均采集实际的储能容量值进行校正;控制变量就是待求的各个机组的出力;扰动变量就是风光负荷等的预测信息;输出变量就是互联功率变量。假设当前时刻系统正在运行,那么目的就是在已知风光负荷等未来时刻预测值的基础上,利用MPC框架,考虑未来的一段预测时域,求解出下一时刻不同机组以及储能的出力值,当下一时刻到来时,又开始重复此过程。
3 基于多反一致性和MPC的分布式优化框架
3.1 增广的拉格朗日函数
通过增广的拉格朗日描述(augmented Lagrange formulation,ALF),可以将集中式的优化问题分为相应的子问题求解,文献[17-19]详细给出了ALF的使用方法和聚合性分析。在增广的拉格朗日函数中,每一个智能体的本地效益函数不仅包括本地成本函数,还包括和互联约束(8)相关的互联函数。
Finter,ij(k)=Finter,ji(k)i=1,2,…,nN;j∈Ni
(8)
式中:Ni为子微电网Mi的邻居集合;nN为子微电网的个数,本文取为6。
为了实现将MGC集中优化问题分解到各个本地子问题,互联约束(8)被写入增广的目标函数中,如下所示:
φaug(X(k),U(k),Y(k),T(k),Λ(k))=
(9)
(10)
式中:φlocal,i(xi(k),ui(k),yi(k))为子微电网Mi的本地成本函数;ρ为惩罚因子,用来凸化目标函数;λinter,ij(k)为子微电网Mi和邻居子微电网Mj(j∈Ni)之间互联相关的拉格朗日乘法子。
根据对偶理论[20],式(9)能被分解为几个子问题,每个子问题(本地效益函数)可以分配给对应的本地智能体执行,不失最优性的分配原则请参考文献[21],其中提出采用“辅助问题原则(auxiliary problem principle,APP)”进行分布式分解计算。即

yi(k))+φinter,i(Fi(k)))
(11)
式中:φAgent,i为分配给智能体i(对应子微电网Mi)执行的本地效益函数;φinter,i(Fi(k))为子微电网Mi的互联函数。
每个子问题式(11)以迭代的、平行的方式执行,具体来讲,在每一次迭代中,每个智能体以集中式的方式平行地求解对应的子问题,然后将目前迭代步骤下的求解结果(互联变量、拉格朗日乘法子)和邻居智能体相互交换,更新下一次迭代所用的拉格朗日乘法子。
3.2 基于MPC的本地效益函数
式(11)给出了本地效益函数的简单表述形式,其分为本地成本函数和互联函数,具体见式(12)和式(13)。特别地,本文考虑互联变量的惩罚因子以调节本地资源被消耗的程度。
(12)
(13)

3.3 基于多反一致性的分布式迭代
基于多反一致性的分布式迭代公式如式(14)和式(15)所示。

j∈Ni
(14)
(15)

分布式迭代流程图如图2所示,具体的迭代步骤描述如下。
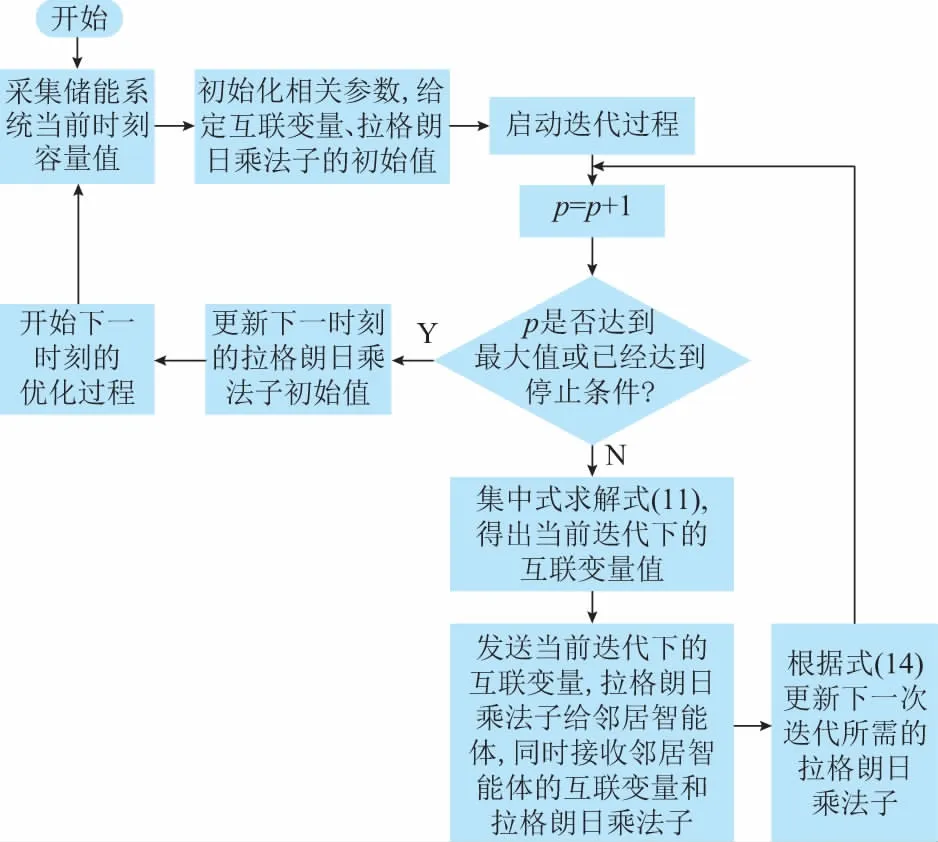
图2 分布式迭代流程图Fig.2 Flow chart of distributed iteration
1)采集储能系统当前时刻的容量信息。



8)开始下一时刻的优化过程。
本文取ρ=wij=0.3。一方面参照文献[21](其首次提出依据APP方法的分区域互联系统的分布式优化方法)附录部分证明的全局达到最优的参数ρ的最小取值(ρ≥wij)以及所给经验值ρ=2wij;另一方面做了大量的仿真实验,并与集中式二次规划方法做了对比。
其中,每个子微电网φAgent,i最优是在满足功率平衡约束(MPC框架自带功率平衡约束)、互联功率约束以及子微电网之间协调(一致性算法(式(14)))基础之上达到的最优,而并非独立意义上的最优,且与子微电网之间协调式(14)有关的互联效益函数式(13)包含有全局最优聚合常数ρ。由文献[22]可知,当目标函数是凸的,约束是仿射的,由平行的、迭代的方式得出的子问题的解是最优的,和集中优化问题的解相同。由于子微电网i的本地效益函数式(11)以及集中优化问题式(9)均满足凸假设,互联约束式(8)以及之后的蓄电池约束、MPC框架约束和机组爬坡率约束均是仿射的,当ρ的取值满足最小取值要求且足够小时,通过各个子微电网本地效益函数式(11)最优以及子微电网之间的协调不断迭代可以使全局快速达到最优,即和MGC集中优化问题式(9)的解相同。
4 运行约束
本文考虑蓄电池约束、MPC框架约束以及机组爬坡率约束,其中蓄电池约束被包括在MPC框架约束中,分别如式(16)至式(18)所示。
(16)
(17)
i=1,2,…,5
(18)

式(19)给出了MGC的实际运行成本,即
(19)
式中:φresult,i(k)为子微电网i在k时刻的实际运行成本;φresult(k)为k时刻的MGC实际运行成本;Qaux,i为去除惩罚因子fc后的实际成本矩阵。
5 仿真结果和讨论
5.1 聚合性
算例在MATLAB中,使用Gurobi商业求解器求解。每个智能体均以1 h的时间间隔执行式(11),最终得出24步的优化结果。在误差限制ε=0.001之内,得出每个时刻的所需迭代次数以及优化误差,如图3所示。从图3可以看出,每个优化时刻MGC均能在少量迭代内达到聚合。

图3 优化误差与迭代次数Fig.3 Optimization error and iteration times
附录B图B1(a)至(c)分别给出了K=1时刻微电网成本、拉格朗日乗法子以及互联变量的聚合过程。从图B1中可以看出,MGC在40次迭代时均已聚合,拉格朗日乗法子数值相等、符号相反,呈对称状态,证明了前述多反一致性的假设。同时,互联功率相等,MGC达到最优状态。
5.2 即插即用
附录B图B2(a)至(c)分别给出了K=1时刻子微电网5在迭代前拔出、在迭代前拔出且在100次迭代时恢复、在70次迭代时拔出且150次迭代时恢复的聚合过程。对比图B1(a)与图B2(a)的结果可知,子微电网5在未拔出时,其基本不出力,所需要的功率由子微电网6提供;在子微电网5拔出后,其内部所需功率由自身提供,成本增加,而对应的子微电网6成本则降低。同样的,从图B2(b)可以看出,在100次迭代时子微电网5重新插入后,其内部成本又迅速降为0,对应的子微电网6的成本快速增加,MGC又重新达到新的平衡。子微电网5连续的拔出插入过程如图B2(c)所示,在70次迭代子微电网5被拔出且150次迭代子微电网5被重新插入后,MGC均能快速响应,每个改变过程,在短的时间内达到新的平衡,从而证明了本文所提方法对MGC即插即用的有效性。
5.3 预测时域
附录B图B3分别给出了有、无自适应调度时不同的预测时域对结果的影响。从中可以看出:当无自适应调度时,预测时域的变化对结果影响很大,总的趋势是预测时域N越小,MGC实际成本越高,反之,则越低;当有自适应调度时,预测时域的变化对结果的影响不明显,这是由于自适应调度减少了后续时刻的影响所致。通过图B3,进一步证明了本文所提MPC方法的有效性。
5.4 惩罚因子
附录B图B4给出了不同惩罚因子、不同优化时刻储能容量的变化曲线。从中可以看出:在惩罚因子较小(0.5)时,储能容量的变化趋势基本相同;当增大到1.5时,子微电网1,3,4,5的储能容量发生了较大的变化,即充放电更深,这是由于较高的惩罚因子使得能源更多的在本地微电网消耗或吸纳所致;当惩罚因子更高为4.5时,子微电网之间的功率流动进一步减少,储能根据自身的容量配置以及本地能源配置在惩罚能力更强的情况下充放电运行。
附录B图B5给出了不同惩罚因子下的MGC运行成本,可以看出,惩罚因子越高,MGC成本越高。惩罚因子越低,子微电网之间的功率自由流动,MGC优先选择发电成本低的能源,因此成本大大降低。从图B4和图B5可以看出,本文提出的方法大大增强了MGC的灵活性。
5.5 最优性证明
为了说明本文所提分布式MPC方法与集中式二次规划算法所求取的结果基本相同,并方便给出每个机组的出力数据结果,本实例使用3个互相连接的子微电网,每个子微电网包含一个发电机(G1,G2,G3)和一个负荷(L1,L2,L3),其中G1发电成本二次项和一次项系数a1=0.036,b1=3.6;G2成本系数a2=0.038,b2=3.0;G3成本系数a3=0.053,b3=3.3,并取预测时域N=5,迭代次数pmax=250。图4给出了不同的ρ值下,K=1时刻下的发电机出力迭代结果,并与K=1时刻集中式求解的相应发电机出力做了对比。其中K=1时刻的负荷取值分别为L1=10 kW,L2=5 kW,L3=7 kW;附录B图B6给出了ρ=wij=0.3下24个点的发电机出力,并与集中式求解的24个点的相应发电机出力做了对比。

图4 不同ρ下发电机出力的迭代结果Fig.4 Iterative results of generators for different ρ
从图4可以看出,随着ρ值的增大,发电机的迭代出力结果发生了较大的变化,具体来说,当ρ值比较小(0.3,0.6,1,3)时,系统能在较小给定迭代次数内聚合于集中式求解结果,且随着ρ值的增大,聚合至最优值所需的迭代次数逐渐增加;当ρ值较大(5,10,20)时,系统已无法在给定迭代次数内达到聚合,其运行于次优状态;当ρ值足够大(10 000)时,各个子微电网自发自用,其出力值在给定迭代次数内保持收敛于子微电网内的负荷值,分别为10,5,7 kW。通过以上分析可知,通过设置比较小的聚合常数ρ,可以使系统快速聚合于最优值。
从附录B图B6可以看出,在每个优化时刻,分布式求解的结果均和集中式的相同,再一次证明了本文所提分布式模型预测可以收敛至全局最优值。
在K=1时刻,ρ=wij=0.3,预测时域N=1下,迭代次数分别为50,100,150,200时的每个智能体仿真所需要的时间分别为:64.47,110.58,177.56,242.31 s。仿真使用的是MATLAB2014a,个人计算机配置为Intel(R) Core(TM) i5-4200M,2.50 GHz主频。
从中可以看出,随着迭代次数的增加,仿真时间增加,大概每增加50次,仿真时间大约增加60 s。由于合适的聚合常数ρ可以使系统在50次内聚合,因此求取到最优解只需大约60 s。由于运行程序所用的电脑配置比较低,在高配的电脑上仿真时间会更短。
6 结语
本文提出了一种基于多反一致性和MPC的即插即用MGC分布式优化算法,通过该分布式算法,大规模复杂结构的MGC可以通过本地集中式优化、全局分布式迭代的方式进行快速能量管理。这种混合优化方式大大地增强了MGC的灵活性,同时保护了本地微电网的隐私信息。不仅如此,通过设置不同的辅助聚合常数,MGC可以实现灵活快速的即插即用。MPC作为一种最优控制方法,其考虑未来时刻的可能状态并对未来时刻产生影响的相关变量进行实时校正,以形成相关变量的闭环控制,增强系统的鲁棒性。因此,结合MPC的分布式迭代方法不仅可以去除集中调度中心,而且能够增强系统的抗干扰性能。最后,通过调节惩罚因子,本地微电网可以选择是参与集群运行还是减弱集群运行,从而赋予用户更多的选择权利。
本文的MPC框架已经将风光负荷等预测值作为系统扰动变量考虑了进去,下一步需要考虑风光负荷等不确定量的预测问题,也就是说减少预测误差对结果的影响。下一步拟将随机场景规划和本文所提分布式MPC框架结合,来进一步降低预测误差,提高调度精度。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
