垂荡板对浮式风力机平台动态响应的影响

2018-09-27丁勤卫郝文星周红杰

动力工程学报 2018年9期

余万，丁勤卫，李春，郝文星，周红杰，张凯

(1. 上海理工大学能源与动力工程学院，上海 200093； 2. 国家电投集团山东能源发展有限公司，济南 250002)

2017年2月全球风能理事会(GWEC)发布的《2016年全球风电统计数据》报告显示，2016年全球风电累计装机容量新增超过54.6 GW，全球累计容量达到486.7 GW[1]。相比于陆上风能资源，海上风能资源具有低湍流度的稳定风况以及不占用陆地资源等优点[2-3]。未来风电场建设的必然趋势是由陆向海，由浅到深，由固定基础向漂浮式平台[4]。浮式风力机基础平台有很多种[5-8]，其中Spar平台虽具有重心低、运动性能好、灵活度高和造价低等优点[8]，但在实际应用中存在一些问题，其自振频率与波浪主要频率接近时，极易发生共振现象，导致平台垂荡运动幅度过大，严重时则会引起系泊系统的破坏。为改善Spar平台的垂荡运动，必须采取一定措施使其自振频率避开波浪的主要频率范围。目前，改变Spar平台垂荡固有周期的方法有2种[9]：增大平台吃水深度和增大平台垂荡阻尼。其中，增大平台吃水深度会增大平台质量，从而导致平台建造费用增加。故国内外学者针对增大平台垂荡阻尼展开了诸多研究。Tao等[10]通过实验方法研究了振荡幅值、振荡频率和透空率对垂荡板水动力特性的影响。王言哲等[11]计算了附有垂荡板的Spar平台的黏性阻尼，得到考虑黏性阻尼的平台垂荡响应，并将其与Aqwa软件的计算结果进行对比分析。Subbulakshmi等[12]研究了不同垂荡板数目及其安装位置对浮式风力机Spar平台垂荡运动的影响。

针对垂荡板及其对平台水动力特性影响的研究主要侧重于以下方面：通过实验方法研究单块或多块垂荡板的水动力性能，未研究垂荡板对Spar平台水动力性能的影响，此外实验方法受限于设备的精度，结果准确性有待考证，如文献[10]和文献[13]的研究结果差别较大；通过数值计算方法研究垂荡板对平台水动力性能的影响，多侧重于传统海工石油平台[11,14]；针对浮式风力机Spar平台的研究大多为第一代Spar(Classic Spar)平台[12,15]。与Classic Spar平台相比，Cell Spar平台的水动力性能更优越，但基于Cell Spar平台的浮式风力机的研究很少。

因此，笔者借鉴石油平台的结构设计经验，基于Classic Spar平台概念提出一种新型Cell Spar平台，建立了基于Classic Spar和Cell Spar平台的2种浮式风力机整机模型，在考虑风波流载荷影响的情况下采用Aqwa软件求解得到2种平台的动态响应特性，并基于Cell Spar平台建立附加垂荡板的浮式风力机整机模型，研究垂荡板及其结构参数对浮式风力机Cell Spar平台动态响应的影响，以期为远海浮式风力机平台的结构设计、优化和安全性提供理论参考。

1 几何模型

用于深海钻探和采油工作的Spar平台已开发出3代类型[16]，如图1所示。

图1 3代类型的Spar平台

在图2(a)中增加Cell Spar平台的结构特点(垂荡板结构)，即可得到图2(b)。选用美国国家能源可再生实验室(NREL)的5 MW风力机。在Cell Spar平台中，采用6根直径为2.2 m的浮筒、1根直径为4 m的浮筒和3块直径为9.4 m、厚度为0.2 m的垂荡板替代OC3-Hywind Spar平台(以下简称Classic Spar平台)原主体部分。在Cell Spar平台中，采用Classic Spar平台[17]原有的系泊系统。

(a) Classic Spar平台(b) Cell Spar平台

图2 浮式风力机Spar平台

Fig.2 Spar platform of floating wind turbine

2 载荷计算

浮式风力机Spar平台作业环境极为复杂，受到海风、波浪、海流和地震等多种环境载荷作用。在已有浮式风力机研究中，主要考虑海风载荷[18]、波浪载荷[19]以及海流载荷[18]的作用，且假定风波流均以-180°的角度入射。

2.1 海风载荷

相对于深海勘探Spar平台，浮式风力机Spar平台因塔架结构高耸及其顶部风轮扫掠面积很大，因此受到更大的海风载荷作用。风力机风轮受到的海风载荷的计算方法主要有叶素-动量理论(BEM)方法、二维势流方法和计算流体力学方法，其中BEM方法简单有效。

浮式风力机正常工作时，根据BEM方法可以得到风轮受到的海风载荷Fw1：

(1)

式中：CT为轴向推力系数，取为8/9；ρa为空气密度，kg/m3；Aw为风轮扫掠面积，m2；V0为额定风速，m/s。

风力机停机时，作用在风轮上的海风载荷Fw2为：

(2)

式中：CD为空气阻力系数，一般取为1.1；S为所有叶片的面积之和，通常为Aw的5%～10%，m2；VE为风力机停机时的风速，m/s。

塔架所受到的海风载荷为：

(3)

式中：At为塔架上受风面的投影面积，m2；Vh(t)为海平面上高度为h处的瞬时速度，m/s。

2.2 波浪载荷

波浪运动是复杂的随机过程，在海洋学中采用波浪谱描述波浪运动，笔者采用的是适用于有限风区的JONSWAPS谱。

浮式风力机平台所受的水动力主要包括波浪激振力、结构运动产生的辐射力和考虑波浪高阶效应的漂移力，其中波浪激振力包括结构对波浪作用的绕射力和入射波形成的弗汝德-克雷洛夫力(K-F力)。对作用于浮式风力机Spar平台的波浪力，通常采用K-F理论和绕射理论进行计算。由于浮式风力机Spar平台波浪力求解的复杂性，故引入无黏性、不可压缩理想流体和无旋流体的假设，以简化波浪力的求解问题。入射波遇到平台结构时，会在其表面产生散射波，入射波与散射波相互叠加形成新的波动场，其总速度势为：

Φ(x,y,z,t)=ΦI(x,y,z,t)+ΦD(x,y,z,t)

(4)

式中：ΦI(x,y,z,t)为入射波速度势；ΦD(x,y,z,t)为散射波速度势。

总速度势在整个波动场内满足拉普拉斯方程和相应的边界条件，因此可求得总速度势。根据伯努利方程，结构物表面的压力p为：

(5)

式中：ρ为流体密度，kg/m3。

作用在平台上的波浪力F和波浪力矩M分别为：

F=∬s-pnds

(6)

M=∬s-p(r×n)ds

(7)

式中：n为平台表面的外法线矢量；r为平台表面2点的径向矢量；s为平台与波浪的接触面积。

2.3 海流载荷

在工程计算和设计中考虑海流速度变化缓慢，通常将海流作为稳定流动，认为海流对平台的作用仅为拖曳力。当仅考虑海流作用时，作用在平台水下部分的海流载荷为：

Fc=0.5CdρwAVc

(8)

式中：Cd为水阻力系数，取为0.7；ρw为海水密度，kg/m3；A为平台与海流垂直面上的投影面积，m2；Vc为海流流速，m/s。

3 Cell Spar平台频率分析

浮式风力机Spar平台在环境载荷作用下在6个自由度方向运动，如图3所示。其中，纵荡、横荡及垂荡为平台平动自由度，纵摇、横摇和艏摇为平台转动自由度，β为波浪入射角。由于定义海风、波浪及海流均以-180°入射，故仅需分析平台在纵荡、垂荡及纵摇3个自由度的运动。

图3 平台6个自由度

幅值响应算子(RRAO)表征单位波幅的特征响应，是平台运动谱与波浪谱的比值。图4为Classic Spar平台与Cell Spar平台在纵荡、垂荡及纵摇方向上RRAO的频域曲线。

由图4可知，在纵荡方向上，较之Cell Spar平台，Classic Spar平台的RRAO最大值较大，约为1.86，2种平台在RRAO峰值对应的纵荡运动频率相近；与Cell Spar平台相比，垂荡方向上Classic Spar平台的RRAO最大值较大，约为7.02，且其曲线峰值对应的波浪频率较小；与Cell Spar平台相比，纵摇方向上Classic Spar平台的RRAO最大值较大，约为13.45，且其曲线峰值对应的波浪频率较小。综上，Cell Spar平台频域曲线峰值对应的波浪频率较大，从而远离波浪集中的频段。因此，Cell Spar平台有更好的平台动态特性。

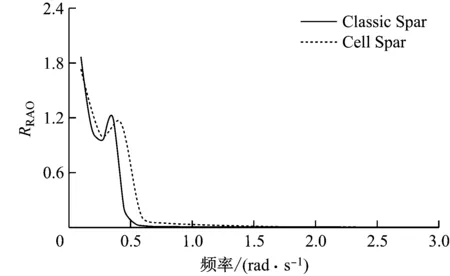
(a)纵荡

(b)垂荡

(c)纵摇

4 结果与分析

环境载荷参选东海25年一遇的极端海况，海风选用Ochi & Shin风速谱，平均风速为50 m/s；波浪选用JONSWAPS波浪谱，有义波高为11.2 m，跨零周期为11.9 s；将海流简化为均匀流，速度为1.5 m/s，水深取为320 m。基于上述环境载荷，研究垂荡板形状、厚度、数目和透孔率对Cell Spar平台动态响应的影响。

4.1 垂荡板形状

为研究垂荡板形状对平台动态响应的影响，以图2(b)所示的Cell Spar平台为基础，选取4种不同形状、当量直径均为9.4 m、厚度均为0.2 m的垂荡板为研究对象，如图5所示。

图6给出了附有不同形状垂荡板的Cell Spar平台在纵荡、垂荡和纵摇上的RRAO频域曲线。图7给出了附有不同形状垂荡板的Cell Spar平台在纵荡、垂荡及纵摇上的时域曲线。

图5 不同形状的垂荡板

(a)纵荡

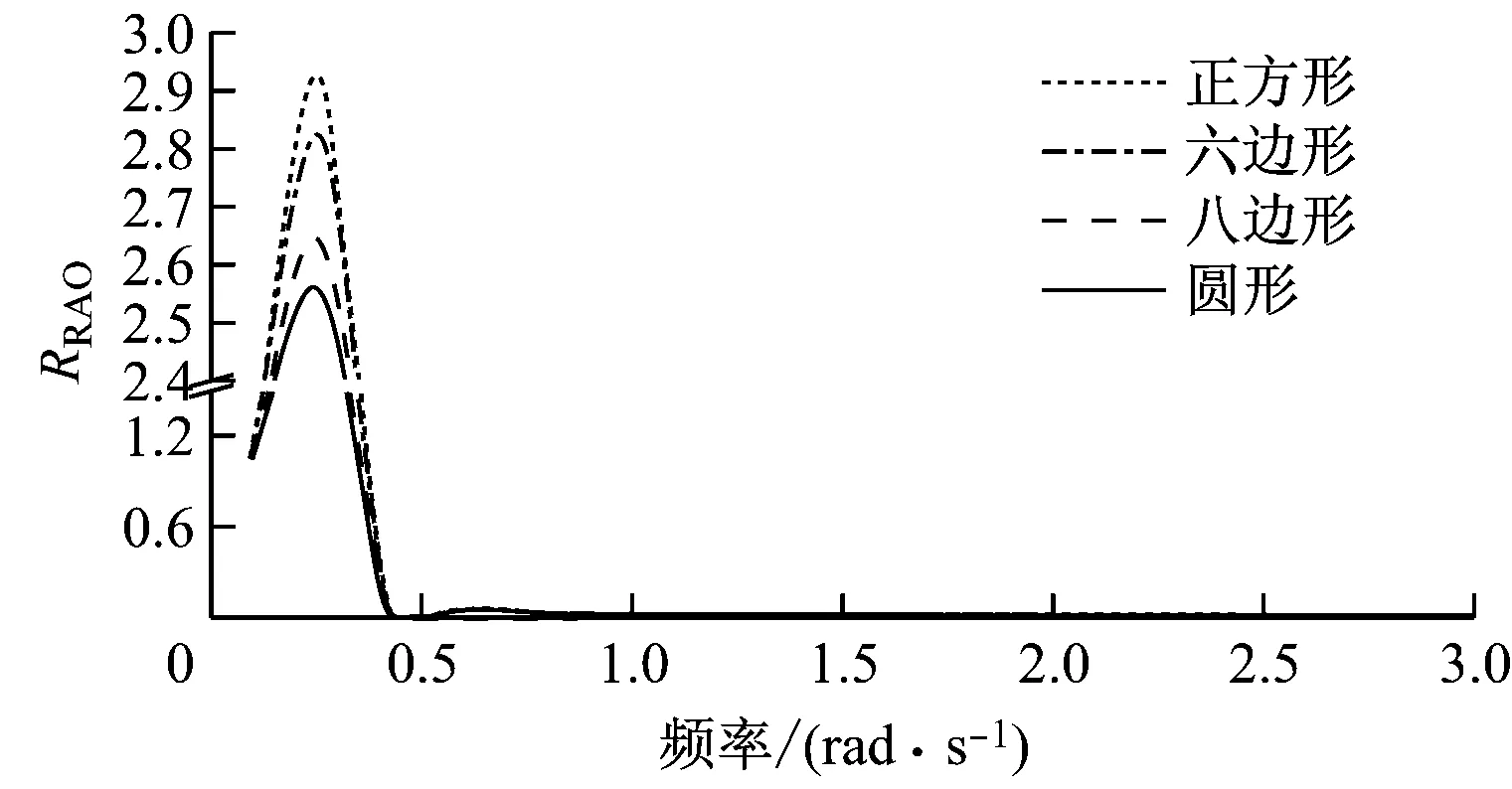
(b)垂荡

(c)纵摇

由图6可知，垂荡板形状不会影响曲线峰值对应的波浪频率，但会影响平台RRAO曲线峰值的大小；在3个自由度方向上，圆形垂荡板的平台RRAO曲线峰值均最小。由图7可知，垂荡板形状不会影响平台3个自由度方向上的运动周期；在纵荡方向上，圆形垂荡板的平台纵荡位移最小，六边形垂荡板的平台纵荡位移最大；在垂荡方向上，八边形、六边形和正方形垂荡板的平台时域曲线几乎重合，圆形垂荡板对平台垂荡运动的抑制作用最好；在纵摇方向上，圆形和正方形垂荡板的平台纵摇角度相似，八边形垂荡板的平台纵摇角度最大。

(a)纵荡

(b)垂荡

(c)纵摇

综上所述，与其他形状垂荡板相比，附有圆形垂荡板的平台动态响应最优，表明圆形垂荡板更利于平台稳定性。

4.2 垂荡板厚度

垂荡板厚度是垂荡板的重要结构参数，对垂荡板的性能有一定影响。为研究垂荡板厚度对平台动态响应的影响，选取具有不同厚度(0.10 m、0.15 m、0.20 m、0.25 m、0.30 m、0.35 m、0.40 m、0.45 m和0.50 m)、相同当量直径(9.4 m)的圆形垂荡板为研究对象。平台在纵荡、垂荡及纵摇方向上RRAO曲线峰值随垂荡板厚度的变化如图8所示。表1给出了不同厚度垂荡板的Cell Spar平台在纵荡、垂荡及纵摇方向上运动响应的幅值范围，其中“-”表示方向。

由图8可知，在各自由度上低频处平台RRAO曲线均出现了峰值，其中厚度为0.40 m、0.45 m和0.5m的垂荡板在3个自由度上的响应值非常接近，其差值在10-2的数量级。由表1可知，随着垂荡板厚度的增大，平台垂荡和纵摇运动幅值逐渐减小，但在厚度超过0.4 m时，幅值减小效果不明显；纵荡运动幅值无明显差异。考虑到垂荡板的经济性和运动稳定性，选取厚度为0.4 m的垂荡板时平台运动性能较优。

(a)纵荡

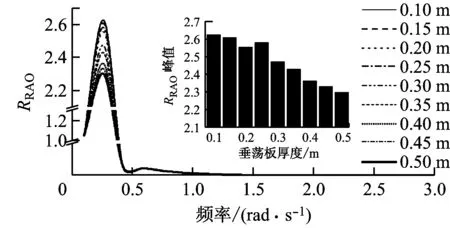
(b)垂荡

(c)纵摇

Tab.1Timedomainamplituderangeofplatformwithheaveplatesofdifferentthicknesses

厚度/m纵荡位移/m垂荡位移/m纵摇角度/(°)0.100.150.200.250.300.350.400.450.504.218.6019.40-4.20-8.49-19.104.418.5419.35-4.31-8.44-19.294.448.4319.47-4.35-8.36-19.494.458.4119.34-4.31-8.29-19.244.228.0818.37-4.15-7.98-18.244.297.9418.98-4.17-7.84-18.814.217.7418.19-4.07-7.64-18.424.177.6218.08-4.06-7.53-18.314.277.5218.52-4.04-7.43-18.92

4.3 垂荡板数目

为进一步研究垂荡板数目对平台动态响应的影响，在浮式风力机Cell Spar平台下部固定的42 m高度内分别放置不同数目的垂荡板，结构如图9所示。

(a)1块板(b)2块板(c)3块板(d)4块板(e)5块板(f)6块板(g)7块板(h)8块板

图9 不同数目的垂荡板

Fig.9 Structural diagram of the column with different number of heave plates

图10为平台在纵荡、垂荡及纵摇上RRAO曲线峰值随垂荡板数目的变化。表2为不同数目垂荡板的Cell Spar平台在纵荡、垂荡及纵摇方向上运动响应的幅值范围。

由图10可知，在纵荡方向上，附有8块垂荡板的平台RRAO峰值最大，附有1块垂荡板的平台RRAO峰值最小，两者差值为0.71；在垂荡方向上，随着垂荡板数目的增加，RRAO峰值逐渐减小，但减小趋势减缓；在纵摇方向上，附有7块垂荡板与8块垂荡板的RRAO峰值相近，且与RRAO峰值的最小值相差2.01 °/m。由表2可知，随着垂荡板数目的增加，平台垂荡运动幅值逐渐减小，而在纵荡和纵摇方向上平台运动急剧增大，故选取适合的垂荡板数目极为重要。综合考虑平台纵荡、垂荡及纵摇的运动和经济效应，选取4块垂荡板时平台运动性能较优。

4.4 垂荡板透孔率

对垂荡板进行开孔，其开孔面积与垂荡板面积的比值定义为透空率。基于以上研究，选取圆形垂荡板，其厚度为0.4 m，数目为4块。考虑5种不同透空率的垂荡板对平台动态响特性的影响，图11为5种透空率的垂荡板。

(a)纵荡

(b)垂荡

(c)纵摇

Tab.2Timedomainamplituderangeofplatformwithdifferentnumberofheaveplates

垂荡板数目纵荡位移/m垂荡位移/m纵摇角度/(°)123456783.2616.3915.73-3.58-16.18-15.883.8611.2317.68-3.91-11.09-17.634.448.4319.46-4.35-8.36-19.494.956.2320.59-4.79-6.14-20.635.325.5221.38-5.17-5.42-21.165.695.0922.18-5.49-4.98-22.196.484.6923.98-6.15-4.58-24.356.644.4724.26-6.24-4.36-24.95

图11 不同透空率的垂荡板

图12为平台在纵荡、垂荡及纵摇方向上RRAO曲线峰值随垂荡板透空率变化的曲线。表3为具有不同透空率垂荡板的Cell Spar平台在纵荡、垂荡及纵摇方向上运动响应的幅值范围。

(a)纵荡

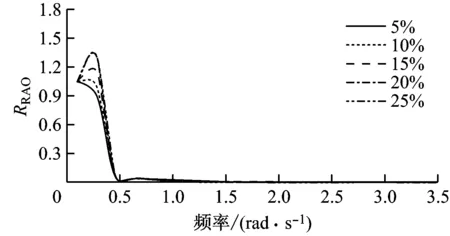
(b)垂荡

(c)纵摇

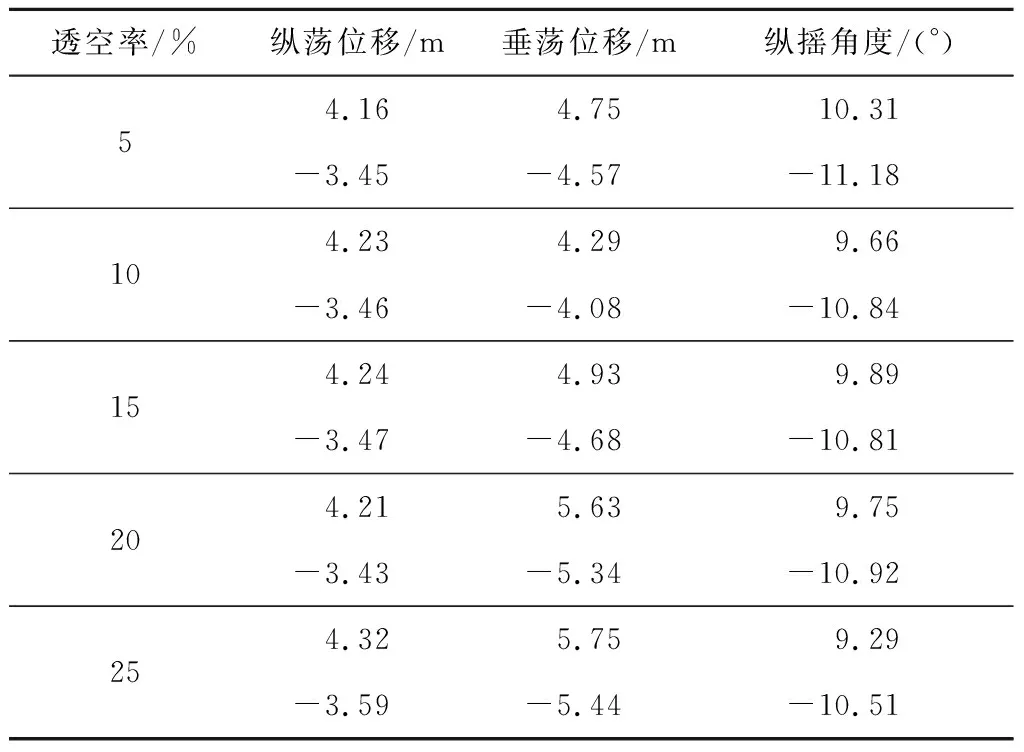
由图12可知，透空率对平台的纵荡RRAO没有影响；在垂荡方向上，随着透空率的增大，平台的垂荡RRAO峰值增大；在纵摇方向上，25%透空率垂荡板的平台RRAO峰值最小，与最大峰值相差约0.15 °/m。由表3可知，在不同透空率垂荡板下平台的纵荡位移幅值范围的差异很小；随着透空率的增大，平台的垂荡位移先减小后增大，纵摇角度大致呈减小趋势。综上，垂荡板透空率对平台纵荡及纵摇方向的影响较小，对垂荡方向的影响较大。根据平台时域幅值可知，选择透空率为10%的垂荡板较为合适。

表3不同透空率垂荡板的平台时域幅值范围

Tab.3Timedomainamplituderangeofplatformwithheaveplatesofdifferentpermeabilityrates

透空率/%纵荡位移/m垂荡位移/m纵摇角度/(°)5101520254.164.7510.31-3.45-4.57-11.184.234.299.66-3.46-4.08-10.844.244.939.89-3.47-4.68-10.814.215.639.75-3.43-5.34-10.924.325.759.29-3.59-5.44-10.51