基于DEKF联合估计的CD3S信号解调算法

袁国刚, 王永川, 陈 鹏, 高喜俊

(中国人民解放军陆军工程大学石家庄校区无人机工程系, 河北 石家庄 050003)

0 引 言

混沌信号的类噪声性、初值敏感性、非周期性及宽频谱特性使其在保密通信领域受到广泛关注[1-3]。混沌直接序列扩频(chaotic direct sequence spread spectrum, CD3S)通信用实值混沌序列代替传统伪随机扩频序列对信息码扩频,具有保密性高[4]和截获概率低[5]的优点。实值混沌序列为非周期非二进制序列,传统伪随机扩频码为周期二进制序列,这使得传统直扩信号的接收技术不适用于CD3S系统[6-7],解调CD3S信号也因此成为混沌通信领域研究的难点。

混沌同步是实现混沌通信的前提。1990年,文献[8]证明了混沌同步的可实现性,同年,文献[9]首次提出了一种混沌系统的自同步方法。上述研究主要针对由模拟电路实现的连续混沌系统,而模拟电路常常难以精确复制,限制了连续混沌系统同步方法的应用。离散混沌系统由系统初值与混沌映射方程决定,具有易于计算机产生与复制的优点。2001年,文献[10]首次提出了基于扩展卡尔曼滤波(extended Kalman filter, EKF)的离散混沌同步方法,将混沌同步问题转化为混沌序列的状态估计问题,利用EKF构造响应系统实现混沌同步。此后,EKF[11]、无损卡尔曼滤波(unscented Kalman filter, UKF)[7,12]和粒子滤波(particle filter, PF)[13]等非线性滤波技术被广泛用于解决混沌系统的同步问题。

CD3S信号的解调问题与混沌同步问题具有一定的相似性,非线性滤波技术也被广泛用于解调CD3S信号[14-17]。文献[14]将信息符号建立为慢变模型,提出了一种基于UKF的CD3S解调方案。文献[15]用切比雪夫多项式卡尔曼滤波代替UKF,在混沌扩频码具有分段线性特性条件下提高了CD3S信号的解调性能。文献[16]考虑了非高斯噪声干扰对CD3S通信的影响,提出了一种基于PF的CD3S解调方案。对于多径信道下CD3S信号的解调,文献[17]提出了一种联合均衡与解调的CD3S信号接收方案。然而,上述研究将信息符号建立为慢变模型,忽略了信息码状态独立性对非线性滤波器性能的影响,使得扩频因子较小时解调性能下降[18]。

解调CD3S信号需要完成混沌码估计与信息码估计,而混沌码估计与信息码估计均需要以彼此的信息为前提。考虑到混沌码估计与信息码估计之间的关联性,本文利用双扩展卡尔曼滤波(dual extended Kalman filter, DEKF)交替估计混沌码与信息码,通过联合估计实现CD3S信号解调。由于信息码状态间相互独立,不满足固定的状态方程,本文改进了信息码估计时的卡尔曼增益计算方法,避免了信息码状态独立对滤波器性能的影响。

1 CD3S系统模型结构

图1给出了高斯白噪声信道下CD3S通信系统的模型。

图1 CD3S通信系统模型Fig.1 Model of the CD3S communication system

在发射机端,对每一比特的信息码bk∈{-1,1},都用混沌序列{xn}中的N个点xn(n=1+(k-1)N,…,kN)进行扩频。其中混沌序列{xn}由混沌动力学系统生成,描述的状态方程为

xn+1=f(xn)n=0,1,2,…

(1)

CD3S信号{sn}的每一个点均为二进制信息码bk与混沌序列xn相乘得到,即

sn=bkxn

(2)

CD3S信号通过高斯白噪声信道传输到接收端。接收信号为

rn=bkxn+vn

(3)

式中,vn～N(0,Rv)为信道噪声。

2 DEKF联合估计解调算法

2.1 EKF算法

对于非线性系统的估计问题描述的状态方程与观测方程为

yk+1=φ[yk,wk,k]

(4)

zk+1=h[yk+1,μk+1,k+1]

(5)

式中,yk为n维状态向量;zk为m维观测向量;wk为系统噪声;μk为观测噪声;wk与μk均为高斯白噪声，相互独立，均值为0,协方差矩阵分别为Q与R。

图2 EKF结构框图Fig.2 Structure of the EKF

图2给出的EKF算法主要由两组方程构成:预测与更新。预测方程利用当前状态与误差协方差得到下一个状态的先验估计,更新方程则利用观测信息得到改进的后验估计。EKF算法具体描述如下[19]。

(1) 预测方程

(6)

预测误差的协方差矩阵为

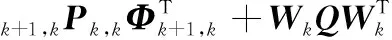
(7)

(2) 更新方程

(8)

卡尔曼增益为

(9)

滤波误差协方差矩阵为

Pk+1,k+1=[I-Kk+1Hk+1]Pk+1,k

(10)

2.2 联合估计解调

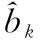
CD3S信号中混沌序列xn的估计问题的描述方程为

(11)

文献[20]认为CD3S系统中混沌序列的状态方程不再固定满足xn=f(xn-1),而是在信息码为-1时满足xn=-f(xn-1),在信息码为+1时满足xn=f(xn-1)。然而由图1不难发现,混沌序列的状态始终满足固定的状态方程,受调制影响的是观测方程。基于式(11),使用EKF算法估计混沌序列状态时,可以将信息码视为系统参数,利用信息码的估计值辅助估计混沌序列。同理,估计信息码时也可以将混沌序列视为系统参数。

在扩频通信系统中bn相对于xn是慢变的,文献[20-21]将信息码的状态方程描述为bn=bn-1,故对信息码bk的估计问题有

(12)

然而信息码的状态间是相互独立的,属于非马尔可夫过程,这不满足卡尔曼滤波及其衍生滤波算法对系统状态的要求,直接由式(12)估计信息码精度较低。此外,由于bn是慢变信号,长期保持同一状态,这会使滤波产生卡尔曼增益退化至0,进一步影响解调性能，下面分析卡尔曼增益退化的影响。

在第2.1节描述的EKF算法中,将式(9)代入式(8)中可得

(13)

由式(13)可知,滤波值由预测值与测量值加权得到,卡尔曼增益利用误差协方差矩阵分配权值。当观测误差方差R=0时,忽略系统线性化误差可得

·

(14)

此时滤波值完全由观测值决定。当卡尔曼增益退化至0时,由式(8)可得

(15)

此时滤波值完全由预测值决定。由于信息码状态相互独立,不能由前一状态预测新的信息码,这就使得直接使用EKF估计信息码解调精度较低。考虑到信息码状态预测值不可信,滤波值中预测值权值可置为0,即

(16)

基于系统的线性化模型有

(17)

(18)

综上所述,基于DEKF联合估计的CD3S解调算法如图3所示。

图3 DEKF联合估计解调算法框图Fig.3 Structure of the DEKF joint estimation demodulation algorithm

算法完整描述如下:

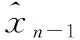
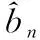
3 仿真分析

仿真使用CD3S通信常用的改进型Logistics混沌序列,其混沌映射方程为xn=1-2(xn-1)2。混沌序列与二进制信息码相乘生成扩频比为50的CD3S信号。

图4给出了信噪比在15 dB时的混沌扩频码同步波形,图5比较了DEKF算法与文献[17]中EKF算法两种算法的混沌码同步性能。由图4与图5可以看出,通过DEKF联合估计,可以实现混沌扩频码的同步,并能减小同步误差。

图4 混沌扩频码同步波形Fig.4 Chaotic spread spectrum code synchronous waveform

图5 混沌扩频码同步均方误差随信噪比变化曲线Fig.5 Change of mean square error with signal-to-noise ratio in thesynchronization of chaotic spread spectrum code

由式(12)直接对信息码进行估计时存在卡尔曼增益退化问题,卡尔曼增益退化曲线如图6所示。卡尔曼增益退化的原因是信息码bk相对于混沌码xn是慢变信号,在对信息序列bn进行估计时,bn在一个扩频周期内始终保持同一状态,就使得卡尔曼增益迅速退化至接近零。当信息序列bn发生变化,由于前一时刻卡尔曼增益值接近零,当前时刻的卡尔曼增益不能有效跟踪误差,影响估计精度,降低解调性能。

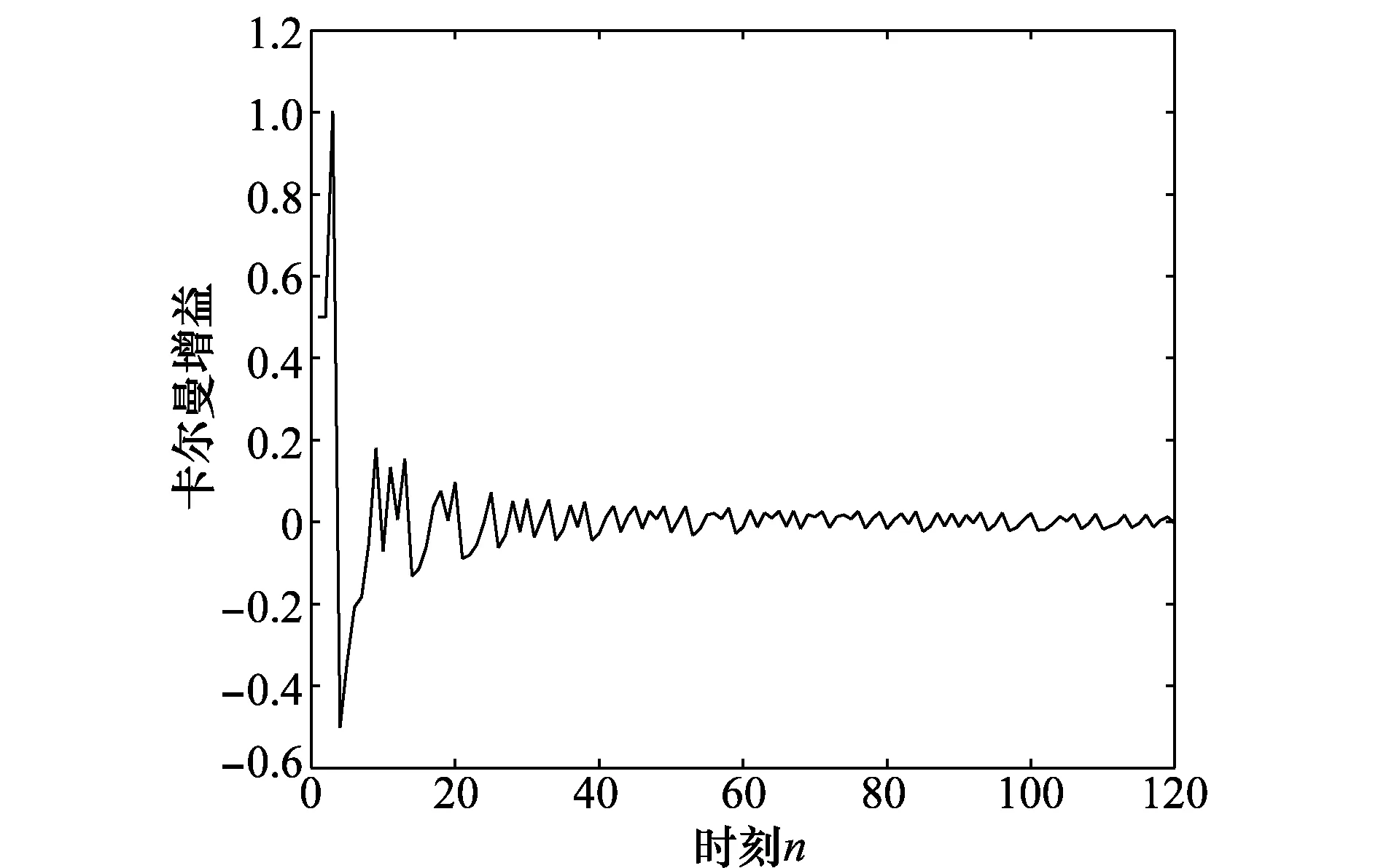
图6 卡尔曼增益退化曲线Fig.6 Degeneracy of Kalman gain

图7 解调过程相关波形Fig.7 Waveform associated with the demodulation

对于解调的性能评价,本文对改进卡尔曼增益DEKF解调算法与文献[17]提出的EKF解调算法进行了仿真比较,得到的误码率随信噪比的变化曲线如图8所示。使用改进卡尔曼增益DEKF解调可以减轻信息码状态独立性对滤波器性能的影响,提高解调性能。

图8 误码率性能对比曲线Fig.8 Comparison of bit error rate performance

4 结 论

本文针对CD3S系统的扩频码同步和信息码解调问题,利用混沌码同步与信息码解调间的关联性,提出了一种基于DEKF联合估计的CD3S信号的解调算法。算法采用DEKF结构,交替进行混沌码估计与信息码估计,通过联合估计可完成混沌扩频码同步,并实现信息码的解调。由于信息码状态间的相互独立,使得利用卡尔曼滤波估计信息码时存在卡尔曼增益退化问题,本文提出的算法也对估计信息码时的卡尔曼增益计算方法进行了改进。仿真结果表明,本文所提出的基于DEKF联合估计的CD3S信号解调算法具有良好的误码性能。