非均匀拓扑网络中的分布式一致性状态估计算法

刘 瑜, 刘 俊, 徐从安, 王 聪, 齐 林, 丁自然

(1. 海军航空大学信息融合研究所, 山东 烟台 264001; 2. 北京航空航天大学电子信息工程学院, 北京 100191)

0 引 言

状态估计是分布式传感器网络应用的核心关键技术[1-4]。为满足诸多应用的实际需求,分布式传感器网络中所有节点或部分节点需要对感兴趣的目标状态实施精确的、一致的估计和预测,从而在每个传感器中都能形成统一清晰的态势信息,有利于在动态变化的监测环境中提高网络任务执行的成功概率及高效性。通过节点协同对目标实施一致性状态估计是分布式传感器网络中一种有效的估计融合方法[5]。该方法基于节点间信息交互式融合的迭代形式,网络中每个传感器都可以利用邻居节点之间的有效信息不断更新本地估计,通过多次迭代循环,可使得每个传感器的本地估计逐渐收敛于全局最优估计,从而实现网络中所有或部分节点对目标状态具有一致的估计[6]。

为探索高效稳定的分布式一致性状态估计方法,国内外已经针对传感器网络目标侦察、搜索、定位、跟踪以及攻击等不同任务背景开展了大量多节点协同估计方法的研究项目[7-9]。2004年,文献[10]首次提出了动态多节点网络系统中构建及解决一致性估计问题的理论框架,受到国际状态估计领域专家的广泛关注,并在传感器网络融合估计、协同决策、编队控制、蜂拥、群移及聚集等多个领域得到了重点研究与应用[11-13];同年,文献[5]基于微型卡尔曼滤波器网络提出了分布式卡尔曼滤波(distributed Kalman filter, DKF)算法,其中每个微型卡尔曼滤波器内嵌了高通高增益一致性协议,能够在本地估计与邻居信息的基础上实现全局状态估计,并消除节点之间的估计差异。然而,DKF仅仅实现了一致性滤波算法的框架设计,无法保证其滤波最优性,可能导致较大的估计误差;2005年,文献[6]研究了DKF离散形式的最优性,设计并实现了DKF的具体算法,并分解为2个动态一致性子问题:加权测量和逆协方差矩阵的计算。其主要思想是利用低通和带通滤波器的分布式算法对数据进行一致性融合,从而达到降低通信代价和抑制噪声的目的。在此基础上,文献[6]提出了经典的卡尔曼一致性滤波(Kalman consensus filter, KCF)算法,其核心步骤是通过相邻节点的信息交互与融合,对邻居传感器之间的状态估计值进行一致化处理,从而获取到关于目标真实状态的最优估计值。但是,KCF的运行条件是网络对目标具有全观测性。2009年,文献[7]通过线性代数、李雅普诺夫和频域分析等方法系统地研究了分布式一致性状态估计问题,分析了一致性滤波器的收敛性、噪声迭代衰减特性和信号快速跟踪能力,研究了最小均方估计误差意义下的KCF算法,阐述了传感器数量和融合能力之间的关系。此外,为解决KCF中协方差更新不适于分布式计算的问题,提出了一种次优KCF算法,并对这种分布式交互滤波算法的稳定性和估计性能进行了有效分析。在此基础上,文献[14]将DKF算法应用于传感器网络群体移动问题,提供了一种用于多智能体网络分布式群移算法设计的理论框架。文献[15]研究了移动无线传感器网络中基于事件驱动机制的分布式滤波算法,其中核心估计技术是卡尔曼一致性滤波器。文献[16]研究了网络拓扑切换下的分布式估计问题,降低了算法所需的通信开销,但估计误差较大,且很难根据收敛条件选取算法中的参数。文献[17]将动态一致性策略用到信息形式的采样型卡尔曼滤波器(sigma-point Kalman filter, SPKF),提出了分布式SPKF(distributed SPKF,DSPKF)算法,其中每个节点利用本地和邻居信息估计全局平均信息贡献值,而不是利用网络中全部的传感器量测信息。然而,SPKF并未考虑节点观测受限的情况。文献[18]针对二进制传感器网络提出了一种分布式动态滤波算法,能够均衡目标状态估计精度与网络开销。2010年,文献[19]通过在DKF算法的状态更新之后增加一个扩散更新步骤,提出了一种分布式的diffKF算法,其中扩散更新的加入能够在一定程度上改善分布式卡尔曼滤波算法的估计性能。2011年,文献[20]针对H∞指标约束问题设计了一种分布式鲁棒滤波算法,以线性矩阵不等式的形式给出了该算法收敛的充分条件;2012年,文献[21]采用信息矩阵加权的方法提出了广义的卡尔曼一致性滤波(generalized Kalman consensus filter, GKCF)算法,提高了分布式估计精度。2013年,文献[22]考虑视频传感器网络中存在盲节点的情况,研究了信息加权一致性滤波算法,获得了逼近集中式估计方法的估计结果,但是该算法仅适用于小型传感器网络;文献[23]研究了异构传感器网络中的无偏及最优一致性滤波问题,提出了基于序贯设计的方法,用于处理两种不同传感器之间的一致性融合,但是该方法并未解决网络盲节点问题。2014年,文献[24]针对非线性系统中的一致性状态估计问题,提出了基于平方根容积卡尔曼的信息滤波器,实现了估计精度的显著提升。2015年,文献[25]介绍了一种分布式稳态滤波器,其结构包括来自相邻节点的测量更新项和关于状态估计的一致项,将滤波器增益的计算转化为凸优化问题。2016年,文献[26]提出了一种分散动态状态估计的递推信息一致滤波器,但是未考虑通信网络的拓扑结构;文献[27]提出了一种基于加权平均一致性的不敏卡尔曼滤波算法,并验证了估计误差下界;2017年,文献[28]研究了未知测量噪声统计的非线性状态估计问题,提出了一种变分贝叶斯一致性容积滤波方法;文献[29]开发了一种适合密集部署的网络信道模型,并引入了一类新的分布式加权一致性策略,可实现本地观测的分布式学习来实现网络定位。由于分布式无线传感器网络通常采用随机部署方式,其网络结构一般具有非均匀拓扑特性,甚至呈现局部小型网络、多簇网络等结构。因此,网络中不同节点间的通信链接在一致性估计融合中应该具有不同的重要性,而KCF等传统估计算法及其后续的改进算法在一致性信息迭代时将所有节点通信链接的对应权值视为相等,容易导致一致性收敛速度受到网络中某些“桥梁”链接的负面影响。针对上述问题,本文研究了网络资源受限条件下的节点协同一致性状态估计框架,分析了目标状态一致性的主要流程,并根据节点通信链接的重要性设计了基于网络动态拓扑信息的自适应权值分配策略,并基于此权值分配策略,提出了基于自适应加权的卡尔曼一致性滤波算法(adaptive weighted Kalman consensus filter, AW-KCF)。仿真结果显示,AW-KCF在节点稀疏等网络非均匀拓扑情况下相对于KCF具有较为优越的估计性能。

1 分布式传感器网络一致性状态估计功能模型

对于大型分布式传感器网络中的目标状态估计应用,由于网络资源受限,节点的传感区域和通信范围通常是有限覆盖的,因此单个时刻并不是每个节点都能实时观测到穿越监测区域的目标,仅在特定的时间段内少数节点具有对目标的实时量测。此时,若要实现整个网络中所有或大部分节点对目标的一致性状态估计,则需要节点间执行足够多次的信息转发与迭代,毫无疑问,这期间将耗费大量网络通信与计算资源[30],且目标状态的单个滤波周期与信息迭代次数相关,将直接影响到态势生成速度。

实际上,网络经过随机或人为部署后,自组织的通信方式能够保证网络中所有的连通节点都具有向上汇报监测信息的路由通道[31]。因此,在资源受限的大型传感器网络中,并不都是随时要求全网实现一致估计,只需网络中部分节点形成对目标的统一估计便能满足实际应用需求。此时,可以在单个估计时刻合理选择一部分节点构成局部网络(不妨称为一致性节点集),通过集内节点间合理高效的信息交互与融合,实现局部网络对目标的分布式一致性状态估计,以便于实施有效的目标跟踪与预测。此外,随着目标在监测区域内不断移动,实施状态估计的一致性节点集是动态变化的,因而可以在节点间的信息交互的过程中实时更新集内成员信息。

对于一致性状态估计流程,由于传统两级功能模型无法清晰地描述资源受限时分布式传感器网络中的一致性状态估计问题,本文根据估计的功能层次,从估计过程出发,把一致性状态估计分为4级,依次是模型初始化层、信息处理层、一致性融合层和状态估计层,如图1所示。这是一种广义的一致性状态估计功能分级法,描述了状态估计过程中各步骤之间的相互作用关系,是传统两层分级法的扩展形式,提供了一种通用的信息处理及流通模式,有利于一致性状态估计技术的研究。以下分别描述各层的主要功能和内容。

图1 分布式传感器网络一致性状态估计功能模型Fig.1 Functional model of consensus state estimation fordistributed sensor network

(1) 第1级是模型初始化层。基于概率模型对现实环境进行抽象用以描述实际系统,并且根据应用需求建立一致性节点集。其中,对实际系统的描述包括实际状态、量测、状态转移和量测模型的精确表述;一致性节点集是指在滤波过程中参与信息交互与融合并最终实现对目标状态一致估计的传感器节点组合。

(2) 第2级是信息处理层。根据具体一致性算法,基于估计模型及目标量测等本地信息,网络中各节点计算本地一致性参数,为节点间的信息互传与融合做好准备。

(3) 第3级是一致性融合层。一致性节点集内的传感器节点广播本地一致性参数,并接收邻居节点发送的参数,然后基于设定的估计融合规则,利用邻居传送的信息对本地一致性参数进行更新。此过程迭代足够多次,最终实现一致性节点集内的所有传感器节点具有相同的一致性参数。

(4) 第4级是状态估计层。网络中各传感器基于信息互传及迭代处理后得到的一致性参数,对目标状态进行全局估计,并基于状态转移模型得到目标状态的预测。至此,一致性节点集内的所有节点均获得了相同的目标状态估计和预测。

为便于描述,表1给出了分布式传感器网络一致性状态估计的具体实施流程。需要说明的是,本文所设计的一致性状态估计算法均将采用上述4级功能模型中的信息处理与流通方式,且其研究重点在于节点对目标状态的一致性融合规则。

表1 节点协同一致性状态估计流程

从表1可见,在模型初始化层,当前观测节点将前一时刻的目标状态广播至网络中,并引入一跳邻居盲节点参与一致性状态估计过程中的信息交互与融合,能够保证观测节点及其一跳邻居盲节点对目标状态的一致估计。如此设计,便于下一时刻传感器量测与已有目标航迹的数据互联,能够有效防止因目标快速机动而导致估计失败甚至目标丢失的情况,避免新航迹层出不穷、航迹不明等现象。此外,由表1所述可以看出,通过节点间的信息迭代交互与融合,各传感器不断获取周围邻居节点的估计信息并基于合理有效的融合规则来更新本地估计,从而逐渐收敛于相对一致的全局估计。其中,信息交互的形式、内容以及融合规则,将直接影响到一致性估计的精度和速度。

2 AW-KCF算法

2.1 问题描述

传感器网络中节点之间的通信连接可由无向图G=(S,E)来表示,其中S={S1,S2,…,SNS} 包含了图中所有的顶点,表示网络中的通信节点,其中NS为节点数量,而集合E包含图中所有的边,表示网络中不同节点建立起来的可行通信链接。此外,以Sk表示k时刻网络中的节点集合,以Ni表示所有与Si有直接通信连接的节点的集合,即Ni中的每个节点都与Si构成图中的某一条边,都是Si的邻居节点。不妨假设单个节点Si仅具有一个传感器,在k时刻观测到目标,则Si称为观测节点,其线性高斯系统中的状态转移及量测模型可表示为

xk+1=Φxk+wk,k=0,1,2,…

(1)

zi=Hixk+vi,k=0,1,2,…

(2)

式中,xk∈Rnx、zi,k∈Rnzi分别表示k时刻的目标状态及传感器Si的量测,其中nx为状态维度,nzi为传感器Si的量测维度;Φ∈Rnx×nx为状态转移矩阵,过程噪声wk∈Rnx为零均值的高斯白噪声,即wk～N(0,Q);Hi∈Rnzi×nx为传感器Si的可时变观测矩阵,vi∈Rnzi为零均值的高斯白噪声,即vi,k～N(0,Ri)。

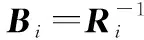
一致性状态估计过程及其主要任务为:基于目标量测zk[z0,z1,…,zk],以分布式的方式解算被估目标的全局状态信息,并以条件概率密度函数的形式表示估计结果,通过邻居节点之间的信息迭代处理与融合实现网络中所有或部分传感器对目标的一致估计。

2.2 KCF算法

不失一般性,本文采用经典的KCF算法[6]作为对比分析文献。根据文献[6]所述,作用于变量a的一致性单次迭代过程可以表示为

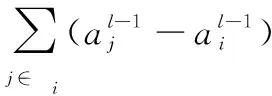
(3)

式中,l=1,2,…,L为迭代次数;ζ为一致性速率因子。由式(3)可知,网络中每个传感器都能够综合相邻节点的状态信息,通过这种局部邻居之间的信息传递与融合机制,所有传感器对目标的最终状态估计都将逐渐趋于一致[6]。

基于上述一致性信息迭代与融合过程,文献[7]提出了经典的KCF算法,首先在每个观测传感器内执行卡尔曼最优滤波步骤,然后通过邻近节点之间信息交互与融合实现状态估计的一致性。该文对KCF算法进行了详尽的算法推导及最优滤波稳定性分析,在此不再赘述。表2描述了KCF算法的具体步骤。

由表2中的公式推导可见,KCF算法采用了平均一致性方法综合了邻居节点之间的状态估计(见表2中步骤6),并且所有节点的状态估计在求和式中具有固定相同的一致性速率因子ζ。其中,ζ的取值空间通常为(0,1/Δmax),Δmax为网络中最大的节点度[7]。

表2 KCF算法步骤

2.3 基于动态拓扑的自适应一致性速率因子

分布式传感器网络一般具有非均匀拓扑特性,实际上,节点之间的可行通信链接取决于是否在彼此的信号传输距离之内。于是,随机部署的分布式传感器网络中,相邻节点可能拥有多个相同邻居节点,也很可能并无相同邻居节点,此时易于构成相互连通的多个局部小型网络,即多簇结构[32],如图2所示。

图2 多簇结构的分布式传感器网络Fig.2 Distributed sensor network with multi-clusters

上述案例说明,在多簇结构等不均匀拓扑的分布式传感器网络中,节点之间的通信链接对信息的流通速度具有重要的影响力。因此,为加速网络节点对目标状态的一致性估计,需要根据网络中节点间的拓扑特性来设计合理的一致性速率因子,即不同节点的信息在一致性融合过程中应具有不同的速率因子。从直观上分析,一种加速一致性收敛的方法就是根据节点间通信链接的重要性来设计该链接对应的速率因子,也就是说,越为重要的链接应该赋予更高的权值,尤其是类似于图2中连接了2个局部网络的“桥梁”链接。

(4)

综上,为提高不均匀拓扑网络中节点对目标状态的一致性收敛速度,基于Jaccard相似度,提出了基于动态拓扑的一致性速率因子分配(adaptive assignment algorithm for consensus-rate factor, ACF)算法,其具体设计过程如表3所示。节点首先广播自身邻居信息,然后根据自身与邻居在拓扑结构方面的相似性来计算不同通信链接对应的一致性速率因子,具体总结如下。

表3 ACF具体步骤

2.4 AW-KCF算法描述

对于典型一致性状态估计方法KCF,其假定的运行条件是网络中所有传感器均能实时观测到目标,且需要预知固定且相同的一致性速率因子,这在节点观测受限的大型分布式传感器网络中难以获取满意的估计性能。在此,本文在KCF的基础上,引入第2.3节提出的动态自适应一致性速率因子计算方法ACF,将KCF扩展至分布式传感器网络一致性状态估计框架,提出了AW-KCF算法(ACF也可用于其他类似的一致性估计方法),其具体估计过程如表4所示。

表4 AW-KCF算法步骤

续表4

3 验证与分析

为验证本文所提自适应权值分配策略ACF对一致性估计的有效性,以下构建了随机拓扑的分布式传感器网络对所提方法AW-KCF与典型方法KCF进行仿真比较。需要说明的是,不失一般性,本文的仿真实验中隐去了相关变量的距离单位,可根据具体应用参考本文中的仿真环境设置及仿真结果。本文仿真中,将NS=50个节点随机部署在100×100的方形区域,各节点具有同等的通信半径Rc。若任何两个节点之间的距离小于Rc,则认为这两点是可以进行正常通信的。图3显示了不同通信半径下的随机拓扑网络。

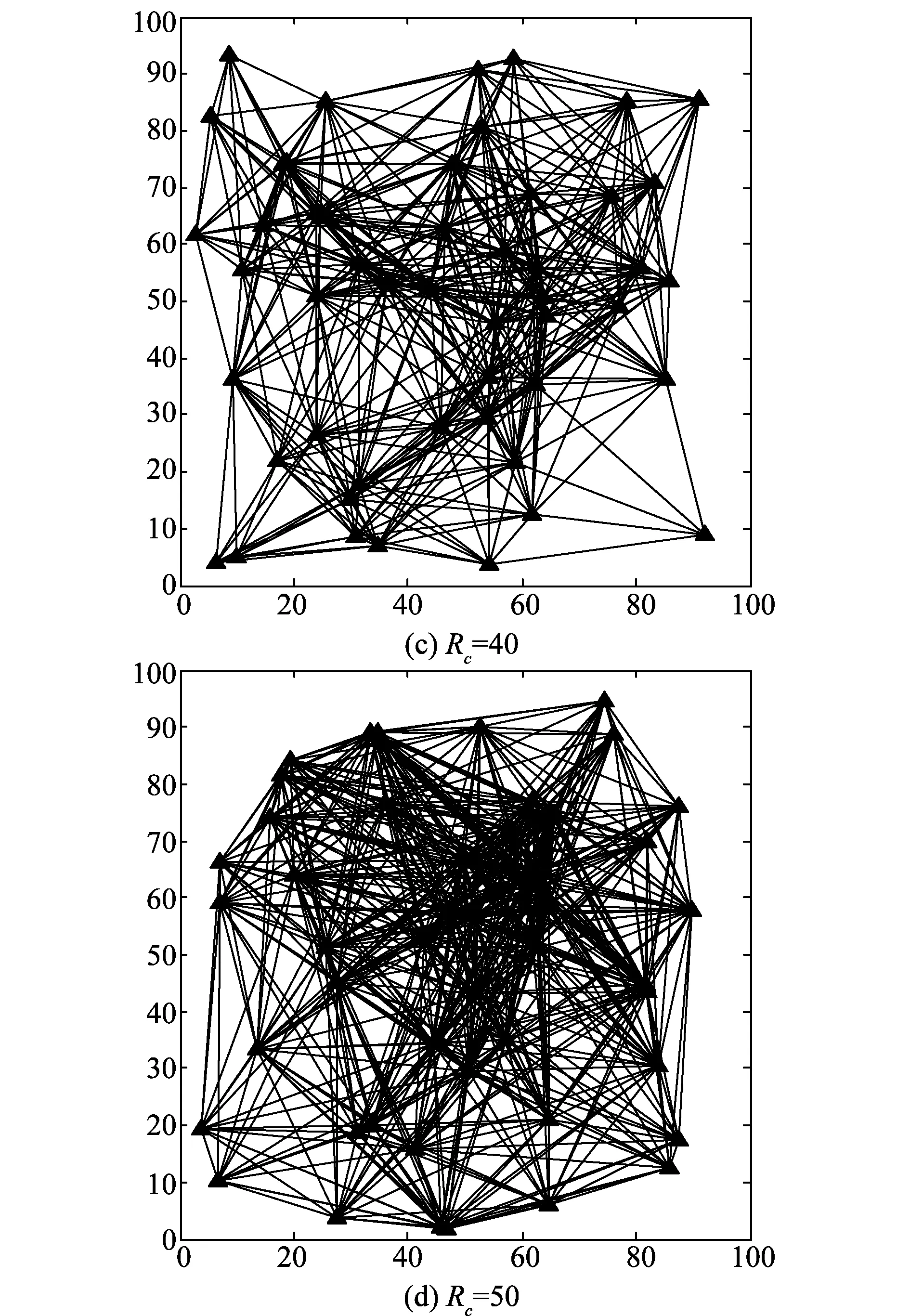
图3 不同通信半径下的随机拓扑网络(50个节点)Fig.3 Random geometric graphs with different communicationradius (50 nodes)

由图3可见,当通信半径较小时(Rc=20),网络展现出多簇结构,簇间的通信链接对一致性收敛速度影响较大。随着通信半径的增大,网络中的可行通信链接逐渐增多,最终将实现全连通网络。目标状态转移及量测模型如式(1)与式(2)所示,且有

此外,KCF采用AW-KCF中同样的一致性迭代方式,只是KCF中设置一致性速率因子为固定值ζ=0.65/Δmax,其中Δmax为网络中的最大节点度,而AW-KCF采用动态自适应的一致性速率因子。

为考察不同网络拓扑情况下一致性速率因子对收敛速度的影响,假定网络中的节点均能观测到监测区域中的目标,即NC=NS,均值估计误差表示为

(5)

图4 均值估计误差随一致性迭代次数变化情况Fig.4 Performance comparison of different number of consensus

由图4可见,当节点的通信半径较小时,AW-KCF的一致性收敛速度明显快于KCF,并且在一致性迭代次数较少时取得优于KCF的估计精度。这是因为,较小的通信半径造成网络连通较为稀疏,容易形成多簇结构,而对于一致性收敛,簇间的链接相对于其他节点间链接来说更为重要。此时,若将节点间所有链接对应的速率因子视为相等,一致性收敛速度势必受到网络中部分“桥梁”链接的负面影响。从方法设计及仿真结果来看,AW-KCF通过对网络拓扑结构的分析,根据节点间通信链接的重要性设计了动态自适应的速率因子,能够较好地分配速率权值,在收敛速度方面取得了改进效果。例如,图4(a)中,KCF执行9次一致性迭代才趋于收敛,而AW-KCF仅需5次。随着节点通信半径的增大,网络中的通信链接不断增多,单次一致性迭代所能融合的传感器信息也在逐渐增加。因此,KCF与AW-KCF的均值估计误差曲线逐渐趋于一致,如图4(b)～图4(d)所示。上述仿真结果说明,在稀疏连通的网络中,有必要根据一致性节点集内成员构成的拓扑结构来设计动态变化的速率因子,从而能够加速网络一致性收敛。

4 结 论

针对传感器网络中节点对目标的分布式一致性估计问题,研究了节点协同一致性状态估计框架,根据状态估计功能的层次性和信息处理及流通方式,提出了4级功能模型,揭示了一致性状态估计技术中的数据处理及融合过程;其次,考虑到网络不均匀拓扑时一致性收敛较慢的情况,根据节点间通信链接的重要性设计了基于网络局部动态拓扑信息的自适应权值分配策略,并以经典的KCF方法为例,基于动态自适应的一致性速率因子提出了相应的改进算法,在非均匀拓扑的稀疏网络中显著提高了一致性收敛速度。