面向应急需求的成像卫星单任务综合规划
2018-09-27杨正磊钟文冬任登高谢夏洁
杨正磊, 钟文冬, 席 涛, 任 猛, 任登高, 谢夏洁
(1. 宇航动力学国家重点实验室, 陕西 西安 710043; 2. 西安卫星测控中心, 陕西 西安 710043)
0 引 言
我国已逐渐建立起了自己的天基对地观测系统,可获得可见光、多光谱、合成孔径雷达(synthetic aperture radar,SAR)及红外等多种类型的图像,极大地提高了天基态势感知能力。通过成像卫星进行对地观测,已成为获取情报信息的重要技术手段。早期,由于卫星数量及其载荷能力有限,用户需求相对较少,综合规划的问题并不突出,随着卫星种类、数量及用户需求逐渐增加,特别在应急条件下,应用需求具有突发性和时效性要求高的特点,如何就现有成像卫星资源进行综合规划,进一步缩短响应时间,已成为当前成像卫星系统运用亟待解决的问题。
目前,类似问题的研究主要以成像卫星任务规划为背景,大致可分为单星成像调度问题和多星成像调度问题两类[1-6],建立的模型包括混合整数规划模型、0-1规划模型、约束满足问题模型、动态约束满足问题模型、Petri网模型、基于图论的模型等,模型的求解包括贪婪算法、混合整数规划算法、启发式算法及智能搜索算法等,模型大多选取以满足任务需求综合最优或多个目标为优化目标。针对应急条件下任务规划问题,相关文献[7-8]研究了多星协同调度问题,并通过粒子群算法对建立的模型进行求解等。然而,已有研究问题模型的建立大多以平时任务需求为背景,或只考虑了卫星或综合卫星[9]、数传资源的规划。事实上,一方面,中继卫星[10]系统的逐步完善,对于低轨卫星的覆盖率理论上能达到100%,可大大缩短响应时间,但目前一些成像卫星并不具备中继测控及数传能力,只依靠中继卫星进行任务响应则需求不能面向所有在轨卫星;另一方面,目前任务响应时间的制约因素主要源于对系统间资源以“申请”为主的使用方式,但随着测控运控一体化的推进与发展,系统间资源逐渐具备统一调度的能力。综合以上两方面原因,应急条件下,考虑包括测控资源在内的各类星地资源,尽可能地缩短任务需求响应时间,进行任务综合规划研究是有必要也有意义的。因此,本文的研究拟建立在各类星地资源均可进行统一规划的前提下,以应急条件下成像卫星任务规划为背景,研究单个任务需求条件下综合规划问题,首先给出规划要素及涉及约束的形式化描述,建立应急条件下成像卫星单任务规划模型,在此基础上,基于深度优先搜索的思想进行模型求解,最后通过算例分析进行模型及算法的有效性验证。
1 问题分析
1.1 成像卫星任务响应过程分析
依据成像类型的不同,成像卫星可分为可见光、红外、多光谱及SAR成像卫星等,典型的任务响应过程如图1所示,具体描述如下:
(1) 用户根据需要提出任务需求;
(2) 运控系统根据用户提出的任务需求,制定卫星工作和数据接收计划,分别发往测控和运控系统;
(3) 测控系统根据卫星工作计划对卫星进行测控,以建立卫星工作状态,卫星适时进行成像;
(4) 运控系统根据数据接收计划,分配数据接收站,并将接收到的数据发往应用系统;
(5) 应用系统对数据进行处理后发往用户。
根据图1的描述,成像卫星的任务响应过程基本上遵从接收任务需求-卫星测控(建立工作状态)-成像-数据接收等几个过程。涉及的要素包括用户需求、卫星、测控资源、数传资源等,如何在应急条件下有效地对任务响应过程中各个要素进行协同,实现任务快速响应,是本文进行的任务综合规划主要解决的问题。
1.2 任务响应过程约束分析
成像卫星工作过程看似是顺序的,简单的要素的分配,然而,在实际应用的过程中,面临诸多约束,建立问题模型之前,须对其中的约束予以分析,体现在以下几个方面:
(1)任务需求与卫星之间存在成像需求与卫星载荷类型的匹配性、分辨率需求及成像条件约束;
(2)卫星与用于测控的测控资源之间存在测控体制及可见性约束;
(3)卫星与用于数据接收的数传资源之间存在数传体制及可见性约束;
(4)任务响应过程存在接收到任务需求-卫星状态建立-成像-数据接收的时序性约束。
2 应急条件下单任务综合规划模型
本节在对其中涉及的要素、约束进行形式化描述的基础上,建立相应的问题模型。
2.1 要素的形式化描述
应急条件下卫星综合任务规划以任务需求为输入,涉及卫星、测控及数传资源的分配,最后给出规划结果,本节对其进行形式化描述。首先,定义几个集合。卫星的成像类型集合描述为ScoC={可见光,红外,多光谱,雷达};测控资源测控体制集合描述为CC={S,C,Ka,X,STL},分别表示{S频段,C频段,Ka频段,X频段,中继测控};数传资源数传体制集合描述为DC={S,C,Ka,X,KaTL},分别表示{S频段,C频段,Ka频段,X频段,中继数传}。在此基础上,将任务规划涉及的要素作如下形式化描述。
(1) 成像任务需求描述为一个六元组TSco={TID,ts,TPos,TType,TRes,T_t},其中:
TID:任务编号;
ts:任务需求时刻;
TPos:TPos=(long,Lat.),表示成像目标位置;
TType:TType∈ScoC,表示任务需求成像类型;
TRes:分辨率要求,单位为m;
T_t:T_t=[α,β],观测需求的时间范围(地方时),其中,α和β分别表示观测需求允许的开始和结束时间,若α和β为0,则表示不对开始或结束的观测时间作要求。
(2)卫星资源及其特征描述为一个六元组SScoi={SName,SOrbit,STandR,STCGtype,SD typeB,SSA},其中:
SName:卫星名称;
SOrbit:SOrbit=(a,e,i,Ω,ω,M),表示卫星轨道六根数;
STandR:成像类型及分辨率,STandR={(SType1,SRes1),…,(STypei,SResi),…},其中,STypei∈ScoC,SResi表示分辨率,单位为m;
STCtype:可测控体制,STCtype⊂CC;
SD typeB:可数传体制及带宽,SD typeB={(SD type1,SDbw1),…,(SD typei,SDbwi),…},其中,SD typei∈DC,为可数传体制,SDbw表示数传带宽,单位为Mbps;
SSA:最大侧摆角度(°),若为0,则表示无侧摆能力。
包含m个卫星资源的几何描述S={S1,S2,…,Sm}。
(3) 测控资源包括地基测控资源和天基测控资源,测控资源描述为C={CID,CGpos/CSorbit,Csys},其中:
CID:测控资源ID;
CGpos:地基测控资源位置,CGpos=(long,Lat.,alt.),分别表示经度、纬度、海拔;
CSorbit:天基测控资源轨道,CSorbit=(a,e,i,Ω,ω,M),为轨道六根数;
Csys:测控资源可测控体制,Csys⊂CC。
包含n个测控资源(地基测控站/中继测控)的测控资源集合,可以描述为C={C1,C2,…,Cn}。
(4) 数传资源同样分为地基数传站和天基数传资源。数传资源描述为D={DID,DGpos/DSorbit,Dsys},其中:
DID:数传资源ID;
DGpos:地基数传资源位置,DGpos=(long,Lat.,alt.),分别表示经度、纬度、海拔;
DSorbit:天基数传资源轨道,DSorbit=(a,e,i,Ω,ω,M);
Dsys:数传资源可接收数传体制及带宽,Dsys={(DD type1,DDbw1),…,(DD typei,DDbwi),…},其中,DD typei⊂DC,数传资源可数传体制,DDbwi表示数传带宽,单位为Mbps;
包含j个数传资源(地基数传站/中继数传),数传资源集合可以描述为D={D1,D2,…,Dj}。
(5) 规划结果描述了针对应急条件下卫星任务需求,经规划为其分配的卫星资源、测控及数传资源。对于给定的应用任务需求Ti,其规划结果可以描述为R={T,SR,CR,DR},其中:
T:任务需求;
SR:完成任务所需的卫星资源,SR∈S;
CR:卫星资源建立工作状态所需的测控资源规划结果,描述为CR=(CRID,Carc),分别表示测控资源及其测控弧段,其中CRID∈C.CID,Carc=[Carcα,Carcβ]∈fc(SR.SOrbit,CR),fC表示卫星与测控资源的可见约束。
DR:接收卫星资源所需的数传资源规划结果,描述为DR=(DRID,Darc),分别表示数传资源及其数传弧段,其中,DRID∈D.DID,Darc=[Darcα,Darcβ]∈fD(SR.SOrbit,DR),fD表示卫星与数传资源的可见约束。
2.2 问题假设
模型的建立及进行算法求解时作如下假设:
(1) 任务需求为点目标成像任务;
(2) 接收到成像任务需求后,在一个测控弧段内能对卫星完成测控并建立工作状态;
(3) 数据能在一个数传接收弧段内完成,且数据接收完成时刻定义为弧段结束时刻;
(4) 考虑数据实传的情况,数据接收时刻不早于成像开始时刻。
2.3 单任务综合规划模型
基于上述对规划要素的形式化描述、约束条件分析及问题的假设,建立应急条件下成像卫星单任务综合规划问题模型,表示如下:
f(R)=minte,te=R.DR.Darc.Darcβ
(1)
s.t.
∃STandR.STypei∈SType,STandR.STypei=T.TType
(2)
S.STandR.SRes≤T.TRes
(3)
fW(SR.SOrbit,T.TPos,SR.SSA)≠∅且fW∈T.T_t
(4)
∃STCtypei∈STCtype,STCtypei∈CR.Csys
(5)
fc(SR.SOrbit,CR)≠∅
(6)
∃SD typei∈SD type,SD typei∈DR.Dsys且SDbwi≤DR.DD typei
(7)
fD(SR.SOrbit,DR)≠∅
(8)
T.ts (9) CR.Carc.Carcβ≤Warc.Warcα (10) Warc.Warcα≤DR.Darc.Darcα (11) 式中,Warc=[Warcα,Warcβ],且Warc∈fW(SR.SOrbit,T.TPos,SR.SSA),fW表示卫星与成像目标点位可见性约束。应急任务需求条件下,希望在提出任务需求后能尽快获得成像数据,若提出任务需求的时刻为ts,任务需求响应结束时刻te,对于单个成像任务而言,任务需求响应结束时刻即为数据接收完毕的时刻,即te=DR.Darc.Darcβ,因此,提出如式(1)所示的优化目标函数,式(2)~式(11)分别表示对第1.2节中所述约束的数学描述。 事实上,本文建立的单任务综合规划模型中涉及大量的数据计算,同时也是进行模型求解的基础。 首先,卫星资源与测控资源、数传资源之间存在可见性约束分析计算,即模型中所述的fC、fD,测控、数传等地面资源的可见约束模型如图2和式(12)所示[5],一般,仰角E>5°即视为可见。 图2 地面站与卫星可见约束示意图Fig.2 Visible restriction between station and satellite (12) 式中,β=L′,rS=rE+R。 此外,模型中还涉及卫星与成像目标点位的可见性约束fW计算,与卫星轨道、最大侧摆角度等要素有关,如图3所示,其数据计算可通过STK(SIM tool kit)进行。 图3 卫星成像约束示意图Fig.3 Restriction of satellite imaging 在上述数据计算的基础上,进行模型求解算法设计。 通过对成像卫星工作过程及其要素间存在约束的分析,假设卫星、测控及数传资源的数量分别为m,n,l,则规划结果将在m×n×l的搜索空间内产生,随着卫星、测控及数传资源数量及种类的增多,复杂性也随之增加[11],与此同时,要素之间还存在式(2)~式(11)描述的约束。对于单个任务需求而言,整个搜索空间可以看成是以任务需求为根节点的树形网状结构[12],按照模型假设,规划结果必须包含卫星、测控及数传资源等要素,那么模型的求解过程即是在整个搜索空间内寻找一条路径,使得模型提出的优化目标函数值最小[13],如图4所示。 图4 任务规划搜索空间示意图Fig.4 Search space of mission schedule 若卫星集合S={S1,S2,…,Sm},测控资源集合C={C1,C2,…,Cn},数传资源集合D={D1,D2,…,Dl},模型解的搜索空间与图相似又不同于图,同时节点之间又存在约束[14],是一个涉及天地资源协调的约束满足[15-16]问题,本文借鉴深度优先搜索[17]的思想构建模型的求解算法,在搜索过程中处理要素之间的约束,描述如下: 输入成像任务需求T。 输出R={T,SR,CR,DR}。 步骤1初始化参数i=1,j=1,k=1,Carc=∅,Darc=∅,tE=∞,R=∅,flag=0; 步骤2对于Si∈S,计算Warc=fW(Si.SOrbit,T.TPos,Si.SSA),若同时满足约束(2)~约束(4),则转入步骤3,否则转入步骤6; 步骤3对于∀Cj∈C,计算Ctemp=fc(Si.SOrbit,Cj),若同时满足约束(5)和约束(6),则在满足约束(9)、约束(10)的前提下,计算Carc=minCtemp; 步骤4对于∀Dk∈D,计算Dtemp=fd(Si.SOrbit,Dk),若同时满足约束(7)和约束(8),则在满足约束(11)的前提下,计算Darc=minDtemp,得出Darc.Darcα; 步骤5若Darc.Darcα 步骤6i=i+1,若i>m,退出; 步骤7转入步骤2。 计算完成后,若flag=1,即可得到规划结果R={T,SR,CR,DR},即为针对任务需求T,运用本文提出的算法计算得到的任务规划结果,理论上,只要计算时间区间足够长,总能得到满足任务需求的规划结果。 为了验证模型及算法的正确性及可行性,选择10颗不同类型的卫星组成的成像卫星系统,10个测控资源(含天基测控资源)组成的测控系统,6个数传资源(含天基数传资源),卫星、测控及数传资源信息分别如表1~表3所示,基于STK,运用本文建立的模型及算法进行仿真计算验证。其中,天基测控、数传资源与卫星可见计算时,假设扫描角为[50°,80°]。 仿真计算起始时间(UTC)27 Jul 2016 00:00:00,结束时间(UTC)30 Jul 2016 00:00:00,假设由于某应急任务,需要分别对坐标为(157.9°W,21.3°N)和(109°E,34°N)的两个目标进行成像侦察,则不同任务需求条件下的计算结果如表4所示,表中时间为UTC时。 表4为不同任务需求下的规划结果。需求1和需求2比较,成像任务需求相同,但触发时刻及分辨率要求不同,对卫星、测控及数传资源的选择也会不同;需求1、3和需求4、5分别进行比较,成像类型需求不同,对卫星进行约束的同时,进而也会影响测控及数传资源的分配;需求3和需求4比较,成像点位不同,由于卫星过境的时间约束,使得为其分配的数传资源不同。 此外,在原有仿真条件下,对不考虑测控资源在内的卫星-数传资源规划进行了仿真分析,假设运控向测控系统的资源申请所需时间为30 min,仿真规划结果如表5所示,两种模式下响应时间对比如图5所示。不难看出,表5中,对于任务需求3、4,尽管总的响应时间不变,但所需的测控资源有所变化,对于任务需求5,其响应时间则大大增加,并且,随着可用卫星、测控、数传资源数量的增加,这种影响将随之增加。 表1 卫星资源信息 表2 测控资源信息 表3 数传资源信息 表4 不同任务需求条件下的规划结果 表5 不考虑测控资源情况下的规划结果 图5 规划结果响应时间比较Fig.5 Comparison of responsing time with different scheduled mode 通过上述仿真分析,并从分析结果看,可以得出如下结论。 首先,本文建立的面向应急需求的成像卫星单任务综合规划模型有效,能够就给定的单个任务需求情况下,通过对卫星、测控、数传资源的综合规划,能够得出可行且响应时间最短的星地资源分配方案。 其次,本文提出的星地资源综合规划模型,较现有只考虑卫星或卫星-数传资源规划,能够有效降低整个应急任务需求的响应时间。 本文针对成像卫星单任务需求条件下的综合规划问题,考虑卫星、测控及数传资源规划,以任务响应最快为优化目标,建立了应急条件下成像卫星单任务综合规划的约束满足优化模型,并基于深度优先搜索的思想,给出了相应的模型求解算法。仿真分析结果表明,建立的模型有效可用,对于应急条件下成像任务需求,能够规划给出响应时间最短的星地资源分配方案,且与卫星-数传资源联合规划的模式比较,能够有效降低需求响应时间。应急任务需求往往是并发的或者可能涉及区域目标的分解,下一步研究将在此基础上针对多任务需求条件下的综合规划问题展开。3 模型求解
3.1 数据计算
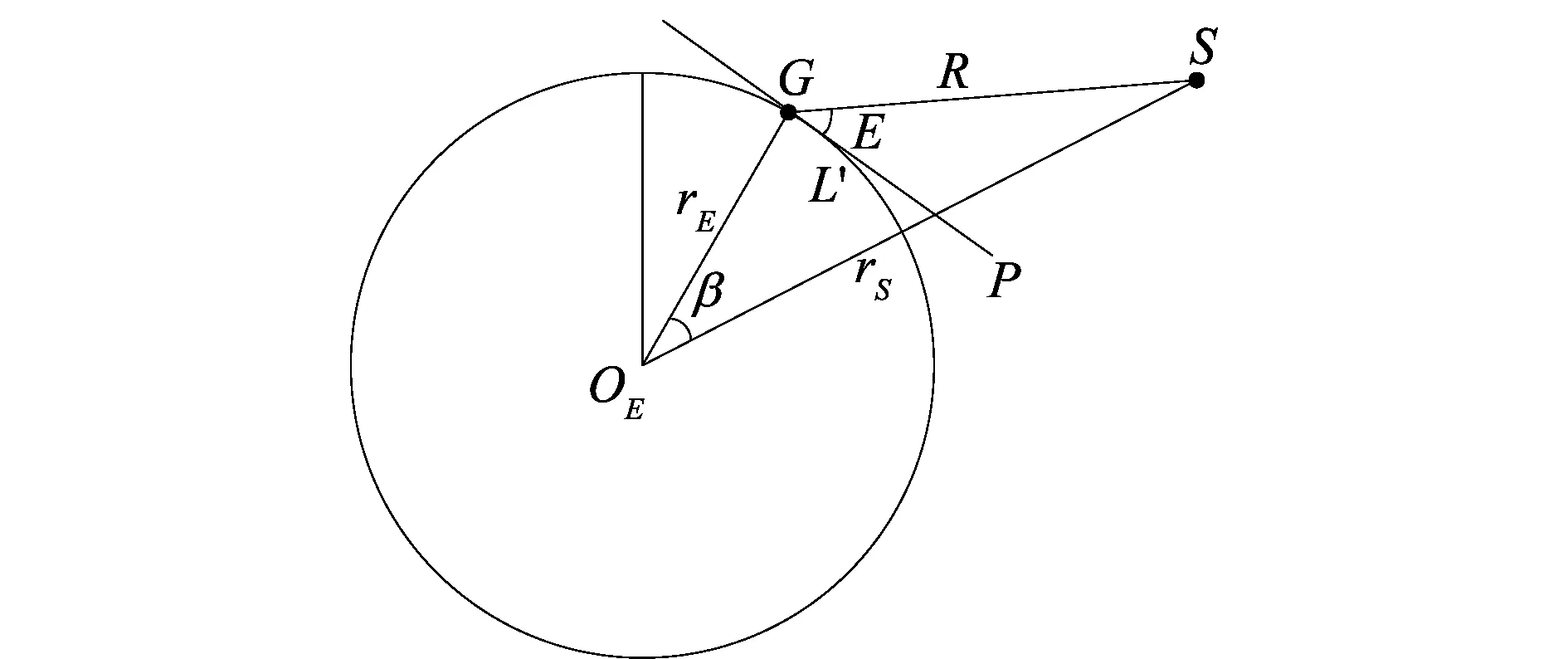
3.2 基于深度优先的模型求解算法
4 仿真验证
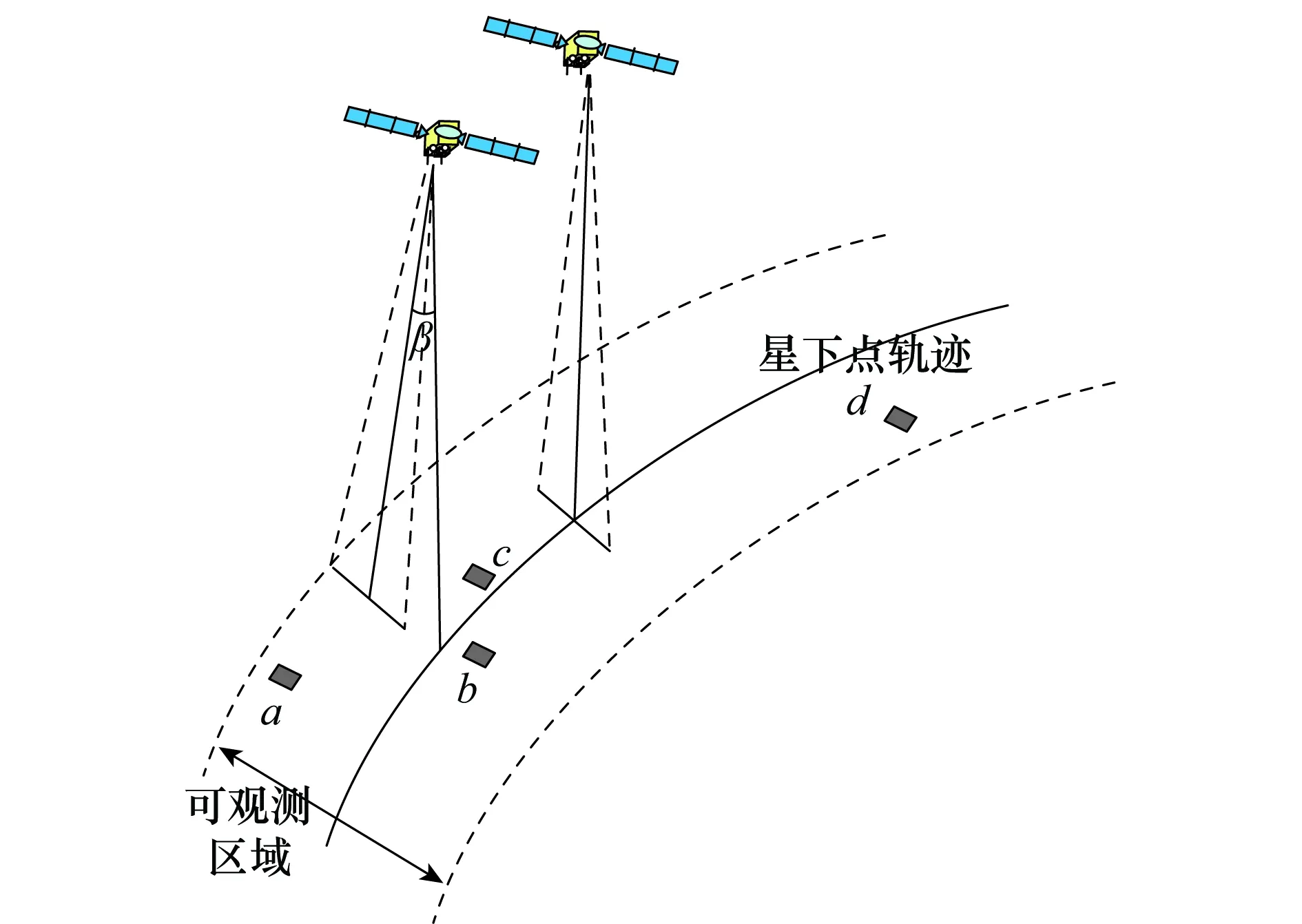
4.1 仿真分析
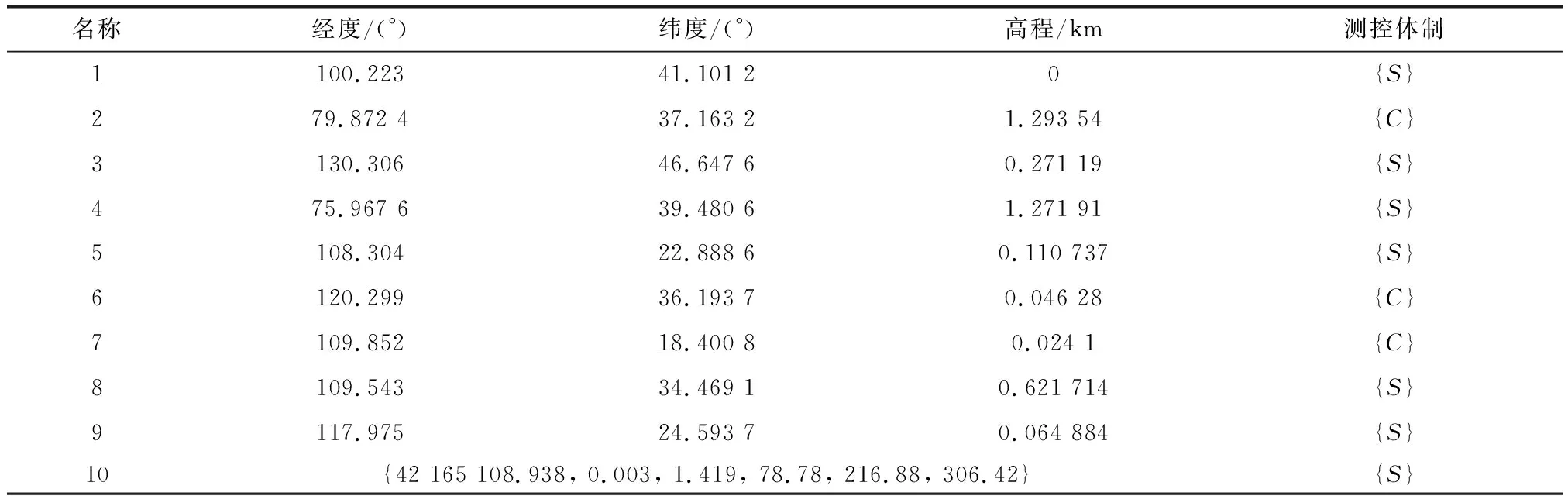
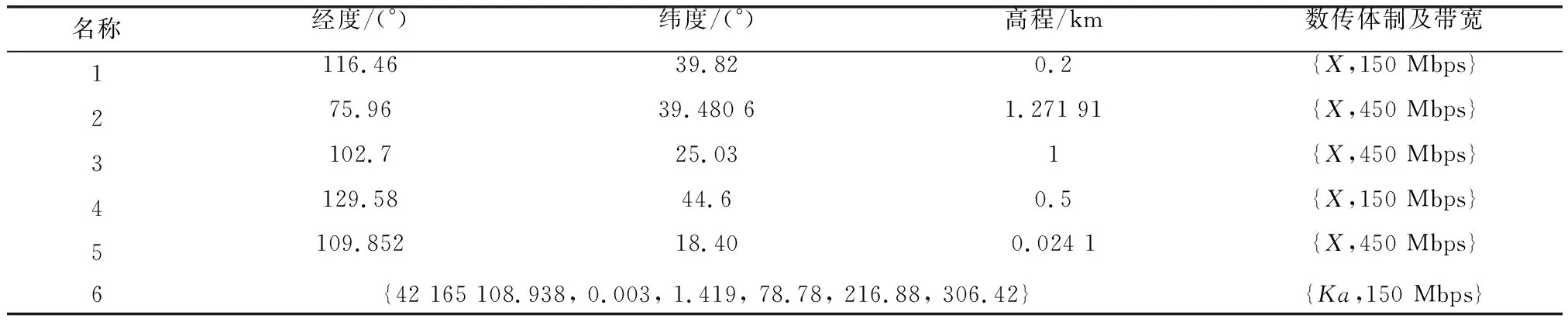



4.2 仿真结论
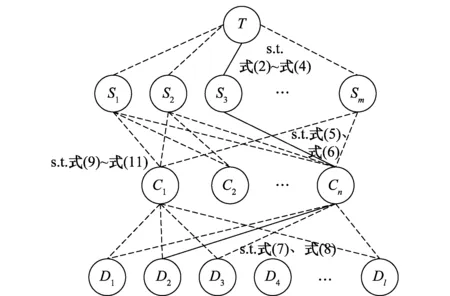
5 结术语
