基于波形特征的外辐射源雷达杂波抑制算法

赵志欣，周新华，朱斯航，洪 升，王玉皞

(南昌大学信息工程学院，江西南昌330031)

0 引 言

目前的数字广播电视信号(如数字音频广播(digital audio broadcasting,DAB)、数字视频广播(digital video broadcasting-terrestrial,DVB-T)、数字地面多媒体广播(digital terrestrial multimedia broadcasting,DTMB)和数字调幅(digital radio mondiale,DRM)广播等)大都采用正交频分复用(orthogonal frequency division multiplexing,OFDM)技术,因其类图钉型的波形模糊特性和抗频率选择性衰落能力为雷达提供了良好的照射源,可便利地组建OFDM波形外辐射源雷达[1-6]。此雷达具有以下主要优势:①生存能力强、隐蔽性好;②辐射源分布广泛,较小地受到敌方的影响,抗干扰能力强;③雷达系统简单、尺寸小、方便部署;④不需要频率分配,可以部署在其他雷达不能部署的地方。基于上述优点,OFDM波形外辐射源雷达重新受到人们的重视并逐渐成为研究的热点[7-9]。

外辐射源雷达信号处理通常采用相干处理技术,在接收系统中必须包括参考通道和监测通道,分别用来接收参考信号和目标回波信号。监测通道除了接收目标回波信号外,还不可避免地存在直达波信号和多径回波信号,使得匹配滤波后得到的距离-多普勒(range-Doppler,RD)谱中,目标信号被直达波和多径回波(统称为多径杂波)所掩盖。直达波和多径回波的抑制是外辐射源雷达信号处理需要解决的关键问题。一些参考文献利用最小均方(least mean square,LMS)算法、归一化最小均方(normalized least mean square,NLMS)算法和递归最小二乘(recursive least square,RLS)算法等自适应滤波算法对多径杂波进行抑制,然而这些算法都存在滤波器阶数较多或迭代收敛性的问题[10-14]。同时,在实际应用中多径杂波的条数往往不清楚,常规时域自适应滤波算法的滤波器阶数只能粗略估计,这也将影响杂波抑制的效果。针对上述问题,基于OFDM波形的特点,本文提出了分载波自适应滤波算法,将时域信号变换到载波域,利用同一载频下直达波和多径回波的相关性,在每个有效子载波上分别进行自适应滤波得到目标回波信号。与常规时域自适应滤波算法相比,分载波自适应滤波算法的滤波器阶数恒为1,降低了计算复杂度,便于信号实时处理,提高了自适应滤波性能。

DRM广播作为世界范围内唯一的高频段非专利数字广播,其同样采用OFDM调制方式,在世界范围内覆盖广泛,为高频段外辐射源雷达较为理想的照射源[15-17]。不失一般性,本文将以DRM广播为例来研究OFDM波形外辐射源雷达分载波自适应滤波算法。首先，结合DRM介绍OFDM广播信号的特点和外辐射源雷达接收信号模型；然后，从理论上分析分载波自适应滤波算法的原理；最后，利用仿真数据和实测数据分析比较常规时域自适应算法和分载波自适应滤波算法的性能差异。

1 信号建模

1.1 DRM广播结构

DRM广播是针对30 MHz以下长波、中波、短波波段的新一代数字广播。它采用OFDM技术,可以有效对抗多径干扰产生的频率选择性衰落、多普勒频率漂移等恶劣影响。OFDM是一种多载波调制技术,即同时用多个正交的子载波来传递数据流。实际中一般采用对数据流进行离散傅里叶逆变换(inverse discrete Fourier transform,IDFT)来实现,当子载波数不是2的幂次方时通常采用两边补零做IDFT的方式,其中携带数据的子载波为有效子载波。这些同时传递的数据流组成了OFDM符号的有用部分,再选取符号尾部一段作为循环前缀(cyclic prefix,CP)插入相邻符号间,即可构成一个完整的OFDM符号。以模式B为例,每个OFDM符号的有用部分涉及IDFT的点数为Nu=256,但是有效子载波的个数Ns=207。多个OFDM符号构成一个传输帧,OFDM信号一般以帧为单位传输。DRM标准中定义了5种(A～E)不同的传播模式,分别适用于不同的传输环境[18]。综上所述,DRM基带信号可以表示为

(1)

(2)

式中,k为子载波序号;l为符号序号;r为传输帧序号;S为每帧的OFDM符号个数;kmax和kmin分别是k的上下限;Ts为一个完整OFDM符号周期;Tu为OFDM符号有用部分持续时间,其倒数1/Tu即为子载波频率间隔;Tg为OFDM符号保护时间间隔;Cr,l,k为第r帧中第l个符号内第k个子载波的复调制码元归一化值。

1.2 雷达接收信号时域模型

外辐射源雷达的参考通道用于接收发射站发射的直达波信号,通过对参考通道提纯保证参考信号的纯净性[19]。而监测通道接收到的信号包括直达波、多径回波和目标回波信号等。监测通道回波的时域信号模型[20]可以表示为

τp)+

(3)

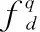
2 分载波自适应滤波算法分析

前文给出了监测通道回波的时域信号模型,本节将分析给出相应的载波域信号模型。将监测通道时域信号按OFDM完整符号划分、去除保护间隔,并对每个OFDM符号有用数据部分进行离散傅里叶变换(discrete Fourier transform,DFT),即将数据由时域转换到了载波域;然后仅保留有效子载波上不同OFDM符号间携带的数据,便得到有效子载波域的监测通道信号,可以表示为

(4)

式中,Yl,k为监测通道信号有效子载波k第l个符号对应的载波域信号采样值;Yl为监测通道信号符号l对应的不同子载波组成的载波域信号向量,可以表示为[Yl,1，…，Yl,k，…，Yl,Ns];Yk为监测通道信号有效子载波k对应的不同OFDM符号组成的载波域信号向量,可以表示为[Y1,k，…，Yl,k，…，YL,k]T;L和Ns分别表示OFDM符号的个数和有效子载波的个数。

下面结合监测通道的时域信号模型和信道传输模型,对Yl中直达波、多径回波、目标回波的成分如下:

(1)分析Yl中直达波部分的表达式

假设直达波的信道传输函数为Adδ(t),根据OFDM技术的原理,发射信号的第l个符号的时域采样dl(t)可以表示为

:T0:lTs

(5)

式中，Cl,k为有效子载波k第l个符号所对应的复调制码元归一化值。

Yl中直达波部分的表达式为

DFT[dl(t)⊗Adδ(t)]=DFT[Addl(t)]=

Ad[Cl,1，…，Cl,k，…，Cl,Ns]

(6)

可以进一步得到Yl,k中直达波对应部分表示为AdCl,k。

(2)分析Yl中多径回波的表达式

以第p个多径回波为例,假设多径回波的信道传输函数为Apδ(t-τp)。Yl中第p个多径回波对应部分可以表示为

DFT[dl(t)⊗Apδ(t-τp)]=DFT[Apdl(t-τp)]=

Ap[e-jω1τpCl,1，…，e-jωkτpCl,k，…，e-jωNsτpCl,Ns]

(7)

同理,可以进一步得到Yl,k中第p个多径回波对应部分为Ape-jωkτpCl,k。

(3)分析Yl中目标回波的表达式

以第q个目标回波为例,Yl中第q个目标回波对应部分可以表示为

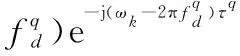
(8)

式中，Dl(ωk)=DFT(dl(t))=[Cl,1，…，Cl,k，…，Cl,Ns]。

(9)

因为在一个符号内的多普勒频移的相位旋度非常小,几乎可以忽略不计,即可近似得到:

(10)

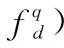
(11)

结合式(8)和式(11),Yl中第q个目标回波对应部分可最终表示为

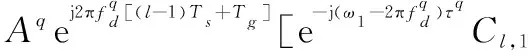
(12)

综上所述,Yl,k的表达式可以写为

(13)

式中,Nl,k为有效子载波k第l个符号的载波域噪声。

接着将有效子载波k对应的L个Yl,k组成向量,Yk的表达式可以写为

(14)

式中

Qk=[C1,k，…，Cl,k，…，CL,k]T

Nk=[N1,k，…，Nl,k，…，NL,k]T

综上对比式(14)和式(3)可见:相比于时域信号s(t),载波域信号Yk成分由4项减为3项,即由于直达波和多径回波部分在时域上仅时延不同,故在载波域上可合并成一项(且与Qk完全相关),而目标回波部分与Uk,q完全相关,且Uk,q和Qk几乎不相关。因此可以利用自适应滤波器分别在有效子载波上进行自适应滤波。以Qk为参考信号,通过自适应滤波器估算系数βk,再将其从Yk中减掉,即为目标回波和噪声项。根据自适应滤波过程的代价函数不同,可采用分载波递归最小二乘(recursive least square by subcarrier,RLS-C)和分载波归一化最小均方(normalized least mean square by subcarrier,NLMS-C)算法。下面分别给出RLS-C和NLMS-C算法进行自适应滤波的具体步骤。

(1) RLS-C算法

步骤1初始化,令Wk(0)=0,Pk(0)=δ-1I,其中δ是一个很小的值,I是一个常数。

步骤2更新:n=1,2,…,L

(15)

(16)

(17)

(18)

式中,λ是遗忘因子;kk(n)是增益因子;Wk(n)是第k个有效子载波进行自适应滤波的滤波器系数;ek(n)是第k个有效子载波行自适应滤波的滤波器输出,即为包含目标信息的载波域信号。

(2) NLMS-C算法

步骤1初始化,令Wk(0)=0。

步骤2更新:n=1,2,…,L

(19)

(20)

(21)

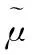
经过上述的自适应滤波处理,对滤除直达波和多径杂波的监测通道的载波域信号分符号进行补零,然后做IDFT变换回时域,将新的时域监测通道信号与对应的时域参考通道信号进行匹配滤波,即可得到滤除多径杂波后目标的相关信息。整个分载波自适应滤波算法流程图如图1所示。

图1 分载波自适应滤波算法流程图Fig.1 Flow chart of subcarrier adaptive filtering algorithm

下面分析上述两种算法实现过程中的算法复杂度。两种算法都要进行DFT、IDFT和自适应滤波过程。如果利用傅里叶蝶形快速算法对监测通道信号L个符号分别作DFT和IDFT,对参考通道的L个符号分别作DFT,一共需要(3/2)NuLlog2Nu次复乘计算。每个有效子载波上进行自适应滤波的迭代次数是L,有效子载波的个数是Ns,两种算法自适应滤波过程的迭代次数都是NsL,但是这两种算法自适应滤波过程的复乘计算量不同。RLS-C算法每次迭代需要8次复乘计算,整个自适应滤波过程进行的复乘次数为8NsL,而NLMS-C每次迭代需要4次复乘计算,整个自适应滤波过程进行的复乘次数为4NsL。所以,RLS-C和NLMS-C算法的总复乘次数分别为(3/2)NuLlog2Nu+8NsL和(3/2)NuLlog2Nu+4NsL。同时,易知RLS和NLMS算法的总复乘次数分别为(4M2+4M)N和(3M+1)N,其中M是自适应滤波器的阶数,N是监测信号和参考信号的时域采样点数。具体推导可参考文献[21]。表1列出了上述4种算法的迭代次数和计算复杂度。

表1 4种算法的参数和计算复杂度

自适应滤波算法的计算复杂度与自适应滤波器阶数和迭代次数有关,常规时域自适应滤波算法的计算复杂度随着自适应滤波器阶数的增加而增加,而分载波自适应滤波算法的自适应滤波器阶数固定为1,两类算法迭代次数相当。虽然分载波自适应滤波算法要对监测通道信号和参考通道信号进行DFT、IDFT会带来一些计算量,但是相比于常规时域自适应滤波器阶数增加所带来的计算量,上述过程显然小的多。因此,分载波自适应滤波算法能够降低计算复杂度。

3 仿真与实测数据结果分析

3.1 仿真数据结果分析

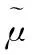
图2是杂波抑制前仿真的监测通道信号与参考通道信号进行匹配滤波得到的RD谱图。从图中可见零频附近存在大量的多径杂波,目标完全被多径杂波所掩盖。图3和图4分别是利用RLS和RLS-C算法对仿真的监测通道信号进行杂波抑制后,与仿真的参考通道信号进行匹配滤波得到的RD谱图。图5是这两种算法处理后目标距离元的截面图。相比于RLS算法,RLS-C算法的自适应滤波器阶数为1,收敛速度快且有较小的输出误差,杂波抑制效果更好,目标的信噪比提升了10 dB左右。图6和图7分别是利用NLMS和NLMS-C算法对仿真的监测通道信号进行杂波抑制后,与仿真的参考通道信号进行匹配滤波得到的RD谱图。图8是这两种算法处理后目标距离元的截面图。同理,NLMS-C算法的自适应滤波器阶数也为1,收敛速度比NLMS算法快,输出误差小,杂波抑制效果好,目标的信噪比提升了5 dB左右。结合上述结果可知,这4种算法都能够抑制多径杂波,使目标凸显出来。然而,RLS算法的复乘次数为1.2×108,RLS-C算法的复乘次数为2.4×106,NLMS算法的复乘次数为6.5×106,NLMS-C算法的复乘次数为2.0×106。图9是仿真数据经RLS-C和NLMS-C算法抑制后的目标距离元截面对比。由于自适应滤波过程的代价函数不同,RLS-C算法比NLMS-C的收敛速度快,收敛精度高。从图9中可见,RLS-C算法有更强的杂波抑制能力,相比于NLMS-C算法,RLS-C算法抑制后目标的信噪比提升了8 dB左右。

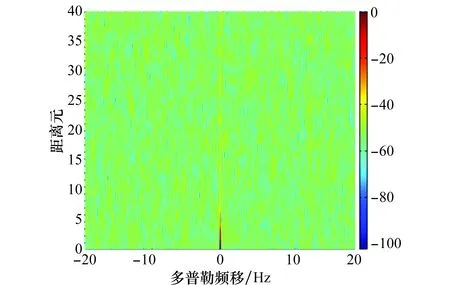
图2 杂波抑制前的RD谱Fig.2 RD map before multipath clutter rejection

图3 RLS算法抑制杂波后的RD谱Fig.3 RD map after multipath clutter rejection by RLS

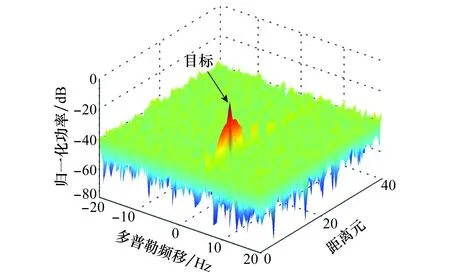
图4 RLS-C算法抑制杂波后的RD谱Fig.4 RD map after multipath clutter rejection by RLS-C

图5 RLS和RLS-C算法抑制后的目标距离元截面对比Fig.5 Normalized target range bin cuts after multipathclutter rejection by RLS and RLS-C

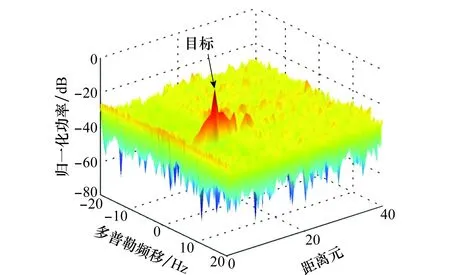
图6 NLMS算法抑制杂波后的RD谱Fig.6 RD map after multipath clutter rejection by NLMS

图7 NLMS-C算法抑制杂波后的RD谱Fig.7 RD map after multipath clutter rejection by NLMS-C

3.2 实测数据结果分析

实测数据是从一个沿海的外辐射源雷达系统中获取的,该雷达系统接收到的DRM广播信号基本工作参数符合DRM标准B模式,发射站和接收站位于青岛市和海阳市沿海,接收站位于海阳沿海,收发站之间的距离约为50 km。接收站的天线为16元线阵,参考通道和监测通道共用接收天线,通过将阵列接收天线波束形成对准发射台和目标方向分别得到参考通道信号和监测通道信号。

图8 NLMS和NLMS-C算法抑制后的目标距离元截面对比Fig.8 Normalized target range bin cuts after multipath clutterrejection by NLMS and NLMS-C

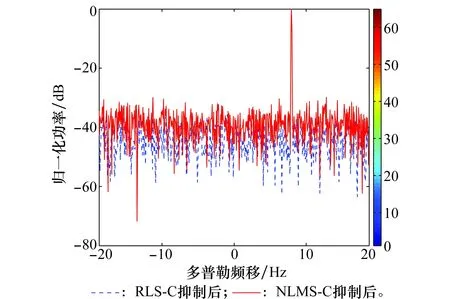
图9 仿真数据经RLS-C和NLMS-C算法抑制后的目标距离元截面对比 Fig.9 Target range bin cuts of simulation data after rejection byRLS-C and NLMS-C

图10是杂波抑制前监测通道信号和参考通道信号进行匹配滤波得到的RD谱,由于多径杂波的影响,目标被完全掩盖掉。

图10 实测数据杂波抑制前的RD谱Fig.10 RD map of experiment data before multipath clutter rejection

图11和图12分别是经过RLS-C和NLMS-C算法抑制杂波后得到的RD谱。这两种算法都能够有效地抑制多径杂波,位于距离元为5,多普勒频移为0.033 17 Hz的舰船目标和海洋回波均凸显出来。图13是实测数据经RLS-C和NLMS-C算法抑制后的目标距离元截面对比。相比于NLMS-C算法,RLS-C具有更强的杂波抑制效果,目标的信噪比提升了4 dB左右。

图11 RLS-C算法杂波抑制后的实测数据RD谱Fig.11 RD map of experiment data after multipath clutterrejection by RLS-C

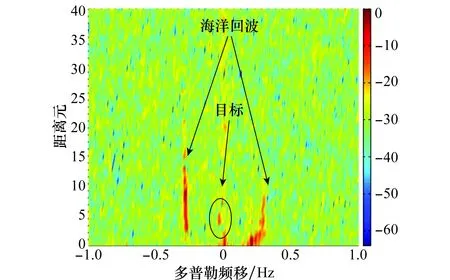
图12 NLMS-C算法杂波抑制后的实测数据RD谱Fig.12 RD map of experiment data after multipath clutterrejection by NLMS-C

图13 实测数据经RLS-C和NLMS-C算法抑制后的目标距离元截面对比 Fig.13 Target range bin cuts of experiment data after rejection byRLS-C and NLMS-C

4 结 论

本文以高频DRM信号为例,研究了OFDM波形外辐射源雷达多径杂波抑制问题,结合时域信号模型和信道特征推导了载波域信号成分组成,在此基础上提出了分载波自适应滤波算法,并给出了所提算法的性能优势对比分析。相比于常规时域自适应滤波算法,分载波自适应滤波算法可将滤波器的阶数降为1,一方面减少了杂波抑制过程的计算复杂度,便于实时处理；另一方面,分载波自适应滤波算法的自适应滤波过程中收敛速度快,具有更强的杂波抑制能力。通过仿真和实测数据证明了分载波自适应滤波算法的有效性。对比RLS-C和NLMS-C这两种分载波算法,RLS-C的杂波抑制效果更好。需要说明的是,本文虽以DRM广播外辐射源雷达为例进行分析,但结果同样适用于其他频段的OFDM波形外辐射源雷达。