石蜡相变熔化过程的实验和数值模拟

蔡莞晨 杨文彬 张 凯 范敬辉 吴菊英 邢 涛 何 韧

(1. 西南科技大学四川省非金属复合与功能材料省部共建国家重点实验室培育基地 四川绵阳 621010; 2．中国工程物理研究院总体工程研究所 四川绵阳 621919)

随着时代的发展，能源需求量越来越大，传统的化石能源有着高碳排放、不可再生的弊端，这些问题在强调环境友好、可持续发展的今天不可忽视，而以太阳能为代表的可再生能源虽然满足了人们对于环保问题的需要，但是在能量供求上存在一种时间-空间不匹配的问题。为了解决这个问题，提出了使用相变储能技术，通过在能量产生时将过剩的能量储存、在需要能量的时候将其释放来解决时间-空间不匹配的问题，提高能源利用率[1]。由于在相变储能过程中受到材料熔化、熔融液体流动、热传导等诸多物理过程的影响，传统的理论方法分析较为困难，故采用数值模拟的方法开展研究。

总而言之，在房屋建筑施工中，施工技术的使用情况会直接影响到整个房屋建筑工程的建设质量，新时期下，随着现代技术的快速发展，房屋建筑施工技术也越来越完善，在具体施工中，施工单位要结合现场实际，合理的选择施工技术，并做好施工管理活动，确保房屋建筑施工效益。

目前有研究者对相变材料开展了大量的研究工作。刘菁伟[2]、田本强[3]制备了石蜡基相变材料，研究了其中的导热填料对于材料导热率的影响。罗李娟[4]在此基础上初步研究了石蜡基相变材料的熔化凝固过程。Hosseinizadeh[5]研究了纳米强化相变材料无约束的熔化。另外也有在相变材料中添加翅片[6]、金属泡沫[7]等加快相变材料熔融的研究。金丽丽[8]研究了石蜡基相变材料在相变墙体上的应用。本文采用Fluent软件建立模型，讨论了网格密度对于模拟结果的影响，在此模型的基础上模拟石蜡的熔化过程，并将结果与相同环境下的实验结果进行对比，讨论了两类结果之间出现差异的原因，分析了石蜡熔融的导热机制。通过对石蜡的模拟，得到了一组可以较好反应石蜡熔化过程的模型及相关模拟参数，可供基于石蜡体系的更加复杂的数值模拟使用。

1 计算模型与边界条件

本文研究的计算模型尺寸和几何结构如图1所示。考虑到石蜡在熔化过程中会发生体积膨胀，故并没有选择让石蜡填充满熔化腔。在完全熔融的情况下，石蜡体液在熔化腔的高度为30 mm，上部为空气。熔化腔四壁温度恒定为55 ℃。熔化腔上壁封死没有物质的流入或流出。熔化壁的内壁设置为无滑移界面。初始压力为大气压，石蜡的初始速度为0，系统的初始温度设置为20 ℃。

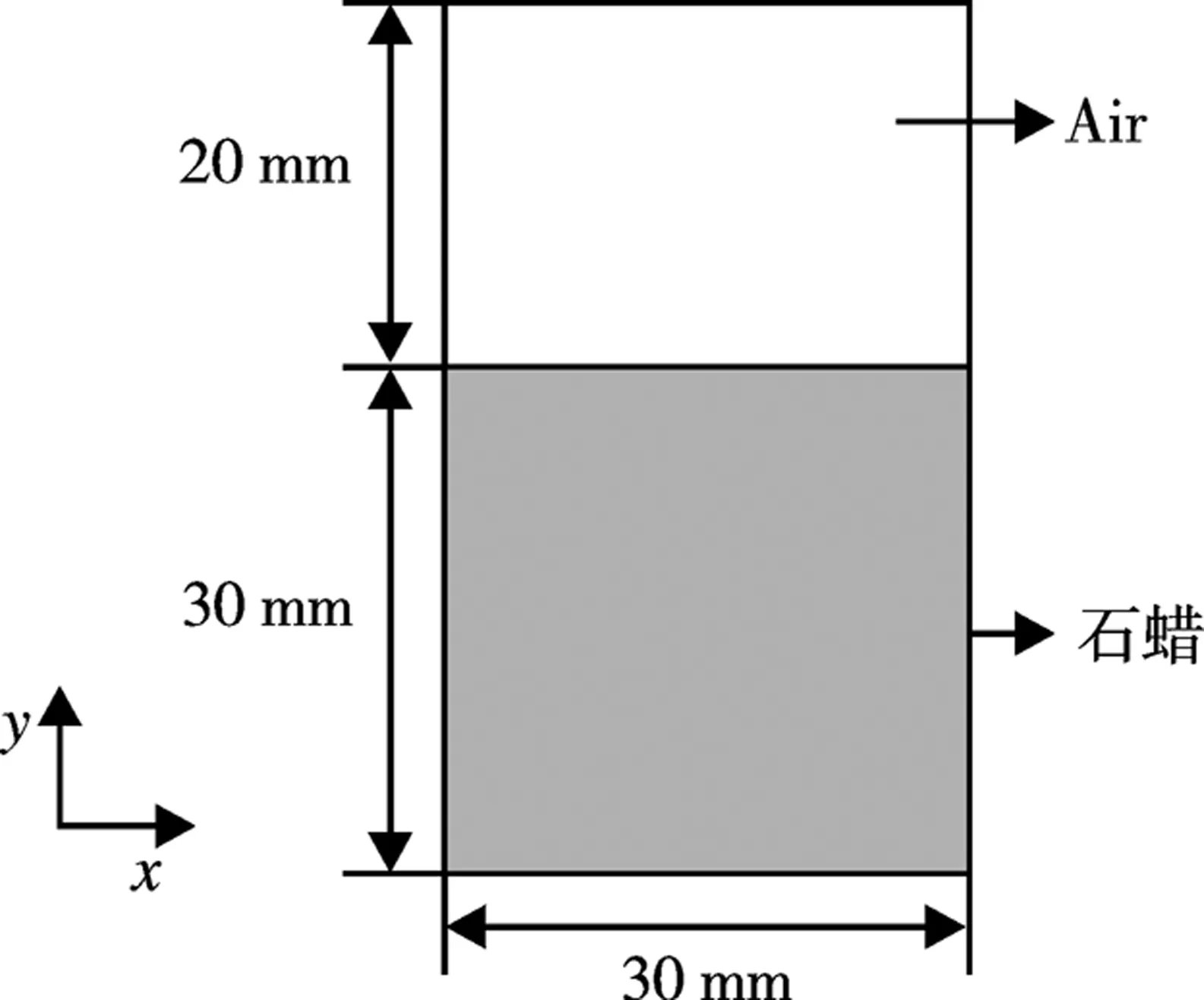
图1 石蜡测试腔模型Fig.1 Simplified model of test cavity of paraffin

实验中所采用的石蜡材料属性列于表1中。考虑到石蜡在熔化阶段时的体积膨胀对于体系的影响，假设石蜡的密度满足Boussinesq假设，所用的热膨胀系数来自于实验测得。

表1 石蜡的热物理性能Table 1 Thermo-physical properties of paraffin

本研究还有如下假设：(1) 熔化的石蜡液体是不可压缩流体；(2) 石蜡的熔化被热传导和热对流控制；(3) 由于熔化是层流导致的流动，黏性消散、热辐射和三维对流可以忽略不计；(4) 石蜡的材料属性受温度的影响可以忽略不计；(5) 相变材料石蜡的密度满足Boussinesq假设，即仅在动量方程的浮力项中考虑体积随温度的变化，引入体胀系数，其他各项及方程中密度为常数。

需要指出的是，本实验之所以使用二维模型并且忽略了三维对流，是为了避免三维模型数学上的复杂性，而且，已有的对于二维模型、三维模型在同一条件下的计算结果以及实际实验结果三者之间的比较也显示，二维模型的模拟具有实际意义[9]。

2 数学模型

动量方程：

7.成果以专业论文形式出版，用以相近专业之间的交流及借鉴，所有培养方案编制成校本教材及指导手册，供学员之间学习使用。

连续方程：

(1)

控制方程如下：

当层间位移角到达6%rad(76.38 mm)循环期间，接近位移极值时，角钢被明显拉起，角钢柱侧钢肢与柱间隙明显。当位移角到达7%rad(89.11 mm)时，随着节点转动角度增大，转动过程中角钢梁侧钢肢变形，与梁产生间隙，前推阶段下角钢加劲肋受压出现屈曲。

围绕四项机制创新，着力深化农村水利重点领域和关键环节改革。适应新型工农关系以及城乡要素平等交换和公共资源均衡配置要求，加快建立健全农村水利投入、组织发动、建设管理和运行管护四项机制，推动农村水利持续健康发展。

4.税务局的信息化建设应继续加强。税务局应加强信息化建设，尽快普及个人通过微信、支付宝、网上电子税务局等途径代开发票，这样可以省去必须到税务局代开发票的麻烦，支付方凭借打印的电子发票即可进行税前扣除。

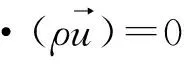
(2)

ΔH=βL

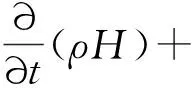
(3)

本文使用的商业有限元模拟软件为AnsysFluent。在Fluent中的melting/solidification模型是基于焓-多孔介质法，它将整个熔融区域看成多孔介质的糊状区域，每个网格内的多孔率ε等于其液相分数β。对于纯固体液相分数为0；固-液混合的模糊区域液相分数介于0～1，纯液体液相分数为1。液相分数β定义为：

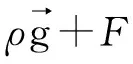
(4)

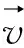
H=h+ΔH

(5)

其中

工业建筑与住宅建筑不同，其内部主要容纳的是工业生产设备，对空间等方面有着比较强烈的要求，这就要求工业建筑设计应该从分重视简单、高效的原则，能够在保证建筑结构稳定的同时，提高内部的利用效率。与此同时，在设计过程中重视各项节能技术的应用，从资源节约入手进行简单化的设计，充分结合实际需求与现场情况，充分发挥高效节能的优势，满足工业建筑多方面内容。

(6)

式(6)中，href为在参考温度Tref时的参考焓，cp为定压比热，ΔH为潜热，介于0～L之间。

能量方程：

(7)

教师：同学们，通过刚刚通读全文之后，相信大家对故事也有了大致的了解，现在谁能用自己的话来说说故事主要讲了什么？可以用分段式，也可以用全文概论式。

F=-A(β)u

(8)

(9)

其中ε=0.001，这是为了避免分母项为0的常数。C=105是糊状区域参数，与熔化的形态有关，Fluent中允许对C值进行调整，一般取105～107[10]。

3 网格独立性验证

为了讨论模拟中网格划分对于结果的影响，对于数值模型所使用的网格，选取了低(150×250)、中(300×500)、高(600×1 000) 3种密度尺寸的网格来进行对比。在网格之外模拟设置都相同的情况下，记录空间中同一点的温度，以此选取较为适合的网格大小来开展实验。计算过程中，中、高两种密度都可以在Fluent默认的计算条件下自然收敛。计算结果如图2所示，从图2可以看出，3种网格密度在相变前和相变后结果几乎完全一样，总体上升趋势相符，在相变过程中3个结果有少许不同，低网格密度的温度上升速度最快，中网格密度的温度上升速度最慢，这种结果的差异是由于在单精度计算高网格密度下，计算的浮点误差对于体系的影响较大，而对于低网格密度，截断误差较大，收敛性能较差。考虑到计算效率，本文选择中网格密度进行计算。

图2 不同网格密度下石蜡熔化的温度-时间曲线Fig.2 Temperature-time curve of paraffin with different mesh density

4 模拟结果与讨论

为了验证模拟计算的有效性，比较在多个相同时刻下石蜡熔化的实验图片与模拟固液相云图，如图3所示。每组图片中左侧为实验图片，右侧为模拟固液相云图，图中红色表示液态，蓝色表示固态，相变材料的熔化过程颜色由蓝色(固态)逐渐变为黄色(糊状)最后变为红色(液态)。在t=240，480，720，960 s时，模拟云图中固相的高度同实验图片中实际液相高度几乎一致，t≈1 200 s时，模拟已经完全熔融，实验中还有些许固体未熔融。

在图3(a)t=240 s中，模拟云图固相区形状整体呈钟形，最上部分固体石蜡由于受到空气对流换热的影响较之两壁熔化石蜡流动的影响较小，使得熔化石蜡的对流换热占据了主导地位，熔融的石蜡在上部侵蚀出了尖角，同时由于高温的液体有着较小的密度，在浮力作用下上升占据了熔融石蜡与空气接触的界面空间。最上部分高温液体与空气之间较小的温差进一步削弱了顶部热空气对于石蜡体系熔化速度的影响。底部加热产生的高温熔融石蜡由于浮力作用上升，与糊状区域进行热交换，之后冷却下降，这样的对称涡流在石蜡底部侵蚀出了对称的圆柱形熔化腔。随着体系熔化的进行，在图3(b)、图3(c)t=480，720 s中，两侧的熔化石蜡热流将固体石蜡上部侵蚀成均匀的圆形，而下部的熔化腔由于熔融石蜡的增加，出现了腔体间合并，直至仅剩两个对称的熔化腔。在此时刻，虽然下部已经有大量熔化石蜡产生，但是由于相变材料特殊的性质，仍有少部分的固体石蜡存在，支持中部的固体石蜡不会由于重力的作用而下沉到底部。在图3(d)t=960 s中,由于下部石蜡熔化过多，无法支撑上部固体石蜡，导致中部固体石蜡结构破坏、下沉，最后产生了固体石蜡在底部的重新分配。此时的石蜡熔化又近似于回到了加热起始时的情况。在图3(e)t≈1 200 s中，石蜡已经接近于完全熔融。

图3 数值计算云图(左)与实验图片(右)比较Fig.3 Numerical calculation cloud chart(left)and experimental photograph(right) at the same time

图4为同一位置实验与模拟熔化时间-温度曲线。图中距离为固态石蜡下测温探针距离石蜡-空气界面的距离。在图4(a)中，模拟数据同实验数据有着较好的符合。但在图4(b)、图4(c)、图4(d)中都出现了在熔化前期模拟数据温度上升比实验上升更慢的现象，这是由于实验中为了记录温度数据而在石蜡中放入了金属探针，探针自身具有一定的导热能力，将外部的热量直接传导入测温点附近的

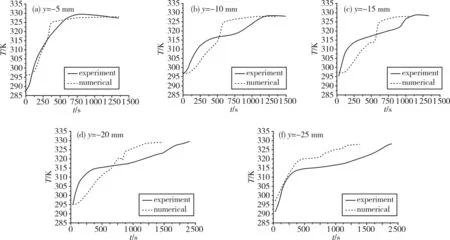
图4 模拟温度-时间曲线与实验结果比较Fig.4 Comparison of numerical temperature-time curves with experimental results

固体石蜡，加速了在熔化前期的温度上升。对比图4(b)与图4(c)、图4(d)，在熔化前期图4(b)实验与模拟的温度差比图4(c)、图4(d)更小，也是由于在图4(b)中金属探针进入石蜡较少，对体系影响较小，而在图4(c)、图4(d)中，由于温度点在固体石蜡较为中心的位置，在模拟中固体石蜡较低的热导率导致只能从周围石蜡中吸收到少量的热量，温度上升速度较低；而在实验中由于金属探针的存在，金属-石蜡的热传导加速了该点的上升速度，这就导致了在熔化初期阶段出现了实验比模拟温度上升更快的现象。在熔化中期，由于中部固体石蜡下沉的影响，在模拟时间-温度曲线上出现了跃升的现象，而在实验时间-温度上，这种现象发生远比模拟上来得要迟，并且跃升得较为舒缓，这是由于金属探针与固体石蜡之间有一定的黏附，阻碍了固体石蜡受重力自然下沉，只有在熔化开展到一定程度的时候，固体石蜡才会从探针上脱落。

北部湾经济区的区内贸易比重反映了其在广西省内贸易中的一个地位，如果这个比重呈上升趋势，则表明广西总贸易对北部湾经济区的区内贸易的依赖程度也在上升。本文主要选取北部湾经济区2008年-2011年四年间全区区内进出口额以及全区进出口总额来进行测度，通过选取指标得到如下表格：

5 结论

本文采用Fluent软件模拟了石蜡的相变熔化过程，并且开展了相同环境条件下的实验，对比了实验与模拟数据，探讨了此模型中石蜡相变过程的传热行为，对模拟与实验间的差异进行了分析。结果表明，石蜡相变熔化过程数值模拟与实验结果可以获得较好的接近，石蜡在熔化过程中的传热方式以自然对流为主。通过数值模拟得到了一组可供基于石蜡体系的更加复杂的数值模拟使用的参数。