基于Hamilton理论的船舶电力控制系统∗

陈炜昕 朱志宇

（江苏科技大学电子信息学院 镇江 212003）

1 引言

船舶电力系统规模和复杂度不断提高，对电力控制系统的要求也相应提高。船舶电力系统本身是一个复杂的非线性系统，与之相应的，使用非线性的控制方法可以达到更好的控制效果［1］，有助于提高船舶电力质量和电力安全。船舶电力系统的核心是船舶电站，现阶段多数船舶电站使用柴油机作为原动机，拖动同步发电机产生电力，进而对全船提供电力，所以要使得船舶电力系统稳定安全，就必须对船舶电站进行合理有效的控制。船舶电力系统的稳定，具体是指如果船舶电力系统在正常运行中受到干扰，如负载突变、局部短路故障等情况，能保持电网各支路与电站相对同步，并持续稳定供电，主要表现为电网电压和频率处于相对稳定［2］。

船舶电力系统因为船舶物理空间限制，成为一个电能高度集中的复杂非线性系统，同时负载与发电机组的各个电力参数具有强耦合、非线性等特点，某些大功率用电设备的启停也会对电网造成明显摄动，控制要求很高，传统以线性理论为基础的设计方法已经很难获得理想的控制效果。因为此类方法处理非线性问题，一般是在工作点附件近似线性化，也可能在模型不精确的情况下近似线性化，必然有自身的局限性。船舶电力控制系统从路上电网控制系统中学习经验并加以修改以适应船舶电力系统特点，如基于Hamilton能量函数的控制方法就是其中之一。该方法从能量角度出发，综合全局考察能量的产生、耗散、传输和转换，以能量的角度设计控制系统，不但具有严格的数学定义，也有符合实际的物理描述［3］，同时直接从非线性的角度进行设计，是一种更为有效的控制方法。

本文使用基于Hamilton能量函数的控制方法设计船舶电力控制系统，设计了船舶柴油发电机组综合控制系统，有效保证了这一动态非线性系统运行的平稳，保证了电力参数的相对稳定。

2 船舶电力系统数学模型

船舶电力系统主要部分包括原动机和同步发电机组成的电站，以及电网传输线路和用电负载等。本文主要针对电站部分进行设计，包括柴油机调系统和同步发电机励磁系统。其系统结构原理如图1所示。

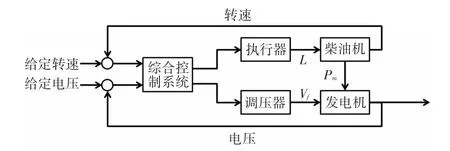
图1 柴油发电机组控制原理图

2.1 柴油发电机组非线性数学模型

执行器以综合控制系统输出信号为输入源u，即柴油机的油门开度，并输出信号轴位移L，作为最终控制柴油机的信号。执行器控制信号与柴油机轴位移传递函数可以表示为［4］

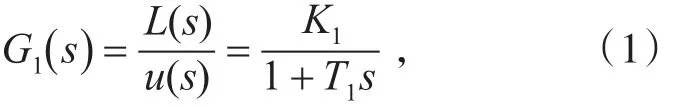
进行拉普拉斯反变换得到：

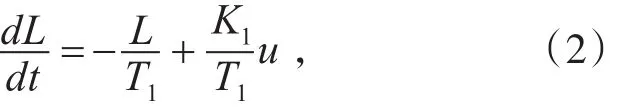
其中，L为执行器的是输出轴位移，u为执行器控制信号，即柴油机的油门开度，T1为执行器时间常数，执行器增益为K1。

2.2 同步发电机非线性数学模型

通过使用不同转动惯量的飞轮，使得柴油机输出力矩控制在较小范围内，近似认为其输出力矩均匀，即

其中，M1为柴油机输出脉动转矩，Mp为一周期内平均输出力矩。

当柴油机阻力矩改变，相应的会引起柴油机的转速产生变动，需要喷油齿杆相应改变，使得转矩转速符合要求，这也就是柴油机调速系统的基本原理。柴油机工作曲线本身是一条光滑曲线，可以使用一些列微小线段来逼近，可以使用m段线段来拟合，记为

其中，i=1，2，……，m；ki，bi是常数，不同分段对应的ki和bi取值不同。柴油机存在一定的空载行程，扭矩输出也有一定滞后，因此其调整特性为

Le为执行器输出轴额定行程，L0为执行器输出轴空载行程，Td柴油机输出力矩的滞后时间。由式（4）和式（5）可得：

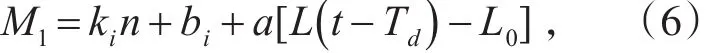
其中，i=1，2，……，m；

则柴油机在额定转速附近时：

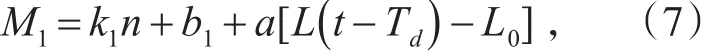
令 d1=b1-aL0，则式（7）可以写为

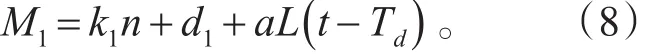
一般情况下，柴油机输出力矩滞后时间很短，也就是Td值很小，可忽略不计［5］，故式（8）可以写为

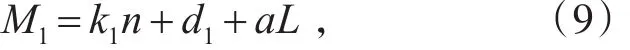
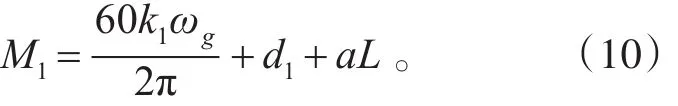
当柴油机输出力矩M1或阻力矩M2（或称柴油机负载转矩）发生变化，相对平衡被破坏，机组运动状态发生改变，此时柴油发电机组运动方程为

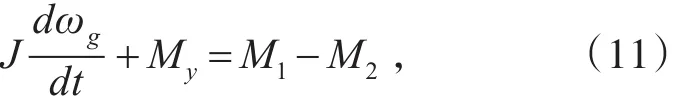
其中，J为全机组转动惯量，含柴油机组、同步发电机组、机械传动装置和其他部分的转动惯量，ωg为柴油机转动轴角速率，My为同步发电机的阻尼力矩。

一般认为同步发电机阻尼力矩My与ωg成正比，则：

其中，K为阻尼系数，与同步发电机组绕组电阻阻值成正比，p为磁极对数。

把式（10）、式（12）代入式（11），于是：

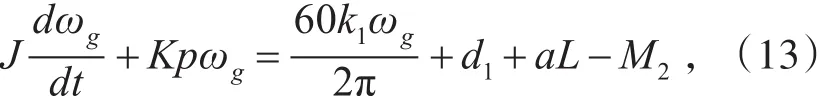
对式（13）进行标幺化，功率基准值选取柴油发电机组的额定视在功率SB，角速率基准值为ω0=100π。得到标幺化后的方程：

同步发电机的输出转矩与柴油机组的负载转矩M2（忽略其空载转矩和绕组耗损），也就是：

其中，Pe为同步发电机的电磁功率，即其输出功率。同时，考虑到一些暂态变化时，转速变化很小，可以认为 ω≈1［6］，所以式（14）可以写为

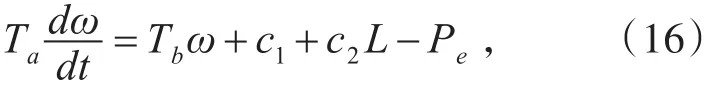
对式（16）两边同时除以Ta，可得：

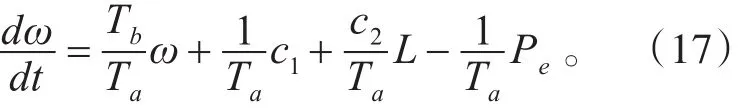
对于船舶电力系统而言，各设备相对集中，输电线路相对较短，且电压等级较陆电系统而言也相对降低，因此可以忽略变压器电抗以及传输线路电抗等，此时三相同步发电机输出功率为

其中，ua，ub，uc为三相电压，ia，ib，ic为三相电流。

转换到dq0坐标系中，式（18）对应的功率标幺值为

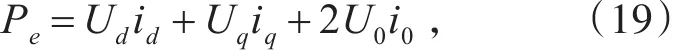
如果电机定子绕组使用Y连接，正常运行时三相平衡没有中线，那么i0=0，式（19）表示为

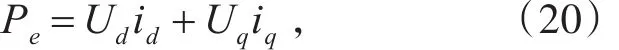
船舶电网供电距离相对较短，传输线路压降和损耗相对较低，可以忽略传输阻抗［5］，则同步发电机电流：

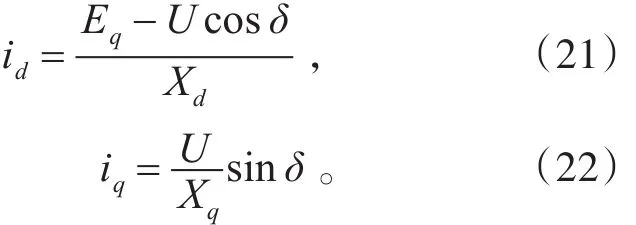
另外，船舶使用的发电机组都是凸极同步发电机，d轴同步电抗 Xd和d轴暂态电抗不等，即'，将式（21）和式（22）的电流 id和 iq代入式（20）可得机组有功功率输出方程：

由式（25）、式（18）和式（24）、式（21）、式（22）可得柴油发电机组转子运动方程：

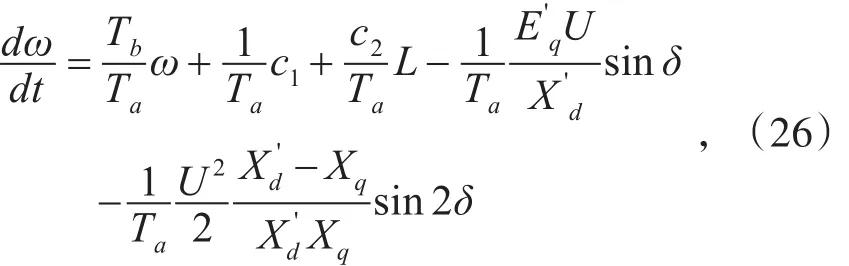
在忽略柴油发电机组暂态凸极效应和饱和后，且机组处于额定转速附件运行，可得发电机的励磁绕组暂态方程：

将式（26）代入式（27）可得励磁绕组的动态方程：

综上，由式（19）、式（26）、式（2）和式（27）得出船舶电站柴油同步发电机组非线性数学模型：

3 基于Hamilton理论的综合控制系统设计

3.1 理论简述

基于Hamilton理论设计的控制器，不仅具有较为完善清楚的物理意义，也可以直接从非线性角度分析和处理问题，非常适用于设计船舶电力系统控制系统。

对于仿射非线性系统［7］：

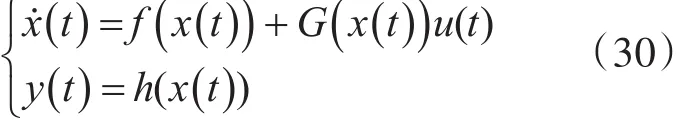
其中，x∈Rn是状态变量，u为控制输入信号，y为输出信号，为适当维数的函数

矩阵或函数向量。

定义1 对于仿射非线性动态系统（30），若存在有下界函数H(x)，使其可以表示成：

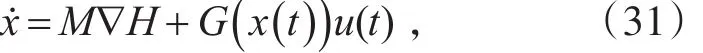
引理1 如果广义受控Hamilton非线性系统（30）可以表示为

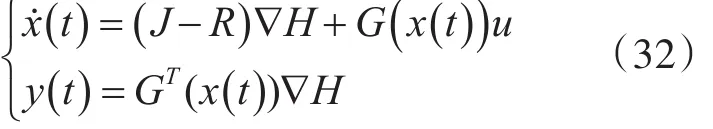
其中，J(x)为斜对称矩阵函数，R(x)为半正定矩阵，且系统（32）满足零状态可检测条件，则在该条件下系统存在反馈控制率：

其中，K为控制增益矩阵，为使系统（30）渐进稳定在某一需要的运行状态的平衡点附件，K应为正定矩阵。

所以，可以依据引理1借助Hamilton能量函数，同时设计合理的反馈，令系统稳定或渐进稳定在特定平衡点。这便是基于Hamilton能量函数设计控制器的理论基础。

3.2 综合控制器设计

现在，根据上述设计方法，为系统（29）设计综合调速励磁控制系统。

可得：

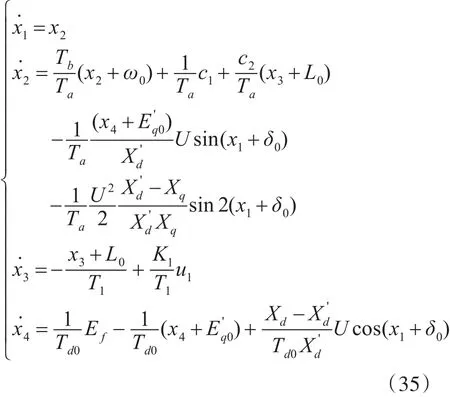
为其构造Hamilton能量函数H(x)：

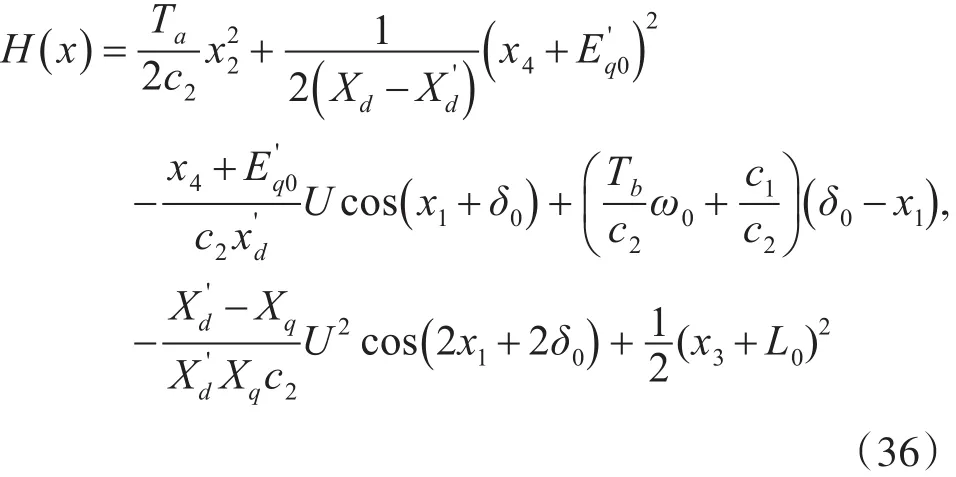
根据式（36），

由此可将原系统动态模型转换为广义受控Hamilton系统的形式：

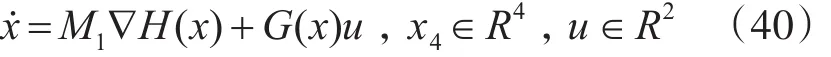
通过观察发现，M1不符合式（32）的形式，为满足引理（32）结构，为其设计一个预反馈：

其中，v1是一个新定义的参考输入，于是原系统（29）变为形如引理（32）的形式：

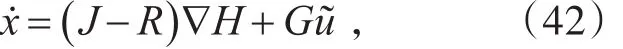
根据引理（32），式（42）的输出方程为

考虑预反馈（41），结合式（33）可得综合控制律：

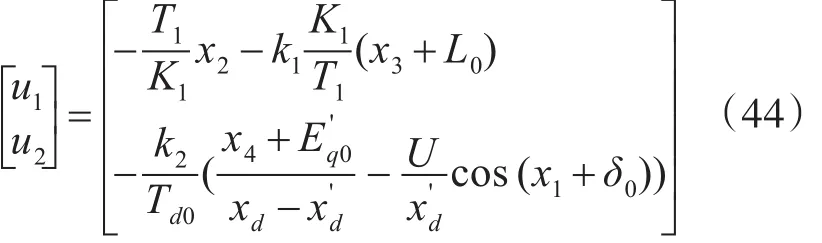
将式（44）代回原系统（35）可得：

于是由引理（32）可知系统（46）渐进稳定。

4 仿真分析

仿真所需的系统相关参数如下表。

表2 同步发电机参数

首先验证系统不加负载时，空载启动特性，结果如下。

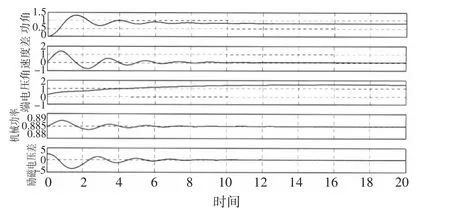
图2 柴油机主要参数变化曲线图

其中，油门开度的偏差值u1曲线如图3。

图3 油门开度偏差值变化

励磁电压偏差值u2曲线如图4。

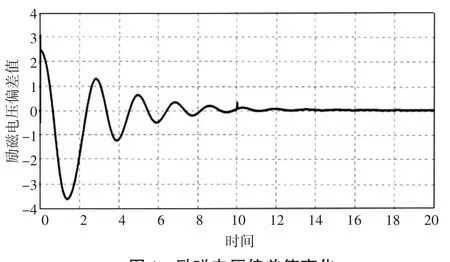
图4 励磁电压偏差值变化

由图可以看出，发电机组各项参数可以较好地达到所需状态并保持相对稳定。

现在进一步地模拟日常航行中改变接入负载的情况，即突增突减负载，观察控制系统效果，在发电机组启动后，15s时突然增加一半的负载，变化曲线如图5。

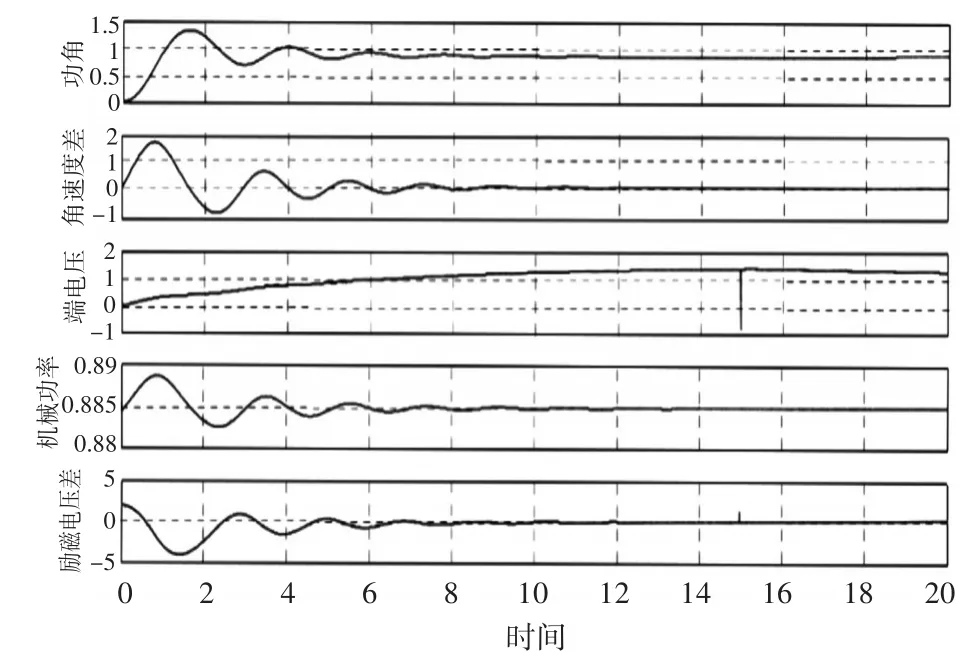
图5 突加负载各参数变化

类似的，验证突减一半负载时的系统控制效果，15s时减载，变化曲线如图6。

由此可以看出，基于Hamilton理论设计的综合控制系统，在负载变动等情况下，系统基本能较快恢复相对稳定，保证电网各项参数处于正常水平，具有良好的控制效果，可以保证船舶电力系统的安全稳定运行。

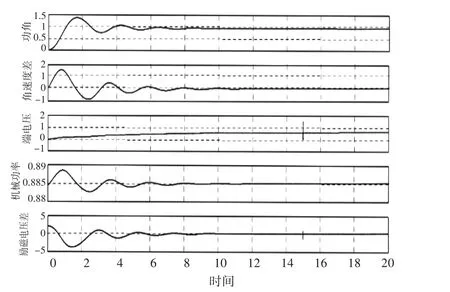
图6 突减负载各参数变化

5 结语

本文针对船舶电力系统非线性的特点，设计了一种基于Hamilton理论的船舶电力综合控制系统，该方法直接使用非线性的方法分析和设计控制器，适合船舶电力系统这样的典型非线性系统。仿真结果表明，所设计的控制系统能有效抑制负载变动带来的影响，使船舶电网处于相对稳定的状态运行，有助于提高船舶的用电安全和用电品质。