基于融合算法的多参数雷达信号分选∗
2018-09-27张友益王玉梅
陈 恒 张友益 王玉梅
(1.江苏科技大学 镇江 212001)(2.中国船舶重工集团公司七二三研究所 扬州 225001)
1 引言
信号分选是电子支援系统(ESM)中的重要技术,是实现雷达辐射源识别的重要基础。传统的多参数信号分选技术是依次利用脉冲到达角、重频、载波频率及脉宽等信息对雷达全脉冲序列进行去交错,然而在高脉冲密度和大量复杂形式脉冲交叠的情况下,这种分选策略显然是低效的[1]。因为这种传统处理方式的分选效率是由上述处理过程中每一级的分选准确率来决定的,其最终的分选结果可能使属于同一辐射源的脉冲序列被分割到不同的集合中,而分属于不同辐射源的部分脉冲被组合到同一个集合当中,即产生了增批[2]和漏批现象。
一些学者引入新的算法进行多参数分选,比如林志远将Kohonen神经网络应用在雷达多目标分选中,取得了很好的分选效果,但这个分选是建立雷达脉冲参数完全不相交的情况下[3];还有Joshua[4]和 Krishna[5]提出的 k-means算法,虽然简单有效,但是对聚类个数和聚类中心依懒性很大,而且孤立点对分选的效果有很大影响。这两种方法虽然都可以用于信号分选,但是约束条件太多,而且对于雷达参数交叠比较严重的情况无法准确分选。
本文首先针对当前信号环境的复杂和传统分选算法的不足作了简要分析,然后介绍了自组织特征映射神经网络二维结构和学习步骤,其次对k-means算法的聚类原理[6~8]以及它的优缺点进行了简要分析,提出基于SOFM网络联合k-means算法的雷达信号分选方法步骤,最后分别利用这三种算法对复杂交错的相同雷达辐射源数据进行了分类。
2 二维阵列自组织特征映射(SOFM)网络
SOFM模型可以用二维阵列表示,这种结构如图1所示。二维阵列神经网络由输入层和竞争层组成。输入层是一维的神经元。竞争层是二维的神经元。输入层的神经元和二维阵列竞争层的神经元每个都相互连接。二维阵列竞争层也称输出层。

图1 二维SOFM阵列模型
在二维阵列竞争层中,可以清楚看出:每一个输出神经元都和最近相邻的8个神经元相连。当然,最边沿的神经元和3~5个神经元相连,但这只是最边沿的神经元才会这样。而从二维阵列内部一般是每个输出神经元和8个最相邻的神经元相连。
SOFM网络[9~11]模型的学习算法步骤如下:
1)初始化。对网络的输出层各权向量赋一个小的随机数,得到初始化各个神经元的邻域Njc(t)。
2)接受输入。从样本中随机输入一个样本模式作为网络的输入样本Xi,i=1,2,…,n。
3)寻找获胜神经元节点。计算输入样本与所有输出层神经元之间的欧拉距离,从中选出距离最小值所对应的神经元,即为获胜的神经元节点,满足下式
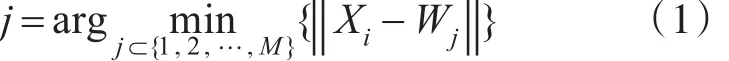
4)调整权值。获胜神经元j的邻域Njc(t)内的所有神经元进行调整:
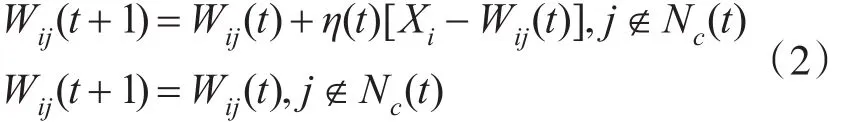
5)返回步骤2),直到学习速率η(t)小于某个预定的值或兴奋神经元与输入样本稳定对应为止。
SOFM是一种无导师的学习人工神经网络,能够对不同的输入样本模式进行学习,将不同的输入模式有序地映射在输出层上,其权值反映了输入数据模式的分布特征,即可利用SOFM对数据进行特征提取。
3 k-means算法
J.B.Mac Queen在1967年提出的k-means算法到目前为止是用于科学和工业应用中诸多聚类算法的一种极具影响的技术。其有快速收敛、计算简单、分类迅速及占用计算机内存小的优点,传统k-means算法以误差平方和准则函数作为聚类的结果函数,误差平方和准则函数定义为
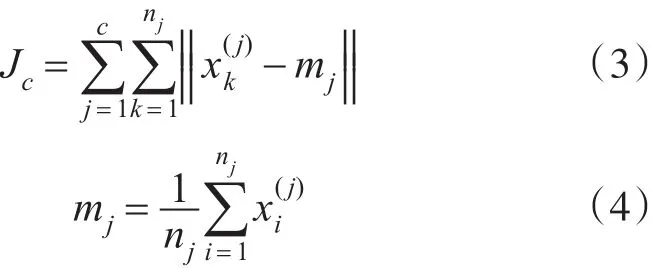
式(3)中的 Jc表示误差平方和,式(4)中的 mj,j=1,2,…,c,是聚类类型xj中所含样本的平均值,表示c个聚类的中心。在样本x给定的情况下,Jc的大小取决于c个聚类中心的值。当n个样本聚类为c类时,Jc表示聚类时总的本样误差平方和。Jc的大小,表明误差的大小,误差越大,说明聚类的结果越差,因此应寻求使Jc最小的聚类结果,即在误差平方和准则下的最优结果。
k-means算法的工作原理[12]:根据输入的参数k,将数据集划分为k个簇,首先在样本数据集中随机选取k个数据点作为初始聚类的中心,再将各样本点到每个聚类中心的欧式距离算出,并选择距离最近的某一聚类中心,将样本归并到该聚类中心所在的类。最终在新形成的所有聚类中,计算各自所含数据对象的平均值,即为新聚类的中心。若在相邻的两次聚类中,发现各聚类中心均无任何变化,则说明样本调整结束,聚类准则函数已收敛。
但k-means算法也有以下不足之处,聚类结果依赖于聚类个数k的初始设定;初始聚类中心是随机选取的,由于初始选取点的不同,可能会出现不同的聚类结果,且容易陷入局部最优聚类;聚类结果对噪声点和孤立点过于敏感,因采用同一个聚类中所有对象的平均值作为聚类中心,所以算法的效果受到噪声和孤立点的影响较大。
4 OFM网络和k-means算法的融合算法
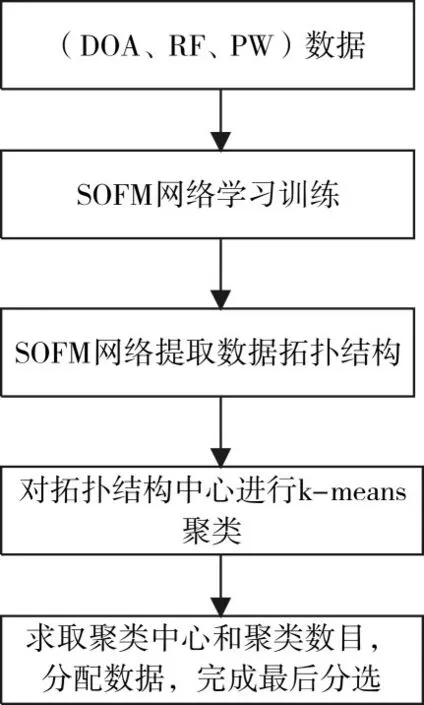
图2 组合聚类算法流程
本文提出的自组织特征映射神经(SOFM)网络和k-means算法的融合算法。该方法主要采用先分后合的思想,意在先用SOFM网络将脉冲参数分成多个模块,特别是在脉冲参数交叠的地方,然后计算这些模块的质心,利用k-means算法对这些质心再分类,最后对应相应的模块进行统计,得出最终的分类结果。
这种组合算法的优点:首先,自组织特征映射神经网络在学习训练之前需要提前确定拓扑结构的规模,该算法则不需要确定具体的规模;其次,该算法中利用SOFM网络只需提取数据的拓扑结构即可,不需要运行到最后节省了时间;再者,提取后的拓扑结构的中心数量少,大大地降低了k-means的运算量,还可以避免孤立点的影响;最后,一般的分类算法对于交叠在一起的数据,只会按照距离远近原则归为一类,而组合算法则可以降低这种将不同的数据聚集到一类的概率,从而达到更高的分选准确率。
算法的具体步骤如下:
1)首先以到达角(DOA)、载频(RF)、脉冲宽度(PW)为基准产生脉冲描述字数据,要求是这些数据之间交叠严重,并且对数据进行归一化(三个参数的单位不一致);
2)然后执行SOFM网络算法,将待聚类的数据输入到SOFM网进行训练;
3)SOFM网络训练结束后,网络通过自组织方式对雷达脉冲序列进行初始聚类,得到一个拓扑结构,这样做的好处就是可以将大数据的分类划分成多个小模块,避免了一些数据交叠比较严重而造成分选准确率较低的情况;
4)提取上一步中得到的拓扑结构各模块的中心向量作为k-means算法中的初始中心向量来使用。设定k值,运行k-means算法。最后根据聚类结果,对应拓扑结构,分配数据,完成最后的分选。注意:拓扑结构中显示的数据是每个神经元周围的数据。算法的具体流程图如图2所示。
5 仿真实验及结果
根据雷达辐射源环境及信号模型的特点,在不考虑信号脉内特征的情况下,选取脉冲的3个基本参数(RF、PW、DOA)组成输入特征向量,根据雷达信号模型产生4类变化复杂的雷达信号,生成交叠严重的全脉冲仿真数据,以高斯随机变量模拟RF、PW、DOA参数的测量误差。雷达参数的具体信息如表1所示。

表1 雷达参数信息
根据表1中的雷达参数,首先生成4部雷达的信号数据作为待分选识别的雷达信号样本,且训练数据和待分选的雷达信号样本都做一定的丢失处理,更符合实际情况。图3为4部雷达三参数交叠之后的分布情况。
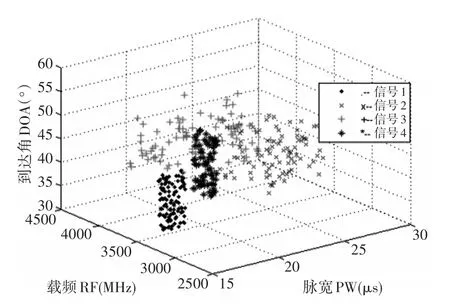
图3 数据的三维分布
由上面图3可以发现,4部雷达的3个常规特征参数都存在严重的交叠现象。本文根据这些雷达辐射源参数,分别利用自组织特征映射神经网络算法、k-means算法以及这两个算法融合后的算法做了三个仿真实验。
5.1 仿真实验一
单独利用SOFM网络对上文设定的雷达辐射源数据进行分选。输入层的维数为3,输出层也即竞争层为2*2。对给定的雷达辐射源数据进行训练,SOFM网络提取的雷达辐射源参数拓扑结构如图4所示,图5是聚类之后的一个结果图。可以看到,虽然把数据分成了四类,但是分类结果不是很理想,通过这些数据并不能很好地区分出原始信号。

图4 SOFM网络拓扑图
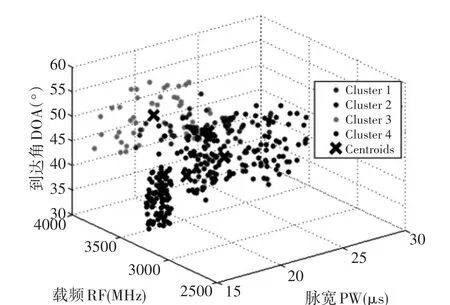
图5 SOFM网络分类图
5.2 仿真实验二
单独采用k-means算法相同的雷达辐射源数据进行仿真。因为辐射源的数目为4,所以这边k设定为4。按照k-means算法聚类步骤,进行仿真分选,分选结果如图6所示。从图6中可以看到,分选结果和SOFM网络分选结果类似,有一类数据特别大,造成这种情况的主要原因是参数交叠严重,导致这两种算法误将另外三类数据分到该类当中。所以,单一的分类器对于雷达辐射源数据交叠比较严重的情况则显得不是很合适,分选结果达不到要求。
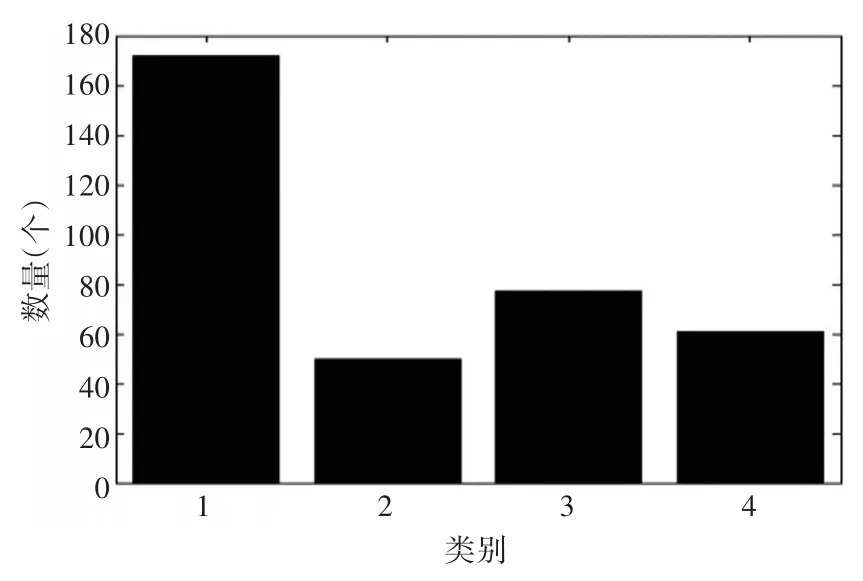
图6 k-means算法分选结果图
5.3 仿真实验三
利用SOFM网络和k-means算法联合后的算法对相同的数据进行分选。输入层的维数是3,竞争层采用4*4的网络规模,先对数据进行训练,然后SOFM网络提取数据扑结构,如下图7所示。

图7 SOFM网络拓扑图
提取上图中拓扑结构各模块的中心向量,利用k-means算法进行再次聚类,这里的k值取4,拓扑结构的中心向量聚类结果如图8所示。
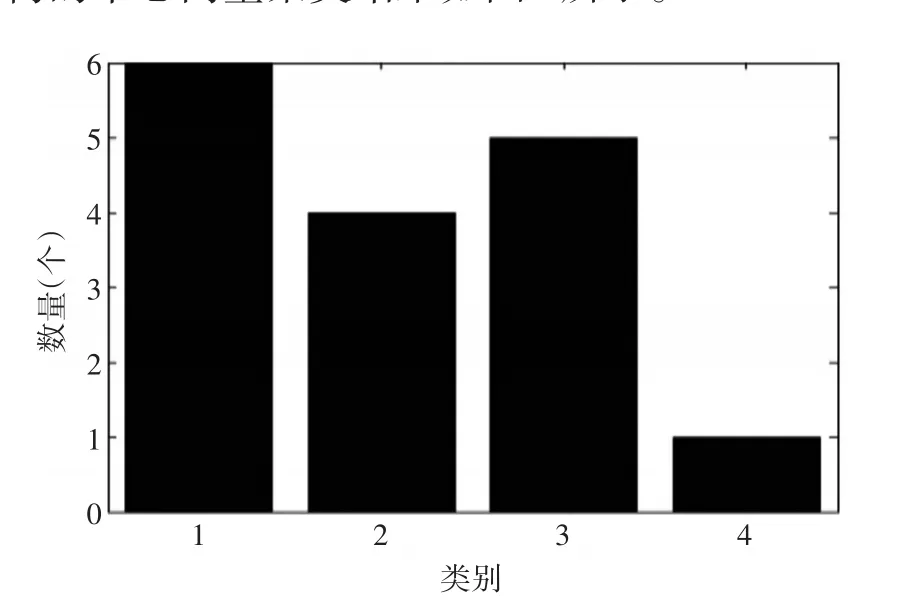
图8 k-means算法聚类图
由上面两图可以看出,这种组合聚类方法很好地将数据分成了四类,结合图7和图8的仿真结果,对最后的分选结果进行了统计。然后和仿真实验一和二的仿真结果进行了对比,如表2所示。
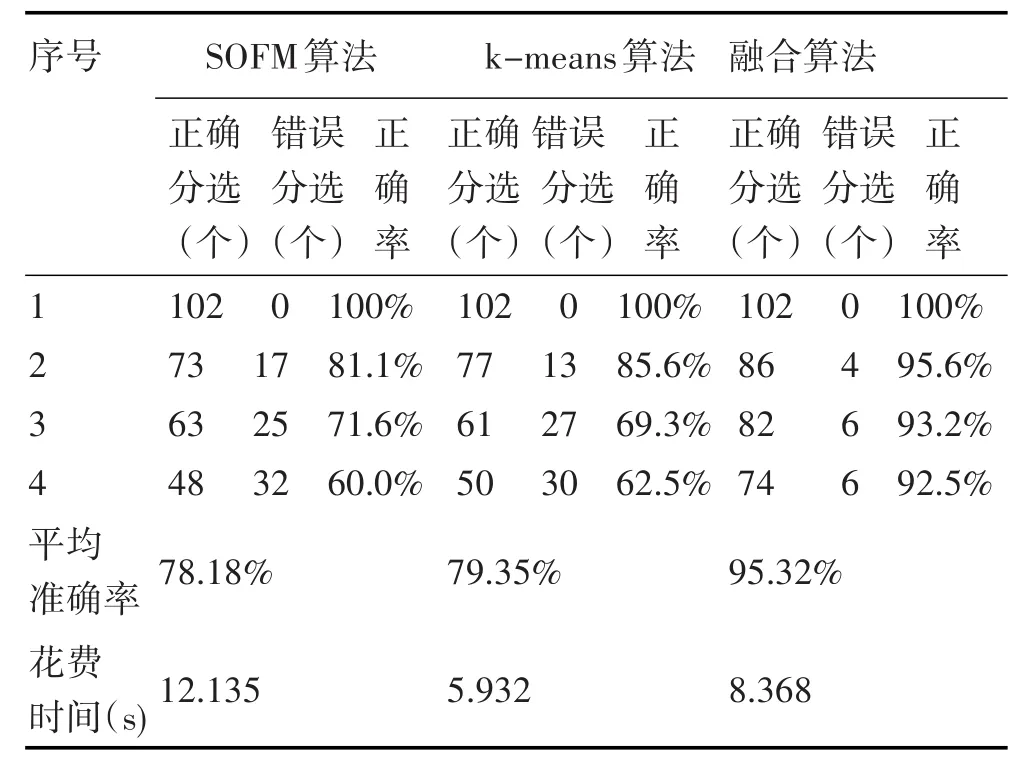
表2 仿真数据的对比结果
表2是三种聚类方法分别对雷达辐射源三参数数据聚类准确率以及仿真时间的对比,可以发现,在面对4类这种参数交叠严重、变化复杂的信号时,本文提出的基于SOFM网络联合k-means算法的雷达信号分选方法对各个类别雷达信号的分选准确率以及总体平均正确率都远高于其他两种方法,并且所花费的时间小于SOFM聚类算法,实时性提高。仿真结果验证了本文提出的基于SOFM联合k-means算法的雷达信号分选方法针对密集脉冲密集的交叠信号分选的有效性。
而对于仿真实验三中SOFM网络竞争层采用4*4的规模,是因为不同的网络规模对分选准确率有不同的影响,因此,特采用不同的网络规模对相同的雷达辐射源数据进行仿真,并对分选准确率作了统计,结果如图9所示,可以发现当采用4*4的网络规模时,分选准确率最高,而网络规模超过这个规模时,分选虽然发生了变化,但是变化幅度不是很大,逐渐趋于平稳。
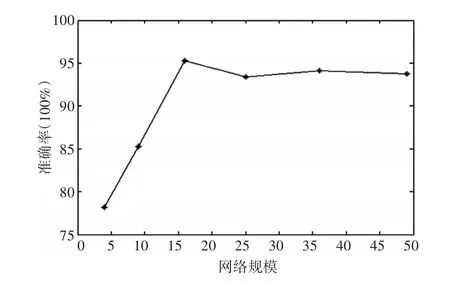
图9 不同网络规模对应的分选准确率
6 结语
单一分类器在雷达信号分选中存在很大不足的主要原因在于电磁环境复杂,参数交叠严重。而本文提出的融合算法可以结合两个分类器的优点,互相弥补不足,仿真结果证明,这种融合算法比单一分类器的分选效果要好,但这种方法对于不同的电磁环境还要作具体的分析。
