形数法测定杉木人工林单木材积误差分析

林久光

（福建省武夷山市林业局，福建 武夷山 354300）

单株立木材积测定方法有多种，比较实用的一种方法是通过形率的测定推算形数，再按立木材积三要素计算材积[1-2]。该法的理论依据是立木材积等于胸高断面积、树高、形数这三个要素的乘积，其关键技术是形数的确定。为此，林业工作者对形数与形率的关系作了许多研究，提出了多种形数与形率的关系式，主要有：形数等于形率的平方、形数等于形率减去一个常数、希费尔公式、书斯托夫式[1-6]。然而，利用这些关系式推算形数并计算材积，其精度如何？对杉木人工林而言，未见相关报道。基于此，本文采用样木实测数据，对上述通过形率推算形数并测定杉木人工林单木材积的方法进行误差分析，并试图提出改进方法，以其为提高单株立木材积的测定精度提供有价值的参考依据。

1 研究数据与方法

以样木材积、胸径、树高、形数、中央直径以及形率等实测数据，来检验形数法测定立木材积多种方法的误差，对其进行分析比较。

1.1 样木采集

在南平市杉木人工林分布区中采集样木实测数据。为减少工作量和对林分的破坏，样木数据结合木材生产采集。每株样木伐倒后，量测树高、胸径、中央直径，统一以1 m为一个区分段长度，测定各区分段中央直径及梢头木底直径，用中央断面区分求积式计算样木带皮材积，其中梢头木材积用圆锥体体积公式计算。共计343株杉木样木，主要测树因子分布范围为：胸径5.4~38.0 cm，树高4.5~28.9 m，材积0.008 1~1.246 0 m3，形数 0.338~0.788，形率 0.406~0.927。

1.2 立木材积测定方法

立木材积等于立木材积三要素的乘积，公式如下。

式中：V为立木材积；g为胸高断面积；h为树高；f为胸高形数，简称为形数。

在森林调查中，用围径尺测定胸径并计算胸高断面积，用测高器测定树高，给定合适的形数，即可用上式计算出立木材积，该法称为立木材积测定的形数法。问题的关键是，形数作为计算树干材积的一个重要换算系数是无法直径测出的。预测形数的方法之一是根据形数与形率的关系，通过形率测定推求形率。在我国，最常用的形率是胸高形率，一般所说的形率即指这种，表达式如下。式中：d1.3为胸径；d1/2为中央直径。

由测树学知识可知，常用的形数与形率关系式有如下 4 种[1,6]：(1)形数等于形率的平方，f=q2；(2)形数等于形率减去一个常数，f=q-0.2；(3)希费尔公式，f=0.14+0.66q2+0.32/(qf)；(4)书斯托夫式，f=0.6q+1.04/(qf)。测定树干中央直径和胸径，按第(2)种计算形率，再代入形数与形率关系式，求得形数，用第(1)种计算树干材积。为便于说明问题，把第(3)种至第(4)种推算形数进而计算单株材积的方法依次称为方法一、方法二、方法三、方法四。

1.3 误差指标

以中央断面区分求法测定的材积为实际值，形数法测定的材积为测定值，计算单株误差P、平均系统误差S（简称系统误差）、平均相对误差绝对值E（简称平均误差），公式如下。

根据上述误差指标对各种材积测定方法进行分析评价，并对其进行改进。

2 结果分析

2.1 整体误差分析

利用样木资料，用前述四种材积测定方法计算材积测定误差并统计误差分布状况，结果见表1。

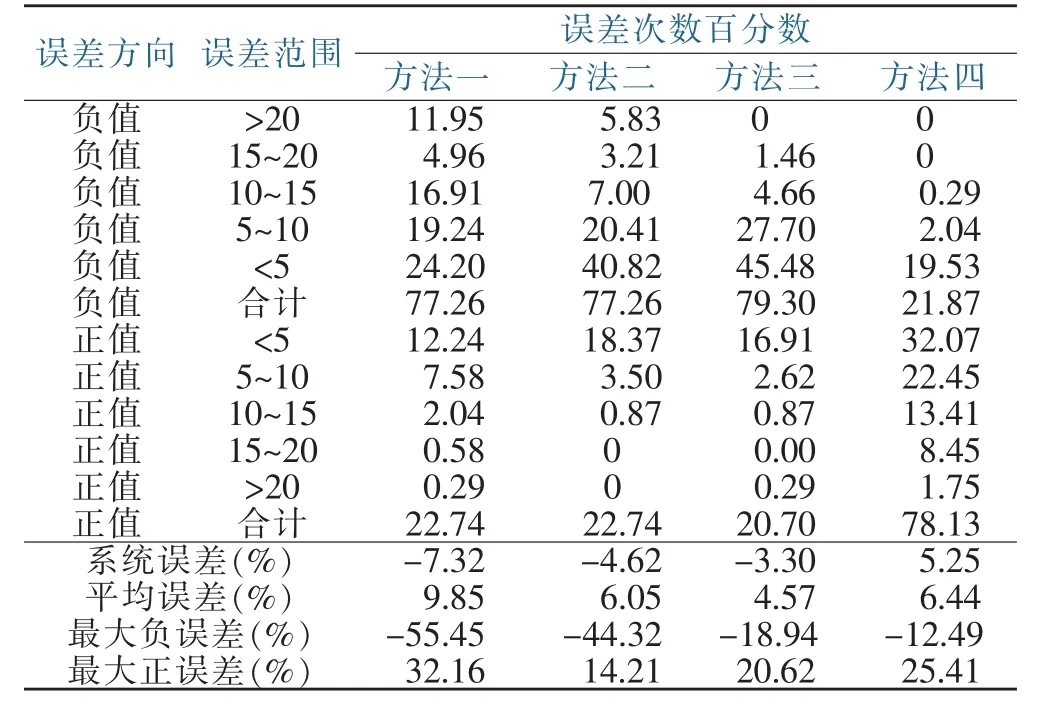
表1 误差分布情况Table 1 Error distribution

分析表1可知，方法一负误差次数百分数为77.26%，最大负误差为-55.45%，正误差次数百分数为22.74%，最大正误差32.16%。显然，负误差次数大大超过正误差，其负误差值大于正误差，说明材积测定值多数情况下小于实际材积。从误差大小来看，正负误差在5%范围内所占比例为36.44%，正负误差在范围内10%所占比例为63.27%，即有36.73%的测定误差超过10%，表明方法一用于测定立木材积，其准确性是不高的。系统误差用于反映整体测定值是否存在系统性偏大或偏小的趋势性误差，这一指标越接近于零越好，一般要求小于正负3%，但方法一测定材积的系统误差达到-7.32%，明显小于整体实际材积，且与实际值相比偏差太大。平均误差用于反映测定误差的单株平均水平，要求该指标等于零是不可能的，只能是越小越好。方法一的平均误差为9.85%，也显得偏大。

方法二负误差次数百分数也是77.26%，正误差次数百分数为22.74%，这一点与方法一相同，均是负误差次数大大超过正误差，按误差绝对值来衡量，是负误差值大于正误差，说明材积测定值多数情况下小于实际材积。但是，方法二最大负误差为-44.32%，最大正误差为14.21%，小于方法一的最大正负误差。从误差大小来看，正负误差在5%范围内所占比例为59.18%，正负误差在范围内10%所占比例为83.09%，表明误差超过正负10%的次数所占比例小于20%，其测定精度高于方法一。方法二测定材积的系统误差达到-4.62%，同样是小于整体实际材积，与方法一相比，虽然误差小于方法一，但与实际材积相比，差异性还是明显的。方法二的平均误差为6.05%，明显小于方法一。

方法三负误差次数百分数为79.30%，最大负误差为-55.45%，正误差次数百分数为20.70%，最大正误差20.62%，这些指标与方法一和方法二相同，都是负误差次数大大超过正误差，说明材积测定值多数情况下小于实际材积，偏小幅度即为系统误差，该值为-3.30%，一定程序上存在趋势性偏差。从误差大小来看，正负误差在5%范围内所占比例为62.39%，正负误差在范围内10%所占比例为92.71%，表明误差超过正负10%的次数所占比例小于10%，平均误差为4.57%，其测定精度明显高于方法一和方法二，达到了较高的测定精度。

方法四负误差次数百分数为21.87%，最大负误差为-12.49%，正误差次数百分数为78.13%，最大正误差25.41%。这些指标与前述三种材积测定方法相比，刚好相反，是正误差次数大大超过负误差，其数值也大于负误差，表明材积测定值大多数情况下大于实际材积。从误差大小来看，正负误差在5%范围内所占比例为51.60%，正负误差在范围内10%所占比例为76.09%，即有23.91%的测定误差超过10%。系统误差5.25%，平均误差6.44%，这二个指标小于方法一，大于方法三，与方法二接近，但方法四测定结果多数大于实际材积，这一点与前述三种方法刚好相反。

综合上述分析，按照误差分布情况，以及系统误差和平均误差的大小，可以认为方法三精度最高，方法一精度最低，方法二和方法三的材积测定精度接近，位于方法一和方法三之间。

2.2 各径阶误差分析

把所有样木材积测定误差按径阶（2 cm为组距）归组，计算各径阶系统误差和平均误差，结果见表2。

分析表2可知，方法一的材积测定误差在16,18,20,22 cm径阶处最大，向两端逐渐减小，其他三种方法则是胸径小误差大，胸径大误差相对小，胸径达到24 cm径阶以后，系统误差绝大多数小于正负3%，个别径阶例外。方法四各径阶的系统误差均为正值，即测定材积整体上均大于实际材积。其他三种方法刚好相反，各径阶的系统误差基本上都小于零，表明材积测定值偏小。在所有样木中，最大胸径为38厘米径阶，测定误差情况与上述有出入，但只有一株样木，不足以说明问题。

从平均误差来看，方法一各径阶误差均大于其他三种方法，方法二和方法四基本上差不多，而方法三大多数径阶的误差小于方法一、方法二和方法四，进一步证实方法三的测定精度高于其他方法。

2.3 各树高级误差分析

以2 m为级距把所有样木材积测定误差按树高级归组，计算各树高级系统误差和平均误差，结果见表3。

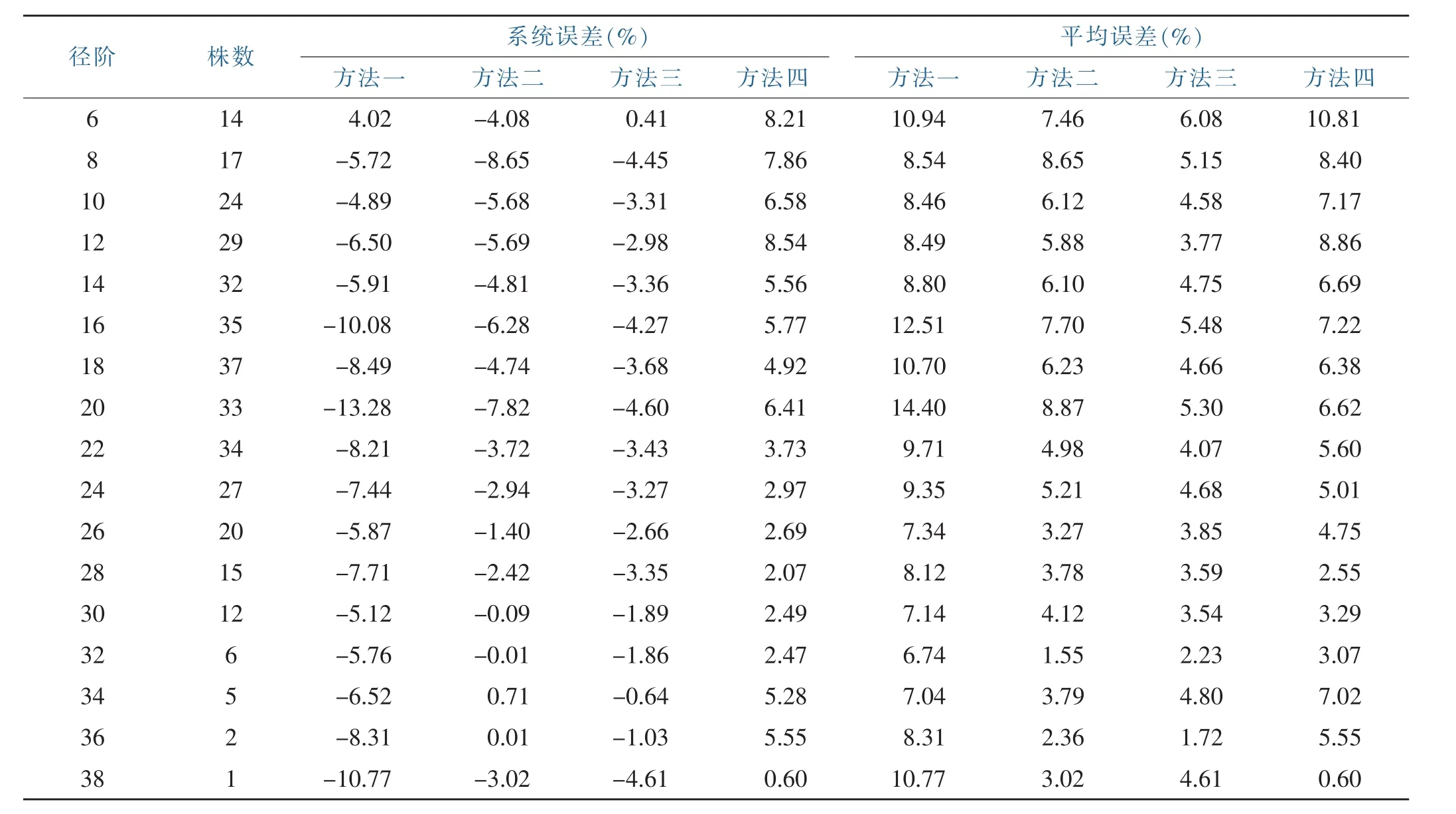
表2 各径阶误差平均值Table 2 Mean value of each order error

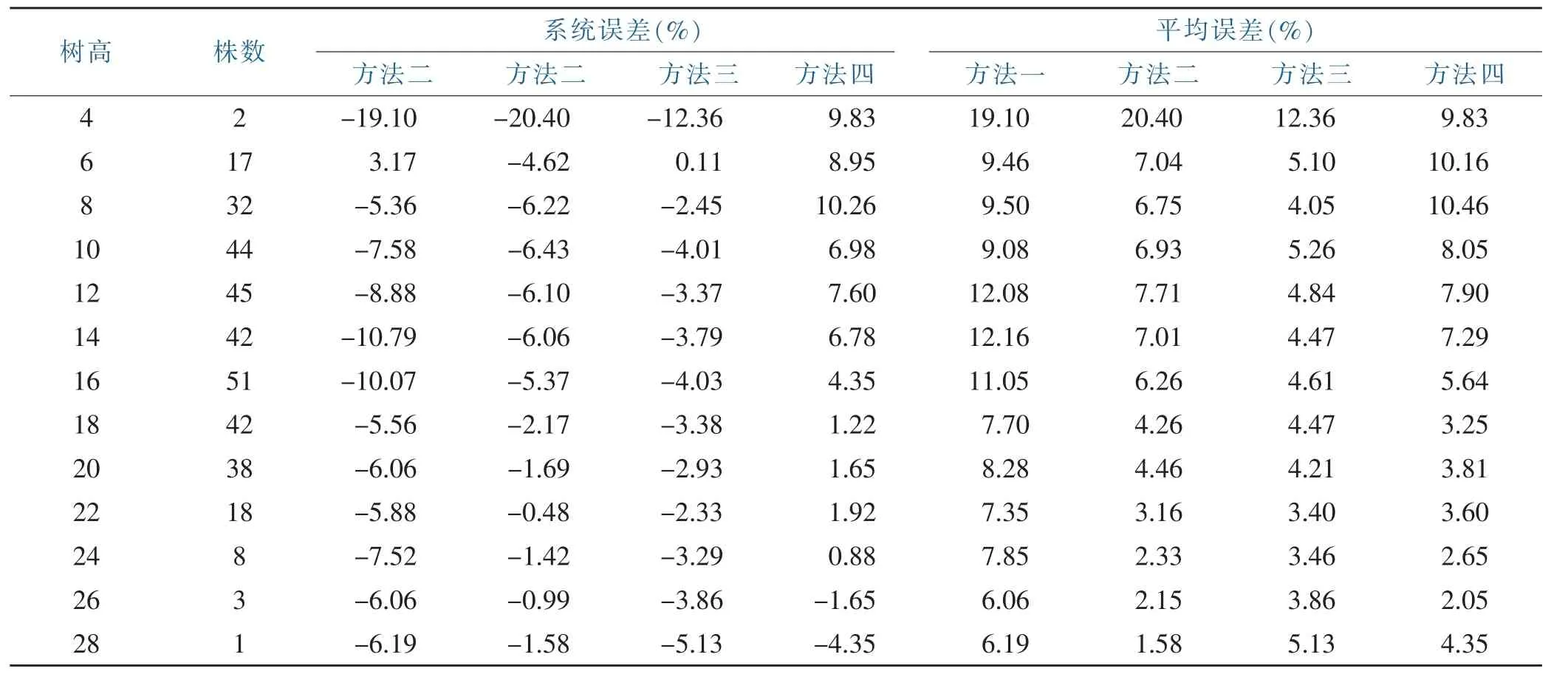
表3 各树高级误差平均值Table 3 High error average of each tree

方法一各树高级的系统误差多数大于其他三种方法，除树高级6 m外，系统误差都超过5%。当树高大于16 m时，方法二和方法四的系统误差均小于正负3%，方法三的各树高级材积测定误差差别不大，基本上都小于5%，个别树高级例外，如最小树高级4米和最大树高级28 m，但这二个树高级株数太少，难以说明实际问题。方法四的系统误差除了树高级26 m和28 m外，其他各树高级均为正值，表明材积测定值整体上大于实际材积。其他三种方法则相反，各树高级的系统误差基本上都为负值，表明材积测定值偏小。

从平均误差来看，方法一各树高级误差大于其他三种方法，均在5%以上，方法二和方法四基本上差不多。树高小于18 m时，方法三各树高级的误差明显小于其他三种方法。当树高大于18 m时，方法二、方法三和方法四各树高级的误差比较接近，以方法三略大一些，但误差均小于5%。

各树高级误差分布情况除方法四外，其他三种方法均在树高4 m时误差最大，但树高4 m与树高6,8 m的误差差别不明显，由于树高级4 m只有2株树，其结果还不能充分说明问题。

2.4 材积测定方法的改进

上述分析表明，用方法三测定材积存在系统性偏小的问题，而方法四则相反，呈系统性偏大。基于此，将这二种方法的测定结果取平均值，得到改进的材积测定方法五。公式如下。

式中：V5为改进后的材积测定值；V3为方法三的材积测定值；V4方法四的材积测定值。

用样木材料计算方法五的材积测定误差，结果为：负误差次数百分数为44.9%，最大负误差为-8.78%，正误差次数百分数为55.14%，最大正误差21.5%，正负误差次数相差不是很大，以正误差所占比例居多，最大正误差的数值也大于最大负误差。从误差大小来看，正负误差在5%范围内所占比例为77.26%，正负误差在范围内10%所占比例为96.79%，即材积测定误差超过10%的样木所占比例不足5%。系统误差0.98%，小于3%且接近于零，基本可认为不存在明显的趋势性系统偏差。平均误差3.37%，小于5%。显然，改进后方法五的材积测定各项误差指标优于前述的四种方法，明显提高了材积的测定精度，在森林资源调查中有推广应用价值。

3 小结

应用形数等于形率平方、形数等于形率减去一个常数、希费尔公式、书斯托夫式等4个形数与形率的关系式推算形数，并测定单木材积，以希费尔公式精度最高，形数等于形率平方关系式精度最低。从误差方向来看，书斯托夫式测定结果大多数大于实际材积，其他3个公式则相反，大多数小于实际材积。

将希费尔公式、书斯托夫式测定结果取平均后作为单木材积的测定值，明显消除了材积测定的系统偏大或偏小的误差，提高了材积测定精度，在立木材积测定中有推广应用价值。