基于随机模拟的地下水污染物最优水力截获量
2018-09-25付晓刚唐仲华吕文斌王小明闫佰忠
付晓刚,唐仲华,吕文斌,王小明,闫佰忠
基于随机模拟的地下水污染物最优水力截获量
付晓刚1,2*,唐仲华1,吕文斌3,王小明2,闫佰忠2
(1.中国地质大学环境学院,湖北 武汉 430074;2.河北地质大学,河北省水资源可持续利用与开发重点实验室,河北省水资源可持续利用与产业结构优化协同创新中心,河北 石家庄 050031;3.河北省地矿局第三水文工程地质大队,河北 衡水 053000)
水力截获技术是净化或抑制地下水污染最为广泛使用的一种方法,而该技术实施过程中,如何确定最优水力截获量是其需要重点解决的关键问题.本文针对传统确定性方法计算最优水力截获量不合理的问题,从水文地质参数的随机性出发,应用基于随机理论的蒙特卡罗方法,通过实例来研究渗透系数的空间变异性对地下水污染物水力截获系统的影响,并寻求估算最优水力截获量的新方法.通过研究表明:基于确定性方法计算出最优水力截获量为110m3/d时恰好能完全截获污染区的污染物;应用随机模拟研究含水层渗透系数的空间变异性对水力截获系统的影响,发现当以传统确定性方法所计算的最优水力截获量(110m3/d)抽水时,并不能总是完全截获地下水污染物,其面临的稳定平均风险率高达24%;充分考虑了含水层渗透系数空间变异的Monte Carlo方法较以往传统确定性方法更为可靠,为此本文提出利用随机方法从截获系统可接受风险角度确定最优截获量的新思路.
随机模拟;蒙特卡罗模拟方法;空间变异性;水力截获
地下水是我国城市,特别是北方城市的重要供水水源,随着工农业的发展,其污染问题已甚为严重,引起了广泛关注。在被污染含水层的治理过程中,人们往往根据污染物的种类、污染特征及含水层背景条件而分别采用不同的方法,目前在实际工程中应用较广的主要有水力截获法、原位生物处理法、原位化学氧化法、自然衰减法和渗透性反应墙[1-2].其中,水力截获法简单易行,可对地下水污染事件做出快速反应,是消除地下水污染和控制污染羽扩散的修复技术中使用率最高的一种.该方法是通过设置一系列合理的抽水井人工改变地下水天然流动方式制造人工流场,最大限度地汇集和抽取受污染地下水以达到修复受污染的含水层并抑制污染羽扩散的一种水动力学技术[1,3].水力截获技术的核心是设计一种有效的截获系统恰当地截取被污染的地下水而不允许污染物运移到下游去[1,4].在该技术实施过程中,抽水量的大小在很大程度上决定了修复工程的有效性及经济性[5],因此如何确定抽水井的最优水力截获量是需要重点解决的问题.
目前国内外主要通过模拟-优化模型来对水力截获系统的最优截获量进行确定[5-8],以寻求最小的经济投入满足既定的修复目标[2].通常模拟-优化模型由地下水流及溶质运移数值模型和最优化模型耦合而成,而以往研究对数值模拟和溶质运移数值模型中含水层参数的选取均是确定的,而实际上,由于含水层岩性和地质构造固有的复杂性,及受经济技术条件限制造成水文地质参数获取的局限性,以至于研究者无法完全真实地刻画含水层的水文地质信息,这就导致计算结果往往带有一定的不确定性。为表达由含水层系统的非均质性引起的结果不确定性,Dagan等最早提出并发展了随机理论的研究方法[9-15].目前将基于不确定性的随机方法多用于地下水资源评价方面,如曾将随机模拟与风险评估相结合,用于地下水允许开采量的确定[16-17],而结合随机方法研究最优水力截获量的并不多见.
鉴于渗透系数在很小的区域内可以变化几个数量级[18-19],与渗透系数相比,孔隙率、给水度及其它水文地质参数的空间变化幅度相对较小,因此,本文应用基于随机理论的蒙特卡罗方法研究渗透系数的空间变异性对水力截获系统的影响,并从可接受风险角度寻求确定最优水力截获量的新思路.
1 研究方法
1.1 渗透系数随机分布的生成
众多研究结果表明, 渗透系数的空间变异性是影响含水层中地下水运动的决定性因素[20-21],渗透系数随机分布场的产生是否合理,直接影响到随后的数值计算成果是否符合实际.
Freeze[22]通过统计大量含水层渗透系数和孔隙度的空间变化特征,认为含水层渗透系数的空间变化规律可以用对数正态分布来表述,这一结果被后来的大量研究进一步证实并得到了广泛地应用[23-27].许多学者基于这一统计规律,推导出了渗透系数随机场的计算方法和电算程序[28-30],此次采用Taskinen提出的方法来生成渗透系数的随机场[31],计算公式如下:

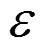
1.2 蒙特卡罗方法
蒙特卡罗方法是基于计算机模拟的统计试验方法,它适用性广,方法简单,能将模型参数的不确定性转化为模拟结果的不确定性[32-35].该方法假定随机变量(如渗透系数)的概率分布函数以及随机变量之间的相关结构都是已知的,利用随机数生成足够多组服从给定分布规律的随机变量,然后对每组随机变量分别运行数值模型,再用统计的方法评价这些随机变量所对应的模拟结果即可获得模拟结果的不确定性.
本文采用蒙特卡罗方法评价渗透系数的空间变异性对水力截获系统最优截获量的影响,大致步骤如下:
(1)利用蒙特卡罗方法由Taskinen提出的公式生成100组符合给定分布特征的渗透系数场.
(2)对每个生成的渗透系数场,分别运行对应条件下的水流模型,以获得相应的地下水流场及速度场.
(3)分别运用MODPATH对截获系统抽水井进行粒子反向追踪,进而分别确定出所对应的水力截获风险率(即截获带未涵盖的污染区与整个污染区的面积百分比).
(4)最后统计出渗透系数随空间变异情况下,水力截获系统平均风险率.
以上步骤中第一个步骤是本次研究的重点,因为渗透系数场产生的合理与否,直接关系到随后的结果是否符合实际.

图1 蒙特卡罗方法确定水力截获系统平均风险率流程
2 实例分析
2.1 算例概况
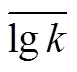

图2 研究算例平面图及有限差分剖分网格
以上理想模型的最优水力截获量可通过解析方法来计算,但考虑到本文主要讨论渗透系数在空间上的变异对水力截获系统的影响,因此,无法用解析法求解,只有通过数值模拟方法才能实现这一目标.
2.2 地下水流模型
根据研究区水文地质条件,即可建立研究区内地下水稳定流数学模型:
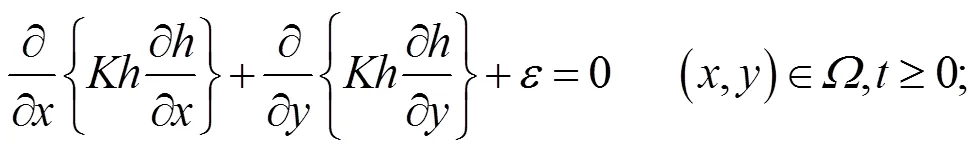

式中:为研究区范围;为地下水水位,m;为含水层的渗透系数,m/d;为含水层的源汇项,m/d;Γ2,4为研究区南部和北部的零流量边界;Γ1,3为研究区西部和东部的定水头边界,m;为Γ2,4边界的外法线方向.
2.3 粒子运移数学模型
美国地质调查局开发的MODPATH是专门用于水质点示踪模拟研究的程序,在本次研究中采用对水力截获井向后示踪方法,来确定抽水井的截获范围.
MODPATH中采用线性速度插值方案,使用直接积分方法来确定一个格网内粒子的二维运动,在t时刻的粒子位置用下式确定[36]:
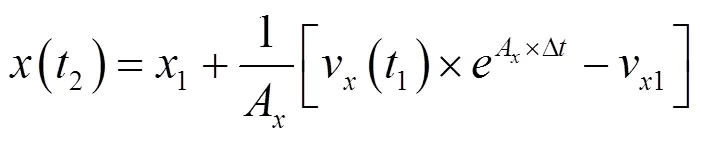
其中:


2.4 模拟结果分析与讨论
研究区被离散为60行60列的矩形网格,使用有限差分法求解地下水水流模型,得到地下水流场及速度场,然后在其基础上使用MODPATH软件对截获系统抽水井进行粒子反向追踪,最终得到截获带范围.

图3 均质条件下截获井以最优水力截获量110m3/d开采时的截获范围
为了与传统确定性参数模型得到的最优水力截获量结果相比较,首先采用确定性模型(整个研究区的渗透系数取值为不确定性输入参数的均值lg= 1.48,即不考虑渗透系数空间变异的影响)进行了水力截获井的最优截获量求解,确定出当截获量为110m3/d时,恰好能完全截获污染区的污染物.为便于对比,图3中绘制出了确定模型均质条件下(lg=1.48)以最优截获量抽水时的污染物截获范围图.
为对比研究渗透系数的随机特征对水力截获系统的影响,笔者使用蒙特卡罗方法由Taskinen提出的公式生成了100组符合给定分布特征的渗透系数场(lg的均值和方差分别为1.48和0.5,相关长度为60m).
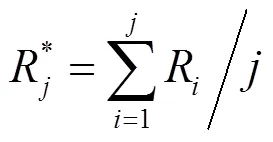
由截获系统平均风险率(R*)序列图(图6)可以看出,当模拟次数达到20次时,平均风险率为28%,当模拟次数增加到50次时,平均风险率为22%,随着模拟次数的增加,平均风险率呈现逐渐收敛特征,当模拟次数接近100次时,平均风险率变化幅度已非常小,达到较好地收敛,为24%.

图4
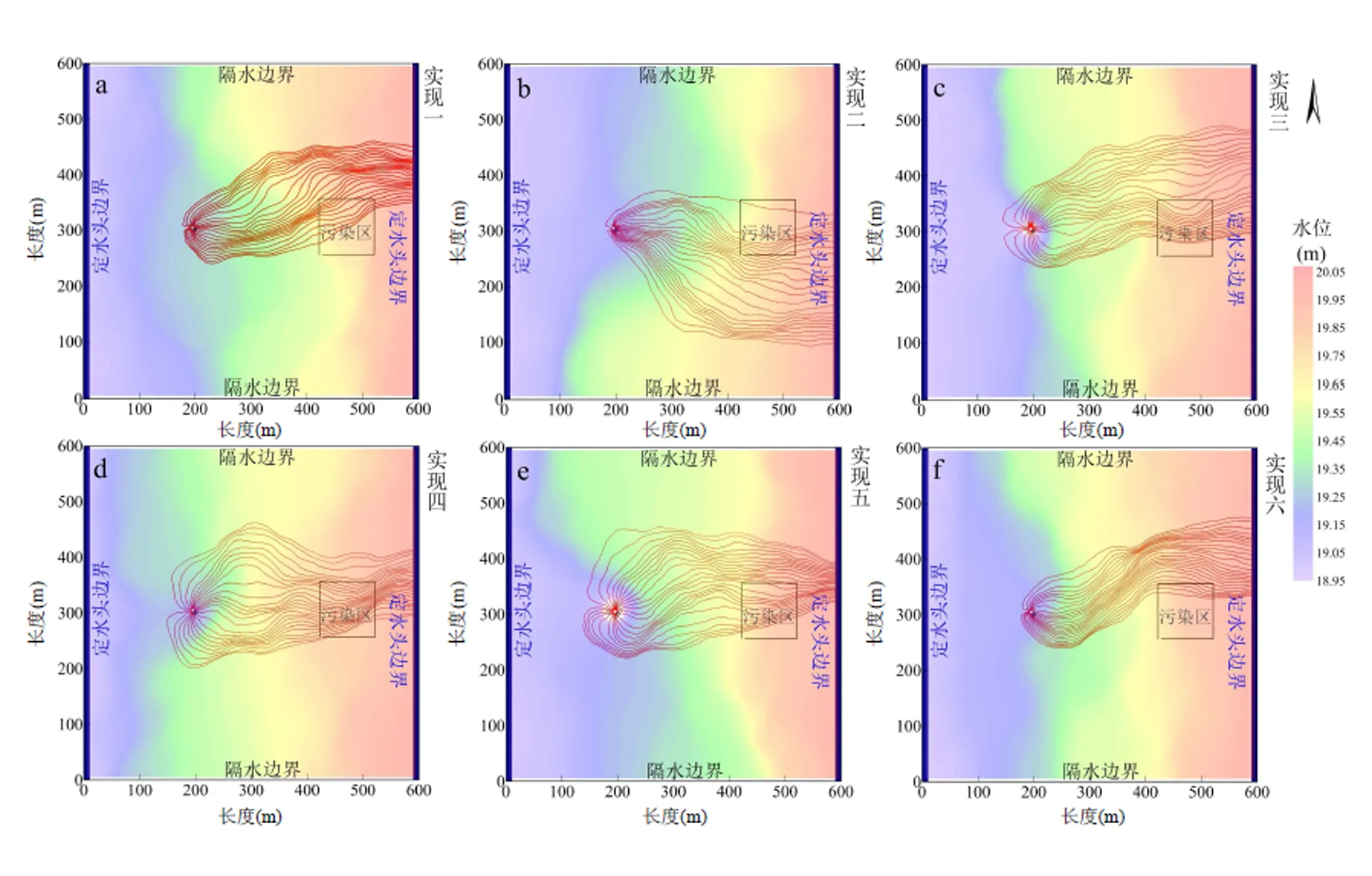
图5 与不同渗透系数随机场所对应的污染物水力截获范围图(组次1~6)
6组模拟结果风险率(R)大小分别为:50%、15%、27%、14%、26%和79%,平均风险率(R)则分别为50%、33%、31%、27%、27%和35%
通过以上对比分析,说明采用传统确定性方法(研究区渗透系数取平均值)来估算水力截获系统最优截获量,是不太合理的,其结果平均风险率高达24%,因此生产实践中不可直接采用传统确定参数方法所计算的最优截获量,因为这样做掩盖了不能完全截获污染物而造成地下水污染的风险.
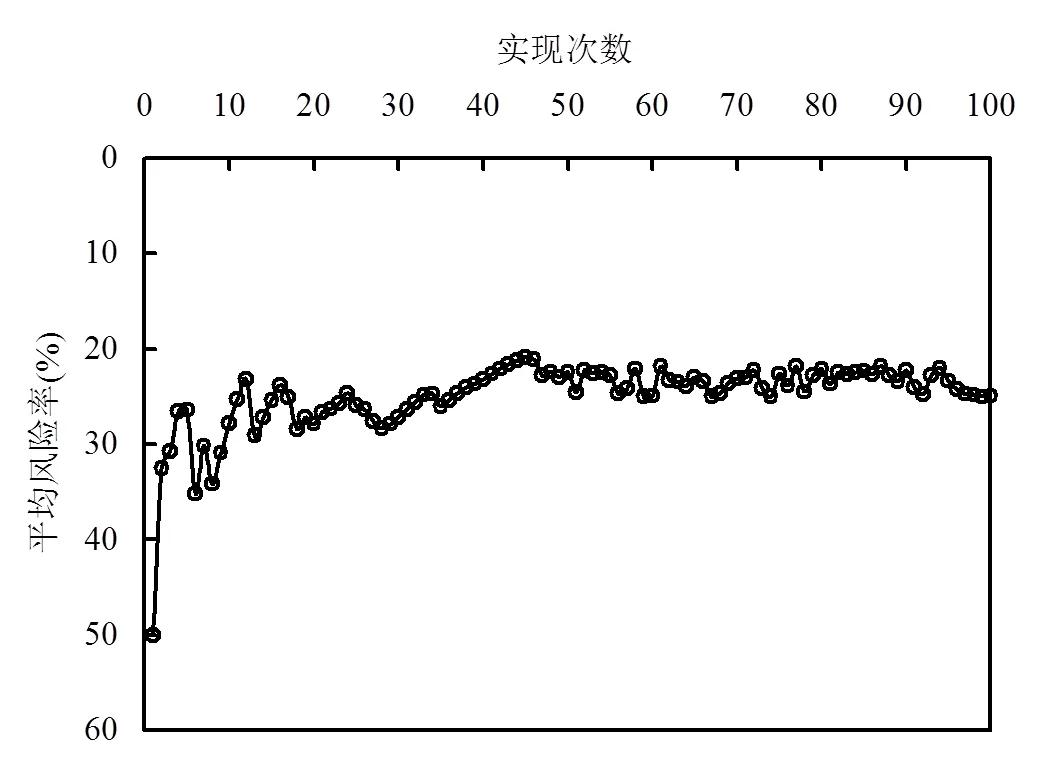
图6 渗透系数不同实现次数所对应的污染物水力截获平均风险率(截获井抽水量为110m3/d)
本次研究的方法可为今后地下水污染修复工作中,更加合理、可靠地确定水力截获系统的最优截获量提供一种切实可行的新思路,按照文中方法可定量评价不同截获量所面临的风险率大小,能有效弥补传统的确定性参数模型估算最优水力截获量的不足,使管理者可从风险损失出发对截获系统最优截获量进行合理确定.
本研究成果可以有效地分析和评估水力截获系统的风险,有助于管理者对风险的把握和掌控,故研究渗透系数的不确定性对水力截获系统结果的影响对于地下水污染修复和风险预警都具有重要的作用.
3 基于稳定平均风险率的最优截获量确定
为量化水力截获量大小与风险率之间的关系,此次研究使用数值模拟方法对前述算例中截获井又分别设定了80,90,100,120,130,140,160m3/d共7组抽水量(见表1),并分别模拟计算了lg的100次实现所对应污染物截获范围,最终测量统计得到不同截获量所对应的污染物水力截获平均风险率分布序列(如图7所示).由图7可以看出,随着模拟次数的增加,平均风险率均呈现逐渐收敛特征,最终稳定后的平均风险率分别为:41%、35%、29%、19%、15%、12%、8%(见表1).

图7 不同截获量所对应的污染物水力截获平均风险率

表1 不同截获量所对应的稳定平均风险率
不同截获量所对应的稳定平均风险率可视为水力截获系统在取不同水力截获量时所面对的相对风险.由图8可见,不同水力截获量与相应的稳定平均风险率之间满足指数关系(可决系数0.98),截获系统水力截获量选择得越大,由渗透系数空间变异性所带来的截获系统未能完全截获污染物的风险越小,但抽出的水中则可能包含了没有受到污染的洁净水,以致地面污水处理费用增加;截获系统抽水量选择得越小,不能完全截获污染物的风险则越大,污染物可能会流到截获井的下游,污染地下水环境.
由于不同污染物的毒性和降解能力不同,因此截获系统可接受的稳定平均风险率可通过包含污染物毒性参数和降解能力在内的健康风险损害模型来确定,其具体确定方法不在本次研究的范围之内,可参考文献[37]等相关研究成果.在实际工作中应根据经济合理性和可接受的风险大小对截获系统的最优截获量进行综合考虑,以便从风险损失出发进行合理确定.
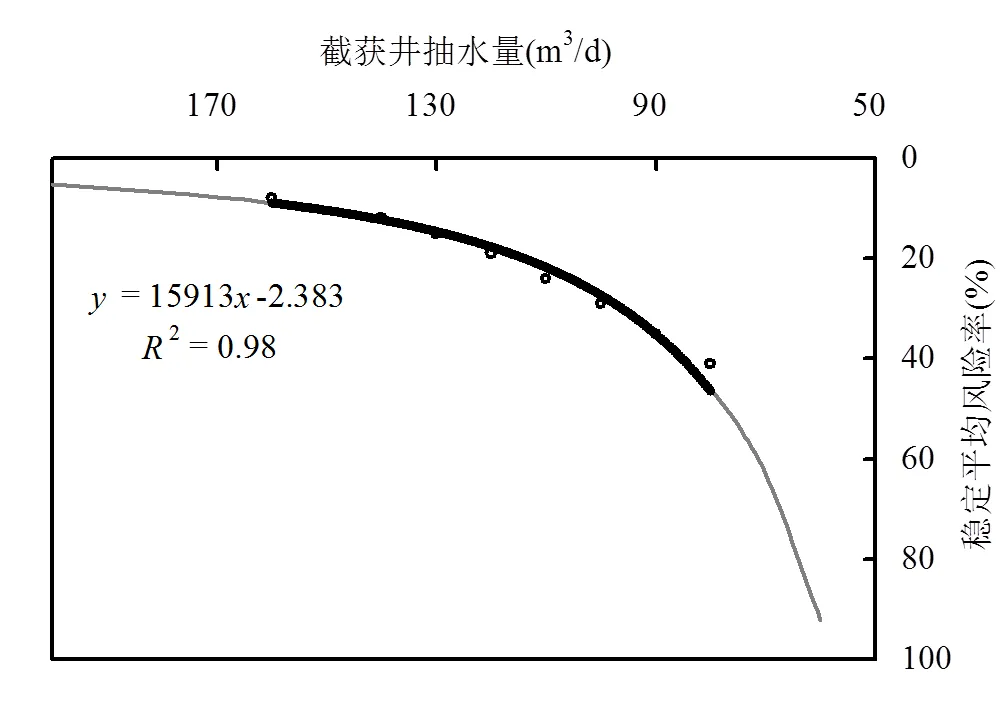
图8 截获量与稳定平均风险率回归关系
值得注意的是对于粘滞性较高或者吸附性较强的污染物,由于其通过含水层比水通过含水层要慢得多,因此将会减缓污染物自含水层中的去除,从而造成水力截获系统抽水耗时长,运行维护总费用高,去除效率不理想,以及严重的反弹效应等问题.因此,对于这种情况,建议在采用水力截获技术控制污染的扩散和降低污染物浓度后,配合原位修复或自然衰减法等方法,进一步使污染浓度达标.
4 结论
4.1 含水层的渗透系数具有很强的空间变异性,因此利用传统方法(研究区渗透系数取平均值)计算出的最优水力截获量往往不可靠.通过文中实例可知,传统确定性方法所估算的截获系统最优抽水量,稳定平均风险率高达24%,并不能完全截获污染物,因此,最优水力截获量的确定必须依靠随机性模型来确定,或者至少应在确定性模型中引入随机参数.
4.2 不同水力截获量与相应的稳定平均风险率之间满足指数关系,截获系统抽水量选择得越大,由渗透系数空间变异性所带来的截获系统未能完全截获污染物的风险越小.不同截获量所对应的稳定平均风险率可视为确定截获系统抽水量时所面临的相对风险值,实际工作中应根据经济合理性和可接受的风险大小从关系曲线上选取合适的截获量,以便从风险损失角度出发对截获系统最优截获量进行合理确定.
[1] 顾 栩,杜 鹏,单慧媚,等.水力截获技术在地下水污染修复中的应用—以某危险废物填埋场为例[J]. 安全与环境工程, 2014,21(4): 52-58.
[2] Kiecak A, Malina G, Kret E, et al. Applying numerical modeli-ng for designing strategies of effective groundwater remedi-ation [J]. Environmental Earth Sciences, 2017,76(6):248-261.
[3] 任增平.水力截获技术及其研究进展[J]. 水文地质工程地质, 2001, 28(6):73-77.
[4] Truex M, Johnson C, Macbeth T, et al. Performance assessment of pump-and-treat systems [J]. Groundwater Monitoring & Remediation, 2017,37(3):28-44.
[5] 万 鹏,张 旭,李广贺,等.基于模拟-优化模型的某场地污染地下水抽水方案设计[J]. 环境科学研究, 2016,29(11):1609-1615.
[6] 郇 环,王金生.水力截获技术研究进展[J]. 环境污染与防治, 2011,33(3):83-87.
[7] Yang Y, Wu J, Wang J, et al. An elitist multiobjective tabu search for optimal design of groundwater remediation systems. [J]. Ground Water, 2017,55(6):811-826.
[8] Majumder P, Eldho T I. A new groundwater management model by coupling analytic element method and reverse particle tracking with cat swarm optimization [J]. Water Resources Management, 2016,30(6): 1953-1972.
[9] Dagan G. Stochastic modeling of groundwater flow by unconditional and conditional probabilities:1:conditional simulation and the direct problem [J]. Water Resources Research, 1982,18(4):813-833.
[10] Dagan G. Flow and transport in porous formations [M]. New York: Springer-Verlag, 1989:18-24.
[11] 杨金忠,蔡树英,叶自桐.区域地下水溶质运移随机理论的研究与进展[J]. 水科学进展, 1998,9(1):85-97.
[12] Zhang D, Andricevic R, Sun A Y, et al. Solute flux approach to transport through spatially nonstationary flow in porous media [J]. Water Resources Research, 2000,36(8):2107-2120.
[13] 姚磊华,罗焕炎,张茂省.白杨水源地潜水水质的Monto-Carlo随机模拟[J]. 吉林大学学报:地球科学版, 1998,28(3):296-302.
[14] 束龙仓,李 伟.北塘水库库底地层渗透系数的随机特性分析[J]. 吉林大学学报:地球科学版, 2007,37(2):216-220.
[15] 刘佩贵,束龙仓.傍河水源地地下水水流数值模拟的不确定性[J]. 吉林大学学报:地球科学版, 2008,38(4):639-643.
[16] 束龙仓,朱元生,孙庆义,等.地下水允许开采量确定的风险分析[J]. 水利学报, 2000,31(3):77-81.
[17] 李如忠,汪家权,钱家忠.地下水允许开采量的未确知风险分析[J]. 水利学报, 2004,35(4):54-60.
[18] Feyen L, Jr P J R, Smedt F D, et al. Stochastic delineation of capture zones: classical versus Bayesian approach [J]. Journal of Hydrology, 2003,281(4):313-324.
[19] 梁 婕.基于不确定理论的地下水溶质运移及污染风险研究[D]. 长沙:湖南大学, 2009:28.
[20] 杨金忠,蔡树英,伍靖伟.宏观水力传导度及弥散度的确定方法[J]. 水科学进展, 2002,13(2):179-183.
[21] 陆 乐,吴吉春,王晶晶.多尺度非均质多孔介质中溶质运移的蒙特卡罗模拟[J]. 水科学进展, 2008,19(3):333-337.
[22] Freeze R A.A stochastic-conceptual analysis of one-dime-nsional groundwater flow in nonuniform homogeneous media [J]. Water Resources Research, 1975,11(5):725-741.
[23] 李 伟,束龙仓.湖区地层垂向渗透系数概率分布特征分析[J]. 水利水电科技进展, 2005,25(2):20-22.
[24] 施小清,吴吉春,袁永生.渗透系数空间变异性研究[J]. 水科学进展, 2005,16(2):210-215.
[25] Guo Z, Brusseau M L. The impact of well-field configuration and permeability heterogeneity on contaminant mass removal and plume persistence [J]. Journal of Hazardous Materials, 2017,333:109-115.
[26] Pedretti D, Masetti M, Beretta G P. Stochastic analysis of the efficiency of coupled hydraulic-physical barriers to con-tain solute plumes in highly heterogeneous aquifers [J]. Journal of Hydrology, 2017,553:805-815.
[27] 王 超,束龙仓,鲁程鹏.渗透系数空间变异性对低渗透地层中地下水溶质运移的影响[J]. 河海大学学报(自然科学版), 2014,42(2): 137-142.
[28] Cho S E. Probabilistic stability analysis of rainfall-induced landslides considering spatial variability of permeability [J]. Engineering Geology, 2014,171(8):11-20.
[29] Yang Y, Wu J, Luo Q, et al. Effects of Stochastic Simulationson Multiobjective Optimization of Groundwater RemediationDesign under Uncertainty [J]. Journal of Hydrologic Engineering, 2017,22(8): 1-12.
[30] Taskinen A, Sirviö H, Bruen M. Generation of two-dimensi-onally variable saturated hydraulic conductivity fields: Modeltheory, verification and computer program [J]. Computers & Geosciences, 2008,34(8):876-890.
[31] 张 博,李国秀,程 品,等.基于随机理论的地下水环境风险评价[J]. 水科学进展, 2016,27(1):100-106.
[32] 欧阳琦,卢文喜,侯泽宇,等.基于替代模型的地下水溶质运移不确定性分析[J]. 中国环境科学, 2016,36(4):1119-1124.
[33] 陆 乐,吴吉春.地下水数值模拟不确定性的贝叶斯分析[J]. 水利学报, 2010,41(3):264-271.
[34] 李久辉,卢文喜,常振波,等.基于不确定性分析的地下水污染超标风险预警[J]. 中国环境科学, 2017,37(6):2270-2277.
[35] 徐 亚,朱雪梅,刘玉强,等.基于随机-模糊耦合的污染场地健康风险评价及案例[J]. 中国环境科学, 2014,34(10):2692-2700.
[36] Chiang W H. 3d-groundwater modeling with pmwin: A simulation system for modeling groundwater flow and transport processes [M]. New York: Springer-Verlag, 2005.
[37] Qu M, Li W, Zhang C. Assessing the risk costs in delineating soil nickel contamination using sequential Gaussian simulation and transfer functions [J]. Ecological Informatics, 2013,13(13):99-105.
Optimal pumpage to purify contaminative groundwater based on stochastic simulation.
FU Xiao-gang1,2*, TANG Zhong-hua1, LÜ Wen-bin3, WANG Xiao-ming2,YAN Bai-zhong2
(1.School of Environmental Studies, China University of Geoscience, Wuhan 430074, China;2.Key Laboratory of Sustained Development and Utilization of Water Resources, Hebei Province Collaborative Innovation Center for Sustainable Utilization of Water Resources and Optimization of Industrial Structure, Hebei GEO University, Shijiazhuang 050031, China;3.Third Hydrogeological Engineering Team of Hebei Provincial Geological and Mining Burea, Hengshui 053000, China)., 2018,38(9):3421~3428
Hydraulic capture technique is one of the most widely applied technologies to purify orconstrain contaminants from further contaminatedgroundwater. Thus, how to determine the optimal pumpage is the key issue.The optimal pumpage calculated by commonly used deterministic methodswere usually unreasonable.Therefore, the Monte Carlo method based on the stochastic theory, in consideration of the stochastic property of hydrologic-geologic parameters, was applied to investigate the effect of the spatial variation of hydraulic conductivity on the fate of hydraulic capture zone and a new method to estimate the optimal pumpage was suggested. It had been proved that when the 110m3/d determined by means of deterministic methods was adopted as optimal pumpage, the contaminated area lay exactly within the capture zone of the well, Then, stochastic method was used to investigate the effect of spatial variation of hydraulic conductivity on hydraulic capture zone and the results indicated that the capture zone did not always cover the entire contaminated area when the optimal pumpage adopted the same value (110m3/d) according to traditional deterministic methods, facing a convergent mean risk criterion as high as 24%. This study showed that the optimal pumpage concluded from the Monte Carlo method was more reliable than commonly used deterministic method, because it could takes such spatial variation of hydraulic conductivity into account to study how the spatial variability effected the hydraulic capture zone, that provided a stochastic method to estimate the optimal pumpage from the perspective of acceptable convergent mean risk criterion.
stochastic modeling;Monte Carlo simulation method;spatial variation;hydraulic capture
X523
A
1000-6923(2018)09-3421-08
付晓刚(1983-),男,陕西西安人,讲师,博士,主要从事地下水流数值模拟研究.发表论文10余篇.
2018-01-03
河北省高等学校科学技术研究项目(QN2015061);河北省自然科学基金资助项目(D2018403040);中国博士后基金面上项目(2018M631874);河北省水利科技计划项目(2017-59)
* 责任作者, 讲师, fuxiaogang007@163.com
