旋转式多臂机提综机构动力学分析与优化

金国光， 魏晓勇， 魏 展， 畅博彦， 张旭阳

(1. 天津工业大学 机械工程学院， 天津 300387； 2. 天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387)

旋转式多臂机是目前最先进的高速开口装置[1,2]，其作用是按照一定的规律将经丝分为上下两层，形成可经过纬线的通道—梭口，以供纬线从中穿过，具有工作稳定、结构紧凑、运动精度高、控制简单等优点，一般用于制造有小花纹的织物，普遍应用于剑杆织机、喷气织机等无梭织机中。

旋转式多臂机由提综机构、选综机构、电控设备等部分构成。提综机构是旋转式多臂机最核心的部分，其将电机输入的匀速圆周运动转化为综框在竖直方向的上下运动，保证织机的正常运行。所以，研究旋转式多臂机提综机构对提升织机的整体性能有重要意义。

目前，对旋转式多臂机提综机构的研究主要集中于2个方面：一是对机构进行运动学分析；二是运用虚拟软件对机构进行动态建模获得其动态性能指标。沈毅等[3-5]对旋转式多臂机提综机构的运动机理进行了分析，并对主传动机构进行了三维建模，运用矢量三角形法对主传动机构进行了运动学求解，采用等效简化模型的方法对机构进行了动力学分析，设计了多臂机的测试系统。季海彬等[6]对多臂机提综机构进行了参数特征和载荷研究，分析了提综机构中各个构件在主轴上的等效转动惯量，分析占比规律。EREN等[7]对旋转式多臂机运动学进行分析，重点讨论了机构参数对综框运动规律的影响。

以上研究为旋转式多臂机提综机构的运动特性分析和动力学建模奠定了一定基础。然而，随着人们对生产率的不断追求，现代织机转速越来越高，高速化带来的机器振动、稳定性降低、寿命缩短等问题亟待解决，旋转式多臂机提综机构作为织机开口机构的关键部分，深入研究其动力学性能对解决此类问题具有重要意义。运用虚拟软件进行动力学研究步骤繁琐、优化难度大，所以，精确建立旋转式多臂机提综机构动力学模型[8-10]是研究该机构的动力学性能[11]、提高工作质量和工作效率的基础和关键。

为此，本文首先建立旋转式多臂机提综机构的运动学模型，并以此为基础应用Lagrange方程建立机构的动力学模型，运用MatLab软件对动力学模型进行数值仿真计算，并用ADAMS软件建立系统虚拟样机，通过对比二者所得大圆盘驱动力矩的一致性，验证所建动力学模型的正确性，在此基础上对系统的动力学特性进行优化，为旋转式多臂机整体性能的改善提供理论依据与指导。

1 旋转式多臂机提综机构工作原理

旋转式多臂机通常包括16个提综臂，每个提综臂对应控制1个综框运动，在实际工况下，综框的数目以及运动规律随织机织布纹理的要求而变化，提综机构一般带动偶数片综框，可以将其分为2组，每组运动规律相似，在保证模型有效的前提下，为节约计算资源，假设旋转式多臂机选综系统作用结果为2个提综臂带动2个综框以180°的相位差持续运动，在此工作状态下对机构进行分析。

图1示出旋转式多臂机提综机构的工作原理简图。为了机构平衡，减小冲击，在圆盘上成180°对称安装2个凸轮摆臂，图中省略了其中1个凸轮摆臂和与其配合的凸轮滚子以及滑块等构件。构件8～15相互串联驱动综框16运动，另外1个综框以及连杆的连接情况与其完全相同，故图1省略了另外1个综框25以及对应的连杆构件。

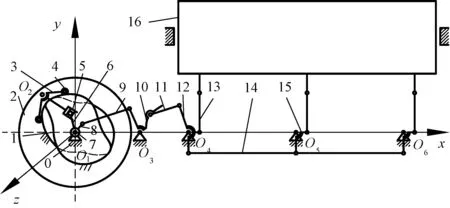
0—多臂机箱体； 1—共轭凸轮； 2—大圆盘；3—凸轮摆臂； 4—凸轮滚子； 5—滑块； 6—滑块架；7—旋转轴； 8—偏心盘； 9—环形连杆； 10—提综臂；11—提综连杆； 12—大刀片； 13—转臂连杆；14—综框连杆； 15—小刀片； 16—综框。

旋转式多臂机提综机构由共轭凸轮旋转变速机构和平面连杆机构组成，综框平面连杆机构包括2个串联的平面四连杆机构及综框连杆机构，见图1。

共轭凸轮1、大圆盘2、凸轮摆臂3、凸轮滚子4、滑块5、滑块架6、旋转轴7组成旋转变速机构，将大圆盘2匀速圆周旋转转化为旋转轴7的非匀速圆周运动是其最本质特征。共轭凸轮1固定在多臂机箱体0上，外部输入电动机经过传动比为2∶1的齿轮传动带动大圆盘2匀速圆周运动。铰接在大圆盘2上的凸轮摆臂3随着大圆盘转动的同时又沿着凸轮摆动，凸轮摆臂3带动滑块5绕大圆盘旋转中心转动，同时又在摆臂3滑槽中滑动。滑块5和滑块架6铰接在一起，滑块架6在滑块5的带动下绕大圆盘旋转轴线作非匀速的圆周运动，旋转轴7和滑块架6固连，且和偏心盘8之间通过花键连接，偏心盘8绕大圆盘旋转轴线旋转。

偏心盘8、环形连杆9、提综臂10组成曲柄摇杆机构，偏心盘8圆周运动带动提综臂10往复摆动。提综臂10、提综连杆11、大刀片12组成双摇杆机构，提综臂10的往复摆动带动大刀片12绕旋转中心作一定角度的旋转运动。由于综框宽度大，为增大系统刚度，用2组综框连杆14及小刀片15来传递动力。大刀片及小刀片带动转臂连杆13作平面运动，综框16由3个平行的转臂连杆13推动上下运动。

2 提综机构运动学建模

由图1可知，在大圆盘中心建立固定坐标系O1XYZ,z轴方向过坐标原点且垂直平面向外。根据旋转式多臂机提综机构的工作原理，将其分为旋转变速机构和平面连杆机构2部分进行运动学分析。

2.1 旋转变速机构

图2示出旋转变速机构简图。旋转变速机构中核心部件为共轭凸轮及凸轮摆臂，为保证输出旋转轴7运动无冲击，要求其角速度及角加速度连续，共轭凸轮廓线采用摆线修正等速运动规律曲线。假设初始时刻滑块架O1B处于竖直位置，凸轮摆臂上滑槽中心线O2B也为竖直位置，φ为大圆盘旋转角度，α为滑块架旋转角度，即多臂机旋转轴7的旋转角度，也代表偏心盘的旋转角度，结合运动规律，规定α和φ顺时针方向为正。综合考虑整个开口工艺过程，设定大圆盘旋转角度在[0°,180°)和[180°,360°)时，旋转轴7的运动规律完全相同，且大圆盘旋转角度在[0°,15.5°)和[180°,195.5°)时，旋转轴7静止。α随φ在各个区段的变化规律如下。

图2 旋转变速机构运动分析图Fig.2 Kinematic diagram of rotating mechanism with variable velocity

1) 静止区段：

α=0°

(1)

此时φ∈[0°,15.5°)。

2) 摆线运动加速区段：

(2)

式中φ∈[15.5°,45.5°)。

3) 等速运动区段：

(3)

式中φ∈[45.5°,150°)。

4) 摆线运动减速区段：

(4)

式中φ∈[150°,180°]。

各构件的方位角θ均应由x轴开始，规定沿逆时针方向计量为正。图2中θ1为凸轮摆臂上O2B与x轴正方向夹角，即滑块5与x轴正方向夹角，根据几何关系可求得

(5)

(6)

式中ψ为O2B相对大圆盘O1O2旋转的角度，选定逆时针方向为正，ψ∈(-π/2,π/2)。

2.2 平面连杆机构

2个综框及连杆机构都由旋转变速机构中旋转轴7驱动，在选综系统的作用下，2个综框对应的偏心盘运动规律差异造成2个综框相向运动且相位相差180°。对2个综框及其对应的连杆机构分别进行分析。

2.2.1综框16平面连杆机构

提综机构中综框16平面连杆机构包括曲柄摇杆机构、双摇杆机构和综框连杆机构。图3示出曲柄摇杆机构和双摇杆机构运动分析图。

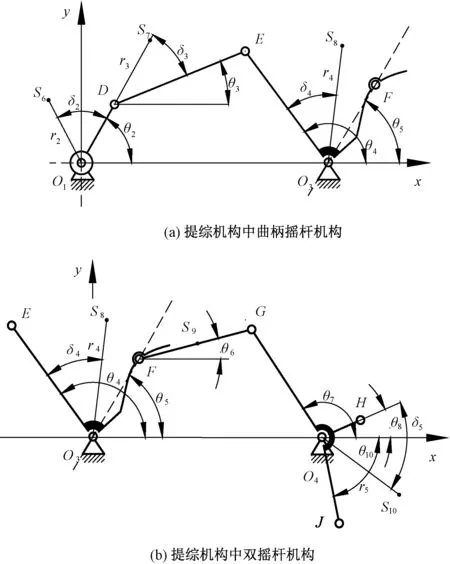
图3 平面四连杆机构运动分析图Fig.3 Kinematic analysis diagram of planar four-bar-mechanism. (a) Crank-rocker mechanism in lifting comprehensive mechanism; (b) Double-rocker mechanism in lifting comprehensive mechanism

偏心盘O1D与旋转轴通过花键连接，旋转轴和滑块架固连，设偏心盘与x轴正方向的夹角为θ2，根据偏心盘与旋转轴的装配关系，可得

(7)

对曲柄摇杆机构和双摇杆机构分别进行运动分析，根据闭环矢量方程O1D+DE=O1O3+O3E和O3F+FG=O3O4+O4G可得

(8)

(9)

其中：

P=2LO1DLO3Esinθ2

Q=2LO1DLO3Ecosθ2-2LO1O3LO3E

N=2LO3FLO4Gsinθ5

V=2LO3FLO4Gcosθ5-2LO3O4LO4G

(10)

(11)

式中：L为对应点之间的距离或对应杆长，根据各连杆尺寸设计结果可得。θ4,θ7∈(-π,π)，θ3,θ6∈[-π/2,π/2]。

(12)

(13)

图4示出综框连杆运动简图。θ9的大小可由θ8求出：

(14)

其中，θ9∈[0,π]。

图4 综框连杆机构运动分析图Fig.4 Kinematic analysis diagram of heald frame linkage mechanism

2.2.2综框25平面连杆机构

综框25对应的偏心盘与x轴的夹角为θ2-π，参考式(7)～(14)，可对综框25平面连杆机构进行运动分析，求出各杆件方位角的变化规律，由于篇幅限制，在此不再一一列出。

至此，可求出旋转式多臂机提综机构各杆件的位置随着大圆盘旋转角度φ的变化规律。

3 提综机构动力学建模

Lagrange方法[12-14]作为一种成熟的系统动力学建模方法，从能量的观点统一建立起来系统动能、势能和功之间的关系，简便快捷。用Lagrange动力学方程对系统进行动力学建模，方程表达式如下：

(15)

式中：L为系统的动势，即动能与势能的差；qi为系统的广义坐标；Fi为系统的广义力；n为系统的广义坐标数。由于系统的自由度为1(即广义坐标数为1)，故可选定大圆盘旋转角φ为系统的广义坐标。

首先对综框16平面连杆机构以及旋转变速机构进行分析，将滚子都假设为凸轮摆臂末端的集中质量。设图1旋转式多臂机提综机构中大圆盘2、凸轮摆臂3及2个滚子4、滑块5、滑块架6、旋转轴7、偏心盘8、环形连杆9、提综臂10、提综连杆11、大刀片12、转臂连杆13、小刀片15、综框16、综框连杆14的质量分别为m1、m2、m3、m4、m5、m6、m7、m8、m9、m10、m11、m12、m13、m14。如图2～4所示，凸轮摆臂、偏心盘曲柄O1D、环形连杆DE、提综臂EO3F、大刀片、小刀片的质心位置及旋转中心连线与构件间的夹角分别为δ1、δ2、δ3、δ4、δ5、δ6，质心到各转动副的距离分别为r1、r2、r3、r4、r5、r6，综框的质心到I点的垂直距离为r7。

将摆臂和滚子视为一体，摆臂及滚子质心S2位置为

(16)

滑块架O1B与x轴的夹角为π/2-α，滑块的质心S3位置为

(17)

偏心盘曲柄O1D与x轴的夹角为θ2，其质心S6位置为

(18)

同理环形连杆DE的质心S7位置为

(19)

提综臂EO3F的质心S8位置为

(20)

连杆FG的质心S9位置为

(21)

大刀片的质心S10位置为

(22)

杆HI的质心S11位置为

(23)

左边小刀片的质心S12位置为

(24)

综框只考虑y方向的位移，质心S13在竖直方向位置为

yS13=LO4Hsinθ8+LHIsinθ9+r7

(25)

杆JK的质心S14位置为

(26)

3.1 提综机构各构件势能

选取xO1z平面为零势能面，多臂机提综机构各构件重力方向沿y轴负方向，由于提综机构中2个凸轮摆臂以及2个滑块关于大圆盘中心完全对称，它们总势能恒定为0。各个构件的重力势能可表示为

Ui=migySi

(27)

其中，i=6,7,8,9,10,11,12,13,14。

3.2 提综机构各构件动能

绕定轴旋转的构件，其动能可表示为

(28)

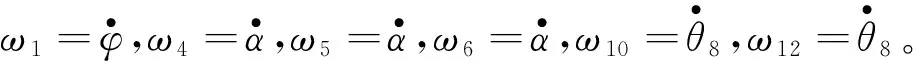
平面运动构件的动能为

(29)

综框只在y方向上运动，其动能为

(30)

3.3 系统动力学模型的建立

旋转式多臂机提综机构中旋转变速机构的总势能恒定为0，所以由式(1)～(30)可得到其动势L1为

L1=T1+2T2+2T3+T4+T5

(31)

综框16平面连杆机构有2个综框连杆和2个小刀片，3个转臂连杆，其动势L2为

(32)

根据2.2.2节对综框25平面连杆机构的运动学分析，参考以上对综框16平面连杆机构的动能势能求解过程，可求出综框25平面连杆机构的动势L3。

提综机构整体的动势为

L=L1+L2+L3

(33)

忽略旋转式多臂机提综机构中各运动副间的摩擦、间隙、杆件变形，假设运动副之间没有能量损耗，系统在空载工况下运行。将式(33)代入式(15)中，可得到旋转式多臂机提综机构大圆盘的驱动力矩：

(34)

4 提综机构动力学仿真与优化

某型号旋转式多臂机提综机构的几何和物理参数如表1所示。由于综框25平面连杆机构的参数和综框16平面连杆机构完全相同，表中不予列出。

表1 提综机构各构件几何参数与物理参数Tab.1 Geometric parameters and physical parameters of lifting comprehensive mechanism′s each component

在MatLab中将表1数据代入式(5)～(34)进行数值计算，设旋转式多臂机空载时电机转速为800 r/min，工作周期为0.15 s，得到旋转轴7的旋转角度、2个综框的竖直位置以及大圆盘的驱动力矩随大圆盘转角变化曲线如图5～7所示。

图5 旋转轴7的旋转角度变化图Fig.5 Rotation angle diagram of axis 7

图6 综框重心的竖直位置变化图Fig.6 Diagram of heald frame′s vertical displacement

图7 大圆盘驱动力矩图Fig.7 Driving torque diagram of large disk

从图5、6可看出，旋转轴7在1个运动周期中停顿2次，对应时间内综框也静止，2个综框的竖直运动距离都为90 mm，与设计目标和实际工况要求相一致[15]。从图7可看出，1个运动周期内，大圆盘前后0.075 s的驱动力矩变化趋势基本相同，这是因为凸轮轮廓线在前后180°完全相同。以上分析初步验证了所建动力学模型的有效性。

根据表1中各零件的参数，可在Pro/E中对旋转式多臂机提综机构进行建模，将所建几何模型导入ADAMS中，对模型重新添加约束，并定义材料属性，最后得到虚拟样机模型如图8所示。

图8 机构ADAMS示意图Fig.8 Diagram of mechanism in ADAMS

运用ADAMS软件进行动力学虚拟仿真[16-18]，软件仿真环境中积分器选择WSTIFF，积分格式选用I3，设置大圆盘转速为400 r/min，得到1个运动周期内大圆盘受到的驱动力矩M，将其与图7中MatLab理论运算结果对比，结果如图9所示。

图9 大圆盘驱动力矩对比图Fig.9 Comparison diagram of large disk′s driving torque

从图9可看出，MatLab中动力学模型计算结果和ADAMS虚拟仿真结果基本一致，但是稍有偏差，这是因为对各个构件的质量以及转动惯量等参数的测量存在误差，且MatLab和ADAMS计算精度不同，这些因素造成的大圆盘驱动力矩的曲线偏差可以忽略不计。可以证明所建立的动力学模型的正确性，同时也验证了ADAMS动力学虚拟仿真的可靠性。

一个运动周期内大圆盘的驱动力矩在-109～115.03 N·m之间变化，力矩有较大波动。驱动力矩的较大波动会造成机构运行速度波动和机构的振动，对旋转式多臂机提综机构稳定运行不利。

4.1 多臂机转速对大圆盘驱动力矩的影响

考虑到大圆盘旋转1周，大圆盘的驱动力矩有较大波动，研究不同转速下大圆盘驱动力矩的变化。运用MatLab软件设定不同的运行速度，分别求出大圆盘的驱动力矩。图10分别示出大圆盘转速在300、400、500 r/min时，大圆盘的驱动力矩，所对应的织机转速分别为600、800、1 000 r/min。

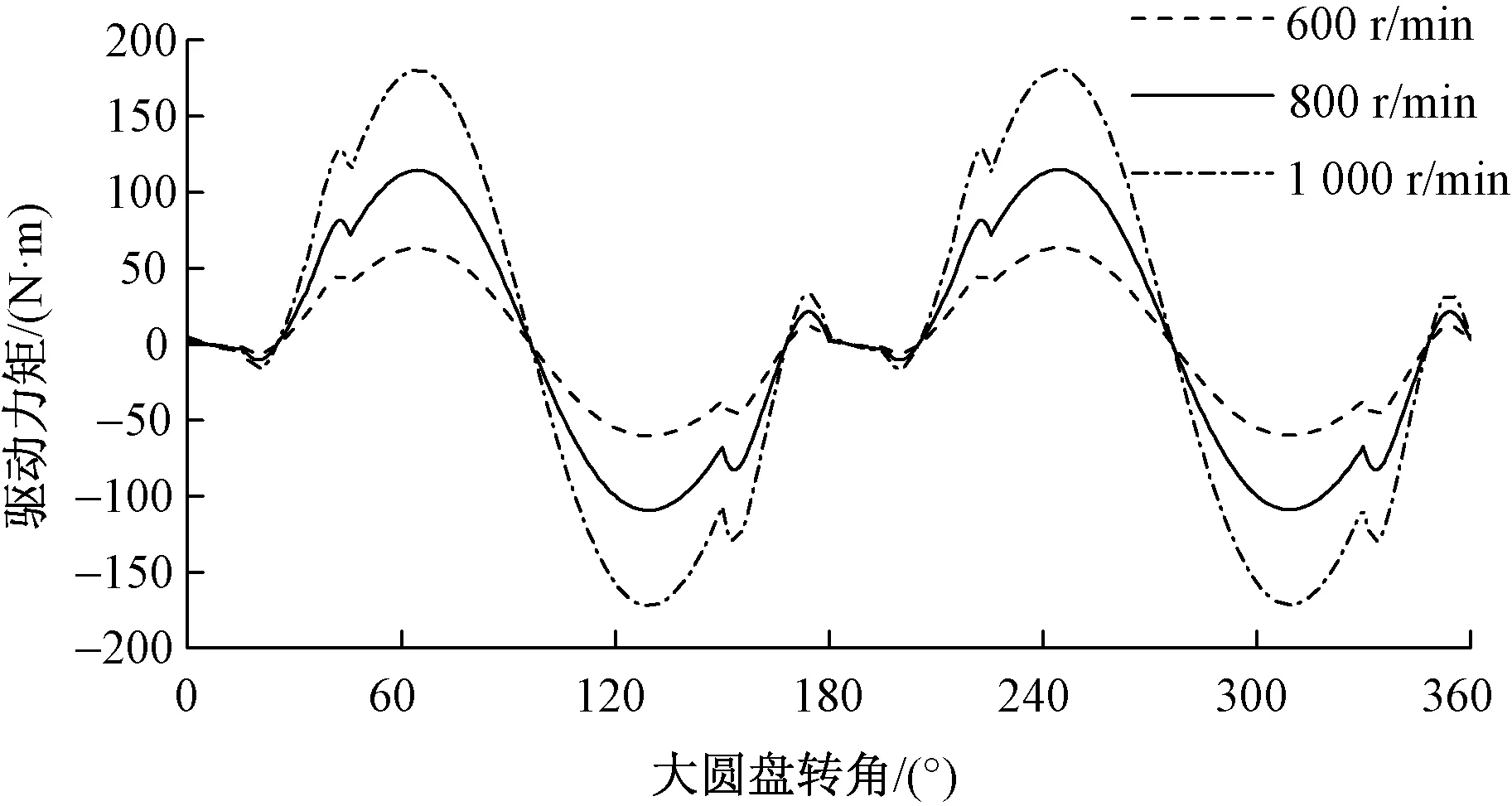
图10 不同转速下大圆盘的驱动力矩Fig.10 Driving torques of large disk at different speeds

对图10进行分析，转速变化时大圆盘的驱动力矩的变化趋势没有改变，但是波动幅值有所不同，转速越大，对应的大圆盘的驱动力矩波动幅值越大，织机转速为1 000 r/min时大圆盘的驱动力矩波动幅值约是800 r/min时的1.58倍，织机转速为800 r/min时大圆盘的驱动力矩波动幅值约是600 r/min时的1.81倍。实际中驱动电动机的驱动力矩波动幅值有限，强行增加运转速度会给电机带来不可逆的损害，所以不能盲目增大旋转式多臂机的转速。要提高多臂机的转速以提高工作效率，提高织机的经济效益，需要对提综机构多方面进行优化。

4.2 综框质量对大圆盘驱动力矩的影响

现有的综框一般都选用铝合金材料，密度约为2 700 kg/m3，普通织机安装4～12片综框，总体提综载荷较大。为研究综框质量对驱动力矩的影响，现选用铝锂合金和镁合金材料综框分别进行仿真，其材料密度分别为2 500、1 800 kg/m3，统一设置织机转速为800 r/min，得到大圆盘驱动力矩，结果如图11所示。

图11 改变综框质量时大圆盘的驱动力矩Fig.11 Driving torques for changing mass of heald frame

由图11可看出：使用铝锂合金材料综框时大圆盘驱动力矩波动幅值比使用铝合金材料时降低6.93%，使用镁合金材料时大圆盘驱动力矩波动幅值比使用铝合金材料时降低27.55%，减小综框的质量可以明显减小大圆盘驱动力矩的波动幅值。所以，选用质量轻的材料来制作综框，可有效改善提综机构的动力学性能。

4.3 综框动程对大圆盘驱动力矩的影响

综框动程直接影响综框的加速度，进而影响综框运动的惯性力。通过调节提综臂与提综连杆连接的转动副位置以调节综框的动程，进而研究大圆盘驱动力矩的变化。统一设置织机转速为800 r/min，减小综框动程为75、60 mm，与动程为90 mm时大圆盘的驱动力矩对比，结果如图12所示。

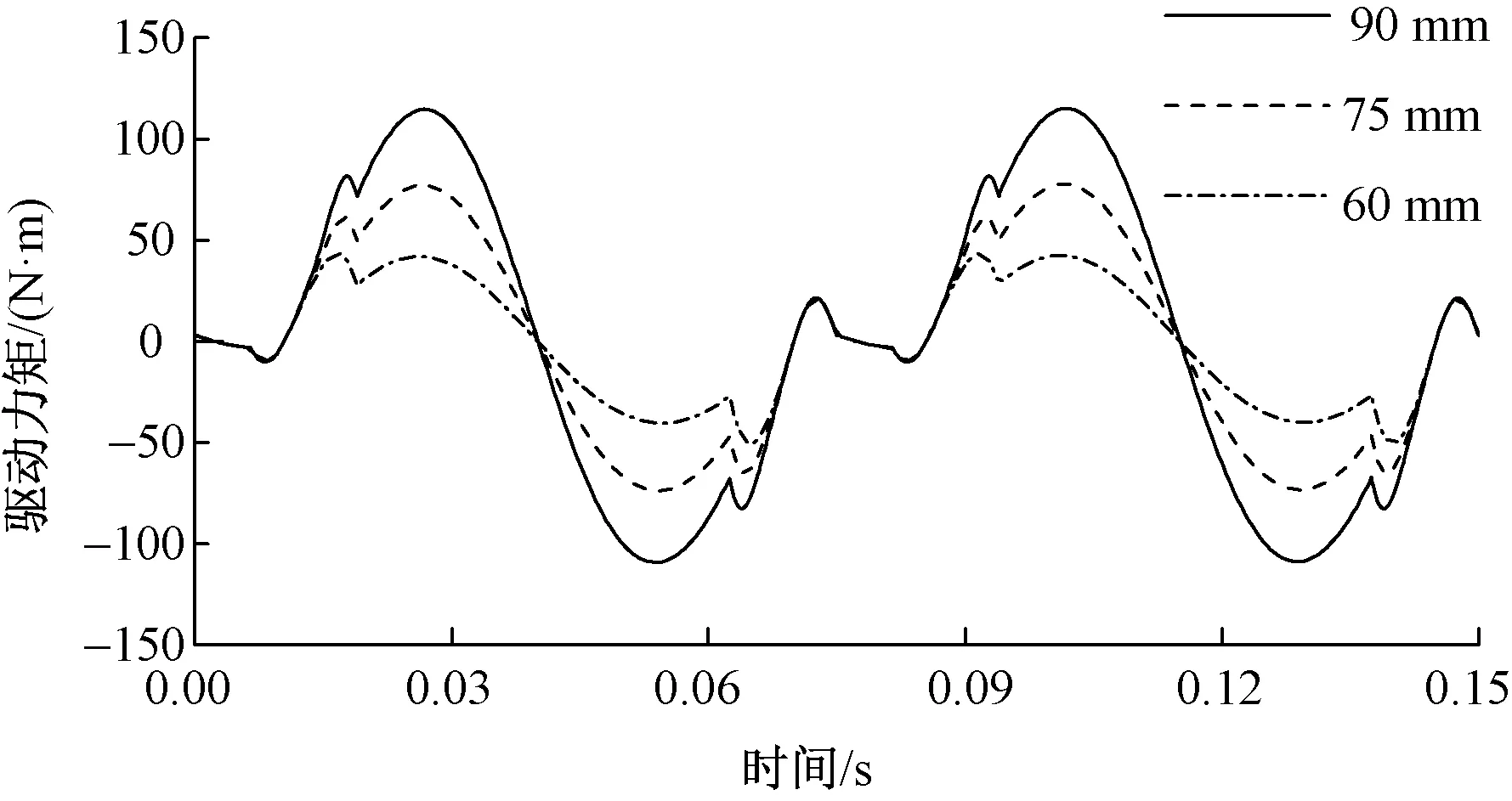
图12 改变综框动程大圆盘的驱动力矩Fig.12 Driving torques for changing heald frame′s movement distance

由图12可看出：综框动程为75 mm时大圆盘的驱动力矩波动幅值比动程为90 mm时减小了32.70%，综框动程为60 mm时大圆盘驱动力矩波动幅值比动程为90 mm时减小了58.89%。综框动程越小，大圆盘驱动力矩波动幅值越小。可见，在符合织机整体工艺要求的情况下，适当缩小综框的动程可以减小大圆盘驱动力矩的波动幅值，优化旋转式多臂机提综机构动力学性能。

4.4 优化凸轮廓线对大圆盘驱动力矩的影响

作为旋转式多臂机提综机构中的核心机构，共轭凸轮廓线形状决定整个提综机构的运动规律，也影响开口动力学性能。由4.1、4.3节分析可知，在各种运行条件下，大圆盘驱动力矩波动幅值比较大，通过改变凸轮轮廓曲线形状来优化提综机构动力学性能。要求旋转轴7的速度、加速度连续，凸轮廓线选用多项式运动规律时，加速度一直不为0，惯性力存在会导致大圆盘驱动力矩增大，所以选用组合运动规律。旋转轴7匀速旋转时，加速度为0，有利于减小驱动力矩，选用五次项修正等速运动规律的凸轮廓线，设计旋转轴7的旋转角度α随大圆盘的旋转角度φ的变化规律如下。

1) 静止区段：

α=0°

(35)

此时φ∈[0°,15.5°)。

2) 加速运动区段：

(36)

式中φ∈[15.5°,45.5°)。

3) 等速运动区段：

(37)

式中φ∈[45.5°,150°)。

4) 减速运动区段：

(38)

式中φ∈[150°,180°]。

改变所建动力学模型中凸轮参数，在MatLab中仿真，设置织机转速为800 r/min，得到大圆盘的驱动力矩与含摆线修正等速运动规律轮廓曲线凸轮的提综机构大圆盘驱动力矩进行对比，结果如图13所示。

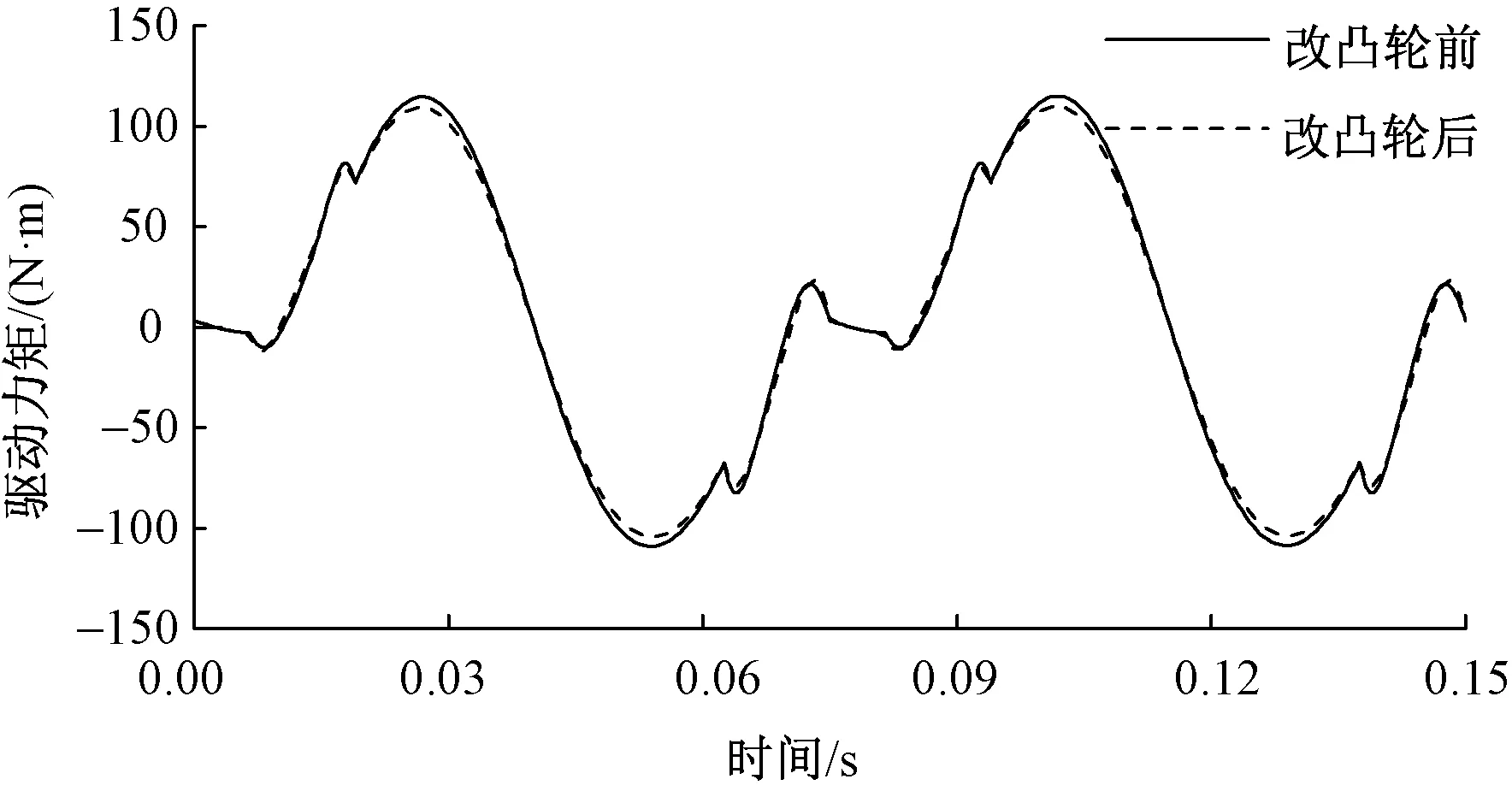
图13 改变凸轮廓线大圆盘的驱动力矩Fig.13 Driving torques for changing the cam profile

凸轮廓线为摆线修正等速运动规律曲线时，驱动力矩上下波动幅值为224.03 N·m，改进后，驱动力矩波动幅值为213.70 N·m，减小了4.61%，由于旋转式多臂机含有多个提综臂，正常工作时可以带动多个综框，所以在正常工况下，提综机构凸轮采用五次项修正等速运动规律廓线可以改善多臂机的动力学性能。

5 多片综框同时运动的处理方法

提综机构所驱动综框的数目随着织机织布纹理的要求而变化，为了提升所建动力学模型的通用性，分析提综机构同时带动2个以上综框的情形，现就所建动力学模型进行推广。

由于每组中综框连杆机构的运动规律相似，可以参考第2节对含2个综框的提综机构运动学分析方法对含多片综框的提综机构进行运动学分析，建立整体动力学模型时，旋转变速机构动势为L1，2组综框中，单个综框平面连杆机构的动势分别为L2和L3，则系统整体的动势为

L=L1+nL2+nL3

(39)

n为每组综框中所含综框的数目，上文中介绍的为n=1时的情况，即提综机构带动2片综框相向运动。

求出整体动势后代入式(15)得到系统整体动力学模型，可对系统进一步优化。

6 结 论

1)设计旋转式多臂机提综机构凸轮的理论廓线，列出了廓线方程，进而建立了机构整体的运动学模型，为动力学模型的构建奠定了基础。

2)运用Lagrange方程建立了旋转式多臂机提综机构的整体动力学模型。应用Pro/E和ADAMS仿真软件建立了该机构的虚拟样机模型，并进行动力学仿真，验证了所建动力学理论模型的正确性。

3) 通过分析不同转速对大圆盘驱动力矩的影响，得出转速越大，大圆盘驱动力矩的波动幅值越大的结论；驱动力矩的大范围波动是制约旋转式多臂机转速提升的重要因素，通过减小综框质量、减小综框运动动程或提综机构凸轮采用五次项修正等速运动规律的凸轮廓线等方法，均可减小大圆盘驱动力矩的波动幅值，有效提升旋转式多臂机提综机构的整体动力学性能。针对本文动力学建模方法，将提综机构带动2个综框向同时带动多个综框运动推广，进一步提升了所建动力学模型的适用性。