应用于海洋工程中水平受荷桩特性分析的修正P-y曲线模型

2018-09-22武亚军＊，卢晨阳，李卫超，杨敏

大连理工大学学报 2018年5期

武亚军＊，卢晨阳，李卫超，杨敏

（1.上海大学土木工程系，上海 200444；2.同济大学地下建筑与工程系，上海 200092；3.同济大学岩土及地下工程教育部重点实验室，上海 200092）

0 引言

随着海洋工程建设的飞速发展，海上建筑物越来越多，由于海洋工程的特殊性，这些建筑物的基础通常都采用桩基础.处于海洋环境中的桩基承受着风、海浪、地震等多种循环水平荷载，这些循环水平荷载的长期作用会导致海洋桩基产生较大的水平位移，当水平位移超过一定范围时甚至会危及海洋工程的安全［1］，为此，对循环水平荷载作用下单桩的位移反应性状进行研究具有很重要的工程实际意义.

为了建立水平位移与循环水平荷载之间的关系，许多学者进行了大量的研究工作，总体上对循环荷载作用下单桩反应性状的分析方法有两种：一种是直接估算桩身位移法［2－3］，另一种是折减P-y曲线法.由于直接估算桩身位移法只是反映了桩身位移随着循环荷载的变化规律，并不能从本质上反映土体间相互作用的变化规律，存在一定的局限性［4］.折减P-y曲线法最早是由Reese等［5］于1974年提出的，它是在一系列试验研究的基础上，直接用不同深度下的桩周土抗力P乘以相对应的经验系数进行折减，并不考虑荷载循环次数、桩基类型等其他因素.随后Fan等［6］通过试验证明Reese方法计算得到的单桩反应性状与实测结果不符，并提出了能同时考虑荷载循环次数和桩基类型等因素的折减方法.之后，为了考虑更合理的影响因素，人们对该方法进行了许多修正，其中，朱斌等［7］于2013年在离心机试验的基础上，基于循环应力比提出了折减系数的新定义，采用这一折减系数的方法所得到的计算结果与实测数据比较吻合，但是该方法对静荷载试验结果依赖性比较大，所需参数也较多，不方便使用.Rosquot等［8］于2013年通过离心机试验提出了一套较为完善的折减方法，该方法是通过一个折减系数r对静力P-y曲线中的P 进行折减，不仅考虑了荷载循环次数的影响，还考虑了荷载幅值因素，通过与试验数据进行对比证明结果更为合理，但是，本课题组采用Rosquot等所提出的折减方法对其他学者的试验结果进行分析时，发现计算结果普遍偏小，而静力P-y曲线模型的选取和折减系数的取值是导致这一结果的两个主要原因.鉴于此，本文基于API规范P-y曲线法对其中的静止土压力系数K0、投影角α和初始地基刚度K进行重新定义和取值，提出修正的P-y曲线模型；并对Rosquot所提出的折减方法中的影响系数a进行改进，并采用修正后的静力P-y曲线模型和改进后的折减系数对两个试验案例［8－10］进行分析，验证该修正方法的合理性.

1 试验案例

本文所选取的两个砂土中的试验案例如下.

第1个试验案例是由李卫超等［9－10］在爱尔兰都柏林市西南方向约25km的一个商业采砂场内做的一个桩基试验，试验编号为T1.该场地地基土由均质密实硅质砂组成，地下水位在地表下约15m处.土体基本参数如表1所示；模型桩为钢管桩，其基本参数如表2所示.Li等在静载试验的基础上，也进行了两组循环荷载试验，本文选取一组进行分析，循环荷载加载过程如表3所示.

第2个试验案例是由朱斌等［7］做的一个离心机模型试验（记为T2），并且给出了对应原型桩的试验参数和试验结果.土体基本参数如表1所示；模型桩为铝管桩（原型桩为钢管桩），基本参数如表2所示.本文选取一组静载试验以及相对应的循环荷载加载试验进行分析，循环荷载比为0.346，荷载循环次数为995次.

表1 土体基本参数Tab.1 The basic parameters of soil

表2 模型桩基本参数Tab.2 The basic parameters of model piles

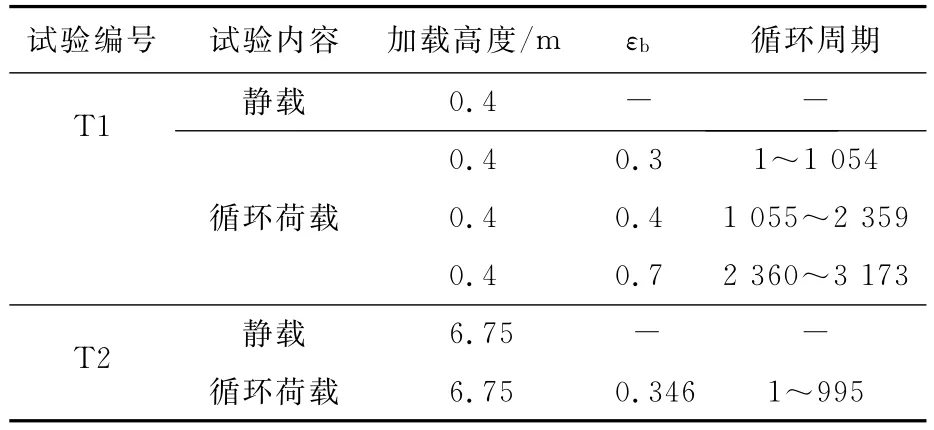
表3 加载过程Tab.3 The loading process

2 修正P-y曲线模型及静力分析

在砂土静力P-y曲线模型中应用最多的是API规范［11］中P-y曲线模型和双曲线P-y曲线模型［7，12］.

2.1 API规范P-y曲线模型

美国API规范最早使用P-y曲线法，已被广泛应用于桩基工程设计中.API规范关于砂土中桩基所受到的水平抗力计算公式如下：

式中：A＝（3－0.8 H／D）≥0.9；K 是指初始地基刚度（kN／m），K＝nz，n是初始地基反力模量（kPa）；z是深度（m）；y是指水平位移（m）；Pu是极限水平承载力（kN），由下式确定：

其中γ是土体有效重度；z是深度；D是桩的直径；C1、C2、C3为有效系数，计算公式如下：

式中：φ为土体内摩擦角；α＝φ／2；β＝π／4＋φ／2；K0为静止土压力系数，取0.4；Ka为主动土压力系数，Ka＝tan2（π／4－φ／2）.

2.2 本文修正P-y曲线模型

许多桩基试验证明API规范中的P-y曲线模型存在诸多不足，特别是对于其中一些参数的确定方法，许多学者进行了一些修正.然而，经过若干对比，作者发现其中静止土压力系数K0、投影角α和初始地基刚度K 是使计算结果偏小的3个主要因素，因此，本文基于目前的研究成果给出3个参数确定方法，并与试验结果进行对比.

对于静止土压力系数K0和投影角α，Li等［10］通过现场试验指出，当前API规范关于α和K0的定义太过绝对化，并不能适用于所有土体.为此，本文做出如下修正：

（1）将土力学中正常固结土的静止土压力系数K0≈1－sinφ′引入到P-y曲线模型中［13］，其中φ′是有效内摩擦角，在砂土中φ′＝φ.

（2）Reese等［5］在1974年给出了α的取值方法，即对于松散砂土，α＝φ／3～φ／2；对于密实砂土，α＝φ／3～φ.本文根据T1、T2试验结果认为α分别取值为αT1＝φ，αT2＝φ／2更为合适.

API规范认为初始地基刚度K和土体深度z呈线性关系［14－17］.然而大量试验结果表明，K 和z呈非线性关系［18］.本文选用 Kallehave等［19］提出的初始地基刚度K的计算方法来修正API规范中的P-y曲线模型，计算公式如下：

其中z0＝D0＝1m.

综上所述，本文对API规范推荐的P-y曲线模型的修正内容汇总见表4.

表4 P-y曲线模型对比Tab.4 Comparison of P-ycurve models

另外，对于式（3）中n的选取也是众多学者一直以来研究的课题.初始地基反力模量n的选取直接影响了土体弹簧刚度的计算值，合适的地基反力模量既能减少计算工作量，也能给出合理的计算结果.

对于T1试验，选取了API规范、Reese和Terzaghi推荐值对n进行对比计算分析.当土体密实度为100%时，API规范、Reese和Terzaghi推荐值分别为75 000、61 000和23 400kPa.由图1发现，T1试验选用API规范给出的推荐值更加合理，即nT1＝75 000kPa.对于 T2试验，Yan等发现API规范中所给出的参考值明显偏大［20］，并由此进行反算得到nT2＝6 770kPa更为合理.

图1 不同n值对计算结果的影响Fig.1 Influence of different nvalues on calculation result

2.3 案例分析与对比

本文采用Matlab编制了修正后的P-y曲线模型的有限元法计算程序，分析了前述两个案例，并与实测数据、API规范方法和双曲线模型的计算结果进行了对比，如图2所示.

图2 静载试验与计算结果对比Fig.2 Comparison of static load test and calculated results

由图2（a）T1试验中实测值与计算值进行对比可以发现，本文修正模型的计算结果在整个加载阶段均与实测值比较吻合，而API规范模型和双曲线模型都是在超过80kN荷载后桩身位移急剧增加，特别是双曲线模型在荷载大于90kN后，桩身甚至发生了破坏.图2（b）T2试验显示，采用本文修正模型时，在4 000kN以下的小荷载作用时，计算结果和实测值符合良好，双曲线模型在4 000kN以上的大荷载作用时和实测值符合良好，而API规范模型的计算结果明显偏于危险.

为定量描述各个P-y曲线模型在各级荷载下和实测值的吻合程度，这里定义了误差率计算公式，即ξe＝（y－y′）／y，其中y为实测位移，y′为计算位移，在此基础上，对各模型计算结果误差进行了分析，误差率曲线如图3所示，从图中可以更为清晰地看出，采用本文所提出的修正模型的计算结果与实测结果最为接近.

图3 计算结果误差率对比Fig.3 Comparison of error rates of calculation results

3 折减P-y曲线模型及循环荷载分析

在静力分析的基础上，用折减P-y曲线法分析单桩水平循环加载试验，选用Rosquot所提出的折减方法，并对其进行改进.

3.1 折减系数

折减P-y曲线法是根据循环荷载作用下静力P-y曲线的变化规律来计算折减后的P-y曲线，以此来估算和预测循环荷载作用下的桩身位移的一种方法.一般是通过折减静力P-y曲线中桩周土的反力P来实现P-y曲线的折减，其实质是对土体弹簧刚度的折减，即在循环荷载的持续作用下，土体弹簧刚度逐渐减小，桩周土反力不断减小，导致水平位移增大.折减P-y曲线法的具体形式如下：

式中：PN是荷载循环N 次后的桩周土反力，P0是静力作用下的桩周土反力，rc是折减系数.

在关于折减系数确定的众多方法中，Rosquot所提出的折减系数可以考虑荷载循环次数（N）和荷载幅值（Fc／Fmax）对土弹簧刚度折减的影响，其表达式如下：

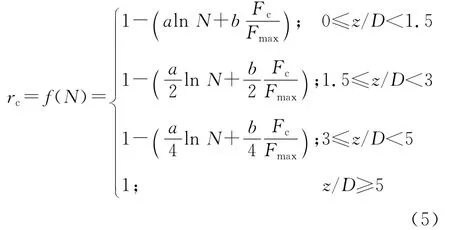
式中：a、b是影响系数，Rosquot给出的参考值为a＝0.034，b＝0.24；Fc＝（Fmax＋Fmin）／2，Fmax、Fmin分别为循环过程中荷载的最大值和最小值.

3.2 考虑多级循环荷载时的折减系数

在实际工程中单级循环荷载作用的情况并不多见，桩基通常承受多级循环荷载的作用，因此，有必要给出多级循环荷载下折减系数的确定方法.本文基于Li等［10］的数值分析结果，在折减P-y曲线法的基础上提出了考虑多级循环加载时折减系数确定方法，为保证后一阶段荷载施加下位移的连续性，分以下两种情况考虑：

（1）如果第一阶段荷载F1在第N次循环结束后的位移最大值yF1，N没有超过第二阶段荷载F2静力作用下的位移yF2，即yF1，N≤yF2，则荷载F1在N次循环后再施加荷载F2，计算第二阶段循环荷载F2作用下的桩身变形时，可以忽略荷载F1在N次循环后对土体刚度的折减，即不考虑多级加载对折减系数的影响.折减系数的公式如下：

式中：N为荷载循环次数，N1为第一阶段荷载循环次数的最大值.

（2）如果第一阶段荷载F1在第N次循环结束后的位移最大值yF1，N超过了第二阶段荷载F2静力作用下的位移yF2，即yF1，N＞yF2，则荷载F1在N次循环后再施加荷载F2，计算第二阶段循环荷载F2作用下的桩身变形时，要考虑荷载F1在N次循环后对土体刚度的折减，即考虑多级加载对折减系数的影响.折减系数的修正公式如下：

式中：N′是指第一级荷载循环N1次结束后，等同于第二级荷载循环N′次对土体刚度的影响，即第二级荷载独立循环N′次后，桩身位移开始超过第一级荷载循环N1次后的位移.

3.3 基于Rosquot折减系数的案例分析

将Rosquot提出的折减方法分别应用于前文中提到的API规范、本文修正和双曲线3种静力P-y曲线模型中，得到了试验T1、T2中的桩在循环荷载作用下不同循环次数时的桩头位移，并与实测值作了对比，如图4所示.

从图4（a）T1试验案例可以看出，API规范和双曲线模型在小荷载循环时，计算结果小于实测值，而在大荷载循环时，桩头位移发生激增，甚至超过实测值，这个变化趋势与前文两个静力P-y曲线模型的变化规律一致.而本文修正模型所得到桩头位移变化不是十分剧烈，相对平稳，计算结果均处于实测曲线的下方.从图中还可以看出，本文修正模型得到的计算结果开始与实测初始值比较接近，随着循环次数的增加，位移也在增加，但是增加速率比较慢，很快趋于稳定，从而使计算结果在数值上整体小于实测结果.

从图4（b）T2试验案例可以看出，3个静力模型分析单级循环荷载所得到的计算结果与静力计算结果（图3（b））的规律一致，所以，可以认为Rosquot折减方法的准确性在一定程度上依赖于所选取的静力P-y曲线模型.

从图4（a）和图4（b）均可以看出，采用Rosquot的折减方法得到加载点位移及其增加速率普遍偏小，而且位移很快趋于稳定，因此，采用Rosquot的折减方法是偏于危险的.这主要是由于所给出的折减系数偏小，不能更好地反映土体弹簧刚度的折减情况，为此，本文对Rosquot的折减方法进行了改进，并通过实测数值进行验证.

图4 循环加载试验计算结果对比Fig.4 Comparison of calculation results of cyclic loading test

3.4 改进Rosquot折减系数及其验证

在Rosquot给出的折减系数的定义式（5）中，a、b两个系数对折减系数影响很大，为了考查这两个系数分别对折减系数及其变化规律的贡献，本文对于a、b取不同值时，在循环次数逐渐增加的情况下折减系数的变化规律进行了研究，如图5所示，从中可以发现：（1）随着a的增大，折减系数随之减小，并且随荷载循环次数的减少减小速率有所增大；（2）b仅仅影响折减系数的数值大小，随着b的增大，折减系数减小，但减小的速率没有变化.因此，鉴于a对折减系数的影响大，b对折减系数的影响小，这里仅对系数a进行改进.

图5 a、b对折减系数的影响规律Fig.5 The influence law of aand b on reduction coefficient

为了更直观反映a对折减系数的影响规律，把每条位移曲线拟合为幂函数，然后进行求导，对比曲线斜率即位移增长率δy的变化.如图6所示，从中可以看出，实测增长率介于a＝0.090和a＝0.100的计算位移增长率之间.

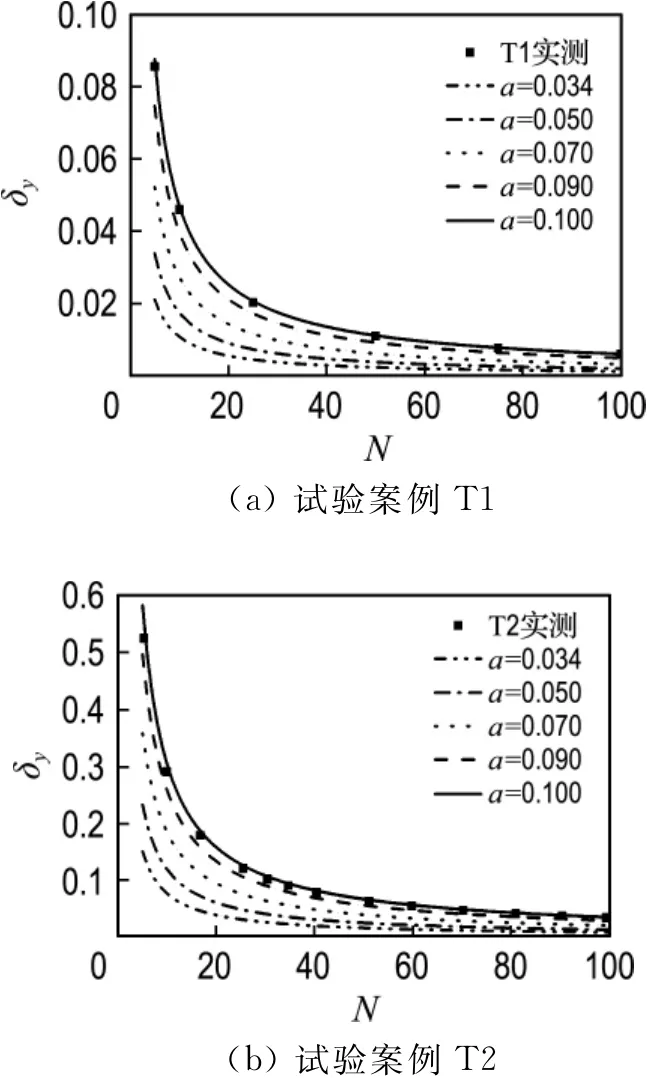
图6 系数a对位移增长率的影响Fig.6 The influence of coefficient aon displacement growth rate

为了得到确切的a值，这里采用了最小二分法，反拟合计算得到a＝0.095，这时位移增长率最符合实测结果.因此，本文认为a取0.095、b取0.24比较合适.

得到新的影响系数之后，采用改进后的折减系数计算公式，并基于本文前面所提出的静力修正API模型对T1、T2两个案例中在循环荷载作用下受荷桩的桩身位移进行了分析，结果如图7所示.

从图7（a）可以看出，T1试验案例中改进后的折减系数计算结果显示，除了大荷载区间位移随荷载循环次数增长与实测值有些偏离之外，在其他小荷载区间均与实测值吻合良好；从图7（b）可以看出，T2试验案例中位移值的增长趋势和实测值大致接近，但在数值上和实测结果存在一定的偏差，由前述可知，这一误差主要是由于静力阶段计算结果所带来的，与折减系数的改进关系不大.总体上来看，采用静力修正API模型和基于Rosquot方法的改进折减方法来分析循环荷载作用下桩身位移是比较合适的.