深覆盖软土场地弹塑性反应谱分析

李英成，张艳娟

（1重庆市建筑科学研究院，重庆 400015；2华润置地（重庆）有限公司，重庆 400050）

0 引言

近年来，随着我国经济高速发展，一些重大工程如高层结构、超高层结构等自振周期较长的复杂结构在沿江、沿海地区相继建成。这些重大工程很多都建于第四纪覆盖层厚达数十米甚至数百米的深覆盖软土场地上。对于这些建于深覆盖软土场地上的重大工程，场地设计反应谱的确定事关工程的地震安全，应引起足够的重视。

随着结构抗震理论的发展，人们逐渐意识到考察结构的抗震性能不仅仅应该考虑结构的弹性地震反应，也应该考虑到结构的弹塑性地震反应。研究者们从不同的角度衍生出多种形式的弹塑性设计反应谱[1-5]。弹塑性设计反应谱种类繁多，一般采用的是等延性强度需求谱，即地震力折减系数R与延性系数μ、结构周期T之间的关系，简称R-μ-T关系。近40年来国内外地震工程研究者对弹塑性设计反应谱的研究，主要就是研究R-μ-T关系。

由于在目前的强震记录库中，虽然深覆盖软土场地上获得的强震记录逐渐增多，但依然十分有限。此时，可以通过实测的基岩地震动经过典型的深覆盖软土场地地震反应分析后得到的地表加速度响应来分析。本文将基于典型深覆盖软土场地和汶川8.0级地震实测地震动记录，对得到的地表加速度响应进行弹塑性反应谱分析，探讨深覆盖软土场地的弹塑性反应谱特征参数，为深覆盖软土场地上的结构抗震设计等提供参考。

1 深覆盖软土场地弹塑性反应谱计算

1.1 深覆盖软土场地地震动数据

选取黄雨[6]等根据直至基岩的整个上海覆盖土层勘察资料和现行上海地基基础规范，设计的一个覆盖层厚度280m，适用于上海市市区的典型地质剖面作为分析场地。

在汶川8.0级地震中，在不同震中距处分别获得了珍贵的基岩地震动实测记录，这些记录较为真实地反应了我国地震动的衰减关系。为了考虑设计地震分组的影响，本文选取了震中距分别为40km、220km及540km处的实测基岩地震动[7]，基于文献[7]提出的可以实现地震动强度频率非平稳的地震动合成方法合成了各30条基岩地震动样本，通过典型深覆盖软土场地[6]的地震反应计算得到地表处的加速度响应各30条作为下一步反应谱分析的地震波。限于篇幅，只给了不同震中距处地表加速度响应各一条，见图1、图2所示。

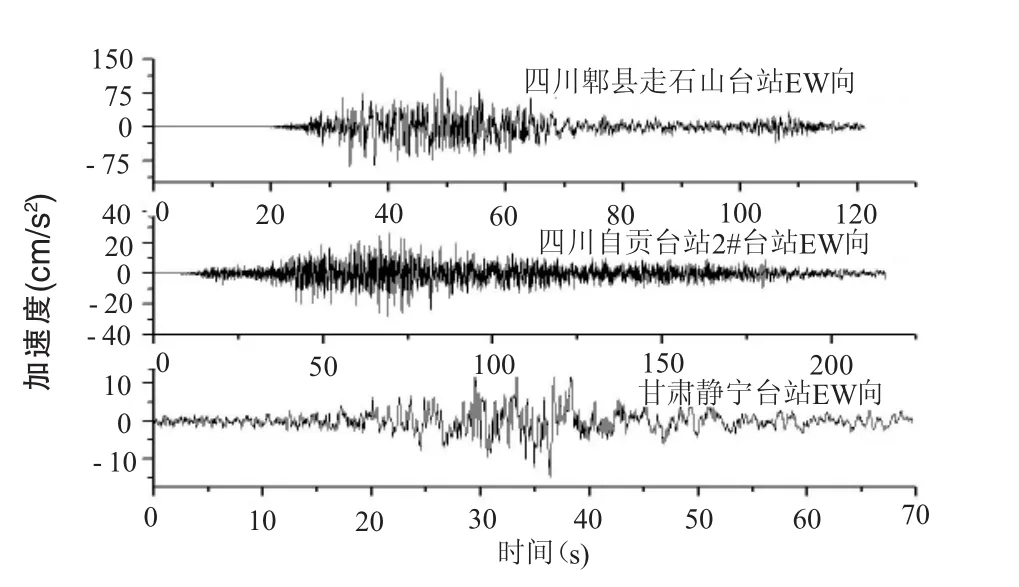
图1 汶川地震实测基岩地震动

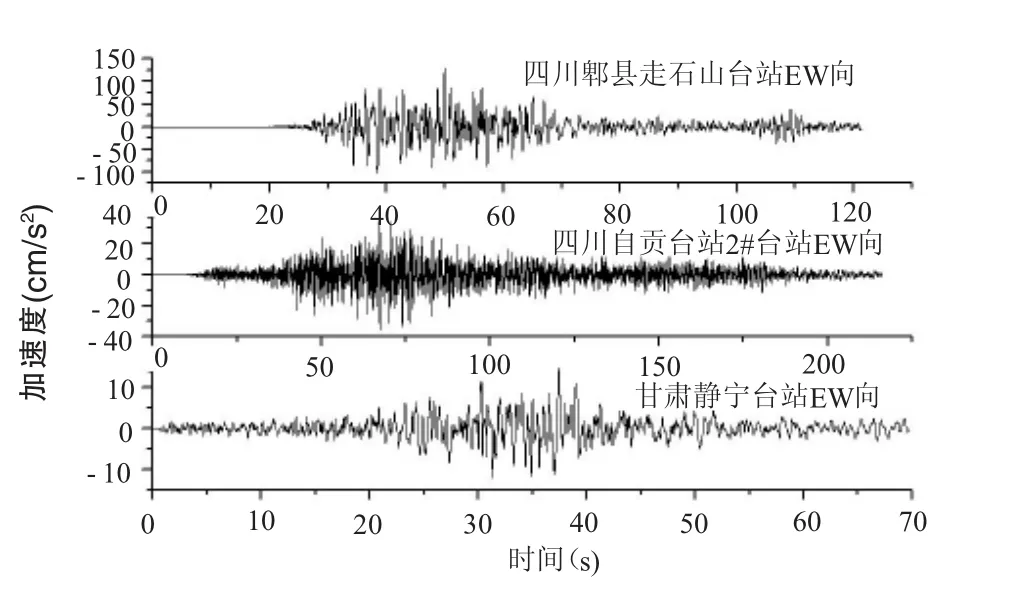
图2 地表自由场加速度响应时程曲线

1.2 地震力折减系数关系分析方法

目前进行结构抗震设计时，如果直接对结构进行非线性时程分析计算，则往往会带来很大的计算量并非常耗时，所以目前国内外的建筑抗震设计规范往往均采用先由弹性设计反应谱理论计算结构的弹性地震力，然后通过地震力折减系数Rμ对其进行折减，以反应结构弹塑性变形和耗能能力对地震力的影响。在地震作用下，单自由度体系的动力平衡方程为：

其中，m为系统质量，x为系统相对位移，c为系统阻尼，F(k，x)为结构恢复力，k为切线刚度，a¨g为地震加速度。

对于具有一定延性的结构，如果非线性系统的屈服荷载非常小，在地震力作用下，系统产生的弹塑性位移变形将非常大，从而超出了结构的延性。为了使结构的变形在容许的范围之内，结构的屈服荷载就必需满足结构延性的要求。对于特点的延性μ，系统所需的最小屈服荷载记为Fy，而系统弹性反应产生的最大荷载记为Fe，则系统在某条地震波下的地震力调整系数Rμ定义为：

Rμ的计算流程如图3所示，在单自由度体系动力特性已知的情况下，计算得到其在地震波作用下的最大荷载Fe和给定延性μ下的屈服荷载Fy，进行得到该延性系数下的R-μ-T关系。

在图3中，当体系的延性μ=1时，结构为无限弹性体系，即Fy(μ=1)=Fe，Fy(μ目标）为给定延性系数下该结构的屈服荷载，即按此屈服强度设计的结构的延性为μ。在本文的分析中，需用的恢复力滞回模型为Clough模型。关于滞回模型对地震力折减系数的影响，在以往的研究中一般认为滞回模型中强度退化和刚度退化对地震力折减系数的影响几乎可以忽略，采用理想弹塑性滞回模型会得到保守的结果。因此，在本文中采用Clough模型，一方面可以较好地模拟钢筋混凝土的滞回特性，另一方面也可以得到较为保守的结果。同时，为了考察不同阻尼比对地震力折减系数的影响，分别选用阻尼比ξ为0.02和0.05来进行分析。

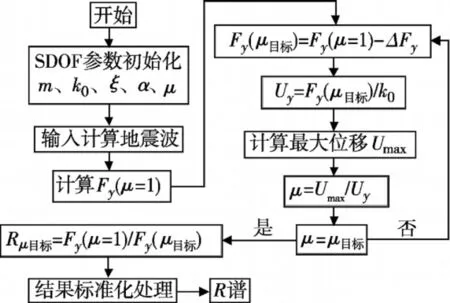
图3 地震力调整系数Rμ计算框图

2 基于不同设计地震分组的深覆盖软土场地弹塑性反应谱特征

在上节中的依据典型深覆盖软土场地地震响应得到的40km处、220km处和540km处的地表加速度反应各30条，对应的设计地震分组分别为第一组、第二组和第三组。在这一节中，分别对具有不同自振周期的单自由度体系在各地表加速度反应作用下进行非线性动力分析，计算其不同延性系数下的地震力折减系数，对每一组30条地表加速度反应计算得到的关系R-μ-T平均后得到具有统计意义的R-μ-T关系，如图4、图5所示：

从图4、图5可以看出，无论是哪一个设计地震分组的R-μ-T关系都满足如下的一般基本特点：

（1）随着延性系数的增大，平均地震力折减系数也变大；

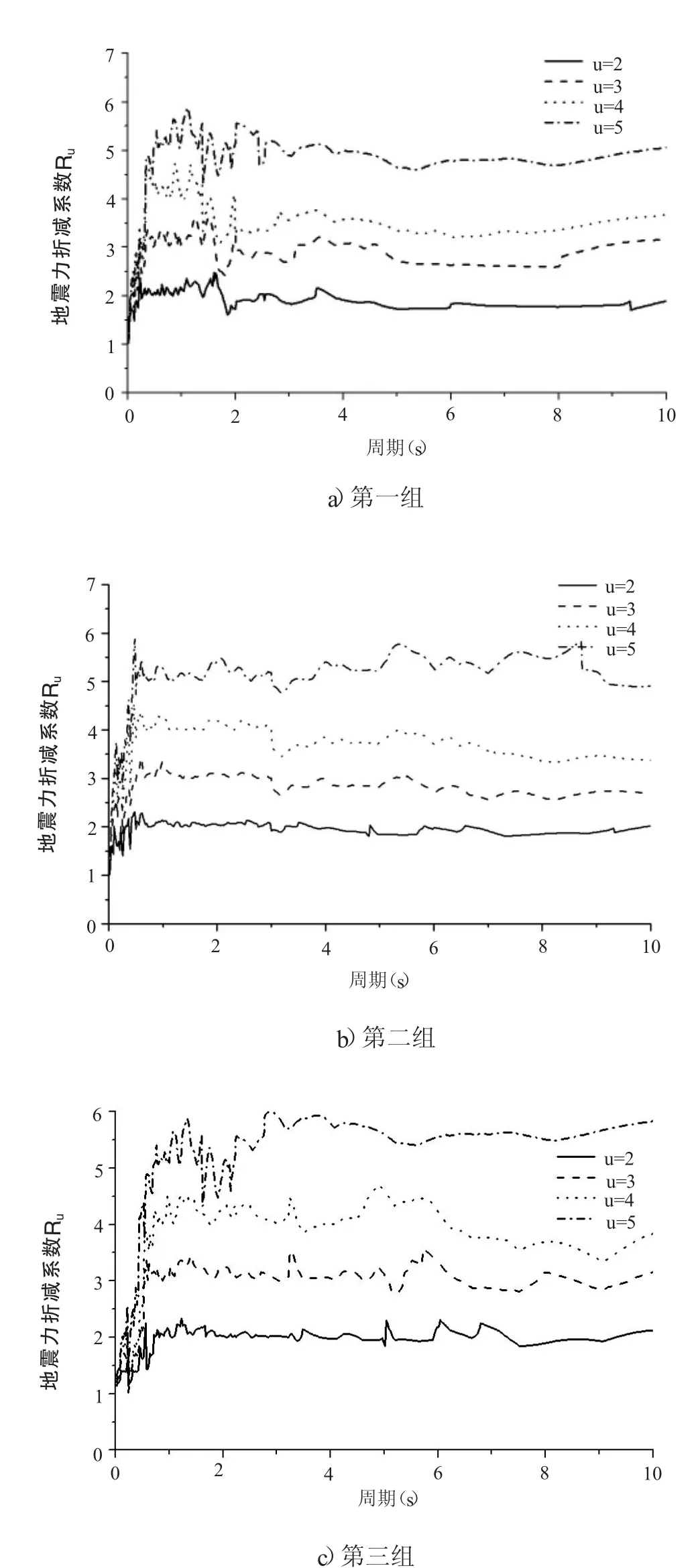
图4 阻尼比为0.05时R-μ-T关系

（2）在短周期内，平均地震力折减系数随周期的变化明显；在长周期段，则基本满足等位移准则，即平均地震力折减系数等于延性系数；

（3）阻尼比对与地震力折减系数的影响明显，在等延性系数的条件下，阻尼比为0.02时的地震力折减系数要大于阻尼比为0.05时的地震力折减系数。

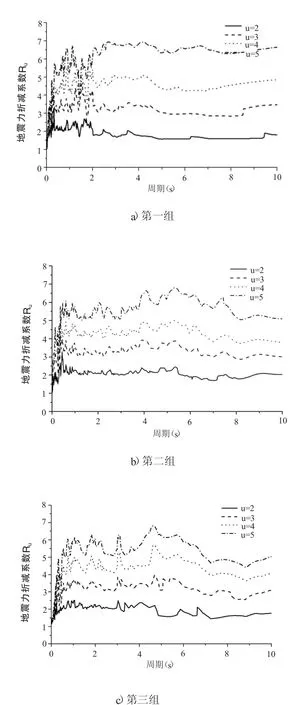
图5 阻尼比为0.02时R-μ-T关系

在以往的研究中，大部分的研究集中在不同场地条件下来考察R-μ-T关系，而忽略了不同设计地震分组对R-μ-T关系的影响。为了考虑设计地震分组对深覆盖软土场地R-μ-T关系的影响，图6分别给出了不同延性系数下，不同设计地震分组下的平均R-μ-T关系，其中阻尼比取为钢筋混凝土结构普遍采用的阻尼比0.05。

从图6可以看出设计地震分组对R-μ-T关系具有一定的影响，主要表现在：

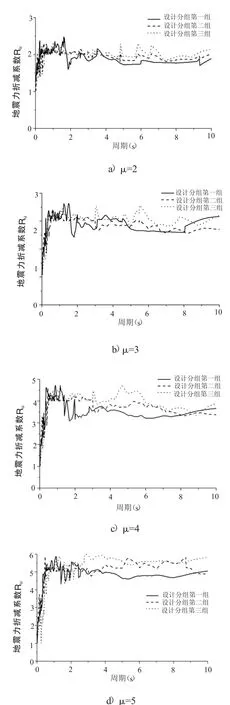
图6 不同延性系数下的R-μ-T关系

（1）在等延性系数下，不同设计地震分组下的R-μ-T关系满足等位移准则的起始周期具有较大区别，一般性地认为可选取不同设计地震分组的特征周期Tg作为起始周期（其中设计地震分组第一组对应为0.78s、第二组为0.94s、第三组为1.48s）。

（2）在等延性系数下，在短周期段内，设计地震分组第一组对应的地震力折减系数最大，而设计地震分组第三组对应的地震力折减系数最小；在长周期段上，则设计地震分组第一组对应的地震力折减系数最小，而设计地震分组第三组对应的地震力折减系数最大。

（3）随着周期的变大，设计地震分组第一组对应的地震力折减系数衰减得最快，设计地震分组第三组对应的地震力折减系数衰减得最慢。

3 基于不同设计地震分组的深覆盖软土场地弹塑性反应谱拟合

为了便于结构抗震分析的使用，有必要对之前获得的平均R-μ-T关系曲线进行拟合。在进行曲线拟合时，需要首先确定其拟合函数。一般认为，地震力折减系数受多种因素影响，其取值不但与震级、震源机制、地震波传播途径、地震动持时、场地条件、阻尼比、滞回模型、屈服后刚度、位移延性等相关，还与系统的初始弹性自振周期相关，而上述的这些参数实际上也并不是相互独立的。在以往的研究中，Miranda[7]发现，在场地条件相同的情况下，对于单自由度延性系统，滞回模型、屈服后刚度等的影响几乎可以忽略；此外，还有众多研究[1-3]也得到了基本类似的结论。

同时，地震力折减系数函数需满足这样几个条件：

（1）当T→∞时，即结构为无限柔性结构时，Rμ=μ，即符合“等位移原则”；

（2）当T→0时，即结构为无限刚性结构时，Rμ=1，即对于周期很短的结构其反应必须保持在弹性范围之内，因为对于周期很短的结构，结构地震力即使折减一点，也会带来很大的弹塑性变形，从而导致无法到达其延性要求。

（3）当T＞0时，Rμ≥1；

（4）当μ=1时，Rμ=1。

上述的前两个条件可看成是地震力折减系数应该满足的两个物理边界条件。后两个条件式则可认为是需要满足的数学条件。

基于此，卓卫东，范立础等[4]基于分离变量法提出了如下的拟合函数：

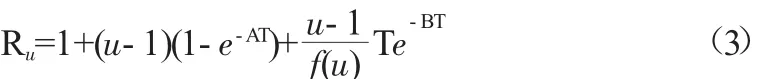
式中，A，B为非线性拟合参数，f(μ)为线性多项式拟合函数。显然，上述拟合函数满足上述的四个基本条件。而在他们的研究中，由于四类场地上获得的实测地震波太少，因此在文献[4]中，只给出了一类、二类、三类场地上的地震力折减系数的函数表达式。

Krawinkler[5]提出了其函数表达式为：

在Krawinkler提出的拟合函数中，并没有考虑地震动特性对地震力折减系数的影响。

在本文的研究中，通过设计地震分组来考虑输入地震动特性的影响（震级、震源机制、地震波传播途径、地震动持时），其中主要通过不同地震设计地震分组对应的特征周期来考虑，分析时也采用统一的阻尼比0.05，因此，对应于深覆盖软土场地，提出的地震力折减系数Rμ的函数表示为：

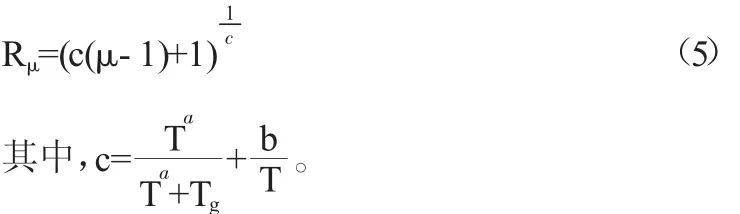
从式（5）可以看出，其满足上述的四个基本条件式，相比较于Krawinkler提出的拟合函数，它考虑了输入地震动特征周期的影响，从而考虑了设计地震分组对地震力折减系数的影响。基于上述三个拟合函数，本文对得到的平均地震力折减系数进行了拟合，其中拟合曲线见图7所示，拟合参数结果如表1所示。

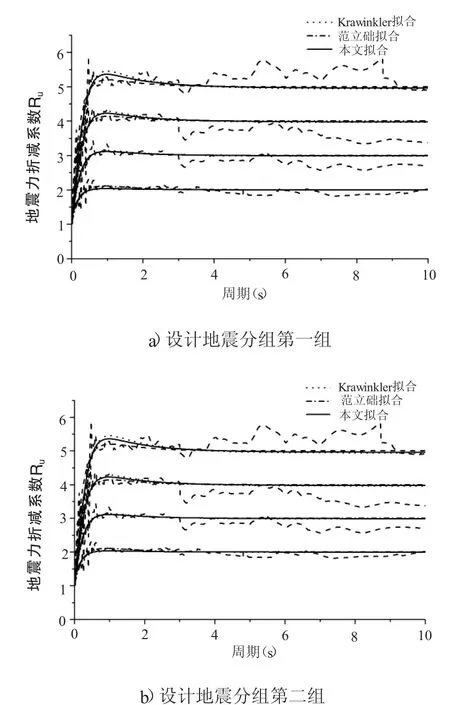
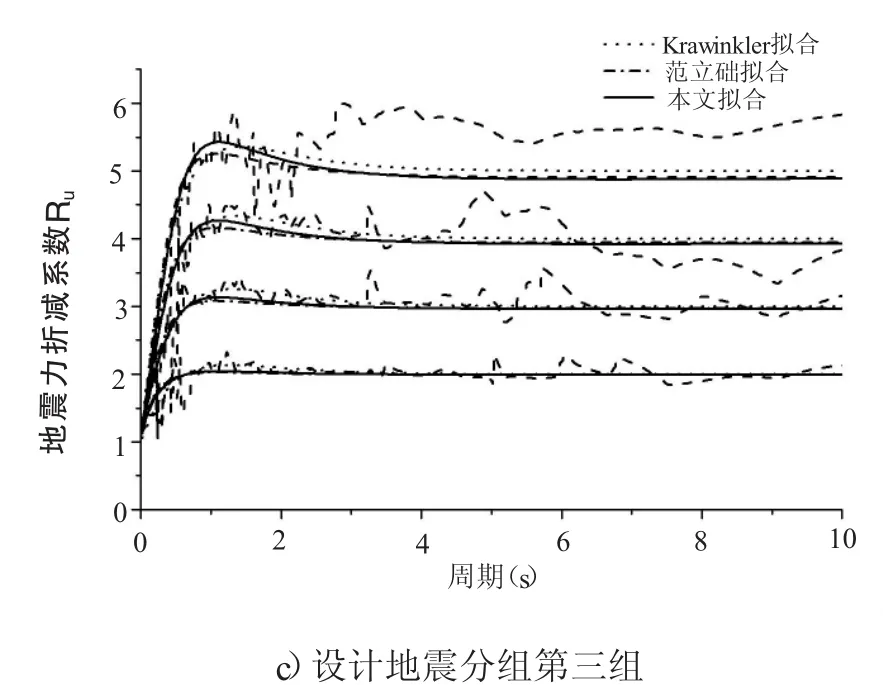
图7 考虑设计地震分组的拟合R-μ-T关系

从上述图表可以看出：总体上，根据本文提出的拟合函数拟合的地震力折减系数曲线与根据krawinkler和范立础提出的拟合函数拟合的地震力折减系数曲线变化一致。当延性系数较低时（μ=2、3），三者之间的差别并不大；而当延性系数较大时（μ=4、5），三者之间存在差别。当结构周期较小时，可不是一般性地认为T＜Tg时，范立础拟合公式拟合出来的地震力折减系数最小，其次为krawinkler拟合公式拟合结果，根据本文拟合公式拟合出来的地震力折减系数最大。当结构为中长周期结构时，krawinkler拟合公式拟合结果最大，其次为范立础拟合公式拟合结果，本文拟合公式拟合结果最小，说明本文拟合公式拟合的结果是最偏于安全的。

4 结论

通过对弹塑性设计反应谱的研究发现：

1）随着延性系数的增大，平均地震力折减系数也变大。在短周期内，平均地震力折减系数随周期的变化明显；在长周期段，则基本满足等位移准则，即平均地震力折减系数等于延性系数。

2）等延性系数下，在短周期段内，设计地震分组第一组对应的地震力折减系数最大，设计地震分组第三组对应的地震力折减系数最小；在长周期段上，则设计地震分组第一组对应的地震力折减系数最小，设计地震分组第三组对应的地震力折减系数最大。随着周期的变大，设计地震分组第一组对应的地震力折减系数衰减得最快，设计地震分组第三组对应的地震力折减系数衰减得最慢。

3）通过与其他研究者提出的拟合函数及结果比较分析可知：本文提出的拟合函数满足相应的物理边界条件和数学边界条件，同时考虑了设计地震分组和场地特征周期的影响，可作为深覆盖软土场地结构地震反应谱分析研究的参考。

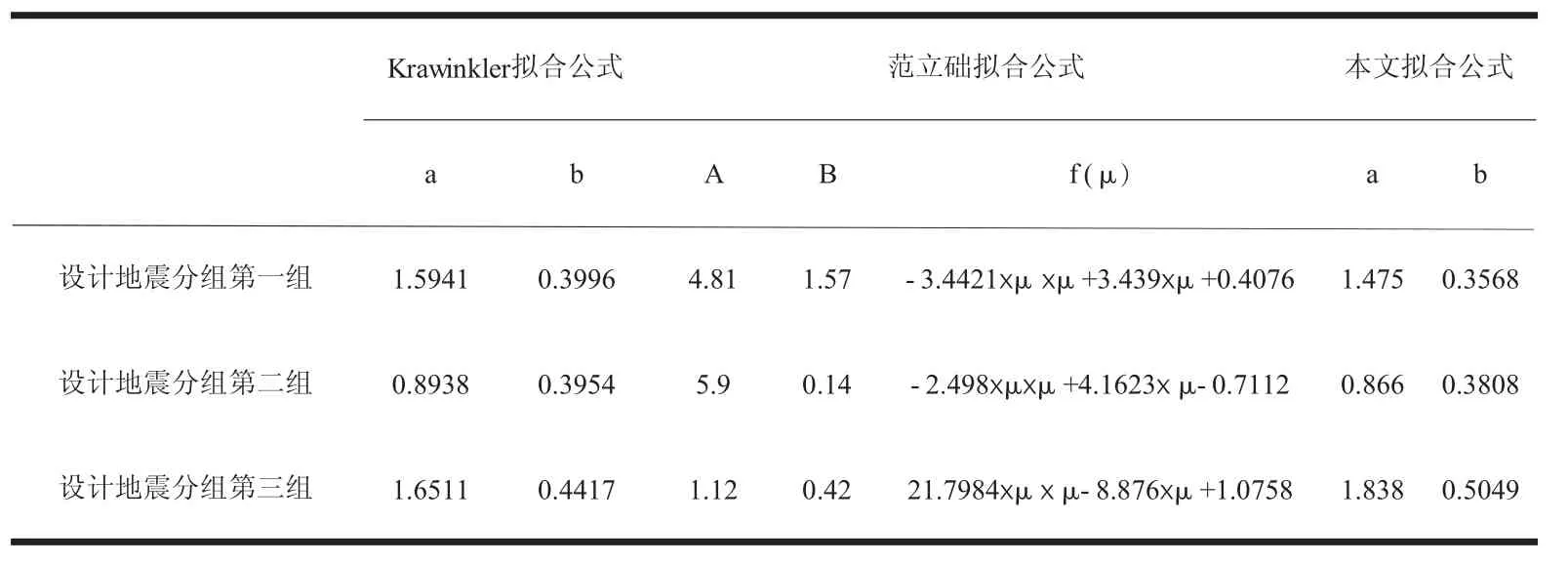
表1 不同设计地震分组拟合得到的地震力折减系数谱参数