一种基于容错和扰动补偿的列车制动控制策略研究

马得银，常 怿

(洛阳铁路信息工程学校，河南 洛阳 471000)

铁路交通的迅速发展给研究人员和铁路工业带来新的挑战，基于安全、快速和精确制动控制的列车自动控制系统成为研究热点[1]。目前列车制动系统通常基于列车制动模型而设计，这种设计方法的好处在于能够最大限度地对列车制动系统的优势进行分析和利用，并结合模型近似求解的算法对列车制动过程进行仿真模拟，优化列车制动系统的性能[2-3]。但是在列车实际运行过程中，基于模型设计的列车制动系统需要面对一些不确定因素，如故障扰动和测量数据失真等，因此需要引入一些机制对这些扰动进行估计和补偿，以提高列车制动系统运行的稳定性[4-5]。

文献[6]针对列车制动系统经常发生的车轮阻塞干扰导致的制动距离和位置测量错误进行量化分析，并利用量化分析结果对测量传感器的数据进行校正。文献[7]基于对牵引控制系统中的传感器进行分析，提出一种基于模糊数学的制动模型。文献[8]在对列车进行故障诊断的基础上，对列车制动系统进行故障补偿，最大限度降低制动过程中意外因素对制动效果的影响。

通过对上述研究成果的分析，基于对列车制动过程中扰动因素的考虑，本文提出一种基于故障容错和扰动补偿的列车制动控制策略。该控制策略利用基于列车运行参数构建的理想化列车参照系统为制动控制系统提供目标控制值，并通过制动模型和容错机制对测量数据的误差以及故障干扰进行补偿，采用基于PI控制器的闭环控制系统实现了具有较强抗故障干扰的列车制动控制模型。最后通过仿真分析对模型的有效性和抗干扰性能进行证明。

1 列车制动系统模型

1.1 列车故障模型

处于正常运动状态中的列车其运动方程为[9]：

(1)

式中：v为速度，m/s；x为车辆的位置,m；w(v)为特定的外部阻力；b(v)为最大制动力；Ub为相对制动力；f(v)为特定的最大牵引力；Um为相对牵引力；g(x)为列车的一般外部阻力。

基于对外部扰动因素的考虑，对列车运动模型进行修正。首先对列车运动阻力之一的动态摩擦力进行近似估算[10]：

w(v)=w0+w1v+w2v2

(2)

式中：w0，w1，w2分别为静态黏着系数、匀速黏着系数和加速度黏着系数。

u为制动或牵引系数，当u<0时表示制动系数，当u>0时表示牵引系数。

另外，列车运行过程中的一般外部阻力将被忽略。因此本文所讨论的列车在进站时为行驶于平坦地面且处于能见度最大化的直线行驶过程中。

由上所述，在没有故障的情况下列车运动的向量方程为[11]：

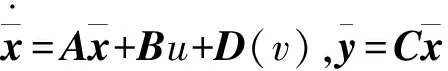
(3)

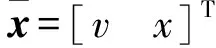
D(v)=[d(v) 0]T，d(v)=-w0-w2v2

(4)

列车在运动过程中的故障主要有制动器故障、系统故障或传感器故障[12]。当列车开始制动时，这些故障就会对列车的制动性能产生影响。基于不同的故障类型，故障模型可以概括为以下3种形式。

第一种是带有故障指示开关的混合制动系统。制动系统还未发生故障，且u<0，则制动系统故障模型如式(3)所示。

当制动系统已经发生故障，且u<0，则制动系统故障模型为：

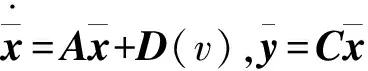
(5)

第二种是列车制动系统出现外部因素导致的故障。这种情况下，需要在列车模型中引入能够表示外部故障特征项。

(6)

式中：F(u)f表示外部故障特征项，其中f表示外部故障发生的概率。如果u<0，则F(u)=-γBu；如果u>0，则F(u)=0。其中γ∈[0,1]，为故障对列车制动系统的影响程度。如果γ=1,则表示故障对列车制动系统具有全局性的影响，并且列车自动控制系统对制动系统失去控制。

第三种是传感器故障。这种故障体现在故障模型的输出中所增加的故障项。

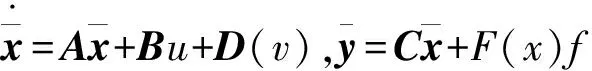
(7)

1.2 制动控制系统架构

在实际应用中,动态摩擦的一部分力d(v)无法运用现有的传感器技术实现精确测量，只能通过式(2)进行近似估算，因此有必要通过其他技术来提高估算的准确度[13]。鉴于此，本文提出一种通过构建输入观察器的方法来实现对动态摩擦力的测量。

另一个问题是当制动系统发生故障导致制动系统失去可控性时，列车自动控制系统不能根据常规控制策略进行动态摩擦补偿[14]。

此外，如果由于车轮传感器受到物理效应的干扰导致测量数据出现偏差，其结果是在列车接近下一个可校准位置数据的信标之前都不能获取准确的列车实际位置轨迹。而列车位置误差随故障持续时间的增加而增大。因此需要尽可能快地检测到所发生的故障,从而触发控制动作，抑制故障，减少位置误差[15-16]。

基于对上述实际问题的考虑，本文构建一个理想化的参照系统，为列车制动系统提供速度参考值以及准确的停车位置等控制器的目标值。随后，设计了一个用于列车制动控制的PI闭环控制器，控制器的补偿输入为从速度观测器所获得的估计值。当列车速度观察器的状态收敛到近似列车系统的实际值时，控制器可以完全补偿动态摩擦力，大幅提高制动控制系统的控制性能。为了检测制动过程中的干扰故障，系统采用了一种基于测量速度和观察器速度估计的差值发生器，对两者差值进行滤波，如果滤波后的差值触发了检测阈值，就会认为出现制动故障，并通过禁用常规制动控制策略的方式来抑制故障。制动控制系统架构如图1所示。

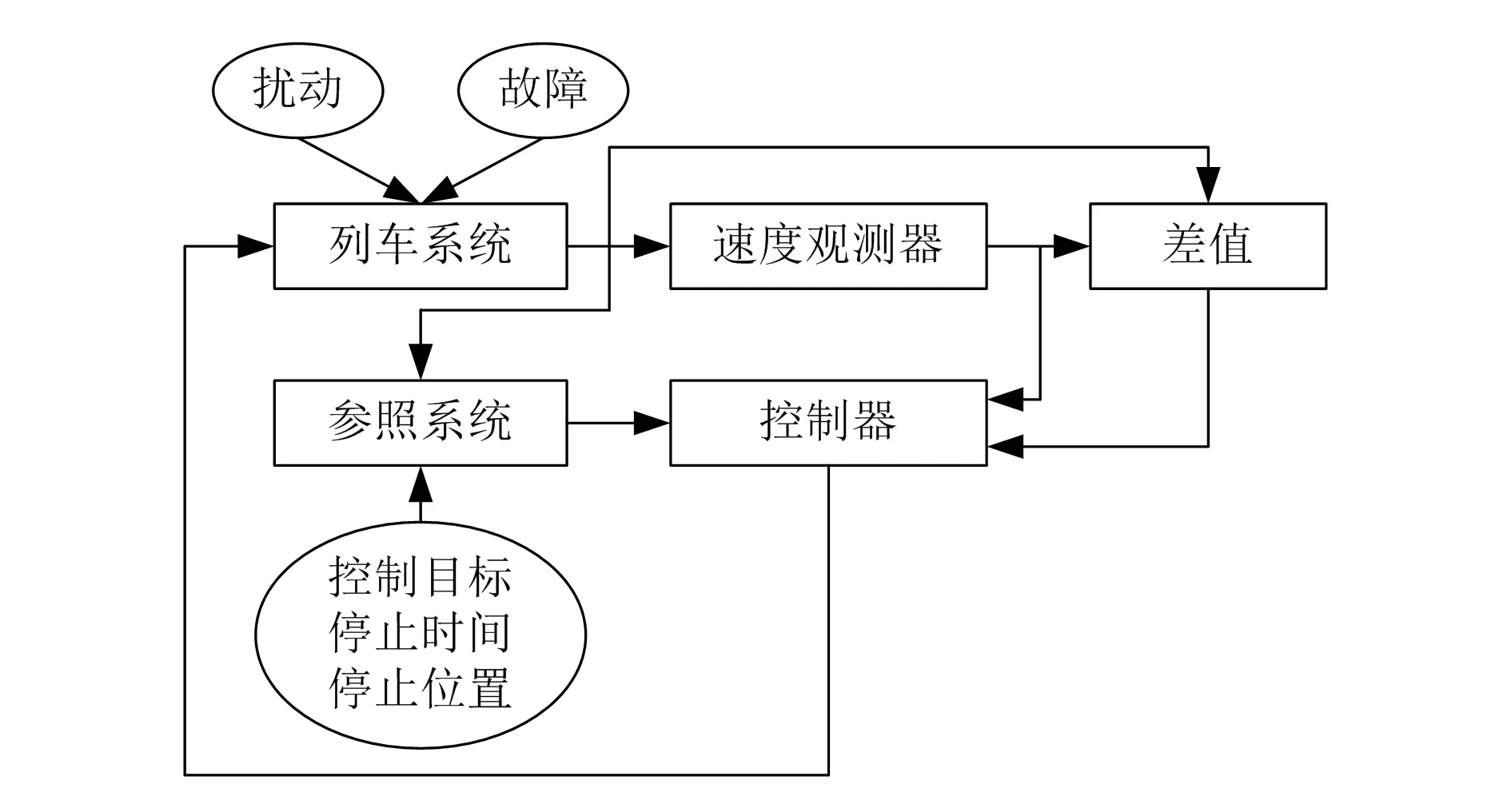
图1 列车制动控制系统架构

2 模型计算

2.1 控制器

对列车制动系统的控制器而言，理想化的列车参照系统提供了列车系统的最终停止位置以及推荐的制动幅度等目标值。

列车参照系统的运动方程为：

(8)

(9)

式中：t为制动过程的时间序列；t0为制动系统启动的初始时间；v(0)为在t0时刻列车的速度。从式(9)中推导出列车理想的停止时间和停止位置：

(10)

(11)

式中：vmin为列车停止前的最小速度，通常等于0；x(0)为在t0时刻列车所在的位置。基于式(9)对式(8)中的控制参数u*进行计算：

(12)

参照系统的控制参数u*以及相关参数依据列车的实际位置和速度进行更新，为制动系统提供目标控制值。

为了减少参照系统和列车实际系统之间的差值，基于u*对控制参数进行优化计算：

(13)

(14)

将式(13)代入式(14)，得出两种故障情况下的输入误差。

第一种是静态故障，其输入误差为：

(15)

第二种是动态故障，其输入误差为：

(16)

考虑到在误差过大的情形下进行误差补偿是不可行的，因此需要容错机制来保证制动系统的可靠性。该机制首先是禁用制动控制系统的功能，然后等到故障导致的误差降到故障检测阈值范围以内再启动制动控制系统。

2.2 观测器

为补偿制动系统的动态摩擦力，设计了一种基于无故障情况的输入观测器。

基于观测器的设计对列车运动方程进行修改：

(17)

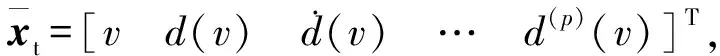
(18)

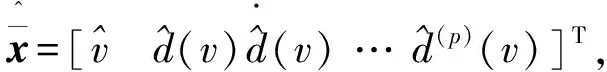
观测器的速度估算值与基于传感器的速度测量值的差值和确定的故障检测阈值是触发故障报警的根据。在实际系统中由于测量值的不确定性，因此需要采取一定的措施确保不会因测量误差而触发故障报警。故障检测阈值的确定是一个多约束的问题，即最小概率的假警报、最小概率的误报以及最快的检测速度。对实际应用而言，最快的检测速度下要能够检测出具有破坏影响的故障和可忽略、无关安全的检测数据偏差，以确保可以根据差值的大小推断出故障的影响程度，从而决定是否禁用自动制动控制系统。

3 仿真验证

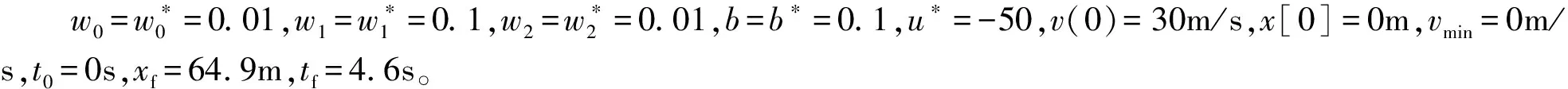
在无故障的情况下，列车停止位置的误差对比如图2所示。参照系统和仿真系统动态摩擦力的估计值d(v)的对比如图3所示，控制信号的对比如图4所示。

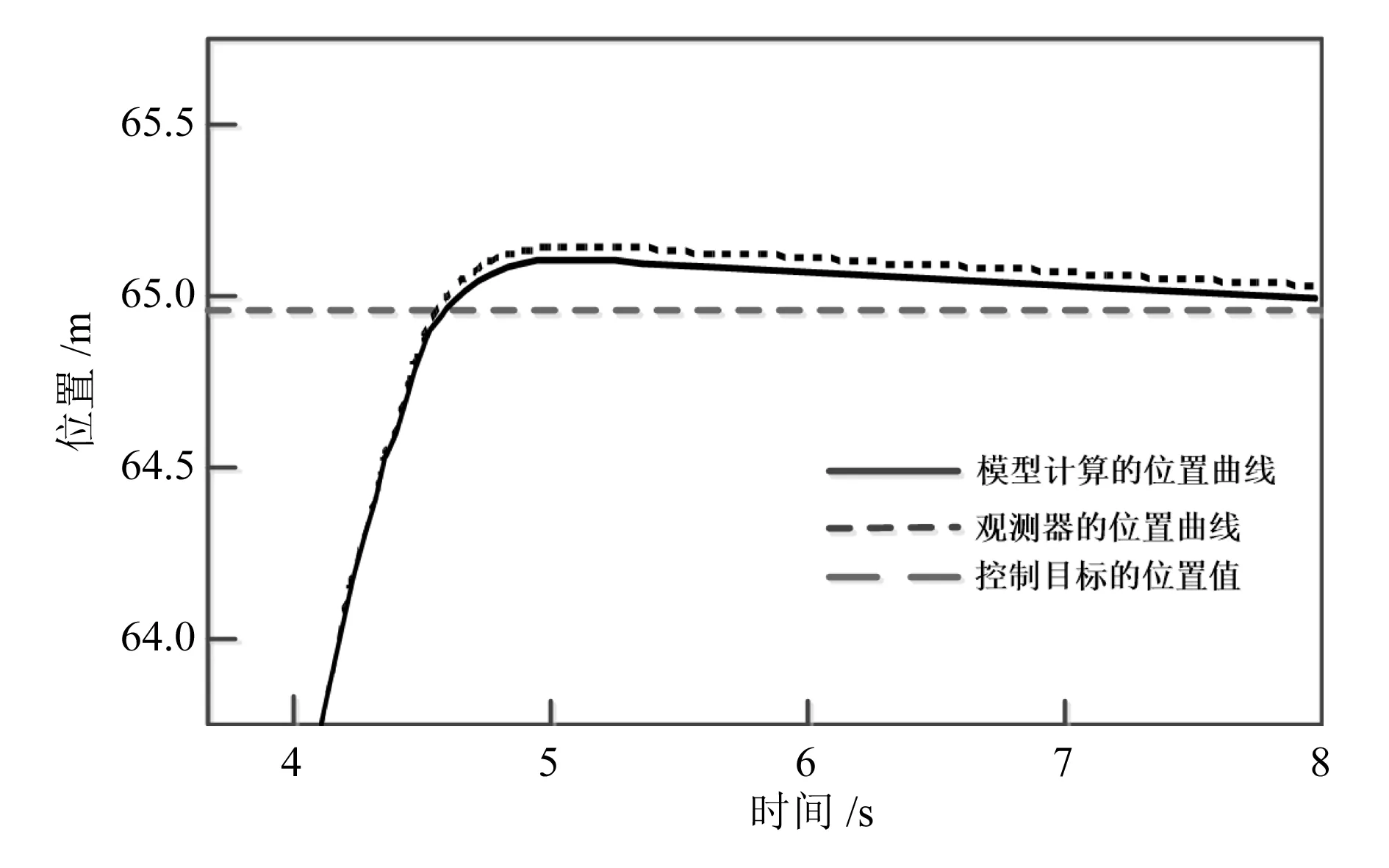
图2 无故障情况下列车的停止位置对比

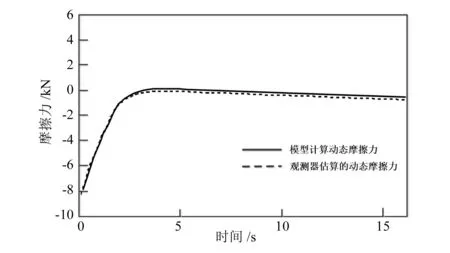
图3 无故障情况下的动态摩擦力对比

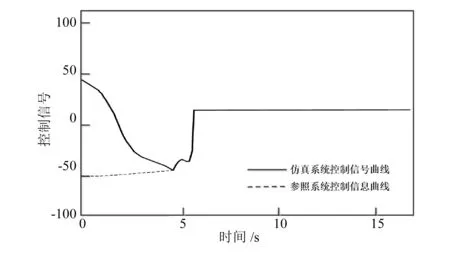
图4 无故障情况下的控制信号的对比

由图2可知，列车在参照系统和仿真系统中的停止位置误差为|x(tf)-xf|=0.061m，列车停止位置的精确度较高。图3中的d(v)估计值较为准确，而图4所示的控制信号曲线也较为平滑。

观测器的速度估算值与基于传感器的速度测量值差值曲线如图5所示。

图5 无故障情况下的速度差值曲线

由图5可知，由于没有故障扰动，经过短暂的波动之后差值快速收敛到零。

使用相同参数的仿真系统，在发生故障的情况下，采用本文所述的扰动补偿控制策略对列车的制动控制进行仿真测试，测试数据见表1。表中对不同的故障持续时间以及故障检测的时间延迟对最终位置误差εp=|x(tf)-xf|(ltrain)-1的影响进行了对比。测试中设定故障阈值为0.05，ltrain(列车长度)为100m。

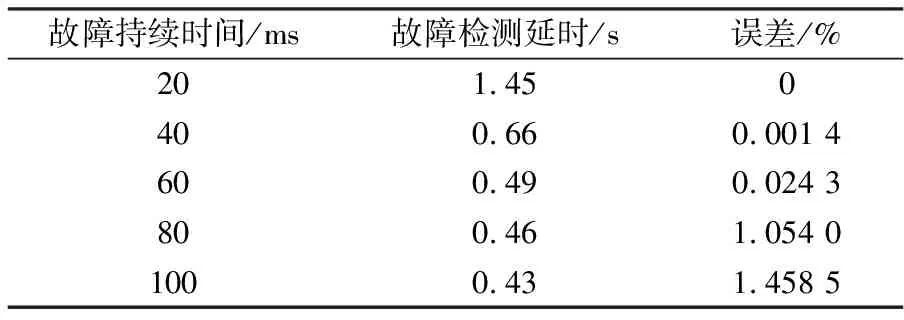
表1 不同故障持续时间的误差对比

故障持续时间为20ms时的位置误差对比曲线、控制信号曲线和速度差值曲线如图6～图8所示。

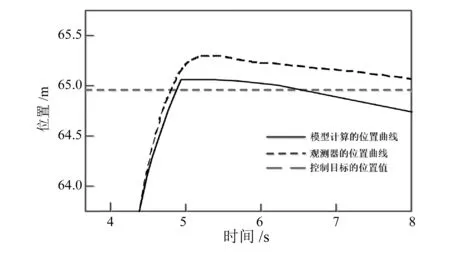
图6 故障持续时间为20ms的位置误差对比

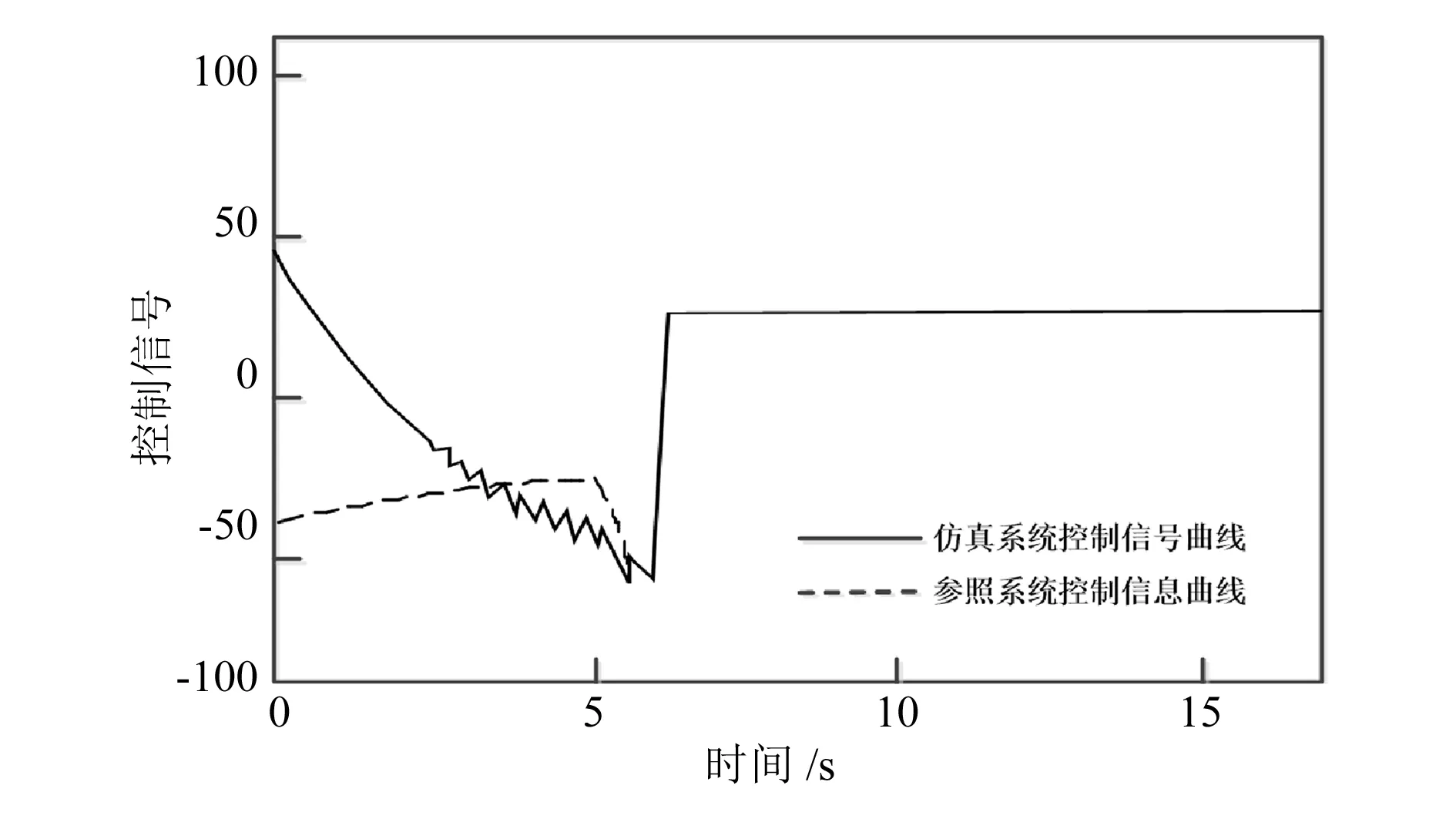
图7 故障持续时间为20ms的控制信号曲线对比

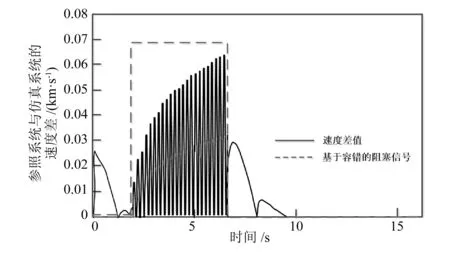
图8 故障持续时间为20ms的速度差值和故障容错曲线

由图6可以看出，在20ms的持续故障的扰动下，列车的停止位置误差只有0.01m。

故障持续时间为40ms时的控制信号曲线和速度差值曲线如图9、图10所示。

对比图7和图9，20ms持续故障扰动下的控制信号比40ms持续故障扰动下的控制信号具有更小的振荡幅度。由图8和图10 可知，在速度差值幅度过大时，容错机制开始发挥作用，自动制动控制系统被阻塞，直到差值降到阈值以下，自动制动控制系统才开始工作。

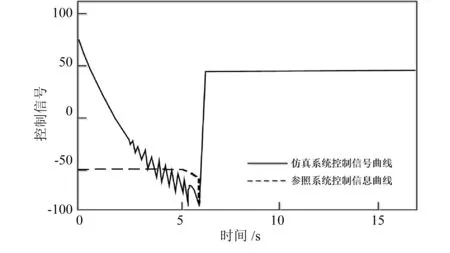
图9 故障持续时间为40ms时的控制信号曲线对比

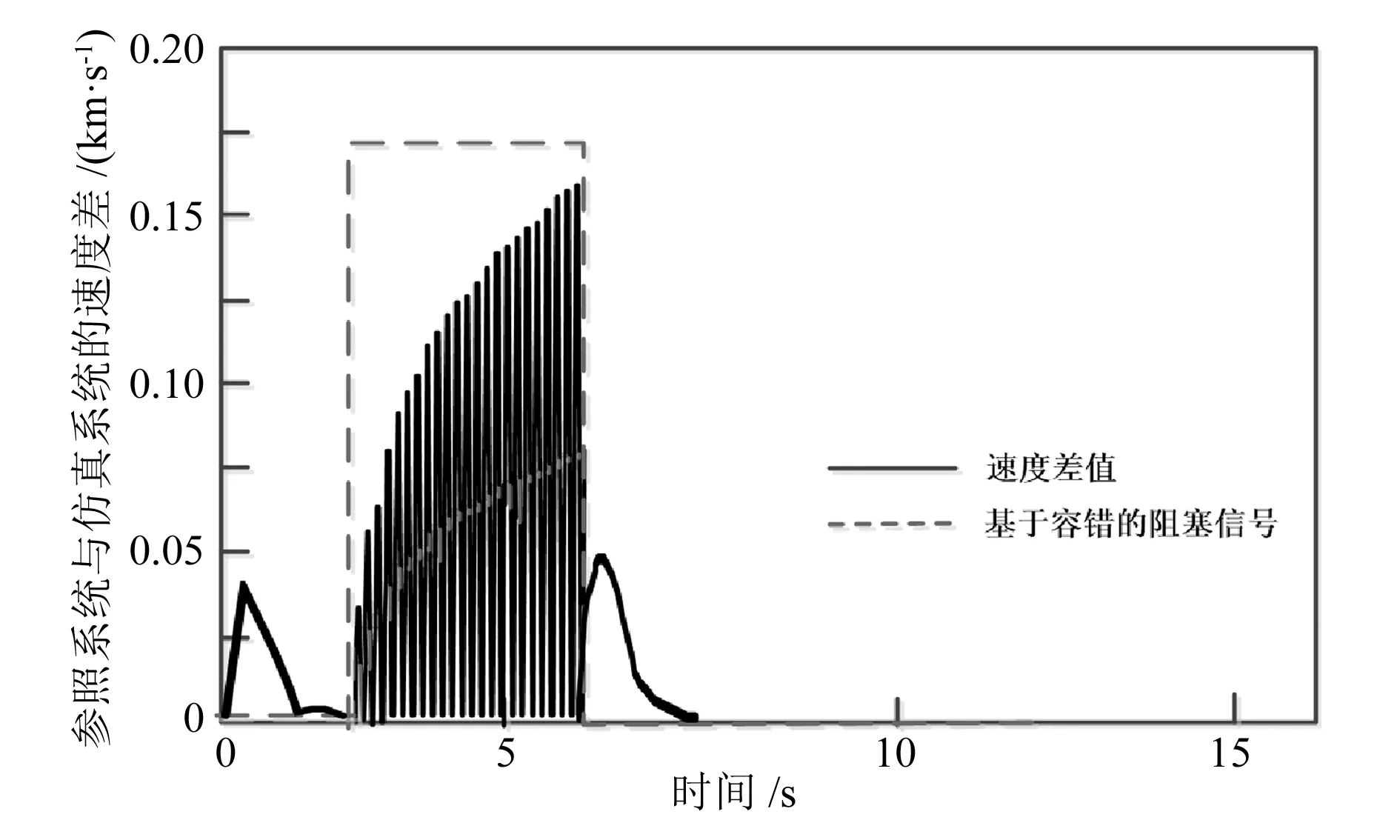
图10 故障持续时间为40ms时

4 结束语

本文提出了一种具有较好抗干扰性能和容错机制的列车制动控制系统模型。该模型包括故障检测、扰动补偿和容错机制，对模型估算值和速度测量值的不确定性具有良好的鲁棒性。通过仿真分析表明，该模型在不同故障持续时间和不同故障检测延时情况下，都具有良好的制动性能。