基于非线性短时傅里叶变换阶次跟踪的变速行星齿轮箱故障诊断
2018-09-22王友仁黄海安
王友仁 王 俊 黄海安
南京航空航天大学自动化学院,南京,211106
0 引言
行星齿轮箱广泛用于直升机主减速器、风力发电机组等。行星齿轮箱常工作在复杂多变的环境下,其太阳轮、行星轮、齿圈等部件的故障发生概率高、易损坏[1]。行星齿轮箱发生故障时,振动信号的故障特征微弱、非平稳、有噪声与干扰,不仅受故障、多个传递路径引起的调频、调幅和调相作用,还受到转速变化引起的调制、多个激励振动源之间相互耦合作用,使得传统的信号频谱分析技术难以提取有效故障特征[2]。
变转速下旋转机械振动信号分析主要采用无键相阶次跟踪方法(non⁃bonding phase order tracking method,NPOTT),通过角度域等间隔采样技术将时间域的非平稳信号转化为角度域的平稳或循环平稳信号,消除转速波动带来的频率模糊现象。李蓉等[3]提出基于线调频小波路径追踪(chirplet path pursuit,CPP)算法[4]与总体平均经验模态分解(ensemble empirical mode decomposi⁃tion,EEMD)的齿轮箱复合故障诊断方法,用CPP算法得到振动信号的转频曲线,对转频信息重采样并进行EEMD分解,获得了变转速齿轮箱复合故障特征,但CPP算法复杂、效率低。RODOPOULOS等[5]提出基于谐波信号分解的瞬时转速估计方法,将瞬时转速估计问题转化为信号模型特征值求取问题,但该方法对噪声敏感,不适用于强噪声情况下的瞬时转速估计。郭瑜等[6]提出一种基于瞬时频率(instantaneous frequency,IF)估计的旋转机械阶次跟踪方法,利用短时傅里叶变换(short⁃time Fourier transform,STFT)谱峰值进行振动信号瞬时频率估计,该方法在瞬时频率变化较小情况下结果较好,但不适用于瞬时频率变化剧烈的情况。非线性短时傅里叶变换(non⁃liner short⁃time Fouri⁃er transform,NLSTFT)方法[7]能准确估计振动信号瞬时频率,对瞬时频率曲线积分获得瞬时相位曲线,通过重采样完成阶次跟踪过程。NLSTFT方法在大转速变化、强噪声情况下效果较好,值得进一步深入研究。
变分模态分解(variational mode decomposi⁃tion,VMD)[8]是一种新的非平稳信号自适应分解方法,相比于 EEMD、LMD[9]和 EWT[10]等传统信号分解方法,VMD不存在模态混叠且能分解出频率相近成分。然而,VMD算法有两个不足之处:①模态分解结果受到二次惩罚参数α和模态个数K影响,难以选择合适的数值;②当噪声方差超过一定阈值时,VMD算法可能会失效。为此,本文设计一种改进型VMD信号分解方法,采用粒子群优化(particle swarm optimization,PSO)[11]算法进行全局优化,确定参数α和K,并在VMD信号分解前基于非凸重叠组收缩(non⁃convex overlapping group shrinkage,NCOGS)[12]算法进行信号降噪处理,提高信噪比,提取有效的故障特征信息。
针对噪声情况下大转速变化行星齿轮箱故障诊断问题,本文提出一种基于NLSTFT阶次跟踪和带前置降噪自适应变分模态分解的行星齿轮箱故障诊断方法。通过NLSTFT无键相阶次跟踪消除振动信号的变转速频率模糊现象,利用NCOGS算法降低信号噪声,进行VMD自适应模态分解,提取各模态分量信号包络谱特征频率进行故障诊断。
1 振动信号瞬时频率估计与阶次跟踪
NLSTFT是一种新型的非平稳信号时频分析方法,它在STFT基础上额外引入一个时变解调算子,用于解决调制成分带来的时频聚集性不高、时频能量发散问题,可用于信号瞬时频率估计。
根据Ville对瞬时频率的定义:瞬时频率等于信号瞬时相位的导数。考虑一输入信号x(t),基于Hilbert变换构造的解析信号可以表示为
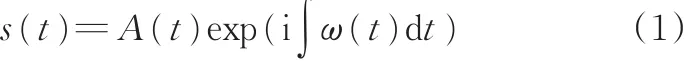
式中,s(t)为x(t)的解析信号;A(t)为幅值;ω(t)为解析信号的瞬时频率。
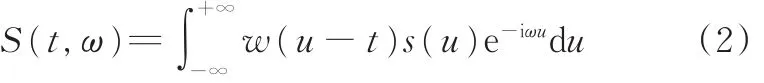
由于信号中有较强的调制成分e-iωu,瞬时频率的STFT幅值会小于谐波幅值,导致时频谱模糊,且瞬时频率在时频谱上会出现时频扩散现象,时频分辨率不高。为了消除调制成分带来的负面影响,NLSTFT算法在STFT基础上,乘以一个额外的时变解调算子e-ic(t)(u-t)2/2,具体表达式为
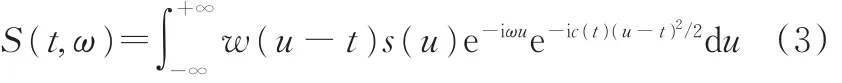
标准STFT的表达式为
其中,c(t)是瞬时频率的一阶导数。
如果解调算子和调制成分一致,则可以彻底消除调制影响,瞬时频率幅值能够达到最大化,使得时频谱上的时频聚集度及时频分辨率高。
实际情况中,一般不知道瞬时频率变化规律,c(t)的值也未知。本算法采用递归策略,在第一次计算 NLSTFT 时 c(t)=0,即 NLSTFT 退化为STFT算法。进行信号时频谱分析后,利用频域峰值搜索算法得到对应时刻t的峰值数据P(t),并通过4阶多项式拟合P(t)曲线得到瞬时频率估计曲线I(t),然后把I(t)的一阶导数作为第二次迭代时c(t)的值。由此,依次进行迭代运算,直到瞬时频率曲线没有明显改变为止。以第n次与第n-1次迭代获得的瞬时频率曲线I(t)之间的平均误差ξ作为迭代终止条件:
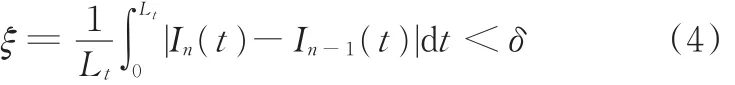
其中,In(t)、In-1(t)分别是第n次和第n-1次迭代计算得到的瞬时频率估计值,一般选取δ=0.05。Lt为In(t)曲线时间长度,例如Lt=1 s。
利用NLSTFT得到估计瞬时频率曲线后,对瞬时频率求积分可得瞬时相位曲线,然后利用瞬时相位信息进行振动信号重采样,将与转速有关的非平稳时域信号转化为与转速无关的平稳角域信号,完成无键相阶次跟踪过程。阶次跟踪算法流程如图1所示。
NLSTFT算法具有复杂度低、运算速度快、精度高等优点,NLSTFT瞬时频率估计精度高和抗噪能力好,能有效提高阶次跟踪精度和效率。
2 变分模态信号分解与故障诊断
VMD将信号分解过程转化为通过迭代搜寻变分模型最优解,使得每个模态估计带宽之和最小。VMD算法对本征模态函数(intrinsic mode function,IMF)进行了重新定义,它是一个调幅-调频信号:
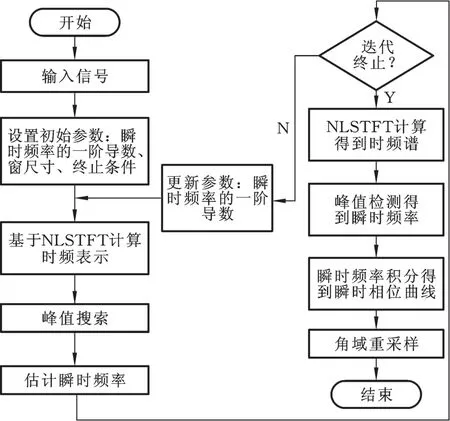
图1 NLSTFT无键相阶次跟踪算法流程图Fig.1 Flow chart of NLSTFT non-bonding phase order tracking algorithm
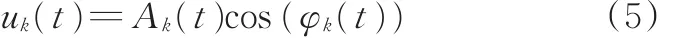
其中,Ak(t)为瞬时幅值;φk(t)为非单调递减的瞬时相位;k表示第k个模态,k=1,2,…,K。
通过 φk(t)对 t求导,可得瞬时频率 ωk(t)=φ˙k(t)。Ak(t)和ωk(t)相对于φk(t)来说变化非常缓慢,即在一段较长的时间间隔[t-δ,t+δ ]内,δ ≈ 2π φ˙k(t),uk(t)可看作是幅值 Ak(t)、相位φk(t)的谐波信号。VMD自适应模态分解过程是变分问题求解过程,包括变分问题构造和变分问题求解两部分。
2.1 变分问题构造
变分问题可以描述为寻求K个模态函数uk(t),使得每个模态的估计带宽之和最小,约束条件为各模态之和等于输入信号x(t),其中,带宽的定义为
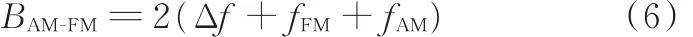
其中,Δ f为瞬时频率的最大偏差;fFM为瞬时频率的偏移率;fAM为Ak(t)的最高频率。具体构造过程如下:
(1)计算模态分量uk(t)的解析信号,通过Hil⁃bert变换得到单边频谱;
(2)通过指数修正,将一个预估中心频率混合到解析信号中,使得每个模态分量的单边频率调制到各自估算的中心频率处;
(3)估计各模态信号带宽,使其带宽之和最小:
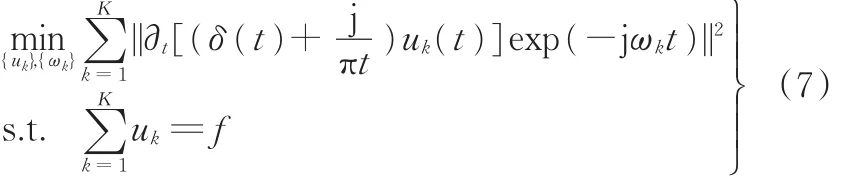
其中,{uk}:={u1,u2,…,uk}为各模态函数集合,{ωk}:={ω1,ω2,…,ωk}为各中心频率集合,∂t表示函数对t求偏导。
2.2 变分问题求解
式(7)所示的优化问题是带约束的变分问题,引入二次惩罚因子α和拉格朗日乘积算子λ,将约束变分问题转化为无约束变分问题,修改后的表达式为
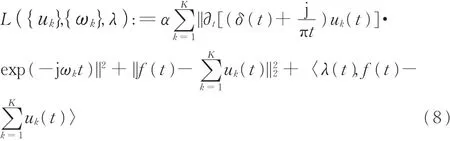
其中,f(t)为原始信号的频域表示。
利用交替方向乘积算子(alternate direction method of multipliers,ADMM)可以求解上述变分问题。VMD算法实现步骤如下:
(2)更新所有模态信号,即
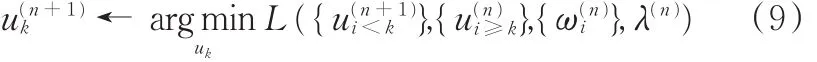
(3)更新所有模态信号的中心频率,即
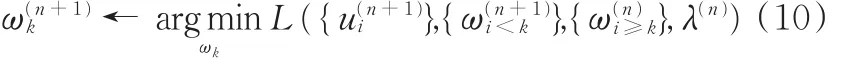
(4)更新λ
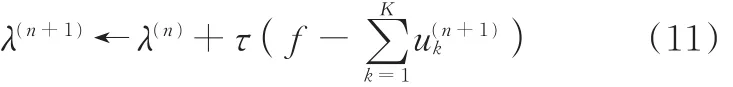
其中,τ为噪声容限参数,可以设定为0。
(5)重复步骤(2)~(4),直到满足收敛条件为止。收敛条件:
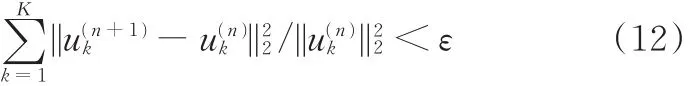
2.3 VMD算法改进
VMD算法分解结果受到二次惩罚参数α和模态个数K影响。α越小,计算得到的各个IMF分量的带宽越大,则各个IMF分量中噪声就越多,且各IMF成分间可能出现交叉。α越大,各个IMF分量的带宽越小,可能会出现中心频率偏移,导致模态分解错误。模态个数K决定中心频率个数,K选取过小,模态分量间会出现混叠;K选取过大,则会导致某个模态分解分布在多个模态中,增加了计算时间,且会产生虚假分量。
VMD算法在低噪声情况下信号分解鲁棒性较好[13],例如,当噪声方差为0.005时,可以达到100%的分解成功率,而当噪声方差大于0.1时,分解成功率降为0,算法就不收敛,无法正确分解信号。
针对VMD算法的上述不足,本文采用PSO算法全局寻优确定K和α,且在VMD分解前,采用NCOGS算法进行信号降噪,减小噪声方差,解决VMD失效问题。
2.3.1 VMD参数优选
当行星齿轮箱出现故障时,振动信号会呈现冲击调制特性。若某个IMF分量中包含故障敏感信息,其波形中会有相应的冲击脉冲,此时IMF分量包络熵值较小,则将包络谱熵作为PSO算法的适应度函数,实现全局寻优参数K和α。
2.3.2 NCOGS降噪算法
NCOGS是一种利用信号组稀疏特性的平移不变收缩算法,利用信号成组稀疏性将降噪问题转化为凸优化问题,算法计算效率高。
假定信号表达式为

其中,y(i)是含噪检测信号,i∈ I={0,1,…,N-1};N为信号点数;x(i)是不含噪声的原始信号且已知具有组特性(即大幅值系数以组形式存在);η为高斯加性噪声。
将上述信号降噪问题转化成最优化问题:
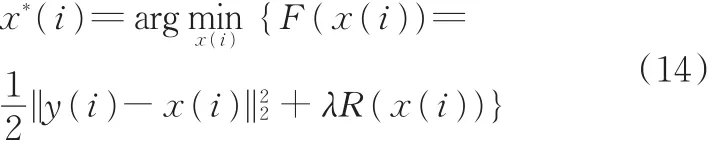
定义罚函数为
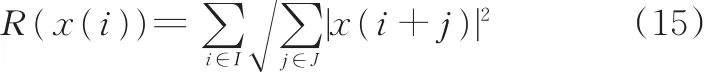
其中,j={0,1,…,J-1},J为组个数。
代价函数转化为
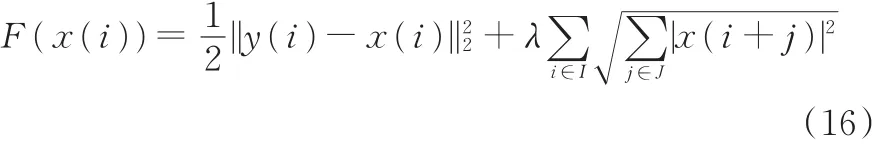
式(16)中,目标函数、罚函数都是严格凸函数,能利用受控极小化算法进行求解。
2.4 故障诊断算法
设计一种基于NLSTFT无键相阶次跟踪和带前置降噪VMD分解的行星齿轮箱故障诊断方法,算法实现过程如下:
(1)采用NLSTFT精确估计瞬时频率,对瞬时频率曲线进行积分,转化为瞬时相位曲线,利用瞬时相位信息进行角域重采样完成阶次跟踪过程,输出角域信号;
(2)利用NCOGS算法进行角域信号降噪;
(3)用PSO算法优化确定模态个数K和二次惩罚参数α。对降噪的角域信号进行VMD自适应模态分解,获得K个模态分量信号;
(4)依据包络谱熵选取对故障敏感的IMF分量,并对其进行包络谱解调分析,获得故障特征频率。进而分析与正常状态信号包络谱特征频率的差别,实现故障诊断。
3 仿真结果分析
3.1 仿真信号
当行星齿轮箱发生局部损伤故障时,振动信号中有以啮合频率为载波频率、齿轮转频及其倍频为调制频率的稳态调频信号,同时还存在周期性冲击调幅信号[14]。
根据振动信号特点,构造以下仿真信号:
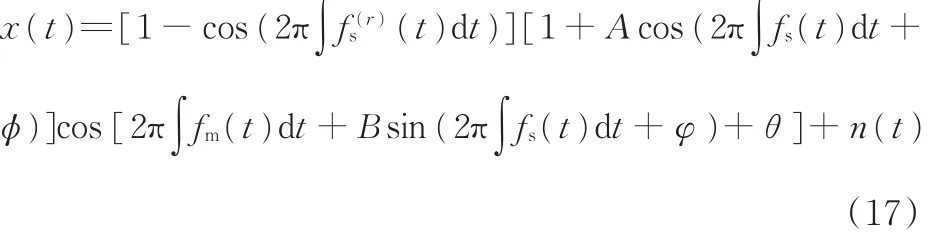
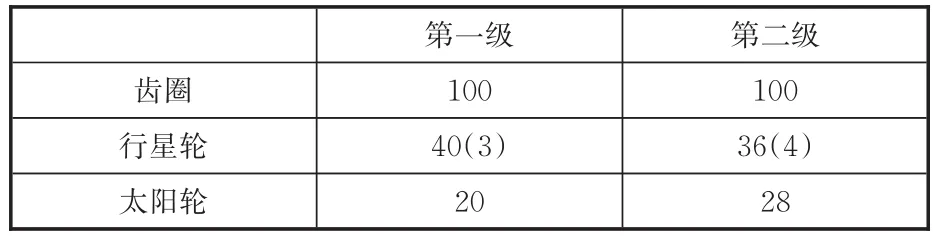
表1 行星齿轮箱参数中齿轮的齿数Tab.1 Number of gear teeth in planetary gearbox
图2所示分别为仿真信号波形、频谱与时频谱,由图2b可知,转速变化导致频谱图中频率模糊现象,而且啮合频率及其边频出现混淆,容易误诊。
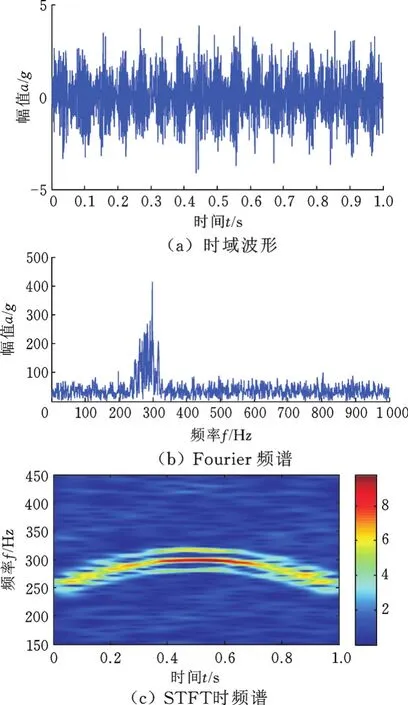
图2 仿真信号波形及时频谱Fig.2 The waveform and time-frequency spectrum of simulated signal
3.2 阶次跟踪
图3 为NLSTFT对仿真信号第一次迭代运算得到的瞬时频率曲线,因第一次迭代时缺少先验知识,故设置解调算子c(t)=0,该算法退化为ST⁃FT,此时瞬时频率估计有较大偏差。
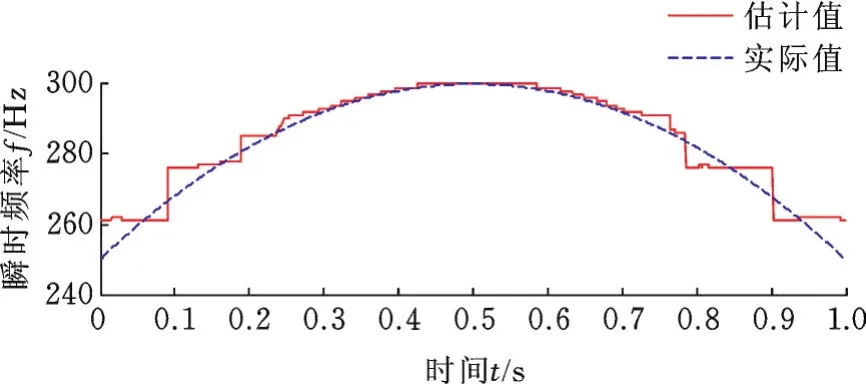
图3 第一次迭代得到的瞬时频率曲线Fig.3 IF curve obtained in the first iteration
由图4可知,由于第二次迭代使用了第一次迭代得到的瞬时频率先验信息,故能大幅改善瞬时频率估计精度。
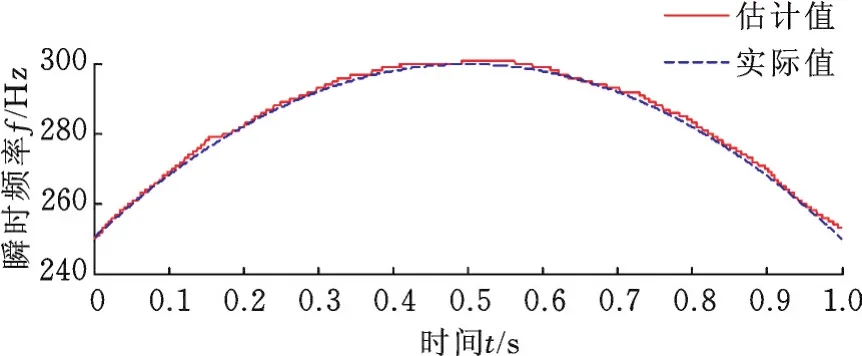
图4 第二次迭代得到的瞬时频率曲线Fig.4 IF curve obtained in the second iteration
迭代终止发生在第4次迭代,如图5所示。经过4次迭代后得到了精确的瞬时频率曲线,且时频分辨率大幅提高。
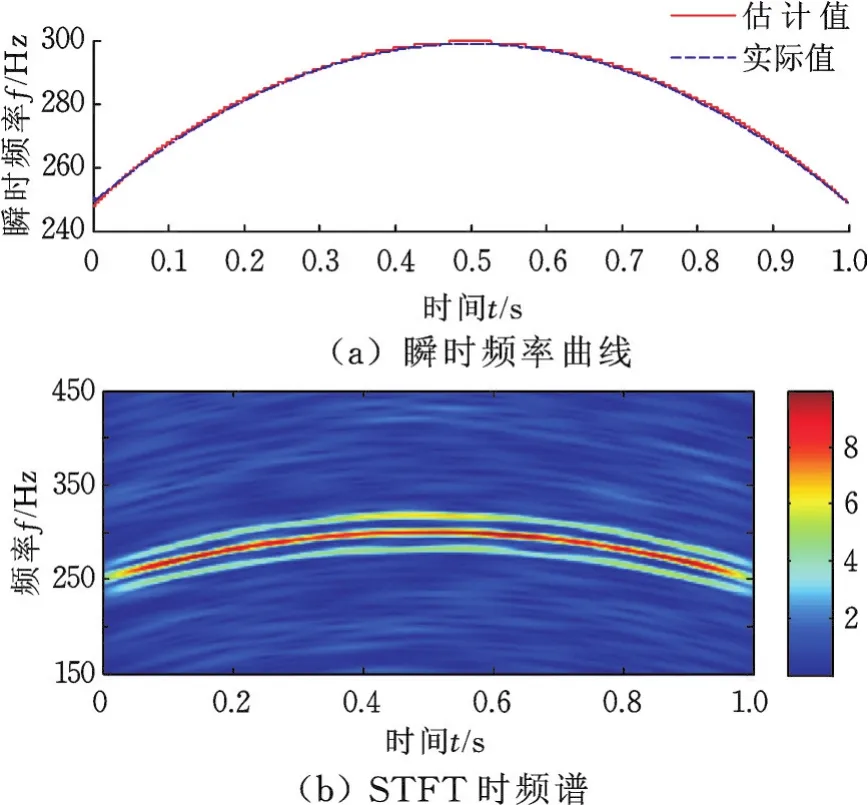
图5 第四次迭代Fig.5 The fourth iteration
将本方法与阶次跟踪中应用广泛的瞬时频率估计算法CPP进行对比。CPP参数设置为:动态时间支撑区设置为5,在路径连接后,使用4阶多项式对各区间曲线拟合。由图6可知,CPP算法可以得到瞬时频率曲线,但存在一定的瞬时频率估计误差,即使增加动态时间支撑区长度,效果改善程度也有限。
为验证本文所提阶次跟踪方法的优越性,选择CPP和STFT算法进行对比分析。由图7可知:NLSTFT算法的相对误差小于0.5%,明显优于CPP和STFT算法的瞬时频率估计精度。
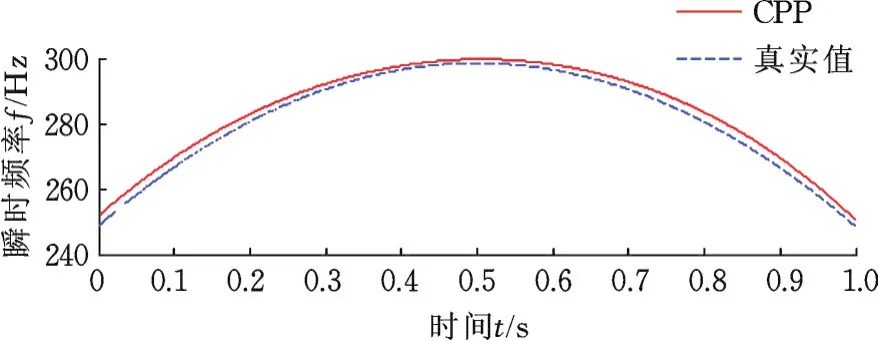
图6 CPP估计瞬时频率曲线Fig.6 IF curve estimated by CPP
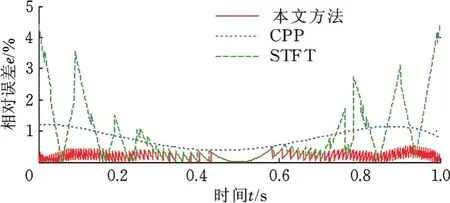
图7 三种方法对比Fig.7 Comparison of three IF estimation methods in relative error
表2所示为三种算法运行时间的结果,其中仿真运行环境为:MATLAB 2013a,CPU为i7⁃6700的8核处理器,主频为3.4 GHZ,内存为16 GB。可以看出,本文算法运行时间远低于CPP算法。

表2 三种算法运行时间Tab.2 Comparison of three methods in running time
利用NLSTFT算法得到瞬时频率曲线后,通过积分计算得到瞬时相位,再通过重采样转换为角域信号,完成阶次跟踪过程。图8为阶次跟踪后的谱图,可发现频率模糊现象和时频聚集性明显改善。
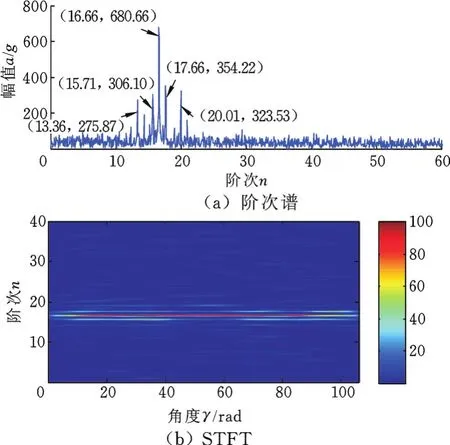
图8 阶次跟踪后信号谱图Fig.8 Signal spectra after order tracking
进一步评估本文算法的噪声鲁棒性,分析不同信噪比条件下的计算测量值和真实值的均方根误差,如图9所示,可以看出:在一定的噪声范围内,本文方法的均方根误差均小于CPP和STFT算法,抗噪声能力较强。
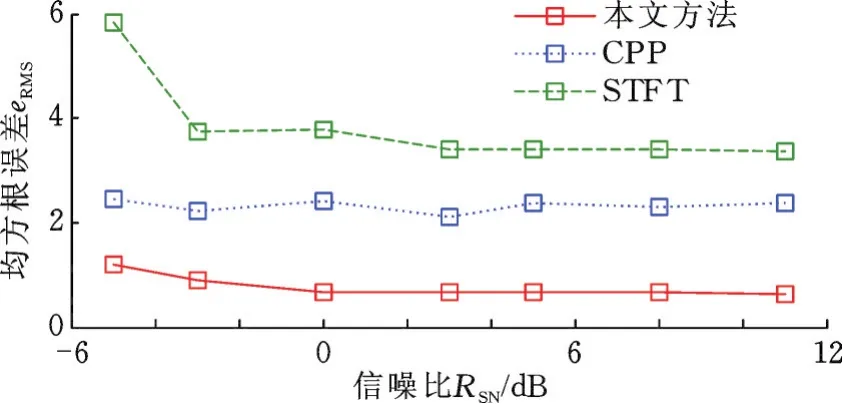
图9 噪声对瞬时频率估计的影响Fig.9 The effect of noise on the IF estimation
3.3 信号分解
经过阶次跟踪消除转速波动影响后,采用VMD自适应模态分解法分离故障信号,利用PSO算法确定VMD的参数K和α,为了避免在噪声情况下VMD失效,采用NCOGS算法进行滤波去噪。
图10所示为对角域加噪信号进行NCOGS滤波处理结果,NCOGS能有效去除加性噪声,提高信噪比。
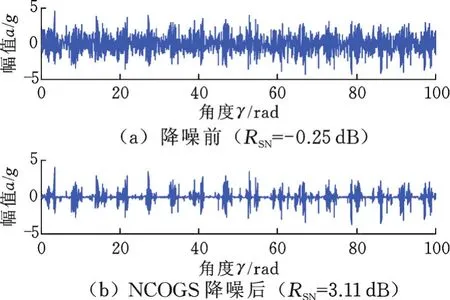
图10 NCOGS降噪前后角域图Fig.10 Angular domain waveform before and afterNCOGS de-noising method
对NCOGS降噪后的角域信号进行VMD分解,由PSO算法得到参数K=3,α=2 050。VMD将原始信号分解为3个模态分量,如图11、图12所示。模态分量2包含故障信息,对其进行包络谱分析,得到故障特征频率,如图13所示。其中,太阳轮局部故障特征频率fs=3.33阶幅值远大于其他阶次幅值,可正确识别太阳轮局部故障,验证了本文算法有效性。
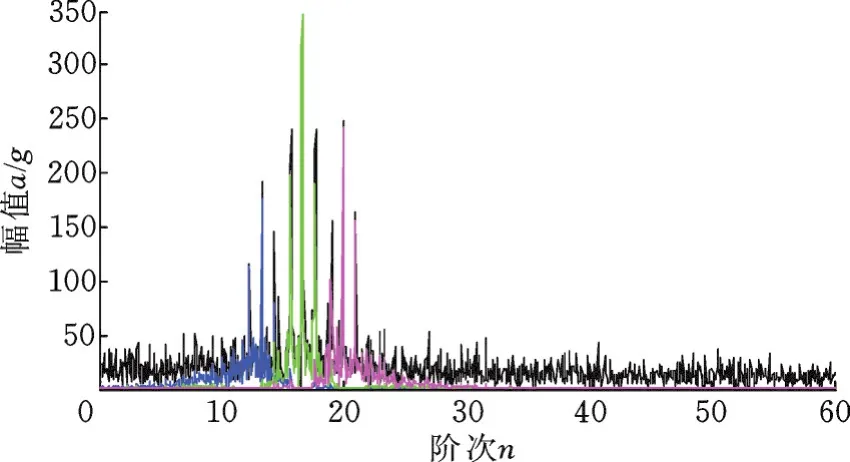
图11 VMD分解得到三个模态分量Fig.11 Three IMFs obtained by VMD
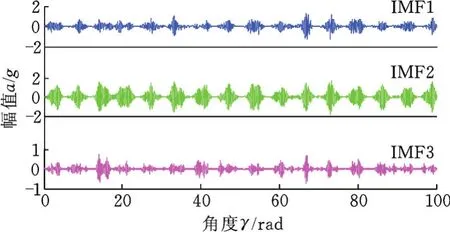
图12 各模态分量Fig.12 Each component of IMFs
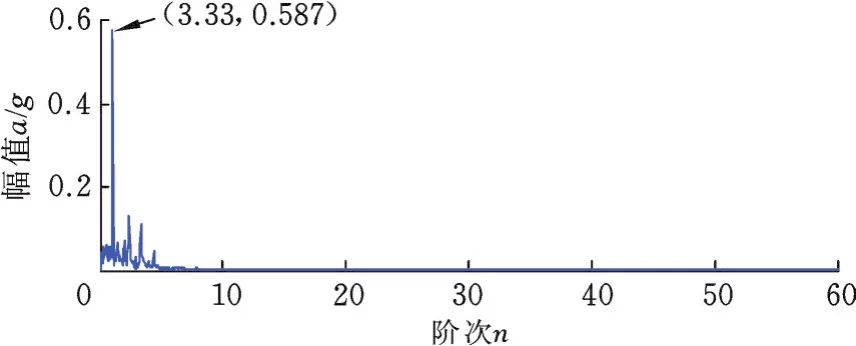
图13 模态分量2包络谱Fig.13 Envelop spectrum of the second IMF
4 实验结果分析
4.1 实验平台与模拟故障
图14所示为行星齿轮箱故障诊断综合实验台,由驱动电机、可编程控制面板、传动齿轮箱、磁粉制动器、加速度传感器、转速传感器、数据采集器等组成。行星齿轮箱参数见表1。实验中模拟故障为太阳轮切齿故障,故障位置在第二级太阳轮,如图15所示。第2级行星齿轮箱输出轴承所受的负荷为40 N·m,转速变化范围是2400~3600 r/min。加速度传感器安装在行星齿轮箱箱体上,振动信号采样频率为10 kHz,采样时间为3 min。

图14 行星齿轮箱故障诊断实验平台Fig.14 Experiment platform for fault diagnosis of planetary gearboxes
根据行星齿轮箱参数,计算出相应的啮合频率和故障特征频率,如表3所示。其中,驱动电机旋转频率

图15 太阳轮切齿故障Fig.15 Chipped tooth of sun gear
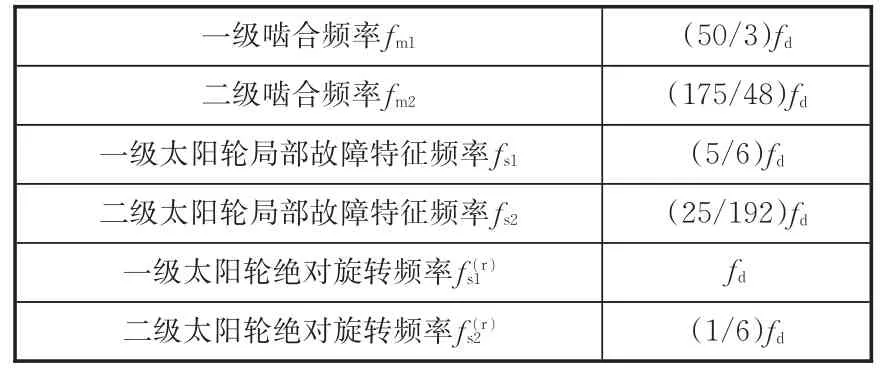
表3 行星齿轮箱有关特征频率Tab.3 Characteristic frequency of planetary gearbox
4.2 振动信号分解与故障诊断结果分析
振动信号时域图和频谱图见图16。由图16b可知,因二级啮合频率过低且离传感器较远,导致被一级啮合频率完全被覆盖。同时,转速波动引起Fourier频谱出现左右漂移现象,难以准确分析时频变化规律,故障容易误诊。
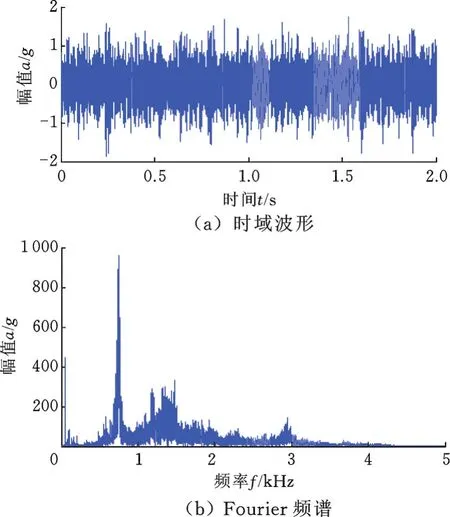
图16 振动信号时域图和频谱图Fig.16 Vibration signals under the sun gearfault condition
图17 为NLSTFT阶次跟踪估计得到的转速曲线。图18所示为本文算法阶次跟踪后的阶次谱,可看出,较好地消除了频率漂移现象,频率成分以fm1及其谐波、f(r)s1及其倍频成分为主,而二阶啮合频率被掩盖。
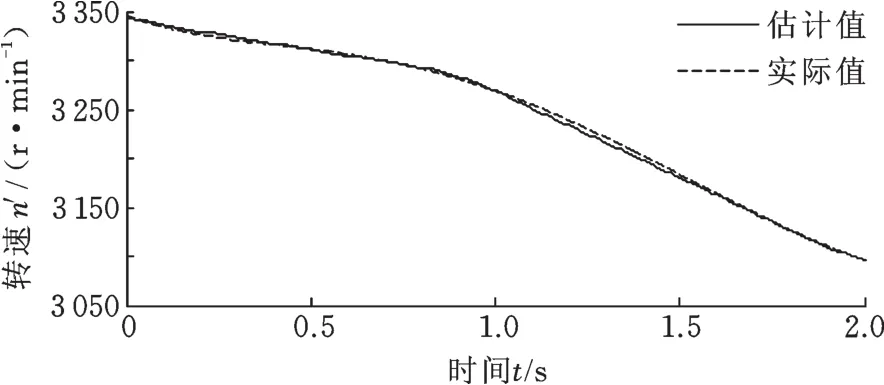
图17 NLSTFT估计转速信号Fig.17 Speed signal estimated by NLSTFT
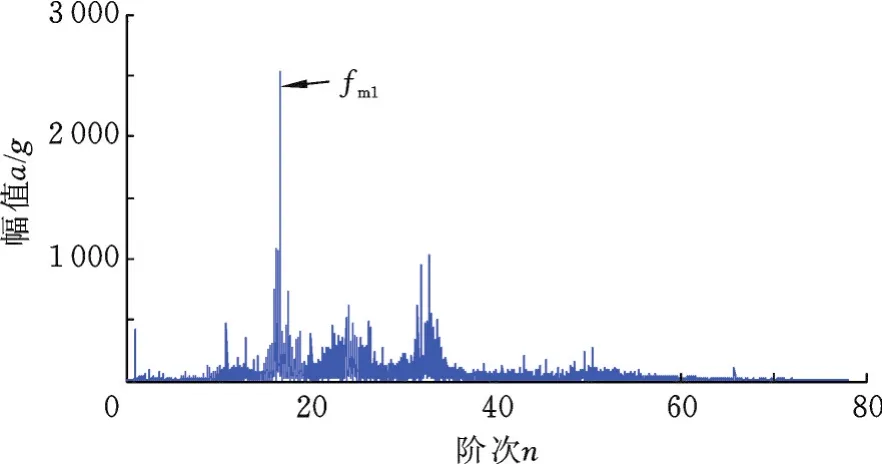
图18 NLSTFT获得的阶次谱Fig.18 Order spectrum obtained by NLSTFT algorithm
将NLSTFT阶次跟踪法与STFT和CPP法进行比较。由表4可知,NLSTFT算法的瞬时频率估计相对误差小于0.6%,优于STFT算法,且运行时间与STFT算法接近,而CPP算法运行时间相对较长。证明了NLSTFT算法的瞬时频率估计精度高、计算复杂度较低。

表4 三种瞬时频率估计算法比较Tab.4 Comparison of three IF estimation methods
因第二级行星齿轮系和特征频率集中在低频部分,在故障诊断前,需要去除一级行星齿轮系的影响,故对角域信号进行低通滤波,只分析[0,10]阶频段内信号。图19a所示为滤波后角域信号由VMD分解获得的3个模态分量,PSO算法得到优化参数K=3,α=2 075。为提取故障特征,对3个模态分量均进行包络谱分析,发现模态分量2包含了故障信息,如图19b所示。由表3可知,太阳轮局部故障特征频率fs2=0.44 Hz。由图19b可知,故障特征频率fs2阶处幅值明显大于其他频率成分,很容易判断出现了太阳轮局部故障,诊断结果与实际情况相符合。
5 结论
(1)给出了一种NLSTFT无键相阶次跟踪算法,新算法的时频聚集性好、计算复杂度低,适用于转速变化大、噪声强情况下振动信号瞬时频率估计和无键相阶次跟踪。
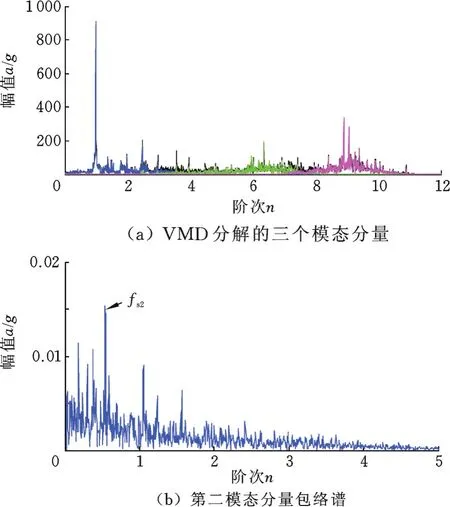
图19 VMD分解模态分量Fig.19 IMFs obtained by VMD algorithm
(2)设计了基于PSO的VMD模态分解算法,并采用非凸重叠组收缩算法进行角域信号滤波降噪,避免了噪声情况下VMD模态分解失效。
(3)提出了一种基于NLSTFT无键相阶次跟踪和粒子群优化VMD模态分解的行星齿轮箱故障诊断方法,提高了变转速与噪声情况下行星齿轮箱故障诊断性能。
