一种基于神经网络的双足机器人混合动力学系统辨识方法

吴晓光 张天赐 韦 磊 李艳会 王挺进 张 波

1.燕山大学河北省测试计量技术及仪器重点实验室，秦皇岛，066004 2.中国唐山机车车辆有限公司，唐山，063000

0 引言

随着双足机器人技术的发展，高效、稳定、准确的控制策略已成为双足机器人研究中的重要方向，多种行之有效的控制方法相继被提出［1⁃4］，然而上述方法大多建立在机器人系统已知的基础上。双足机器人自身固有的变结构、强耦合特性［5］，以及足地碰撞引发的连续与离散混合特性［6］，使得准确建立模型变得非常困难。实现双足机器人的高效稳定控制，需要构造一个确定的非线性映射来代替原系统，即双足机器人系统辨识。因此，辨识技术成为机器人不确定系统高效控制中亟待解决的关键问题。

为将系统辨识技术有效地应用于双足机器人的高效控制，研究人员尝试了多种适宜于复杂非线性系统的辨识方法，如采用最小二乘法［7］、支持向量机［8］、神经网络［9］来辨识双足机器人的运动轨迹。在各类型神经网络中，径向基函数神经网络（radial basis function neural network，RBFNN）以其强大的非线性函数逼近能力、自学习适应能力，受到众多学者的青睐。CAPI等［10］针对不同任务下机器人步态的具体要求，利用RBFNN实现了运动轨迹的辨识，并成功应用于双足机器人确定步态的行走控制。CHALODHORN等［11］利用RBFNN辨识双足机器人的逆动力学模型，并基于该辨识模型预测给定位姿下的最优关节转矩，从而实现机器人的稳定行走。然而，上述研究所采用的辨识方法仅针对主动机器人的连续运动轨迹而忽略了足地接触碰撞的影响，不能充分表征双足机器人动力学本质；摒弃了运动过程中步态的多样性，不适用于步态柔顺、自然的混合动力学机器人系统。因此有必要引入一种有效的、针对离散足地碰撞的建模方法作为上述研究的补充，将二者有机结合，实现对双足机器人动力学本质的更深层次表达。

动态模糊神经网络（dynamic fuzzy neural network，DFNN）是目前常用的离散系统建模工具之一。DFNN作为一种改进的模糊神经网络，具有强大的泛化能力与对动态系统的在线辨识与预测能力［12⁃13］。WU等［14］设计一种 DFNN并应用于非线性离散时间序列的辨识。徐春梅等［15］利用学习速率自适应调整的DFNN，成功实现了动态非线性离散系统的快速辨识与准确预测。因此，可以利用基于DFNN的离散建模方法，对足地碰撞阶段进行准确的辨识。此外，混沌步态作为双足步行中的最为复杂步态表现形式，不仅具有深层次的复杂特性，同时蕴含着深层次的系统动力学特性［16］，因而可将双足机器人系统的混沌步态作为辨识目标，以充分体现双足机器人混合系统的动力学特性。

本文针对双足机器人混合动力学系统的辨识问题，以双足机器人运动过程中最为复杂的混沌步态作为辨识对象，提出一种基于混沌粒子群优化算法［17］优化的径向基函数神经网络（CPSO⁃RBFNN）和DFNN的双足机器人混合动力学系统辨识方法。

1 双足机器人混合动力学系统辨识可行性分析

本文立足于双足机器人摆动阶段与碰撞阶段之间存在的变量耦合、转换关系，从双足机器人轨道渐进稳定性角度推导该混合系统的整体可辨识条件。

考虑双足机器人系统摆动阶段的微分方程：

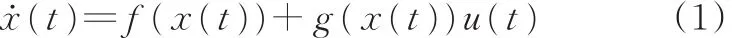
其中，x为系统的状态变量，x∈X；X是Rn中一连通的开子集；u(t)为系统控制输入，u(t)∈u⊂Rm；f为不确定参数的光滑非线性函数；g为系统非线性方程。假定：①系统中的所有状态均可测；②对于任意合理有界初始条件，系统在μ的作用下一致有界；③f、g为连续函数且满足局部Lip⁃schitz条件，则式（1）的解x(t)唯一。

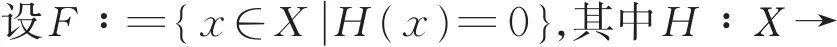
R。最后令Φ∶F→Χ。则对于存在碰撞作用的混合动力学模型，有

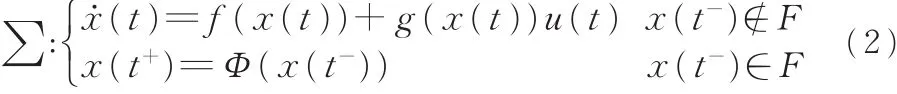
方程 φ:[t0,tf)→ Χ,tf∈R⋃{∞},tf＞t0为式（2）的解。如果：

（1）φ(t)在[t0,tf)上右连续；

（2）区间(t0,tf)上任一点的左极限存在；

（3）存在一个闭的离散子集Γ⊂[t0,∞)；则满足：

（1）对于任意t∉ Γ,φ(t)均可微且dφ(t)dt=f(φ (t))+g(φ (t))u(t)；

（2）如果t∈Γ，φ(t-)∈ F且φ(t+)= Φ(φ(t-))，则碰撞时间集为闭集，且仅有一个碰撞点。

若u(t)=0，则式（2）为时不变系统。对任意ε＞0，若O存在一个开邻域P使得任意p∈P，则式（2）存在一个解φ:[0,∞)→Χ满足φ(0)=p，并且对于所有t≥0，若满足二者间距离δ(φ(t),O)＜ε，则周期轨道O为李雅普诺夫稳定。如果O存在一个开邻域P，使得对于任意p∈P，式（2）存 在 一 个解 φ:[0,∞)→Χ 满足0，则轨道O是吸引的。如果轨道O既是稳定的，也是吸引的，则轨道O是李雅普诺夫渐进稳定的。

由式（2）可知，碰撞集合F={ |x∈Χ H(x)=0}，其中，H∶Χ→R为连续可微。如果式（1）的解与F交集的闭仅为一个点xˉ∶=Oˉ⋂F，且道Oˉ穿过F而不是与F相切，其中，Oˉ为轨道O的闭集。

对于存在碰撞作用的时不变双足机器人系统：

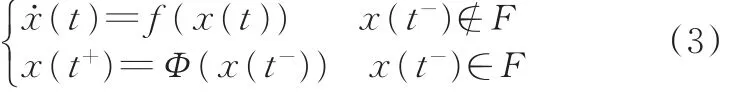
采用庞加莱截面法拓展上述非平凡的周期轨道，使其穿越F，并令φ为满足x˙=f(x)的解。

为实现这一拓展需作如下假设：①f(x)在Χ上连续；②对于给定的任意初始条件，式（4）的解唯一且连续依赖于初始条件；③存在一个可微的函数H∶Χ→R，使得F={ |x∈ Χ H(x)=0}，连续的，其中，F为源自于X的子集拓扑。

定义碰撞时间函数TI(x0)∶Χ→R⋃{∞}为

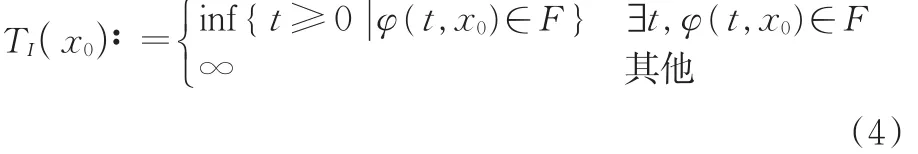
引理1 如果假设①～③成立，则TI在点x0连续，其中，0＜TI(x0)＜ ∞且LfH(φ (TI(x0),x0))≠ 0［18］。

在满足假设①～④的条件下，取定庞加莱截面为碰撞开始时刻对应的状态空间，则庞加莱回归映射P(x)∶=φ(TI(Φ(x)),Φ(x))是连续的。由于x0作为轨道迭代的初值，并且是相轨迹与庞加莱截面的交点，具有唯一性，即x0=Oˉ⋂ ～F，因此可以利用x0作为自变量去映射一整条周期轨道O(Φ (x0))。

引理2 满足假设①～③时，d∶～X→R在O上连续［18］。

定理1 如果假设①～④均满足，则下列命题成立：①如果O是式（3）穿越F的周期轨道，则存在点x0∈～F生成O；②当且仅当Φ(x0)生成的周期轨道穿越F时，x0∈～F为P的不动点；③当且仅当轨道O(Φ(x0))是李雅普诺夫稳定的，x0∈～F为xk+1=P(xk)的稳定平衡点；④当且仅当轨道O(Φ (x0))是李雅普诺夫渐进稳定的，x0∈ ～F为xk+1=P(xk)的渐进稳定平衡点［18］。

若O是穿越F的给定周期轨道，且x∈～X，TI(x)，满足 φ(t-,x)= φ(t,x)。

对于式（2）所表示的双足机器人系统，g(·):R2n+1→Rn是不确定非线性连续函数。由于g(·)与控制输入u为连续函数，故上述理论推导同样适用于式（2）。将第n次足地间碰撞时刻记为tn，碰前碰后时刻分别由tn、t+n表示。对于t∈[0,∞)时刻机器人的步态x(t)，显然存在自然数n，使得tn≤t＜tn+1。设ϑ为第n次碰撞后到当前状态的相对时间。令t=ϑ+tn,ϑ≥0，则步态x(t)可以表示为

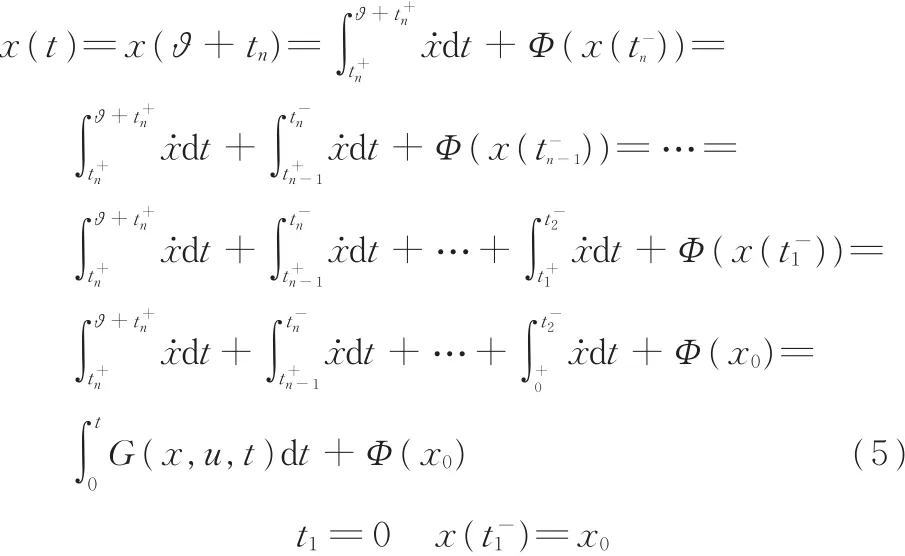
2 基于CPSO的RBFNN

本文利用CPSO⁃RBFNN强大的逼近能力与快速学习能力对双足步行中的摆动阶段建模，从而达到对该阶段动力学模型的准确辨识。RBFNN一般由输入层、隐含层和输出层组成［19］。假设网络输入Xn=［xn1xn2… xnm］，实际输出Yn=［yk1yk2… yks］，那么该网络的输入输出映射关系可表述为

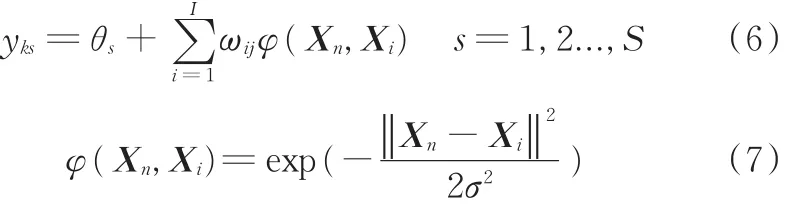
式中，n为训练样本数；S为输出单元个数；I为隐含层节点数；Xi为基函数的中心，Xi=［xi1xi2… xim］∈R1×m；θj为网络阈值；ωij为网络连接权值；σ为基宽。

式（9）中的基函数φ为高斯函数，RBFNN的精度主要由中心节点、基宽、阈值等参数决定。

CPSO算法是在粒子群优化（particle swarm optimization，PSO）算法［20］的基础上发展而来的一种新型群智能仿生优化算法，它在每次迭代寻优的过程中由混沌序列随机产生若干粒子并映射至原有解空间，从中选取适应度较高的个体替换原有粒子，作为下次迭代的初始种群。该算法能大大增加粒子种群多样性，避免陷入局部最优值，提升算法在解空间的寻优能力与收敛速度［21］。因此，本文采用CPSO算法对RBFNN的Xi、σ和ωij同时优化，从而得到最优的摆动阶段动力学辨识模型。

CPSO⁃RBFNN训练主要包括以下几个步骤：

（1）粒子群参数初始化，主要包括种群规模、最大迭代次数、惯性权重、学习因子、位置和速度取值区间等。

（2）建立RBFNN并生成粒子群，利用混沌序列初始化粒子种群与速度。

（3）计算粒子适应度函数值，对于本文，第i个粒子适应度计算公式为

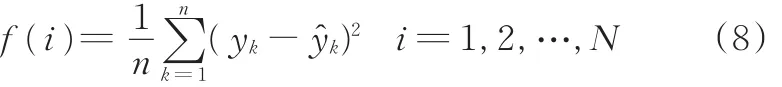
式中，yk为神经网络实际输出值；y^k为期望输出值；N为种群个数。

计算种群内各个粒子适应度，并把当前种群中适应度最低的粒子位置设置为全局最优位置。

（4）按照标准粒子群算法更新粒子的位置与速度［20］。对于适应度函数值小于种群平均适应度值的粒子，利用Logistic映射进行混沌优化。具体优化过程见文献［22］。

（5）当迭代次数小于最大迭代次数时，返回步骤（3），否则结束粒子群寻优。将最优粒子解码后，赋值给RBF中心、基宽向量和网络权值，得到最优的辨识网络。

3 动态模糊神经网络DFNN

在双足步行中，理想化的碰撞阶段可视为单次迭代过程［23］。鉴于机器人混沌步态对初值的敏感性，需寻找一类泛化能力强的神经网络识别未训练样本，以弥补辨识结果的误差，防止后续迭代中的误差累计使辨识结果迅速偏离原有混沌轨道。为此，本文采用DFNN来辨识该碰撞阶段。该网络由输入层、模糊化层、规则层、结论层和清晰化层组成。网络拓扑结构如图1所示，其本质是代表一个基于TS模型的模糊系统，其中，x1、x2、…、xr为网络输入，y是系统的输出，Mij是第i个输入变量的第j个隶属函数，Rj表示第j条模糊规则，Nj是第j个归一化节点，wj是第j个规则的结果参数或者连接权，u为系统总规则数。对该网络更详细的描述见文献［14］。

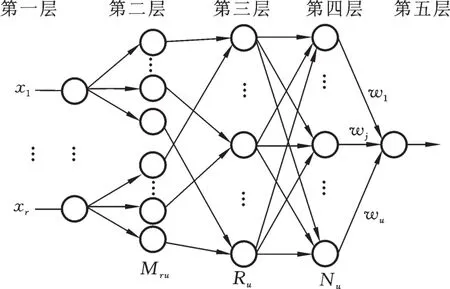
图1 动态模糊神经网络结构Fig.1 Structure of dynamic fuzzy neural network

DFNN训练过程主要包括以下几个步骤：①选取训练样本中的第一组数据作为系统观测数据，建立系统的模糊规则，得到对应的规则强度。②对高斯隶属度函数的中心和宽度进行修正，使系统性能指标达到期望值。③依次把训练样本中的数据送入DFNN，并重复步骤①、②。利用每次迭代学习的过程，增加有用或者剔除无效模糊规则，不断修正现有的规则库，使神经网络满足辨识精度要求。当达到最大迭代次数之后，网络训练结束。④利用修正的网络模型去预测碰撞结果，进而实现双足机器人碰撞阶段的准确辨识。整个辨识原理如图2所示。

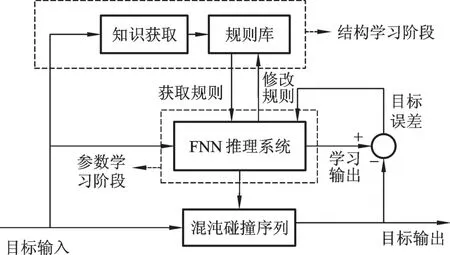
图2 碰撞阶段辨识原理图Fig.2 Schematic diagram of identification in collision stage

4 联合辨识算法设计

分别利用CPSO-RBFNN和DFNN对双足机器人碰撞阶段、摆动阶段准确辨识后，利用两阶段之间存在的变量耦合、转换关系，实现对机器人动力学系统的整体辨识与步态预测。联合辨识算法如下：

（1）设定双足机器人初始状态变量；

（2）设定预测步数S0，并令初始步数S=0；

（3）将初始状态点送入CPSO-RBFNN，辨识摆动阶段动力学方程系数矩阵；

（4）利用四阶Runge-Kutta思想完成辨识方程求解，求解终止条件为θ1= θ2-2β3；

（5）记录摆动终止时机器人各状态变量，送入DFNN得到碰撞后各状态值；

（6）左右腿角色互换，即θ+1=θ+2和θ+2=θ+1，其中，θ1、θ2分别表示支撑腿与摆动腿角度，上角标“-”和“+”分别表示碰撞瞬间的前后时刻，下同；

（7）判断是否满足辨识步数要求，即是否S=S0，若满足，则算法停止；否则令S←S+1，返回步骤（3）。

5 仿真结果与讨论

双足机器人行走步态主要包括极限环步态、倍周期分岔和混沌步态［24］，其中，混沌步态作为双足步行中最为复杂的步态表现形式，最能体现双足机器人动力学系统的复杂本质。若能解决双足机器人混沌步态的辨识问题，自然能把该方法推广至其他类型的步态辨识中。因此，本文以两连杆被动双足步行机器人所产生的混沌步态为辨识对象来验证DFNN与CPSO⁃RBFNN的联合辨识效果。

5.1 双足机器人混合动力学模型

本文的双足被动机器人模型如图3所示，该模型由2个完全相同的刚性直腿组成，两腿由髋关节点H相连。模型详细参数与取值见文献［18］。

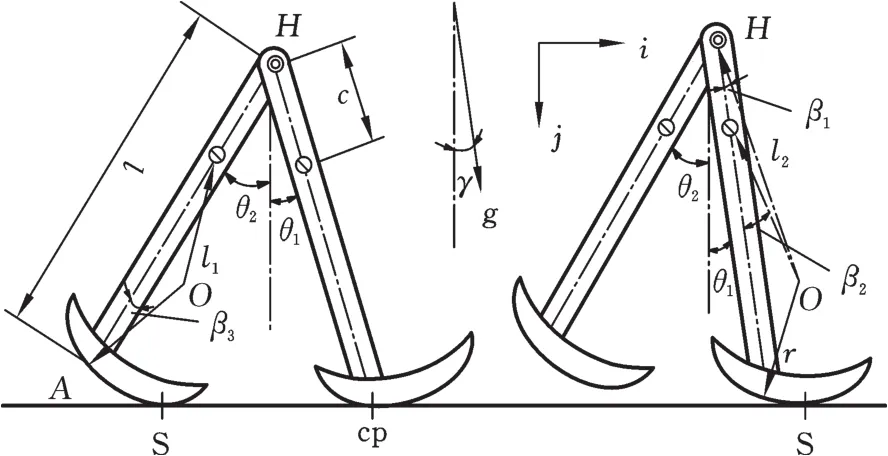
图3 机器人模型示意图Fig.3 Model structural diagram of biped robot

在对双足机器人运动过程做出若干理想化假设后［23］，分别利用拉格朗日法和角动量守恒关系推导运动中摆动阶段和碰撞阶段模型，得到该模型混合动力学方程：

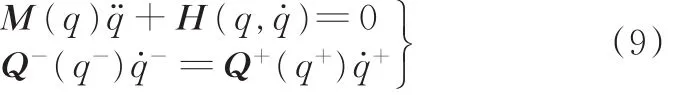
其中，M（q）为2× 2正定质量惯性矩阵；H(q,q˙)为重力、离心力和哥氏力之和；矩阵Q-、Q+由角动量守恒关系得到。

碰撞后两腿的角色互换，故有

式（9）、式（10）构成了完整的双足机器人混合动力学模型。

5.2 基于CPSO”RBFNN的摆动阶段辨识

为准确描述双腿运动过程，首先通过调整斜坡倾角γ使机器人呈现混沌步态。利用庞加莱映射的方法，分析机器人步态随γ变化的情况。取足地碰撞后的瞬间为庞加莱截面，图4为斜坡倾角γ ∈[0.13,0.172]（rad）时，庞加莱截面上 θ1的分岔图。由图4可知，随着γ的逐渐增加，机器人步态逐渐从单周期过渡到倍周期分岔直至混沌。把图4中矩形窗口区域进一步放大，可得图5。由图 5可知，当γ∈[0.164729,0.172]（rad）时，机器人步态表现为完全混沌。在此，本文利用γ=0.171rad时机器人混沌步态所产生的状态点列作为CPSO-RBFNN的辨识样本集。

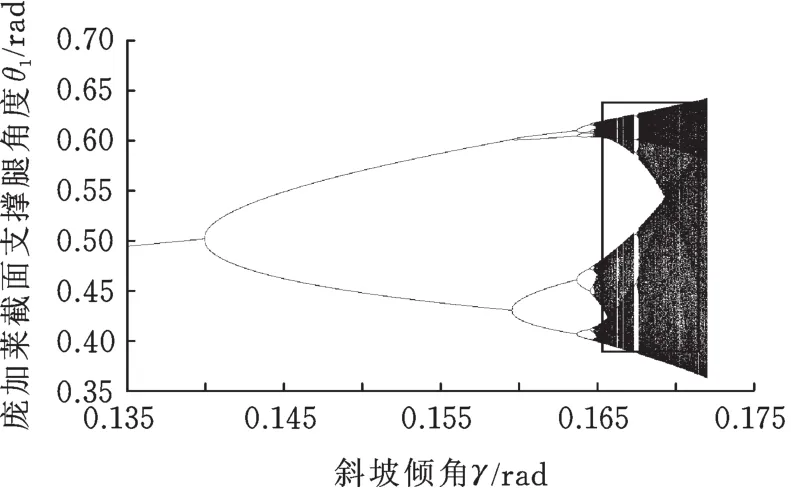
图4 庞加莱截面θ1分岔图Fig.4 The final state diagram ofθ1on the Poincaré section

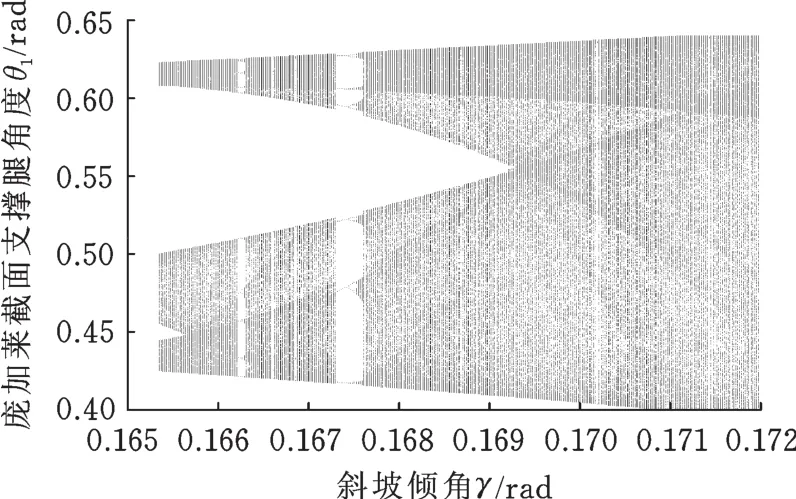
图5 混沌终态区域Fig.5 Chaotic terminal region

为得到较为丰富的摆动阶段神经网络学习样本集，从任意合适的初值状态点开始迭代2万次，以充分遍历混沌区域。随机选取其中5 000组数据点集，并依次代入式（9），得到5 000组摆动方程各项系数点列{M11，M12，M21，M22，H1，H2}，把前 4 500组数据作为训练样本集，后500组数据作为测试样本集。考虑到摆动阶段动力学方程中M12=M21且M22为定值，因此确定神经网络输入输出参数集分别为[θ1,θ˙1,θ2,θ˙2]和{M11，M12，H1，H2}。

训练中，CPSO⁃RBFNN各项参数取值如下：种群规模n=50，惯性权重w=0.7，学习因子c1=c2=2，最大迭代次数imax=80，神经网络隐层节点数设为60。图6所示为适应度函数的收敛过程。神经网络训练完成后，利用测试样本检验网络辨识与预测性能，其中，M11预测误差曲线见图 7。取定 [θ1,θ˙1,θ2,θ˙2]=［0.607 6，-1.794 7，-0.607 6，6.081 2］（rad），利用四阶Runge-Kutta法完成对辨识所得动力学方程的求解。图8所示分别为机器人角度与角速度的辨识结果，可见摆动阶段辨识结果具有较高准确度。

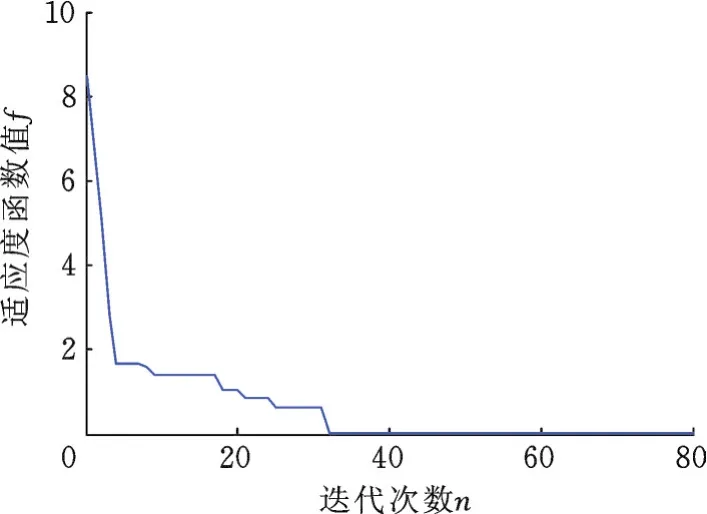
图6 适应度曲线Fig.6 Fitness curve

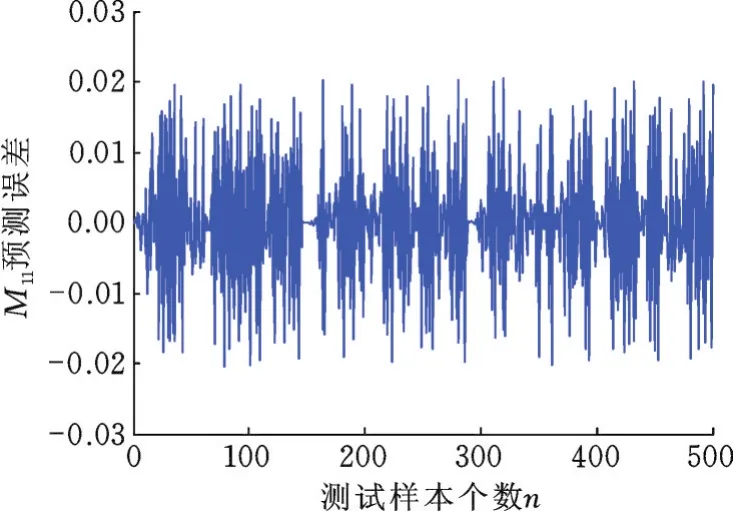
图7 M11项预测误差Fig.7 Prediction error ofM11

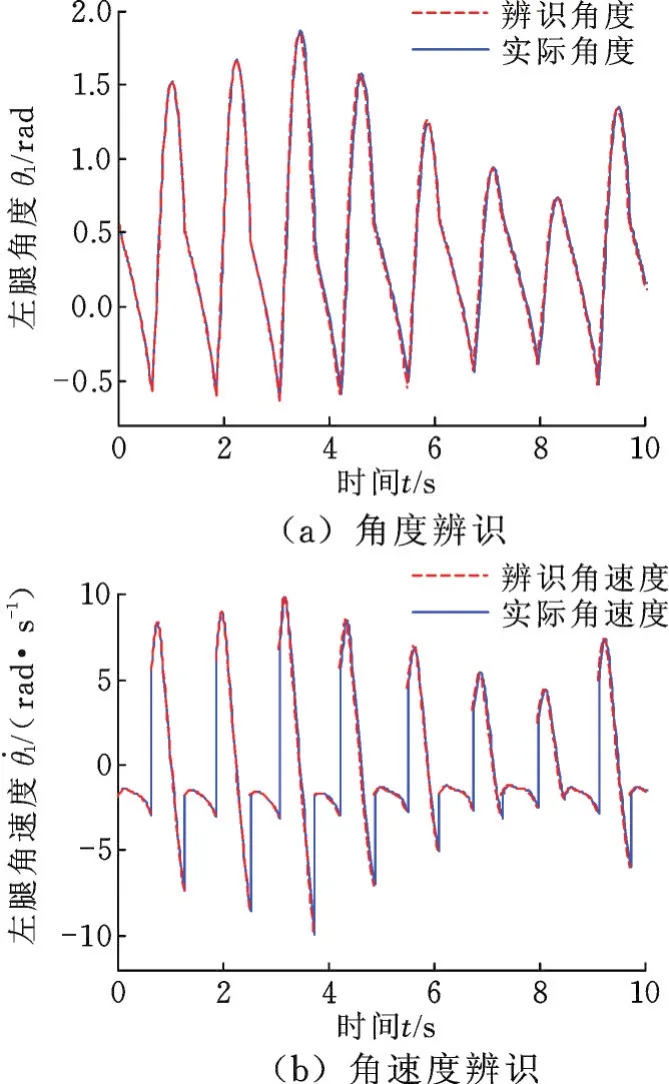
图8 摆动阶段辨识Fig.8 Identification in swing stage

5.3 基于DFNN的碰撞阶段辨识

双足机器人碰撞阶段模型描述为x(t+)=Φ(x(t-))，因此碰撞阶段可视为单次的迭代。为获得碰撞阶段的辨识样本，从斜坡倾角γ∈[0.165,0.172]（rad）的范围中均匀选取 20个值。对于每个斜坡倾角，记录300个步态周期碰撞后1 000组作为测试集。由于碰撞前后仅角速度产生突变而角度保持不变，因此选取输入参数集为[θ-1,θ˙-1,θ˙-2]，输出参数集为[θ˙+1,θ˙+2]。

鉴于双足机器人碰撞阶段对网络辨识精度具有较高要求，故把学习系统的输入输出变量的定义域精细划分为9个区间。以θ-1为例，图9表示θ-1的初始隶属函数曲线与学习后的修正隶属函数曲线。图10所示为学习后输入输出变量的映射关系。训练后的神经网络输入输出变量的隶属函数模糊标记为9个，分别用阿拉伯数字2～8表示，其中，1表示最小，9表示很大，最终得到的模糊规则如表1所示。

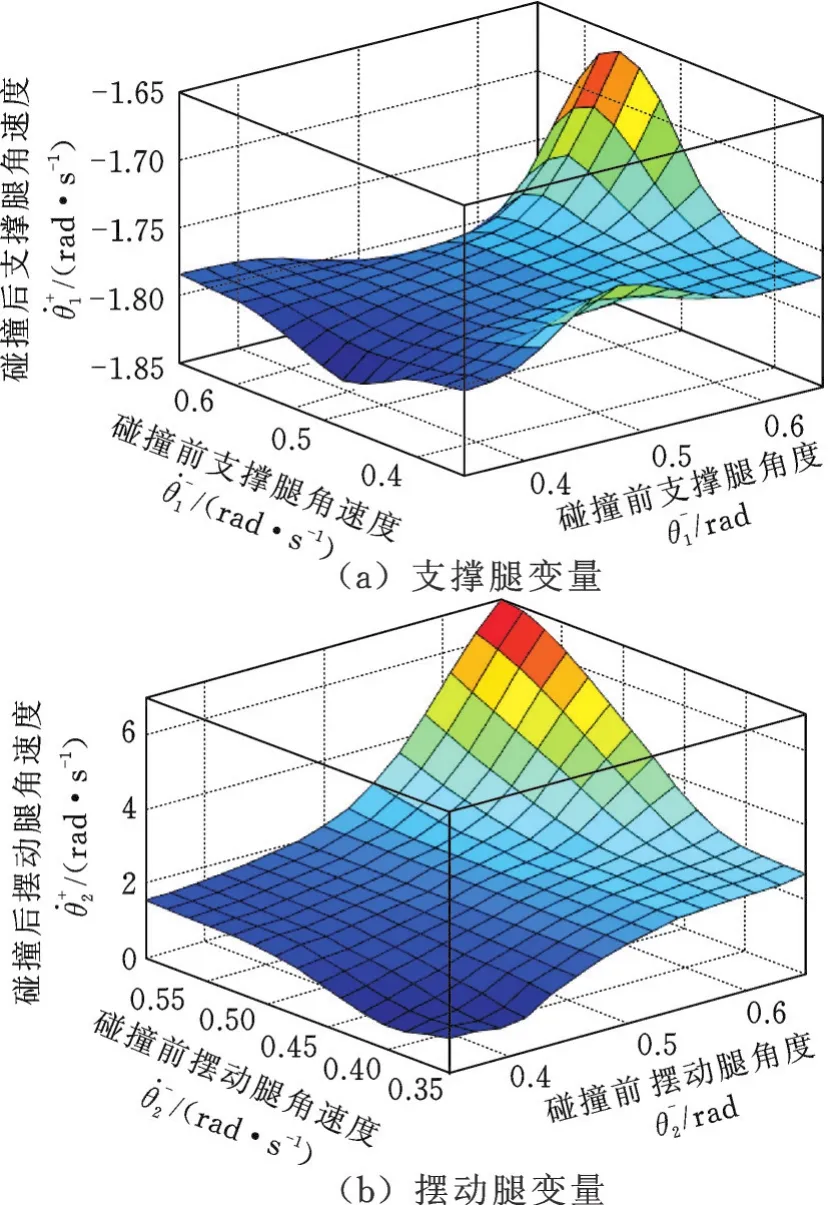
图10 输入-输出变量学习后的映射关系Fig.10 Mapping relationship of input”output variables after learning

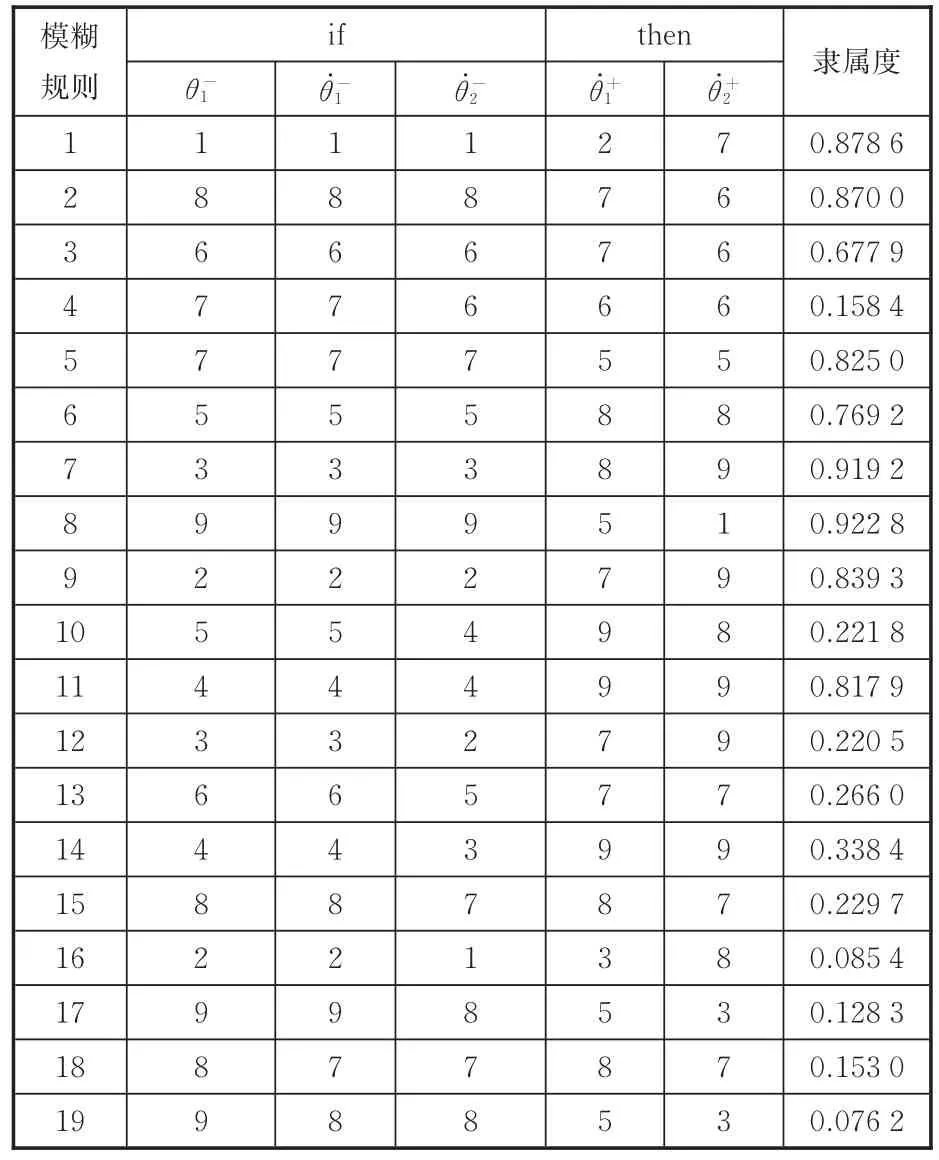
表1 自适应学习后模糊规则与其隶属函数Tab.1 Fuzzy rules and its membership function after self-adaptive learning

5.4 联合辨识

在分别获得了机器人行走步态碰撞阶段、摆动阶段的高精度辨识后，将两个阶段进行结合，采用第4节的联合辨识算法，实现对机器人混沌步态的完整辨识。

为验证联合辨识算法的有效性与精确度，同样选取斜坡倾角γp=0.171rad下的混沌步态作为辨识目标。由图11可知，在双足机器人初始行走的10步内，辨识步态几乎完全匹配混沌步态。10步之后的混沌步态辨识中，由于每次迭代过程中的误差累计，辨识精度会逐减降低，但辨识轨迹仍然紧紧跟随混沌轨道，直至20步左右，仍然具有较高准确度，体现出该辨识方法的有效性。

6 结论

双足机器人是一个高度非线性的混合动力学系统，对双足机器人系统的准确辨识显得尤为困难。本文提出一种基于CPSO-RBFNN与DFNN的联合辨识方法，针对双足机器人行走过程中连续摆动阶段与离散碰撞阶段所具有的不同特点，充分发挥神经网络对复杂非线性系统的逼近能力来拟合双足机器人系统。仿真结果表明，该方法能够充分表征双足机器人系统的动力学特性，准确辨识和预测出双足步行运动中的混沌步态，从而为基于步态预测的控制方法提供一条新的思路。

图11 混沌步态辨识曲线Fig.11 Identification of chaotic gait