考虑公差的扭转动力吸振器不确定性优化设计
2018-09-22郝耀东何智成李光耀张卓敏
郝耀东 何智成 李光耀 张卓敏
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082 2.中汽研(天津)汽车工程研究院有限公司,天津,300399
0 引言
当前,汽油、柴油发动机仍然是汽车动力系统的主要形式。就汽油机和柴油机而言,其输出的扭矩是周期性波动的。这种周期性变化的激励作用于动力传动系统,引起各部件转速的不均匀,是造成动力传动系统扭转振动的根本原因[1]。发动机输出激励的波动无法避免,但当激励扭矩的作用频率与动力传动系统固有频率相近,引发共振时,就会造成动力传动系统的剧烈振动。这种剧烈的扭转振动通过传动轴支撑、后桥、后悬等结构传递至车身,并与声腔相耦合,就会引发车内轰鸣。这种轰鸣通常是手动变速箱前置后驱车型最严重的NVH(noise,vibration,harshness)问题之一[2]。
关于动力传动系统扭振轰鸣的机理和解决方法,国内外学者进行了很多研究。CODERC等[3]设计了一套动力传动系统振动试验台架以测量发动机激励下系统的扭振性能;侯东晓等[4]采用拉格朗日方程建立了旋转机械传动系统的连续动力学模型,并通过传递函数法推导出任意轴上的扭振响应公式;王登峰等[5]通过三维实体建模、试验和计算获取动力传动系动力学参数,并分析了双质量飞轮扭振减振器对动力传动系固有特性及强迫振动响应特性的影响;张代胜等[6]利用偏导数法分析得出汽车动力传动系无阻尼自由扭振固有频率和振型对转动惯量和扭转刚度的灵敏度。
在实际工程应用中,动力传动系统参数常常无法进行设计修改。如改款车型和同平台车型为了保证零部件的共用性,动力传动系统往往直接借用;又如车辆开发后期,动力传动系统参数的更改会导致车身结构的相应更改和动力总成的重新调校,耗费大量人力物力;再如由于总布置、动力性、经济性等其他性能的限制,动力传动系统参数只能进行微调,致使其振动性能变化不大。在这种情况下,在动力传动系统中加入扭转动力吸振器(torsional vibration damper,TVD)可以快速有效地解决动力传动系统的NVH问题。目前关于扭转动力吸振器的研究主要集中在应用方法和效果上,如赵艳影等[7]采用稳定性切换方法分析了时滞动力吸振器及其扭转振动系统的稳定性问题,分别得到了时滞动力吸振器和扭转振动系统的时滞稳定和不稳定区域;段龙扬等[8]结合某运动型多功能车的车内某转速下轰鸣声的控制问题,详细分析了问题的来源,采用加装TVD的方法控制该转速下的车内轰鸣噪声。
TVD需要在现有动力传动系统的基础上进行设计,其参数的选择取决于原模型的振动特性和TVD参数之间的匹配。传统的TVD设计只考虑了设计状态的动力传动系统模型,但实际上,动力传动系统模型的参数是不确定的,这些参数会因设计、制造、使用状态的不同而发生变化。动力传动系统自身参数的设计需要考虑到这种不确定变化,TVD的设计也需要考虑到这种不确定变化,以便在不同制造条件和使用工况下均最大限度地满足减振及其他性能的要求。目前,基于不确定性的优化方法已经应用到汽车开发的很多领域,如动力悬置系统设计[9]、发动机扭矩管理[10]、车辆平顺性设计[11]等,但目前还没有研究将不确定性理论引入TVD设计中。
本文以某前置后驱MPV车型动力传动系统为例,基于区间不确定性模型和考虑公差的区间不确定性优化方法,对TVD的设计进行了研究。建立了带TVD的动力传动系统(TVD动力传动系统)模型,并推导了模型的动力方程;对TVD对动力传动系统振动的影响进行了分析和总结;将区间不确定模型引入TVD动力传动系统模型中,并基于考虑公差的区间优化模型对TVD参数进行了优化。
1 TVD动力传动系统振动模型的建立
在传统的前置后驱动力传动系统模型中,主减速器输入轴及差速器均相对地面旋转,后桥的作用被忽略了,而实际上,后桥对动力传动系统的振动有着不可忽略的影响,它不仅是动力传动系统振动传递至车身的主要传递路径之一,也会改变动力传动系统自身的模态和强迫振动响应。为了考虑后桥对动力传动系统的影响,郝耀东等[12]提出了动力传动系统-后桥耦合模型(driveline and rear axle coupled torsional vibration model,DRCTVM)。在DRCTVM中,主减速器输入轴及差速器均安装在后桥壳上,同时,后桥壳通过扭转弹簧和扭转阻尼与大地相连。这样,后桥与动力传动系统的关系得以考虑进来,试验结果表明,DRCTVM具有更高的精度。
在DRCTVM中加入TVD元件,动力传动系统几何机构见图1,建立的TVD动力传动系统模型见图2。图2中加粗部分即表示TVD元件。动力传动系统主要零部件的简化方法如下:①将发动机运动机构简化为一个转动惯量,发动机输入扭矩T就加载在这个转动惯量之上;②将离合器简化为一个弹簧阻尼系统,其扭转刚度和扭转阻尼均取离合器主减振阶段的值;③将变速箱简化为一个位于其输入轴位置的单自由度弹簧阻尼系统;④将传动轴和半轴均简化为位于轴末端的单自由度弹簧阻尼系统;⑤将TVD元件简化为一个单自由度弹簧阻尼系统。

图1 动力传动系统几何模型Fig.1 Geography model of driveline

图2 TVD动力传动系统简化模型Fig.2 Simplified model of driveline with TVD
图2 中,各符号的含义见表1~表2。其中,R1和R2分别表示变速箱和主减速器的传动比。

表1 简化模型中的转动惯量参数Tab.1 Inertia parameters in the driveline simplified model
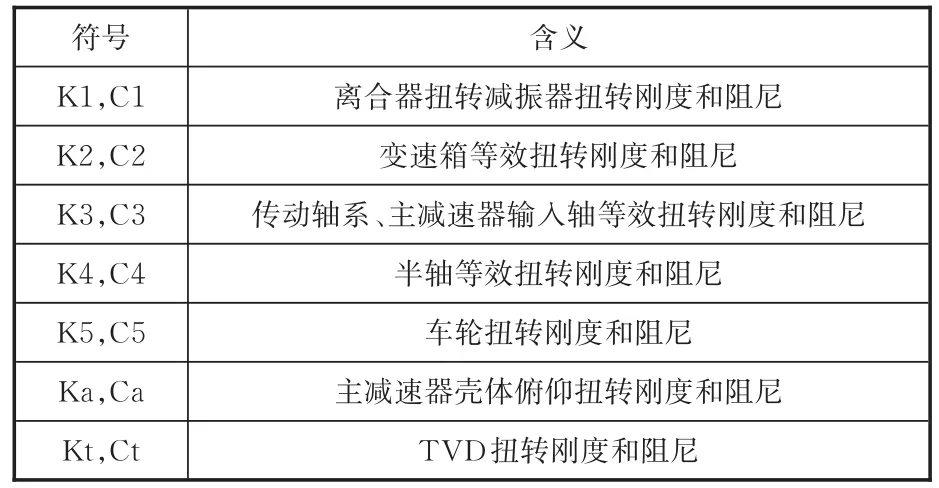
表2 简化模型中的扭转刚度和阻尼惯量参数Tab.2 Stiffness and damping parameters in the driveline simplified model
各零部件的转动惯量在数字模型中测量得到,扭转刚度则通过有限元方法计算获取。本文以变速箱3挡为例进行研究,当变速箱挡位为3挡时,动力传动系统简化物理模型中的各参数值见表3。

表3 动力传动系统简化模型参数Tab.3 Values of parameters in the driveline simplified model
由于传动比的存在,动力传动系统各元件转速不同,在等效过程中,需要对各元件的转动惯量和扭转刚度进行转化,将从动轴的转动惯量和扭转刚度转化到主动轴上。令r表示传动比,ϕ1、ϕ2分别为主动轴和从动轴的转角,其中,ϕ1=rϕ2,k、c、m分别表示转化前系统的扭转刚度、扭转阻尼、转动惯量信息,k′、c′、m′分别表示转化后系统的刚度、阻尼、转动惯量信息。转化前后系统的能量不变,可得
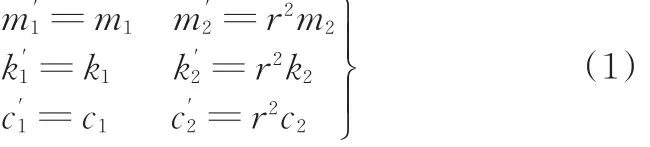
根据式(1)即可将各元件的转动惯量、扭转刚度和阻尼均等效至输入元件处。
根据式(1)对模型中的惯量、刚度、阻尼参数进行转化,消除模型中的传动比,则动力传动系统物理模型可以转化为图3所示的模型。
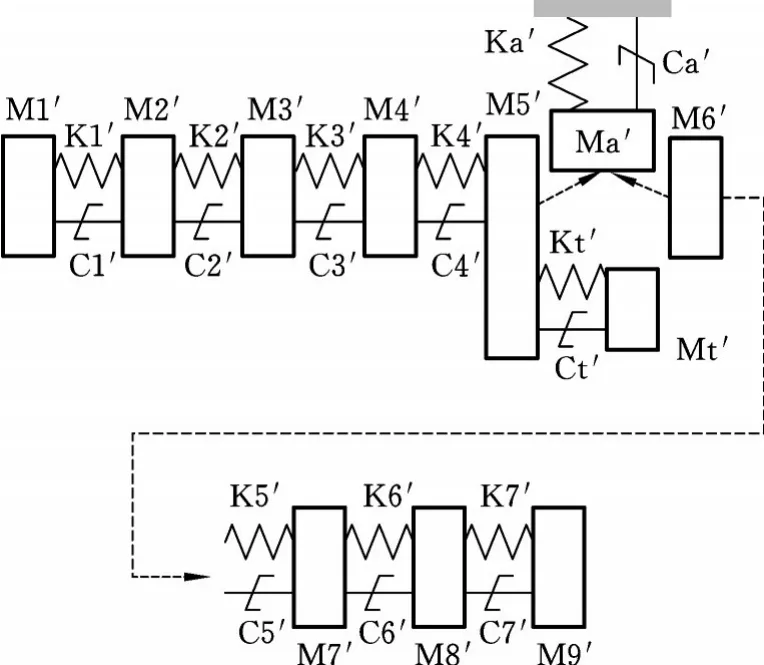
图3 传动比转化后的动力传动系统物理模型Fig.3 Driveline model after transform
通过拉格朗日方程来建立动力传动系统扭振动力方程,令θ′表示模型中各转动惯量的转角,可得动力传动系统扭振动力方程:

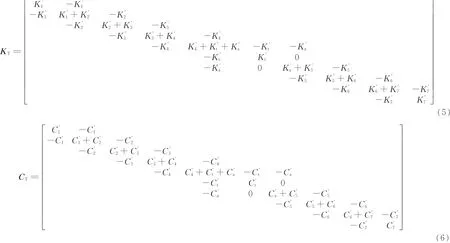
2 TVD动力传动系统振动性能分析
对TVD动力传动系统进行自由振动分析,并与未安装TVD的动力传动系统进行对比,系统模态频率见表4,关键模态振型见图4。

表4 TVD动力传动系统固有频率Tab.4 Nature frequencies of driveline system with TVD
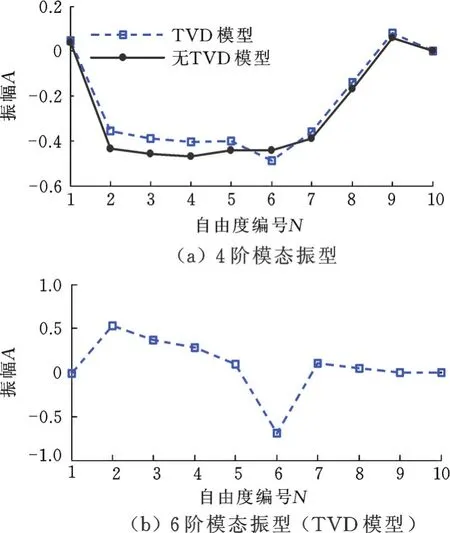
图4 TVD动力传动系统关键模态振型Fig.4 Modal shapes of drivline system with TVD
由表4和图4可知:添加TVD元件后,系统前3阶低频模态频率基本上没有变化;第4阶离合器模态频率有所下降,振型变化不大;第5阶后桥俯仰模态频率和振型均变化不大;加入TVD后,系统增加了第6阶模态,模态振型峰值位于TVD处,频率为76.4 Hz,高于TVD自身模态频率71.5 Hz;7阶以后的高阶模态由于模型计算频率范围的限制,其频率值精度较低,故不讨论。
将发动机二阶输出扭矩加载到TVD动力传动系统模型,发动机飞轮、变速箱输入轴与主减速器输入轴处的扭转加速度曲线,见图5。
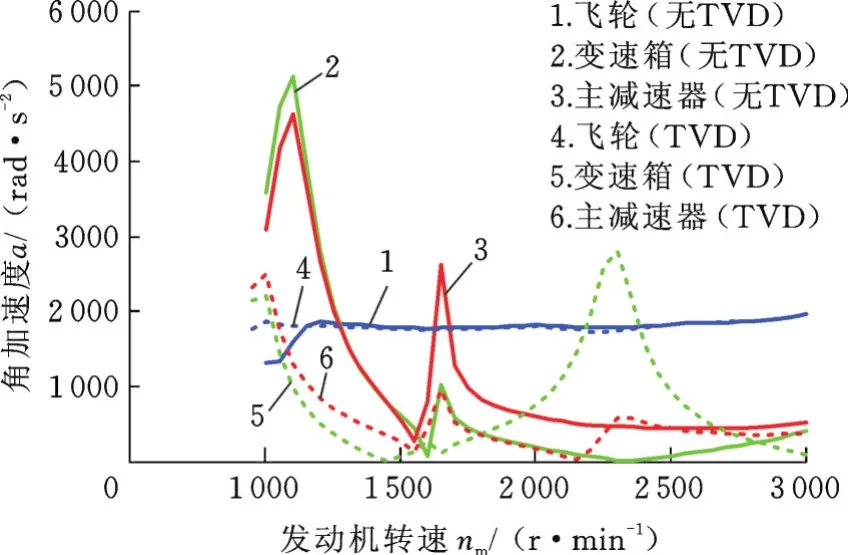
图5 TVD动力传动系统角加速度响应Fig.5 Acceleration responses of driveline system with TVD
由图5可知,加入TVD后,飞轮扭振加速度基本没有变化;变速箱扭振加速度第一峰值提前到900 r/min左右,即为30.4 Hz模态频率对应的转速,且幅值大大衰减;加速度第二峰值所处位置不变,但幅值也明显衰减,和模态频率的变化相对应;而在2 300 r/min左右,也就是TVD动力传动系统增加的模态频率76.4 Hz对应的转速下,变速箱扭振角加速度均增加了一个峰值,且其值非常明显。对于主减速器输入轴,其扭振加速度第一峰值同样提前到30.4 Hz对应的转速且幅值明显衰减;加速度第二峰值也具有位置不变和幅值衰减的特征;而在2 100 r/min左右,即TVD自身模态频率所对应的转速范围内,振动衰减最为明显,曲线有明显的谷值;在2 300 r/min左右,主减速器扭振角加速度同样出现峰值,但该峰值不明显。
综合TVD动力传动系统自由振动和强迫振动分析结果,可得以下结论:①加入TVD元件后,动力传动系统新增一阶模态,模态振幅峰值位置位于TVD处,其他阶模态频率也会发生变化,但振型基本不变;②响应曲线共包括3个峰值,相对于原动力传动系统增加了1个峰值,峰值位置均位于系统模态频率处;③加入TVD元件后,动力传动系统扭振加速度水平在大部分频率范围内明显降低,在TVD自身模态频率处衰减最为明显;④在TVD动力传动系统新增模态频率处,会出现新的扭振加速度峰值,该峰值在远离TVD安装位置处更为明显。
3 TVD动力传动系统振动的区间不确定性分析
3.1 TVD动力传动系统的不确定性描述
TVD动力传动系统参数众多,需选择灵敏度较大的参数作为不确定变量。设x和g(x)分别表示动力传动系统参数和扭振性能,定义g(x)对x的灵敏度为
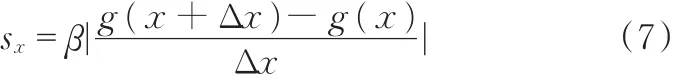
其中,Δx为x的微小增量,β表示比例因子,对于不同的性能和系统参数,β可以取不同的值。以系统模态频率及响应曲线峰值作为评价系统扭振性能的标准,根据式(7)计算系统各参数的灵敏度,部分计算结果见表5。

表5 TVD动力传动系统参数灵敏度Tab.5 Sensitivities of parameter
由灵敏度计算结果可以看出,转动惯量参数M2、M5、M6、M7、Ma、Mt和扭转刚度参数 K1、Ka、Kt对TVD动力传动系统振动有明显的影响,故选择这9个参数作为不确定变量。
对于TVD动力传动系统参数,在车辆开发过程中大量测量样车参数数值是不可能实现的,因此,本文采用区间模型描述不确定变量的不确定性,以变量的设计值为区间模型中心值,区间半径则参考制造公差和以往经验值进行选取。各不确定变量的中心值和区间半径数值见表6。
3.2 TVD动力传动系统的区间摄动模拟
鉴于蒙特卡罗方法计算量巨大,本文采用区间摄动法[13]计算TVD动力传动系统的振动不确定性。设b表示区间不确定变量向量,bC表示区间变量中间值向量,Δb表示区间变量区间半径向量,和分别表示区间变量上界向量和下界向量。则有

表6 区间变量不确定模型的相关参数值Tab.6 Values of parameters in the interval models

设F(b)表示TVD动力传动系统振动响应向量,则有

式中,f4、f5、f6分别为系统第4、5、6阶模态频率;Ag1、Ag2、Ag3分别为变速箱输入轴扭转加速度的3个峰值;Am1、Am2、Am3分别为主减速器输入轴扭转加速度的3个峰值。
将F(b)展开成泰勒级数的形式,由于级数阶次的增加,将大大增加计算规模,而提高的精度则十分有限,故本文采用一阶泰勒级数对F(b)进行展开:

其中,FC、ΔF分别表示系统振动响应向量的中心值变量的灵敏度,其结果已求出(表6、表7),响应向量的上下界可根据中心值和区间半径进行计算:

将参数值代入式(10)和式(11)中,计算各振动响应指标的中心值、区间半径和上下界,计算结果见表7。
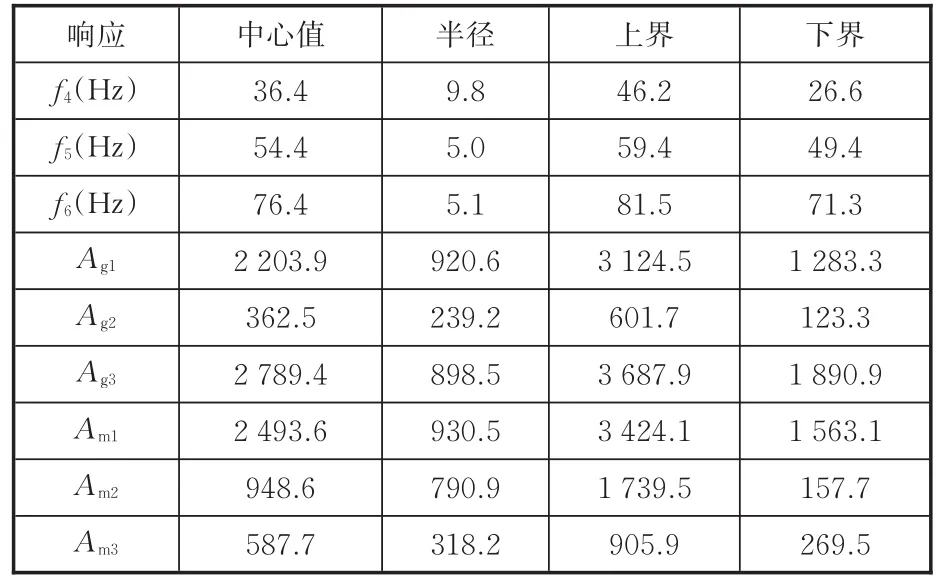
表7 系统振动响应的区间不确定性模拟结果Tab.7 Results of interval uncertainties of vibration responses
由表7可知,当不确定变量在区间内波动时,TVD动力传动系统模态频率会产生较大波动:系统第4阶模态摄动半径达到9.4 Hz,变化范围在26.6~46.2 Hz之间,第5、6阶模态频率的摄动范围也分别达到10.0 Hz和10.2 Hz。变速箱输入轴和主减速器输入轴处的振动加速度峰值也存在较大变化量,主减速器输入轴第二峰值的上下界甚至相差10倍,极容易在系统参数发生变化时,引起车内的扭振轰鸣、振动等问题。因此,优化TVD参数,保证系统振动响应在不确定条件下仍达到较高的标准,具有重要意义。
4 考虑公差的TVD区间不确定性优化
4.1 考虑公差的TVD区间优化模型的建立
在TVD制造过程中,往往先确定橡胶部分的结构,再通过改变橡胶材料配方逐步调节橡胶硬度,以逼近橡胶扭转刚度的设计值,在这个过程中,需要多次进行扭转刚度的测试才能达到理想的刚度结果。扭转刚度的设计公差值越小,测试和反复调配的次数就越多,极大延长了开发周期,增加了开发成本。TVD转动惯量也存在相同的问题,当转动惯量的设计公差越小时,惯量盘的加工要求就越高,加工时间和成本就会相应提高,零部件的合格率就会下降。因此,在设计阶段就对零部件参数的公差进行考虑,在可能的情况下增加设计公差,实现所谓的并行公差设计,可以有效解决设计公差带来的问题。
传统的区间优化模型[14]可以表示为
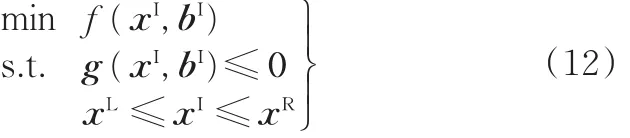
式中,xI为区间设计变量向量;f(xI,bI)为目标函数;g为约束条件向量;xR、xL分别为设计变量的上下界组成的向量。
由式(12)可以看出,尽管模型中引入了不确定变量,但优化结果仍是确定值,设计公差仍需根据制造与使用条件进行确定。本文将考虑公差的区间不确定优化方法引入TVD优化设计过程中,令设计变量向量

则设计变量的设计值向量和设计公差向量可以分别表示为
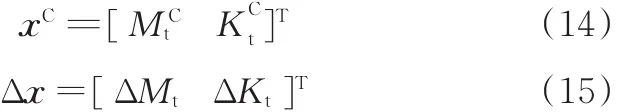
其中,MCt、KCt分别表示TVD转动惯量和扭转刚度的设计值;ΔMt、ΔKt分别表示TVD转动惯量公差和扭转刚度公差。设计变量的实际值则会在区间xI范围内波动。即

由式(16)可知,尺寸公差的表示方法与区间变量完全相同,区间半径Δx越大,变量的设计公差越大,制造时允许的精度等级就越低,成本也会相应降低;反之,Δx越小,制造时就必须采用较高的精度等级,制造成本、周期也会相应提高。因此,在TVD优化设计工程中,除保证动力传动系统的振动性能外,还需要保证向量Δx中各元素的值。本文采用公差评价系数η评估各设计变量公差水平的大小,即
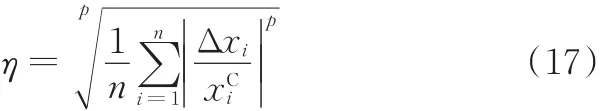
其中,n表示设计变量的个数,xCi、Δxi分别表示第i个设计变量的设计值和设计公差,p可取1或无穷大。当p取1时,η表示各设计变量的平均公差;当p取无穷大时,η表示各设计变量的最大公差。本文取p=1。由式(17)可以看出,η越大,系统允许的变量设计公差越大。
采用区间变量中心值确定的性能f(xC,pC)和公差评价系数η共同作为目标函数,则考虑公差的区间优化模型可以表示为
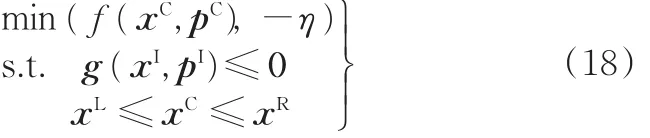
式(18)中,目标函数和设计变量取值范围都已经采用确定性方式进行描述,只需将约束条件g(xI,pI)≤0进行确定性转化,就可以采用经典的确定性优化方法进行优化求解。
设AI表示区间数,b表示一常数,根据概率理论,两者间的区间可能度关系可表示为[15]

采用式(19)对约束条件g(xI,pI)≤0进行转化,则考虑公差的区间优化模型可表示为

其中,gj表示模型的第j个边界条件;gRj、gLj分别表示边界条件的上下界;m表示约束条件的个数;λj表示第j各边界条件的可能度系数,其值越大,说明该约束越严格。式(20)可采用经典的确定性优化模型进行优化。
在TVD动力传动系统优化过程中,以TVD转动惯量和扭转刚度的中心值和区间半径为设计变量,设计变量见式(14)、式(15)。
以变速箱和主减速器输入轴扭转加速度峰值的几何平均值为目标函数,则目标函数可以写成

同时约束变速箱和主减速器扭转加速度曲线的各峰值均不超过优化前的值,各约束条件参数见表8。
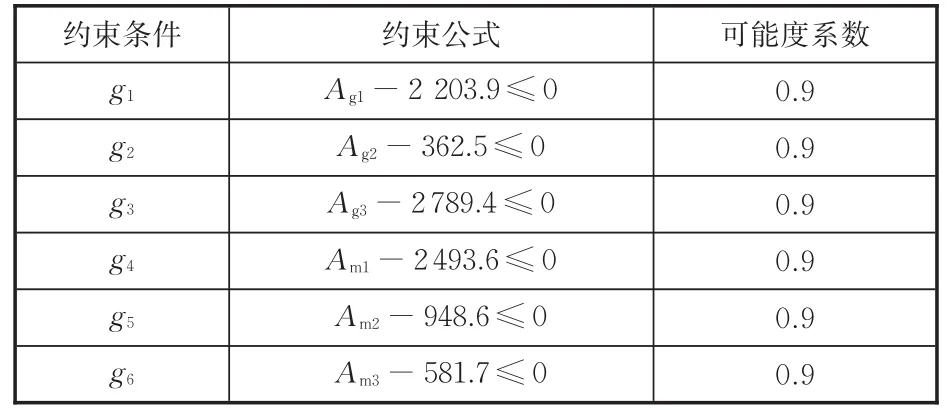
表8 优化模型约束条件Tab.8 Constraint conditions of optimization model
根据TVD的制造和安装条件,其转动惯量和扭转刚度变化范围可以表示为
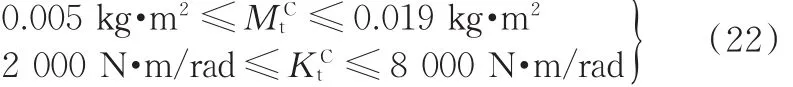
4.2 TVD参数优化结果及验证
采用NSGA-Ⅱ算法[16]求解TVD动力传动系统优化模型,其中,种群数目为48,遗传代数为80,优化结果见表9。
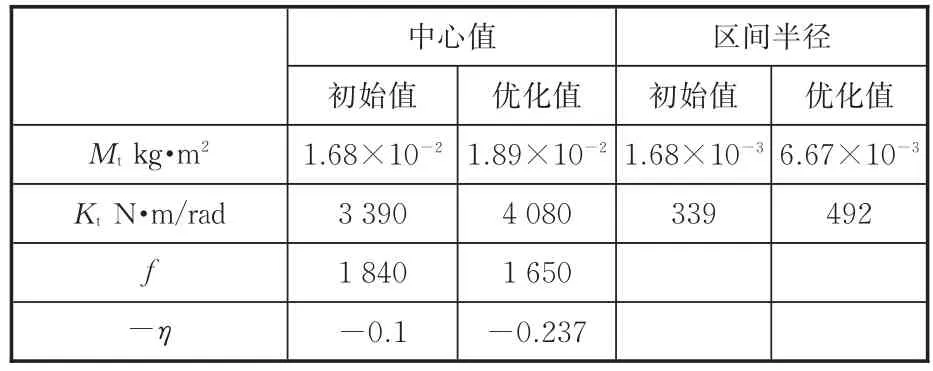
表9 TVD动力传动系统优化结果Tab.9 Optimization results of driveline system with TVD
由表9可知,优化后,f减小了10.3%,说明动力传动系统的振动峰值水平有所下降;同时η增大了137%,说明参数的设计公差大幅上升,其中,Mt的设计公差由1.68×10-3kg·m3上升至6.67×10-3kg·m3,Kt的设计公差由3.39×102N·m/rad上升至4.92×102N·m/rad。在设计公差大幅上升的同时,仍能保证振动水平的下降,充分证明本文方法的有效性。
将设计的TVD安装在MPV车型主减速器输入轴上,见图6,测量3挡全油门工况下车内驾驶员、中排乘客和后排乘客耳边噪声,测试结果见图7。

图6 扭转动力吸振器的安装Fig.6 Installation site of TVD
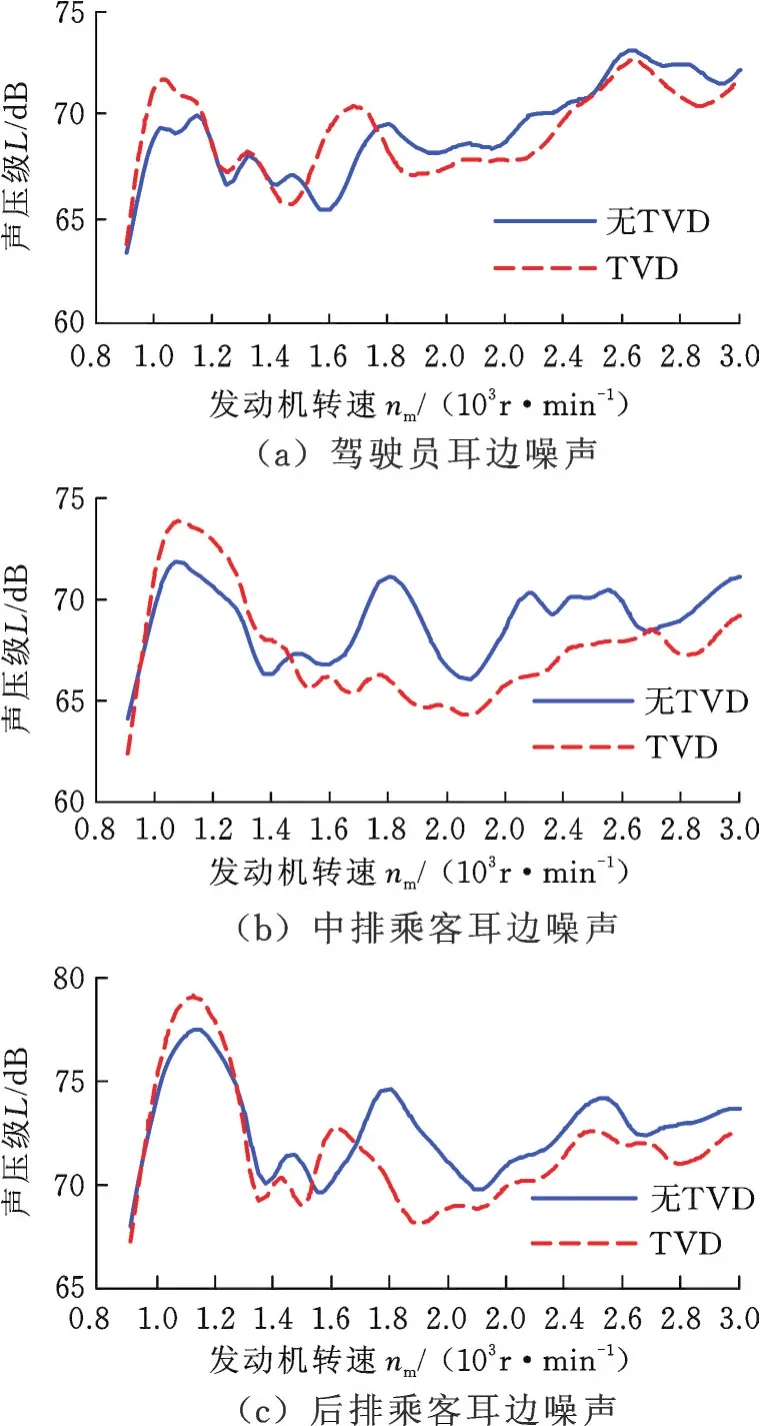
图7 三挡全油门工况下的车内噪声Fig.7 Interior noise in 3WOT conditoin
由图7可以看出,安装TVD后,车内噪声尤其是中、后排乘客耳边噪声在1 400 r/min以上的转速范围内均有明显下降,证明安装TVD可以有效解决动力传动系统振动引起的车内轰鸣问题。
5 结论
(1)加入扭转动力吸振器(TVD)元件后,动力传动系统扭振加速度水平在大部分频率范围内明显降低,在TVD自身模态频率处衰减最为明显,但在系统新增模态频率位置会产生新的振动峰值。
(1)建立了考虑公差的区间不确定性优化模型,以TVD参数为设计变量,TVD参数设计公差和动力传动系统振动水平为目标函数,该模型可以在显著提高参数设计公差的同时保证系统振动水平的下降。
(3)在某MPV车型上安装了扭转动力吸振器,测试结果表明,扭转动力吸振器可以有效降低由动力传动系统扭振引起的车内噪声。
