陷落柱突水的尖点突变模型研究

王 迁 李金华

（山西潞安集团司马煤业有限公司，山西 长治 047105）

煤矿水灾与瓦斯、粉尘、火灾和动力地质灾害并称矿井五大灾害，水害在煤矿重、特大事故中是仅次于瓦斯爆炸的重大灾害[1]。华北地区的陷落柱引发了多次大型突水事故，如徐州矿区张集煤矿、淮北矿区桃园煤矿和淮南矿区潘集二矿陷落柱突水事故，最大矿井涌水量均达到了10000m3/h以上。司马煤矿陷落柱较为发育（如图1所示），是矿井水害防治的重要隐患。

陷落柱突水通常具有渗流突变的特性，尤其是底板隐伏陷落柱形成与含水层的垂向导水通道，当煤层开采后，底板岩层的原始应力状态被破坏，致使应力重新分布，从而导致底板岩层失稳破坏形成导水裂隙，其结果往往造成底板承压水经由陷落柱通过采动裂隙突然涌入采煤工作面，形成陷落柱突水。煤层开采后，底板岩层失稳破坏形成的陷落柱突水现象，属于突变理论研究的范畴。因此，本文以突变理论为基础，建立底板隐伏陷落柱的滞后突水突变模型，为底板隐伏陷落柱的突水时机及状态判断提供强有力的理论支撑。

1 陷落柱突水的突变现象分析

以徐州矿区张集煤矿、淮北矿区桃园煤矿和淮南矿区潘集二矿为例对陷落柱突水现象进行说明[2-3]。陷落柱突水的流量演化过程如图2所示，在陷落柱突水过程中，工作面涌水量均出现了阶梯状的增长趋势。如徐州张集矿陷落柱突水过程如下：在1997年2月18日早班，于矿井西翼-300m水平太原组21号煤轨道下山往下掘进341.35m时，在掘进工作面退后约4m处发现该处两帮裂隙滴水；15时左右装岩机出矸后见到底板有一股直径约2m、高约0.2m的水流喷出，实测水量65m3/h；17时30分增至483m3/h，18时左右剧增到24098m3/h，19时30分，-300m泵房进水、淹泵、断电，最后全井被淹。淮北桃园矿和淮南潘集二矿的陷落柱突水实际监测过程中也均出现了与徐州张集煤矿类似的涌水量阶梯式增长的规律。

陷落柱突水过程中存在明显的渗流突变现象，而传统的理论计算方法渗流场都是连续变化的，如白海波等[4]提出的陷落柱塞子模型，武强等[5]提出的侧壁筒模型、王家臣等[6]提出的“渗水井”模型、杨天鸿等[7]提出的非线性渗流模型，上述模型无法解释陷落柱的渗流突变现象，因此应寻找一种可用于解释陷落柱突变现象的理论计算模型，这对揭示陷落柱的突水机理具有十分重要的意义。

图2 陷落柱突水的流量演化过程

2 陷落柱突水的尖点突变机理

原《煤矿防治水规定》[8]采用突水系数法对底板的突水危险性进行描述，其认为底板突水危险性与底板岩层厚度h和水压差ΔP有关。以尖点突变模型描述陷落柱突水现象时，选用MP为水压致突因子，其中ΔP为单位厚度底板岩层下的水压与煤层开采后工作面的水压（此位置处水压为0）之差，即水压差ΔP与底板岩层厚度h之比，M为正的系数；选用Nt1为时间因子，t1为水压对煤层底板岩层作用的有效时间，N为正的系数。MP和Nt1为控制陷落柱突水的两个基本因子，即两个控制变量。渗流速度μ1与突变时刻的渗流速度μ0之比Iμ为状态变量。控制变量、状态变量构成的尖点突变模型的平衡曲面和分支曲线如图3所示。对一定的采场而言，底板厚度h是不变的，煤层开采后由于应力的重分布导致水压差ΔP有所变化，增强了突水性能，当Iμ=μ/μ0＞1 时，便会引发突水。

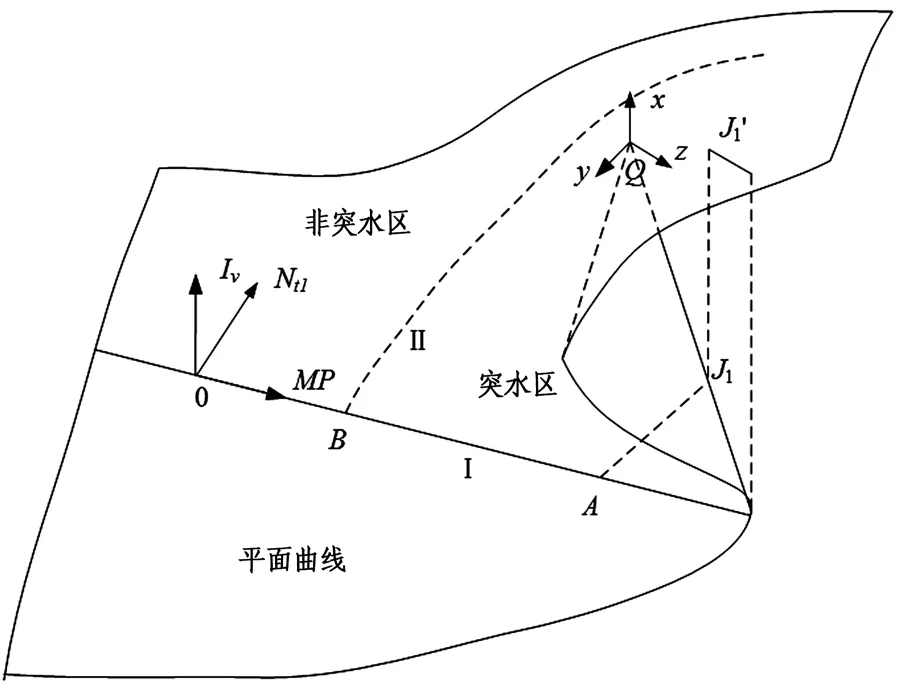
图3 平衡曲面与分支曲线

在图3中，当水压差ΔP较小时，曲线II由B点开始，随着Nt1的逐渐增加，Iμ渐变至突水区，无突变现象。当水压差ΔP很大，曲线I由A点开始，随着作用时间Nt1的增加而连续前进，其所对应的流速比Iμ亦随之逐渐增加，当达到J1点（对应点在控制平面上位于分支曲线上）时，若此时陷落柱内作用于煤层底板的水压的时间稍有增加，则底板岩层将失稳破裂，渗流速度比Iμ将会剧增，在图3中表现为系统状态由非突水区的J1点跳跃至J1′点达到突水区。

当水压作用时间Nt1较短时，随着水压差ΔP的增加而连续前进，其所对应的流速比Iμ亦随之逐渐增加，当达到0点附近（对应点在控制平面上位于分支曲线上）时，若此时陷落柱内作用于煤层底板的水压差稍有增加，则底板岩层将失稳破裂，渗流速度比Iμ将会剧增。当水压作用时间Nt1很长时，随着ΔP的不断增加，Iμ值连续增加达到突水区，而无突变现象，这是一种底板岩层随时间逐渐破坏而发生的突水过程。

假设陷落柱突水的突变模型为尖点突变模型，其势函数一般可由下式描述：

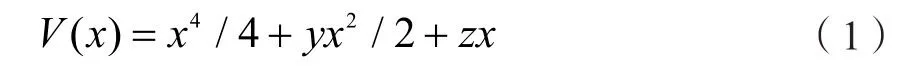
式中：

x，y，z-以Q为原点的坐标，如图3所示。

图3中平衡曲面的标准方程可表示为势函数的微分：

式（2）的判别式为：

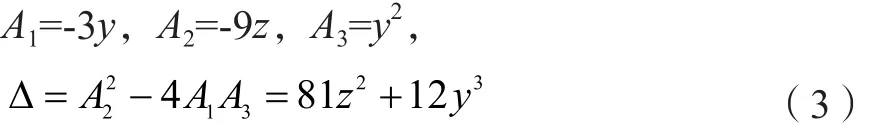
因此，控制平面内的分叉集为：

将标准方程的坐标旋转与平移至O(Iμ,MP,Nt1)坐标系中，有

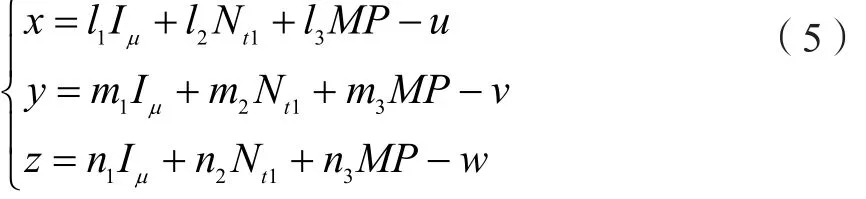
式中：

u，v，w-原点Q到O点的三维平移向量各分量；

li，mi，ni-新坐标的方向余弦，i=1，2，3。

由于Iμ轴与x轴平行，二者间的夹角为0，故方向余弦l1为：

联立式（2）～（6），可以得到平衡曲面在新坐标系下方程的表达式为：

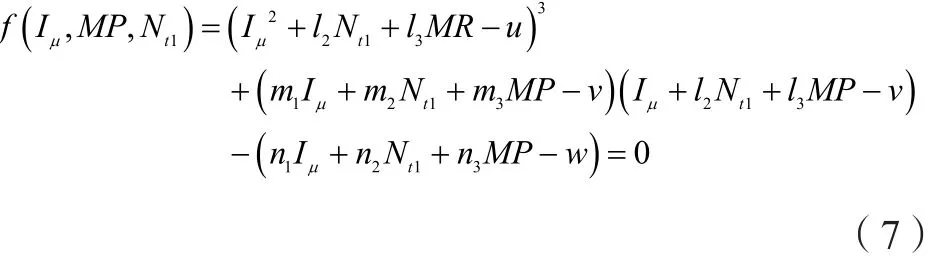
方向余弦之间是正交的关系，于是有如下结果：

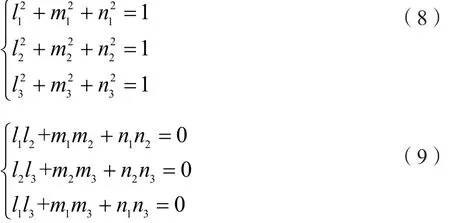
同为左手坐标系时，式（5）的系数矩阵的行列式为1，即：

模型的边界条件可以从所研究问题的物理意义获得。当无采动时，水压差ΔP=0，不同时刻的突水时间因子都位于Nt1轴上。用数学表达式表示曲面在该轴上的边界条件表达式如下：

又平衡曲面通过0点，故有：

把式（12）代入式（7），得：

由式（8）～（12）可得：

其中：

基于尖点突变模型的物理意义，尖点Q为分支曲线的交点，当底板状态趋向突水区越过Q点时，其渗流速度比Iμ＞1。因此，位于分支曲线交点Q处底板岩层中渗流速度比的界限值应为Iμ=1.0。在Q点平移至原点0的正上方时，相应的水压致突因子MP和时间因子Nt1皆为0，由式（5）可得：

把式（14）代入（7），得：

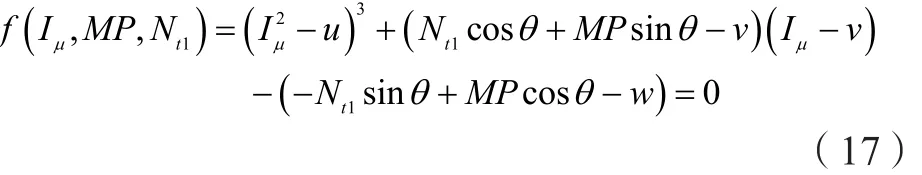
把式（13）、（15）代入（17），得：

至此，建立了渗流速度比、水压致突因子和时间因子三者间的关系，当底板的基本特性、含水层与煤层间的水压差和渗流速度已知的条件下就可以判断渗流突变时间以及渗流突变发生后速度的变化规律。

3 案例应用分析

地质勘探结果表明，司马矿陷落柱X3属于不充水型陷落柱，为避免工作面搬家，采用直接推过的方式处理。煤层底板距离奥陶系灰岩顶部约56m。随着工作面向前推进，底板水压力从天然状态的1.2MPa增加至4.3MPa，由此可知式（7）中的MP从0MPa/m增加至0.0554MPa/m。一般认为，当工作面进入陷落柱时，陷落柱受采动影响最为剧烈。记开采未影响陷落柱的时刻为0，则工作面进入陷落柱时刻Nt1=37d。根据第二部分所述，u=1，根据式（13）可得到v+w=1的结论。考虑到y轴和z轴与MP轴和Nt1轴夹角相等，那么有v=w=0.5。此时，对于式（18）而言，只剩下一个未知变量Iu。将以上数据代入式（18），可以反算出Iu值，得到Iu=0.72＜1，这意味着工作面推过司马矿陷落柱X3是安全的，为司马矿其余陷落柱的安全开采提供了理论支撑。

4 结论

本文由实际的陷落柱突水现象出发，分析了徐州张集矿、淮北桃园矿和淮南潘集二矿陷落柱突水的涌水量变化规律，发现这三次陷落柱突水事故中均出现了涌水量阶梯式快速增大，即渗流突变的现象，因此通过突变理论构建了渗流速度比、水压致突因子和时间因子三者间的关系，建立了陷落柱水害的尖点突变模型，并对司马煤矿陷落柱X3进行算例分析，该模型可以有效的解释陷落柱突变现象，对揭示陷落柱的突水机理具有十分重要的意义。