FRP约束普通和高强混凝土柱轴压性能的有限元分析

陈曦宸， 梁 军， 施鹏飞

（上海理工大学 环境与建筑学院，上海 200093）

由于结构尺寸和重量的限制，高强混凝土（HSC）越来越多地应用在建筑行业，其加固措施也受到相应的重视。与传统加固方法相比，纤维复合材料（fiber reinforced polymers/plastics, FRP）由于自身的优势，被广泛应用于各种结构或构件的修复和加固中[1-2]。现有的FRP约束混凝土轴压本构模型大致可分为两类：基于实验的设计型模型和基于数值的分析型模型[3]。然而大多数模型都是针对普通强度混凝土（NSC），在HSC方面还需要进一步的研究[4-5]。

随着计算机技术的发展，有限元方法（FEM）开始广泛应用于大型结构的数值模拟中，FRP约束混凝土的有限元模拟也成为可能。例如胡波等[6]和吴秋兰等[7]采用ANSYS分别模拟了FRP约束方形混凝土短柱和FRP约束混凝土圆柱的轴心受压性能。Piscesa等[8]采用ABAQUS模拟了FRP约束钢筋混凝土柱的轴压性能。最近，Lin等[9]通过三维有限元方法对FRP约束混凝土圆柱的偏压性质进行了研究，对有限元方法进行了改进。可以发现，数值模型中的一个重要挑战就是在模拟经度与计算耗时之间取得平衡[10]。Yu等[11]研究发现，对于长度大于等于两倍截面直径的混凝土柱，柱端约束对柱中的影响可以忽略不计。据此可以将全尺寸的混凝土轴压试样简化为一个薄片进行模拟，以缩短计算时间。

另外，纤维截面法也逐渐成为简化三维模型的有效手段之一。基于OpenSees[12]的纤维截面法可以将拥有不同材料性质的纤维截面集合到同一个有限元单元中，从而极大地缩短计算时间。OpenSees[12]是一个开放源代码的有限元平台，可以很方便地将各理论模型编制到其材料数据库中。王震宇等[13]基于OpenSees中的纤维约束混凝土模型，对FRP约束混凝土柱在水平荷载下的滞回曲线进行了有限元模拟。Wang等[14]和Ismail等[10]同样基于OpenSees对FRP约束钢筋混凝土柱的动力性能进行了模拟。

为了研究各种有限元方法的模拟精度和效率，本文采取ABAQUS的三维全尺寸模型、薄片模型，和OpenSees纤维截面模型进行有限元模拟。其中ABAQUS模型采用修正的混凝土压缩硬化曲线，OpenSees中的纤维截面模型则通过动态链接库（DLL）文件编制6个分析型FRP约束混凝土本构模型[4,15-19]。最后通过对比相关的实验数据，对各有限元方法模拟FRP约束NSC和HSC轴压性能的适用性进行研究。

1 模型描述

1.1 实验参数

为了对有限元模型结果进行验证，本文选取了文献[20]的FRP约束NSC实验数据以及文献[4]的FRP约束HSC的实验数据，实验参数见表1。表中：f ′co为混凝土强度；t和Efrp分别为FRP材料的厚度和弹性模量；εh,rup为FRP材料的极限应变；f ′cu和εcu分别为FRP约束混凝土的极限强度和极限应变。表中的实验条件均包含弱约束（W）、中等约束（M）和强约束（H）3种不同的约束等级，如弱约束普通强度混凝土写作W-NSC。实验试样均为混凝土圆柱，半径为152 mm，高度为305 mm，符合Yu等[11]提出的简化规则。需要注意的是，相同条件的轴压实验均包括两组实验数据，即原文中均进行了两次实验。

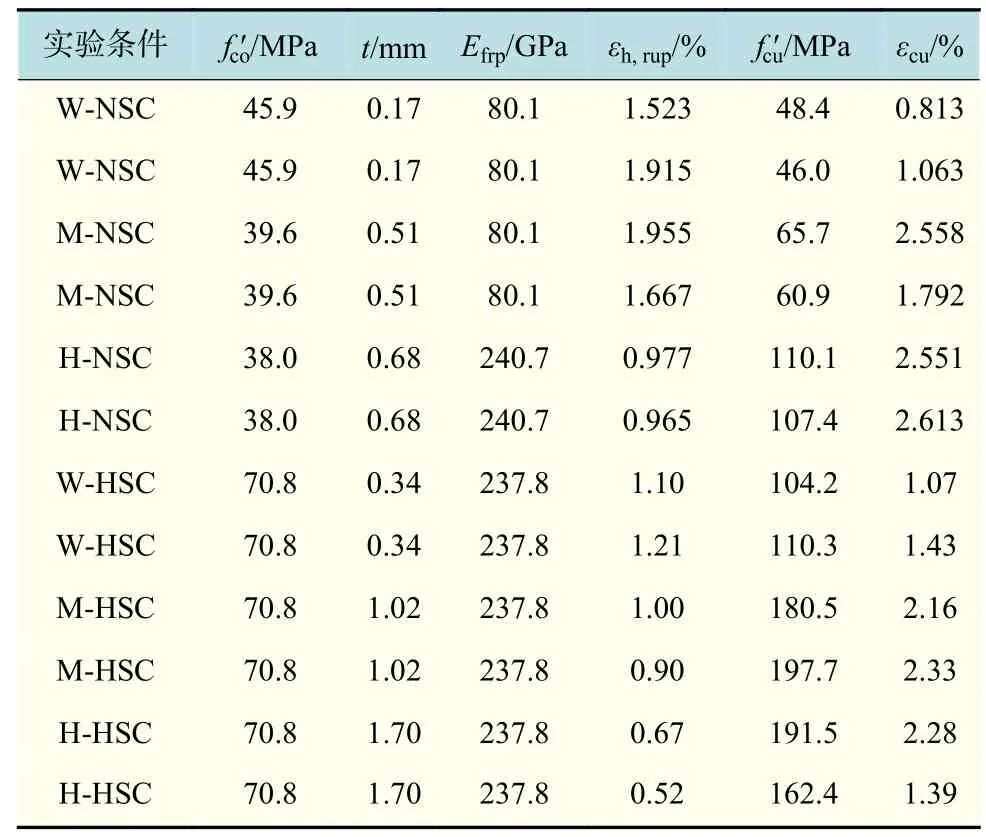
表 1 实验数据Tab.1 Experimental data used in the analysis

1.2 ABAQUS三维模型

1.2.1 模型尺寸和单元

ABAQUS中的全尺寸模型和薄片模型如图1所示。根据Hany等[21]的研究，FRP与混凝土之间的相互作用对结果影响不大，因此建模时通过“Tie Constraint”将FRP与混凝土表面的节点进行绑定。混凝土和FRP分别采用C3D8R和S4R单元进行模拟。由于模型和轴向加载条件的对称性，有限元模型只对试样的1/4进行建模计算，薄片模型则仅取全尺寸模型的一个横向切片进行模拟。x-z和y-z边界采用对称边界条件，分别对y和x方向的位移进行限制。全尺寸模型固定模型两端各方向的自由度，而薄片模型只固定轴向位移。两种模型均通过轴向位移进行加载。

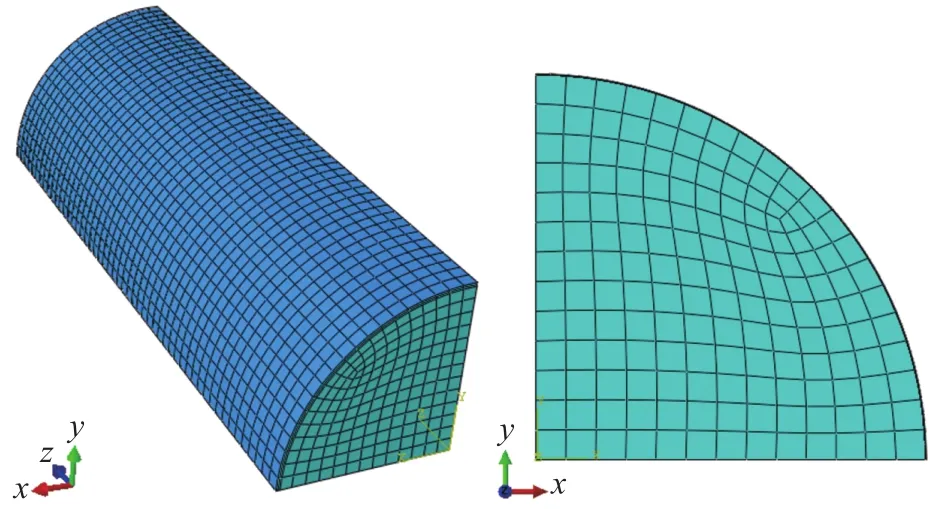
图 1 ABAQUS三维模型Fig.1 3D modeling in ABAQUS

1.2.2 ABAQUS模型的材料参数

教师也应当引导学生观察各种校内比赛和校内活动，让学生们不仅参与活动，获得更直接的体验感，积累更多具有体验感的素材，让学生在写作时更有热情和投入感。

FRP采用“LAMINA”弹性材料，其轴向的弹性模量E1= Efrp（见表1），泊松比设为零。其他性质，如各方向的弹性模量和剪切模量E2, G12, G13,G23，均取为 0.001 GPa。

混凝土的材料性质采用CDPM进行模拟，其弹性部分包含两个参数：弹性模量Ec和泊松比vc。其中Ec取自《美国FRP加固混凝土结构设计指南》（ACI 318）[22]，如式（1）所示。若无实验数据，vc则由Candappa等[23]的经验公式（式2）计算得到。√

CDPM的塑性性质则分为3个部分：拉伸性能、压缩性能和塑性参数。抗拉强度线性地取为0.1f ′co，且忽略拉伸破坏。塑性参数则取自Yu等[11]和Hany等[21]的修正CDPM材料。其中黏性系数取为10-7，偏心率取为0.1，其他3个参数膨胀角ψ、强度比fbo/f ′co和控制屈服面形状的参数Kc分别按下式计算：

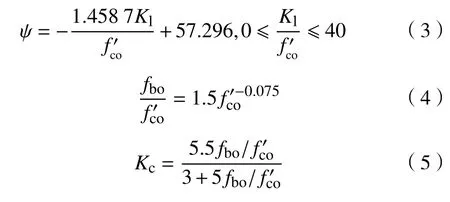
式中：fbo为混凝土双轴抗压强度；Kl= Efrptfrp/R为FRP材料的刚度；ψ的取值范围限制在0.1～56。

混凝土的压缩性能分为压缩硬化和压缩破坏两部分。与拉伸破坏类似，这里不考虑压缩破坏的影响。压缩硬化性质需要输入未约束混凝土的应力应变散点进行设置。而一些研究表明[11]，原始的未约束混凝土应力应变曲线并不适用于模拟FRP约束混凝土。因此，基于Hany等[21]的研究，本文提出一个修正的未约束混凝土应力应变模型。该模型将FRP提供的侧向围压作为ABAQUS运算过程中的环境变量。模型曲线分为两段，峰值前取为Popovics[24]的理论曲线，峰值后则采用Xiao等[4]的模型。同时，未约束混凝土的峰值应变ε′co在约束压力不断提升的过程中增加为约束混凝土的峰值应变ε′cc。曲线后半段中，根据Xiao等[4]的模型得到的轴向应力fc则都减去约束混凝土和未约束混凝土的峰值应力差（f ′cc-f ′co）。由此所得新模型的表达式为

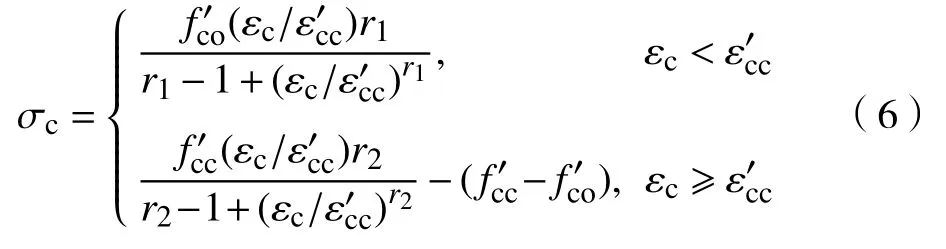
式中：σc为轴向应力；εc为轴向应变；峰值应力f ′cc、峰值应变ε′cc，以及参数r1，r2的计算为

式中，σl是作为环境变量的围压。

由于ABAQUS中的CDPM材料需要输入非弹性应变和相应的应力作为数据点，在计算过程中取f ′co/2对应的应变为弹性应变。图2所示（见下页）为表1中M-NSC据以上模型得到的修正压缩硬化曲线。

图 2 原始和修正压缩硬化曲线Fig.2 Original and modified compressive hardening curves

本文选取了 Teng 等[18]、Cui等[16]、Xiao 等[4]、Dong等[17]和Lim等[19]5个分析型FRP约束混凝土本构模型，并采用C++语言编制的DLL文件将其添加到OpenSees的材料库中。另外，OpenSees现有的FRP约束混凝土材料[12]是基于Spoelstra等[15]的模型编制的，这里将其重新编制，并与所选取的模型进行对比。

如图3所示，纤维截面模型极大地简化了ABAQUS的三维模型。该模型只有一个双节点的梁单元，且可以在环向和径向嵌套拥有不同材料属性的纤维截面。在受力过程中，各截面没有相对滑移地协同工作。

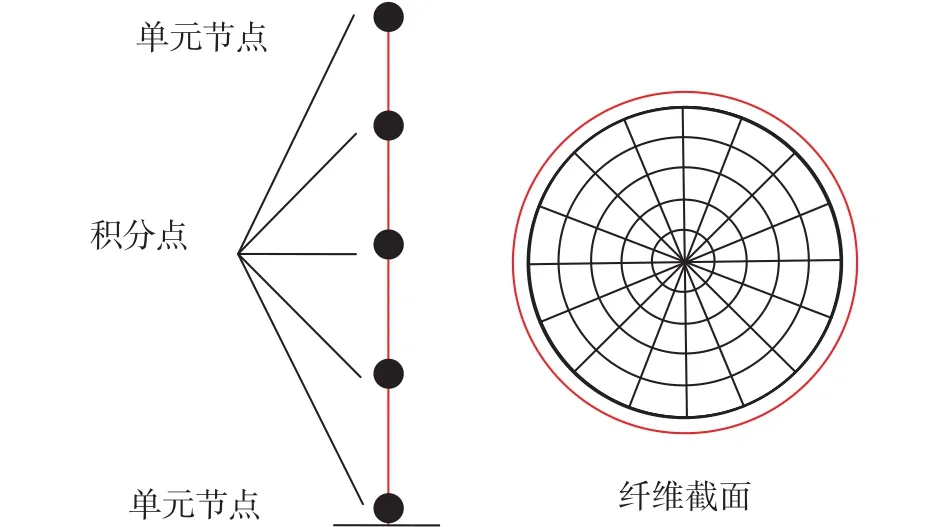
图 3 基于OpenSees的纤维截面模型Fig.3 Fiber section model based on OpenSees

OpenSees的单元库提供了3种可用的梁单元 ： forceBeamColumn， nonlinearBeamColumn 以及dispBeamColumn。通过对比模拟结果可以发现，三者对结果几乎没有影响。此外，积分点和纤维截面的数量越多，计算耗时越长，但对单元的力学性能影响也很小。因此，后文的模拟均采用nonlinearBeamColumn单元，积分点和纤维截面的数量均取最小值2。基于这些设置，总体的计算时间可以限制在1 s以内。

2 结果对比

2.1 ABAQUS模拟结果

对比全尺寸模型和薄片模型的模拟结果可以发现两者之间的差距很小。图4和图5分别为HNSC和H-HSC的应力应变（）曲线和横向应变-轴向应变曲线（）。可以发现，全尺寸模型的应力应变曲线（如图4（a）和图5（a）所示）略低于薄片模型对应的曲线，而全尺寸模型的横向应变-轴向应变曲线（如图4（b）和图5（b）所示）则略高于薄片模型对应的曲线。两类模型都可以很好地反映实验值，其中薄片模型对应的曲线与实验曲线更加贴合。

图 4 ABAQUS对H-NSC的模拟结果Fig.4 ABAQUS simulation results for H-NSC

2.2 OpenSees模拟结果

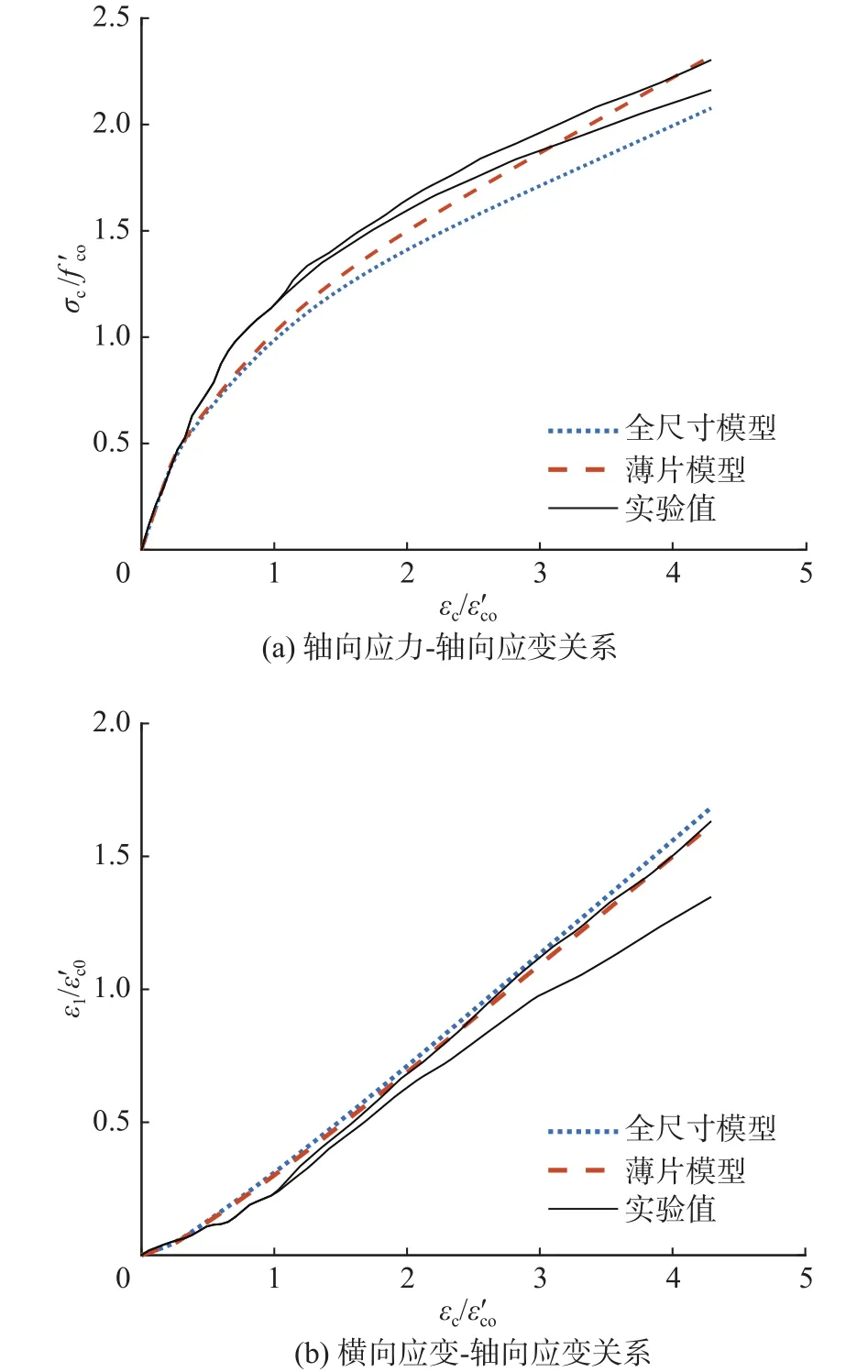
图 5 ABAQUS对H-HSC的模拟结果Fig. 5 ABAQUS simulation results for H-HSC

采用OpenSees的纤维截面法模拟的W-NSC和W-HSC结果分别如图6和图7（见下页）所示。由图可以看出，所有模型都能很好地模拟曲线转折点以前的部分，模型误差主要出现在曲线后半段。模拟结果的准确性也很大程度上依赖于所采用的FRP约束混凝土本构模型。例如基于Lim等[19]的模拟结果与实验曲线在各种条件下都非常贴合，而基于Spoelstra等[15]的模拟曲线则只有WHSC情况下的应力应变曲线表现出较好的准确度。从图6（b）和图7（b）可以看出，各模型均低估了FRP约束混凝土的横向应变，其中Spoelstra等[15]以及Cui等[16]的模型误差最大。

2.3 模拟精度对比

各有限元模型的模拟结果可以用均方根偏差（RMSD）来表示，即

图 6 OpenSees对W-NSC的模拟结果Fig. 6 OpenSees simulation results for W-NSC

式中：Pi为实验值；Si为模拟值；n为数据点的个数。RMSD越小表明模拟结果越准确。后面对εl/ε′co和σc/f ′co进行了考察，由于每个实验条件都有两组实验结果，最终的RMSD取其平均值。

表2（见下页）列出了ABAQUS全尺寸模型和薄片模型对应的RMSD。其中：实验条件NSC和HSC分别表示所有约束强度下的NSC和HSC；NSC-HSC表示将两种混凝土强度下的数据结合起来，平均值则表示该条件下εl/ε′co和σc/f ′co对应RMSD的平均值。通过表2可以发现，除了MHSC条件下的εl/ε′co外，薄片模型的RMSD均低于同条件下的全尺寸模型。这表明薄片模型的模拟结果在大部分条件下都比全尺寸模型更加准确。观察NSC和HSC两个实验条件可以发现，HSC对应的RMSD均低于NSC，表明ABAQUS模型更适于模拟HSC。考察约束强度的影响可以发现，随着约束强度的升高，εl/ε′co对应的 RMSD越来越小，而σc/f ′co对应的RMSD则表现出增加的趋势。由此可知，ABAQUS模型在模拟弱约束下的应力和强约束下的应变时具有更高的准确度。此外，各模型对应的RMSD普遍低于表明ABAQUS模型对的计算更加准确。

图 7 OpenSees对W-HSC的模拟结果Fig. 7 OpenSees simulation results for W-HSC

表 2 ABAQUS模拟结果对应的RMSD Tab.2 RMSD values for ABAQUS results

表3为OpenSees各模型所对应的RMSD。由于Spoelstra等[15]和Cui等[16]的模型误差较大，表3只列出其他4个模型的结果。由于文献[18]和文献[4]都采用了Teng等[18]的横向应变-轴向应变曲线，其对应的RMSD也相同，因此表中只列出Teng等[18]对σc/f ′co的RMSD。通过观察NSC-HSC条件下的数据可以发现，Xiao等[4]和Lim等[19]分别对σc/f ′co和εl/ε′co的RMSD去最小值，且其对应的平均RMSD也最低，表明这两个模型最适于模拟FRP约束NSC和HSC的受力和变形性能。考察混凝土强度的影响可以发现，大多数模型对应HSC的RMSD均低于NSC，表明这4个模型都能较好地模拟FRP约束HSC的材料性质。考察约束强度的影响可以发现与ABAQUS相似的现象，即随着约束强度的升高，εl/ε′co对应的RMSD越来越小，而σc/f ′co对应的RMSD则越来越大。同样地，各模型对应σc/f ′co的RMSD普遍低于εl/ε′co，特别是基于Xiao等[4]的纤维截面模型，表明OpenSees模型对σc/f ′co的计算更加准确。

表 3 OpenSees模拟结果对应的RMSDTab.3 RMSD values for OpenSees results

最终，结合表2中ABAQUS的模拟结果和表3中OpenSees的模拟结果可以发现，ABAQUS的薄片模型在综合模拟NSC和HSC的应力和应变时的准确度最高，其次为基于Lim等[19]和Xiao等[4]的 OpenSees纤维截面模型。其中 Xiao等[4]和Lim等[19]对应的模型分别在单独计算轴向应力和横向应变方面具有优势。

3 结论与建议

本文基于ABAQUS和OpenSees有限元平台对FRP约束NSC和HSC的轴压性能进行了研究，对比分析了各模拟方法的准确性。其中ABAQUS有限元模拟中的混凝土破坏塑性材料模型采用了修正的压缩硬化模型，并对全尺寸模型和薄片模型进行了对比。OpenSees中的纤维截面模型则通过C++编制的DLL文件，引入了6个分析型FRP约束混凝土本构模型。主要结论如下：

a. 修正的CDPM压缩硬化模型（式（9））提高了ABAQUS有限元方法模拟FRP约束NSC和HSC的精度。

b. ABAQUS中的全尺寸模型和薄片模型模拟结果相差不大，其中薄片模型计算耗时更少，精度也稍高。

c. OpenSees纤维截面模型严重依赖其所依据的分析型模型，其中Xiao等[4]和Lim等[19]对应的模型模拟精度较高。另外，纤维截面和积分点的数量对结果的影响并不大。

d. 综合对比模拟精度和计算时间，基于修正压缩硬化曲线的ABAQUS薄片模型最适合FRP约束NSC和HSC的有限元模拟。