转子时间常数对FOC系统的影响分析及解决方法
2018-09-21何国锋
肖 杰 潘 峰 何国锋
(1.茅台学院实习实训中心,贵州遵义564507;2.茅台学院酿酒工程自动化系,贵州遵义564507)
0 引言
感应电机采用磁场定向控制来调速,一般需要通过间接磁链观测器来估算转子磁链[1],这种间接观测方法却易受电机众多自身参数影响,其中转子时间常数影响最为严重,这导致整个磁场定向控制系统的瞬态响应性能降低。但是,当前离线辨识方法不能准确测定出转子时间常数,而且增加了额外步骤和不稳定因素。即使辨识准确,在电机运行过程中,电机参数也容易受温度和频率等因素影响而改变。针对上述情况,本文基于模型参考自适应系统对转子时间常数进行在线辨识,保障系统运行参数的实时性和准确性,提高系统整体稳定度。
1 转子时间常数对系统的影响性分析
磁场定向的准确性是感应电机转速和转矩瞬态响应性能好坏的重要决定因素,而磁场定向不可避免地需要将励磁电流和转矩电流完全分离开来。分离过程需要许多电机参数参与运算,这些参数对分离的效果有着至关重要的作用,其中电机的转子时间常数影响最为重大[2]。
感应电机模型在旋转坐标系下,转子磁链与电压方程为:

式中,ψr、Lm、Lr、is、ir、Δω、Rr分别为转子磁链、互感、转子自感、定子电流、转子电流、转差角频率、转子电阻。
联立等式(1)和(2)并整理有:

将带有偏差量的磁链代入式(3),并将磁链变为dq轴分量形式,则有:

由磁场定向调速的相关性质可知[1],若磁场定向方式采用转子磁链定向,且为速度闭环则有:
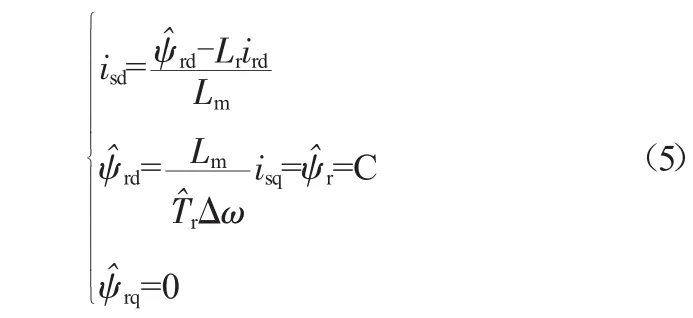
式中,isd、isq为定子电流在dq轴系上的分量;C为常数。
联立等式(5)和(4)并整理后有:
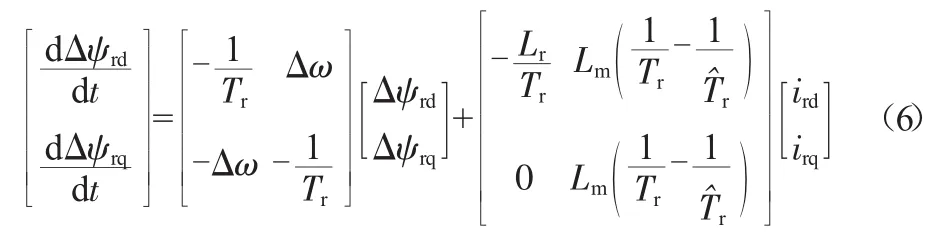
可得微分方程组(6)的特征值为:

系统无阻尼振荡角频率为:

阻尼系数为:

由等式(8)与(9)可知,带有因为转子时间常数变化而造成磁链偏差量的磁场定向系统,为按指数(e-ξωnt)规律衰减的振荡欠阻尼系统[3]。此外,磁链和转矩之间相互影响,则电机的转速和转矩也会具有相同的波动规律,影响电机的平稳高效运行。
2 转子时间常数的在线辨识
2.1 模型参考自适应
感应电机数学模型是一个异常复杂的控制模型且参数变量多变难以控制,模型参考自适应控制系统(ModelReference AdaptiveSystem,MRAS)为这类多变量系统提供了很好的解决方法[4],该方法运算简单但却具有很好的控制效果。
MRAS通常由三大模块构成:第一个模块由不包含估计参数的参考模型构成,第二个模块由包含估计参数的可调模型构成,第三个模块为自适应机构。其中,前两个模块一般要具有相同的物理含义,且前两个模块的输出偏差作为自适应机构的输入,最后经过自适应机构的处理,将输出反馈给可调模型,使得估计参数不断逼近真实参数。波波夫(Popov)稳定性能使系统偏差逼近于零[5],从而MARS最终达到全局稳定,避免因偏差的累计而受到影响,故本文以波波夫超稳定性理论依据来推导模型参考自适应系统的数学模型。
2.2 转子时间常数在线辨识数学模型
如图1所示,转子时间常数在线辨识数学模型以转子磁链为基础,参考模型选用转子磁链的电压模型,可调模型选用转子磁链的电流模型,波波夫超稳定性理论作为自适应律。
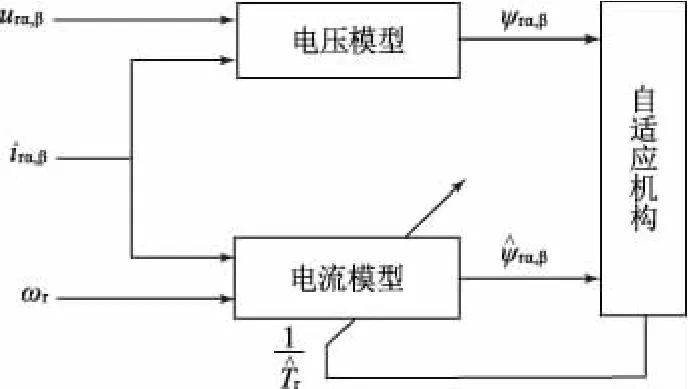
图1MRAS基本构成框图
电流模型和电压模型的数学表达式如下:
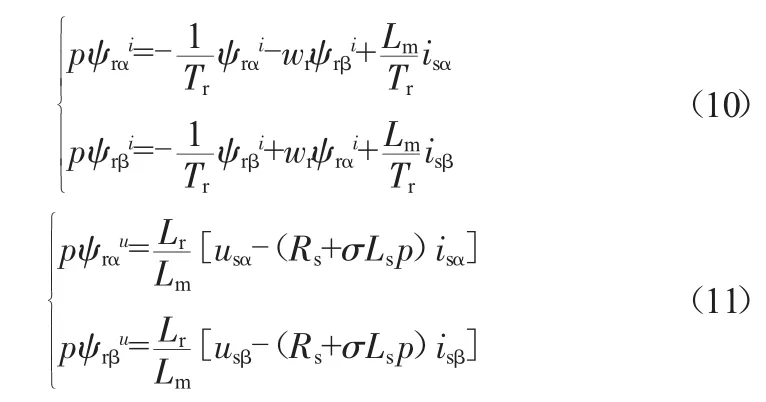
将估算出的Tˆr代入等式(10)得到电流模型的转子磁链估算表达式:
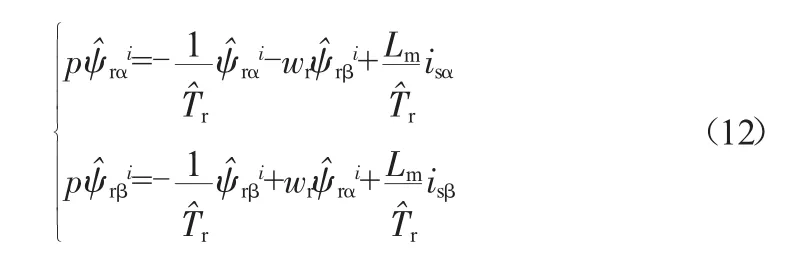
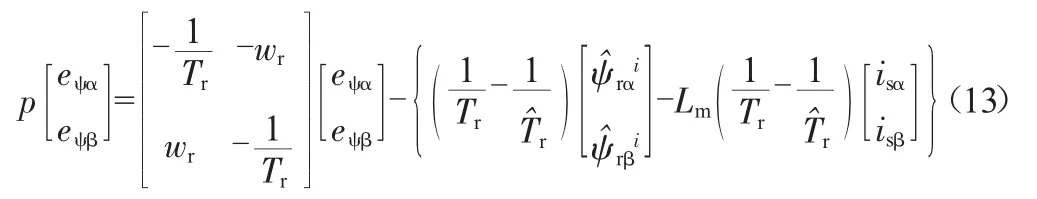
上式状态变量系数矩阵为线性前馈环节,其余项为非线性反馈环节。分析可知状态方程(13)的线性环节严格正实,并且状态方程(13)的非线性环节满足波波夫积分不等式的要求[5]。此时,系统的自适应律为:
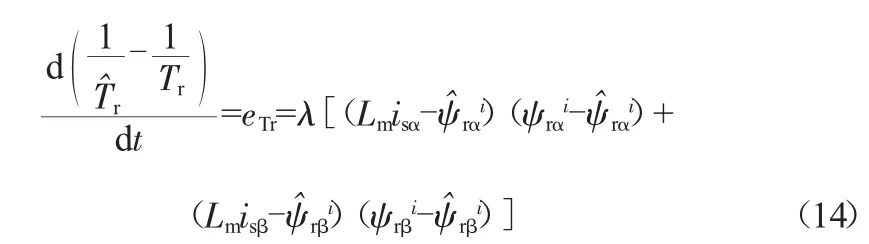
实际操作中,为简化调节步骤,提升动态性能,将等式(14)自适应律转换成PI调节形式。
同时,由于转子时间常数没有参与电压模型的运算,所以将电流模型的转子磁链真实值用电压模型估算出的转子磁链来替换。
则推出最终转子时间常数的估计式:

基于MRAS的Tr在线辨识模块如图2所示。

图2 Tr在线辨识模块
3 仿真分析
为验证Tr的影响性数学推导分析和该在线辨识方法的正确性,利用Matlab/Simulink搭建了一套基于磁场定向控制的Tr在线辨识系统。仿真选用的感应电机额定参数为:Pn=4kW,Un=400V,In=8.8A,Nn=1430r/min,RS=1.405 Ω,Rr=1.395 Ω,Lσ=5.839mH,Lm=0.1722H,Tr的倒数为4.023 Ω/H。
3.1 转子时间常数的影响性仿真结果分析
将电机的Tr放大3倍,待电机运行1s,电机稳定运行后,加入10N·m负载转矩,电机的转速和转矩仿真波形如图3所示。

图3 Tr放大3倍后的影响性分析
从图3波形可知Tr的变化导致电机的转矩与转速瞬态响应迟缓,幅值以相同频率衰减振荡并逐渐趋于稳定。
3.2 转子时间常数在线辨识仿真结果分析
Tr在线辨识算法的正确性可从阶跃性能和跟踪性能来进行验证。分别模拟电机启动时转子时间常数初始值未知和电机在运行过程中转子时间常数突变两种情况。
3.2.1 阶跃性能
转子时间常数初始值放大两倍时,电机以1000r/min给定值匀速运行至4s时,加入20N·m负载。在线辨识算法辨识所得转子时间常数的倒数波形如图4所示。

图4 =2Tr时的阶跃性能波形
分析该辨识算法的阶跃性能波形可知,转子时间常数辨识误差小,加入负载时,动态调节速度快。此外,启动给定数值偏离实际数值越大,趋于稳定的时间就越长,所以转子时间常数离线辨识的准确性一定程度上影响了在线辨识算法的收敛速度。
3.2.2 跟踪性能
电机以1000r/min给定值匀速运行至4s时,突然将电机转子时间常数放大两倍。此时,在线辨识算法辨识所得波形如图5所示。

图5 2Tr时的跟踪性能波形
4 结语
本文先通过转子时间常数对磁场定向控制系统影响的数学推导分析,说明转子时间常数的准确性对系统动态性能效果的重要性。接着,引入基于模型参考自适应的转子时间常数在线辨识算法,解决了离线辨识算法存在的现有问题。从影响性分析仿真结果可知该辨识方法具有较好的实时性和准确性,能够应用于磁场定向调速系统的转子时间常数在线辨识。
