大规模时序图数据的查询处理与挖掘技术综述
2018-09-21王一舒王国仁
王一舒 袁 野 刘 萌 王国仁
1(东北大学计算机科学与工程学院 沈阳 110004) 2 (北京理工大学计算机学院 北京 100081) (yishuwang@stumail.neu.edu.cn)
近年来,随着语义网络(semantic Web)、社交网络(social networks)、生物网络(biological networks)等新兴领域的飞速发展,数据的结构越来越复杂,数据量呈几何状增长,并且这种增长趋势还在不断的持续[1].图(graph)作为一种特殊的数据存储模型,在大规模数据中的应用越来越广泛,实现对复杂数据的存储和分析.图作为一种抽象的数据类型,从概念上可以分2种类型:有向图(directed graph)和无向图(undirected graph).每个图数据结构包含了一组顶点(vertices)用来表示对象,顶点间由有向或者无向的边(edges)连接,用来表示对象与对象之间的二元关系.在实际应用中,图的顶点和边上常常带有特定的信息,像标签或者数字属性等(如长度、花销等).例如,用图来表示一个城市之间的到达关系,其中每个顶点表示一个城市,若2个顶点之间存在边,则表示2个城市之间是可以直接到达的,在这种情况下,边上会有用来表示2个城市之间距离信息的标签.随着图上的研究不断深入,研究者们发现有些网络会随着时间不断变化,例如在上面的例子中,若在边上加上表示时间的标签,那么就可以表示该城市的公交车辆运输网络,边上的时间表示这条道路上公交车的起始时间.如何在这类随时间变化的图上进行查询处理与挖掘工作成为了当前热门的研究领域,为了更好地为这类随时间变化的图构建模型,研究者们提出了一种新型的图模型——时序图.
时序图(temporal graph,也被称为temporal net-work[2-3],time-dependent network[4],time-varying graph[5])是一种会随着时间不断变化的图结构.时序图本质上是带有随时间变化标签(label)的图,即图中的标签带有某种特定的时间属性.与强调维护查询处理与挖掘结果正确性的动态图(dynamic graph)和对过去快照(snapshot)进行查询的历史网络(historical network)不同,时序图强调在一个时间阈值内数据的变化.时序图的应用非常广泛,许多网络模型都可以通过时序图来构建模型,或者说只要存在动态逻辑的图都可以通过时序图建模和研究.常见的时序图应用有5个方面:
1) 点对点通信
点对点的通信(如信息或电子病毒的动态传播)是一种一对一的消息传播形式,这种消息传播形式非常符合时序图模型.点对点通信通常分为2种情况:①在某一时刻上将一系列信息从一个人传播到另一个人,持续时间可以忽略不计,如电子邮件、手机短信或者在线论坛等即时的消息网络;②在一个时间段上2个人之间的消息传播,如打电话,这种情况虽然不是即时的,但是有特定的持续时间[6-8].但是在很多情况下这段持续时间可以被忽略不计,在这种情况下打电话就可以被认为是即时的.
2) 一对多的消息传播
与一对一的通信网络不同,一对多的消息传播形式更多是强调单一个体对一个群体进行消息的传播,即消息以广播的形式扩散,最常见的一对多的传播形式是微博和朋友圈.现有的研究大多还没有将时间维度作为一个考虑因素,但是Yasseri等人在文献[7]中分析维基百科的编辑们活动的作息规律时,引入了时间维度来估计编辑们的地理位置.
3) 生物信息网络
常见的生物信息网络包括:基因调控网络(gene regulatory networks)、代谢网络(metabolic net-works)、信号传导网络(signal transduction pathway)以及蛋白质互作网络(protein-protein-interaction networks),很多情况下这些细胞中分子的相互作用都可以通过图来构建模型.现有的大部分研究工作都是在静态图上进行的,但是在真实世界中,许多生物功能中的连接不是一直处于活跃状态的,Przytycka等人[9]认为在未来的工作中从静态网络分析提升到动态网络分析是必不可少的,而现在也有一些工作开始考虑时间对蛋白质互作网络[10]和基因调控网络[11]的影响.
4) 道路交通网络
道路交通网络是指各种运输网、邮电网构成的整体交通网.道路交通网络通常有一些固定的网络路线,有一组运输单位在这些路线上随时间不断地改变位置.道路交通网络可以说是最适合用时序图建模的网络之一,因为很多情况下,在道路交通网络上时间本身就是一个必须考虑的因素,例如航班运输网络中,当需要转乘航班时,转乘航班的起飞时间必须在转乘之前的航班到达之后,才能保证转乘成功.文献[12]就是以火车行程表为例,给出了在时序图上的可达性查询和基于时间的路径查询方法.
5) 在线社交网络
在线社交网络如Facebook,Twitter等通过记录用户的数字轨迹来研究相关信息.在社交网络中,仅使用用户之间的关注信息和好友关系来确定用户之间的密切程度是不够的,还需要记录他们之间更为具体的互动,才能更加精确刻画用户之间的关系,而时间是常见的影响因素之一,所以考虑时间的影响是十分必要的.例如在社交网络中,通常用时间戳(time stamp)来记录用户的上线和下线操作;当一个用户关注另一用户时,也会存在一个时间戳来记录这种操作;同理,当用户取消关注时,这个行为也会被时间戳记录下来.
现有的绝大多数图查询处理与挖掘技术都是应用于静态图(static graph)和动态图上的,研究者们提出了大量的查询和处理方法来解决图上数据查询处理与挖掘时可能遇到的问题.但是,由于时序图上考虑了时间影响,所以时序图上的查询要比静态图上更为复杂,如在静态图上最简单的最短路径查询,在时序图上就要更为细致地考虑在某一时间阈值内的最短路径.同理时序图上的挖掘问题也需要考虑时间对挖掘结果的影响,如最小生成树问题,在时序图上需要考虑满足特殊时间条件的最小生成树.而且许多静态图上可以在线性时间内解决的问题,在时序图上会成为NP完全或者NP难问题,如连通分支问题.而在动态图上,虽然存在着随着时间变化的动态图,但是这些动态图上的方法主要是用来维护图上的查询处理与挖掘的增量结果,例如动态图上的可达性查询问题是要提出一种方法来维护2个顶点之间的可达性,而时序图则是要判断在给定时间内,2个顶点是否是可达的.而动态图上也可以在P时间内解决的问题,在时序图上确是NP问题,如最小生成树问题.因此与动态图相比,时序图上的查询处理和挖掘问题的定义和解决的目标不尽相同.所以随着时间因素的引入,现有的静态图和动态图上的方法并不能很好地适配于时序图上,这为时序图上的查询处理与挖掘工作带来了巨大的挑战.为了解决这些问题,一些基于时序图上的查询和处理方法相继被提出.

Fig.1 Difference between static graph and temporal graph, and the time sequence of temporal graph图1 静态图和时序图的区别以及时序图中的时间序列
1 时序图数据定义与模型
图是一种数学对象,现实生活中的许多动态系统上的问题可以通过图来解决,比如社交网络上消息的传播、网络上包的传输等,但是其实这些动态系统(如社交网络,传输网络等)才是研究者们真正感兴趣的东西[13].动态系统建模最大的优点在于,它不需要去考虑这些动态系统上实际的动态,只需要考虑动态系统上的行为.即动态系统可以估计网络上部分与部分之间的影响;也可以计算动态系统的优化程度;还可以查找在系统操作中哪些顶点有相同的作用等[14-17].但是动态网络的变化多种多样,为了更好地构建模型,研究者们将其中按照时间变化的动态网络建模成时序图,如将时间作为边上的权值(weight),通过时间序列来表示顶点和边之间的连接和交互关系.如图1所示,图1(a)表示有4个顶点的静态图;图1(b)表示存在于1~10时间阈值内的时序图;图1(c)表示图1(b)中顶点和边对应的时间序列.在静态图1(a)中,如果顶点A与顶点B相连,而顶点B与顶点C相连,那么A和C之间一定存在一条经过B的路径使得A和C之间是连通的.但是在时序图1(b)中如果A和B之间的边(A,B)存在于时刻{6,8,9},而B和C之间的边(B,C)存在于时刻{2,4,6},那么只有在时刻6时A和C是通过B连通的.因此,在时序图中,时间是一个非常重的影响因素,顶点与顶点之间的关系也随着时间不同在不断地变化,这使得不同时间阈值内图的结构是完全不同的.因此静态图上的定义和模型并不能直接适用于时序图,下面本文将给出时序图的基本定义和常见的模型.
1.1 时序图基本定义
给定一个时序图G=(V,E),其中V是G中的一组顶点,E是G中的一组边.对于一条边e∈E,用四元组(u,v,t,λ)来表示,其中顶点u,v∈V,t是起始时间(starting time),λ是从u到v遍历时间(traversal time),则从u到v的终止时间(ending time)为t+λ.边e的起始时间为t(e),遍历时间为λ(e),即e在[t,t+λ]时是被激活的.
时序图可以分为2种情况:1)顶点间的相互作用.是指在一个确切时间上发生的、持续时间可以忽略不计的时序图,即λ(e)=0.在这种情况下,时序图可以用三元组(u,v,t)表示,对于e存在一组时间序列Te={t1,t2,…,tn}作为标签.这种时序图常用来表示邮件网络、电话网络、信息网络等即时通信网络或者持续时间不重要的网络.2)时序图中的边在时间阈值中被激活,即λ(e)≠0.这种时序图常用来表示持续时间很重要的时序图,例如在道路交通网络中,常用这种时序图来表示飞机运输网络,用顶点表示机场,顶点间的边表示2个机场之间存在航班,边上时间的标签表示在标签时间时有飞机经过.虽然,时序图上部分拓扑结构的性质与静态图类似,如顶点的定义.但是由于时序图引入了时间标签,顶点与顶点的关系将会受到时间影响,所以一些图上的基本拓扑性质不能直接引用静态图上的定义,而动态图上很多拓扑性质是不能被定义的,只能根据动态图的性质提出信息维护方式来找到这些性质.下面本文将根据静态图上的定义,给出常见时序图上的拓扑性质定义.
顶点之间的连通性(connectivity)是图中最基本的概念之一,连通性是指一对顶点之间是否存在一条路径使之连通.任何图都可以根据其连通性划分为若干组顶点;这些划分反过来又为图上发生的动态操作施加限制.而对于静态图,顶点分为连通的和不连通的,连通分量(connected component)被定义为顶点之间存在的路径点集.而在有向图中,连通分量分为2种情况:强连通分量(strongly connected component),即所有顶点对之间都存在一条有向的路径和弱连通分量(weakly connected component),即假设边是无向的,所有顶点之间都存在一条路径.这2个概念可以推广到时序图中.对于时序图G,当顶点u和顶点v之间存在一条基于时间的有向路径,则2个顶点是强连通的;当顶点u和顶点v之间存在一条基于时间的无向路径,则2个顶点是弱连通的.
在静态图中,顶点之间的距离(distance)是指2个顶点之间的最短路径长度;在时序图中,顶点之间的距离是指2个顶点可达的最短时间.在静态图中,图的直径(diameter)是指任意2个顶点距离最大值;在时序图中,2个顶点不是在任意时间都是连通的,因此时序图的直径是最小的顶点距离,以此来保证在时序图G的激活时间内,不会有过多的顶点距离小于直径.
1.2 时序图模型
当时间是离散的,时序图可以简化成为一个边e∈E上的标签都为0或常数的静态图G=(V,E).边上的标签表示边被激活(available)的时间,即边上的标签为0表示这条边永远不会被激活,而当边上的标签为常数时,表示这条边在该常数时刻是被激活的.这里的标签可以是秒、天、年等,也可以是一些人为且离散的时间度量形式.本文将根据时序图的特点,介绍3种常见的时序图建模形式.

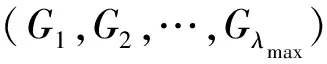

Fig.2 Graph transformation from temporal graph to static graph图2 时序图转化为静态图实例
第3种是通过时间为顶点构建副本,将时序图完全地转换成静态图.现有图上的查询处理与挖掘方法都是在静态图上完成的,大量的静态图上的数据查询处理与挖掘被提出,并且技术已经趋于完善,如果能在不丢失任何信息的前提下,将时序图转换成与之等价的静态图,为时序图上的查询处理与挖掘工作提供良好的基础.时序图转换静态图的基本思想是:根据边上的时间信息为每个顶点创造多个副本,即在同一个时刻的图中同时存在顶点和顶点的多个副本,通过顶点副本将时序图转化为静态图.对于时序图G=(V,E)和静态图G=(V,E),V={v1,v2,…,vn},则V={(vi,t):1≤i≤n,1≤t≤λ(e),vi=vi}.根据时间戳将图G水平分层,在每个水平层次包含V的副本,然后根据时间添加顶点与顶点副本之间的边,并规定边只能从上层顶点指向下层顶点,即顶点(vi,t),1≤t<λ(e)和它的一个副本(vi,t+1)之间存在边e=((vi,t),(vi,t+1)).这种方法通过完全保留顶点之间传递信息的方式,将顶点间的信息存储下来,但是在某些特定情况下,有些边可以被省略[18].图2是一个将时序图转换成静态图的实例.图2中(a)表示一个时序图G,每条边的持续时间为1;图2(b)表示由G以顶点a为原点,保留所有路径和时间信息转换成为静态图G.这种建模方法可以使静态图上的方法完美移植到时序图上,这也是现有时序图上常见的建模形式,但是随着大数据时代的到来,图的规模不断扩大,稠密且大规模的图数据不断增多,这种方法使图的规模激增,因此这种方法不能很好地应用于大图数据中.
2 时序图数据查询处理方法
静态图的拓扑结构可以通过大量的特征信息来度量[19],这些特征信息一般是基于顶点之间的邻接关系(如顶点的度或聚类系数)或者较大的顶点集合之间的连接关系(如网络直径).这些特征信息的度量方式在静态图中已经非常成熟,有些方法只需要稍作改变就可以直接应用到时序图中,如时序图中顶点的度是由某一时间时间阈值内激活的边的数量决定的.但是大部分的方法并不能很好地适应时序图,如时序图中路径是随时间不断变化的,若想要研究2个顶点之间的路径,要考虑时间先后对路径的影响.下面本文将介绍4个时序图上已经提出的查询处理问题.
2.1 时序图上路径问题
图上顶点间的路径(path)表示连接顶点的一条通路.路径问题是最基本查询问题之一.在静态图中,路径是从一个顶点出发,到另一个顶点为止的一组边.最短路径查询是最常见的关于路径的查询.在静态图上最经典的最短路径查询算法是Dijkstra[20]算法.文献[21]提出了一种2-hop算法,这种方法为图中每个顶点构建索引,记录该顶点能在2跳内到达的顶点,当查询2个顶点之间的最短路径时,只需要查找这2个顶点的索引即可.文献[22]列举了大量的最短路径算法,并通过实验对这些方法进行了分析和比对.但是在时序图中,要想找到顶点间的路径必须考虑路径边上激活时间的先后顺序.因此在时序图中,路径通常被定义为连接顶点集的非递减连续时间的一组边的序列,在文献[23-24]中这种路径被称为“依赖时间(time-respecting)的路径”.
时序图上的路径查询比静态图上的路径查询更为复杂,简单的求2个顶点间的最短路径已经不能满足时序图上的查询需求.在时序图上,路径问题要考虑2个部分:时间和路径长度.经典的时序图上的路径问题有最早到达路径(earliest arrival path,EAP)、最迟离开路径(latest departure path,LDP)和最短持续时间路径(shortest duration path,SDP)[25].
1) EAP问题
EAP问题是指给定2个顶点u和v和起始时间戳t,求从顶点u出发到达顶点v的需要的最短时间,即求从站A到达站B所需的最短时间和应该选择的路径.
2) LDP问题
LDP问题是指给定2个顶点u和v的终止时间戳t′,求若在时刻t′之前从顶点u出发到达顶点v,最迟从顶点u出发的时间,即如果计划在时刻t′之前到达站B,求最晚从站A出发的时间和应该选择的路线.
3) SDP问题
SDP问题是指给定2个顶点u和v、起始时间戳t和终止时间戳t′,求在时间[t,t′]内,从顶点u出发到达顶点v最快的路径,即最晚时刻t从站A出发,最迟时刻t′到达站B,求所需时间最短的路径.
文献[26-27]也将EAP,LDP和SDP问题称为“Foremost Path”,“Reverse-Foremost Path”和“Fastest Path”问题.如图3所示是一个包含了6个顶点14条边的时序图,顶点表示车站,边表示车站与车站之间存在一条通路.其中边上的标签td,ta表示每条边的起始时间td和终止时间ta,3种不同带箭头的线表示3辆车b1,b2和b3的行驶路程.假设在时刻t=5在车站v5准备前往v1,即查询EAP问题,那么结果应为在时刻6搭乘b3从v5出发在时刻8到达v1;假设需要在时刻t′=13之前从车站v1到达v4,即查询LDP问题,那么结果应为在时刻10搭乘b1从v1出发,然后在v2换乘b2,最后乘坐b2在时刻13到达v4;假设在时刻t=5从车站v5出发,要在时刻t′=10之前到达v1,即查询SDP问题,那么结果应为在时刻6搭乘b3从v5出发在时刻8到达v1.

Fig.3 A temporal graph of traffic network图3 车辆交通网络的时序图
文献[26-27]提出了基于贪心算法的时序图上路径查询算法.这种算法以经典的Dijkstra算法为基础,通过枚举的方式求解EAP,LDP和SDP问题,该方法通过索引Lv来存储SDP的持续时间信息,Lv中包含了元素[sv,av],分别记录了路径P的起始时间和终止时间.以SDP问题为例,若要查找顶点u和v之间最短持续时间路径,首先初始化sv=t,av=t′,然后判断能到达顶点v的边是否能由顶点u到达,若能,则用较小的持续时间更新Lv,直到找到持续时间最小的路径为止.
因为基于贪心算法的路径查询思路比较简单,查询的效率也比较低,所以文献[26-27]提出了一种基于图转化的路径查询方法.这种图转换方法的基本思想是为时序图中的顶点构建副本,构成我们熟悉的静态图,然后在静态图上进行路径查找.将时序图转换为静态图后,通过广度优先遍历就可以直接解决时序图上的路径问题.由于将时序图转化为静态图后会增大原有的图规模,而且广度优先遍历的效率相对较低,所以该方法不能很好地适用于大规模图数据上.因此在文献[27]最后给出了时序图上并行处理路径问题的方法.
文献[25]提出了TTL(timetable labeling)算法为时序的边构建索引,来解决时序图上的路径问题.TTL算法为时序图G=(V,E)中的每个顶点构建TTL索引.TTL索引分为2个标签Lin(v)和Lout(v),每个标签是由一组标签l=x,td,ta,b,p组成的规范路径(canonical path),对于Lin(v),x为路径的起始顶点,v为路径的终止顶点,td为起始时间,ta为终止时间,b为搭乘的车辆(如果搭乘的车辆不是唯一的则为null),p为路径经过的编号最小的顶点(如果没有则为null);与Lin(v)不同的是,Lout(v)中v为路径的起始顶点,x为路径的终止顶点,而顶点u和v之间的规范路径P是指u和v之间即是最早到达又是最晚出发的路径.当给定查询顶点u和v、起始时间戳t和终止时间戳t′时,只需要从TTL表中找到可能的候选集,然后通过候选集找到符合要求的最短路径即可.该方法在生成的TTL表时需要消耗大量的时间和空间代价,虽然查询时间较短,但只适用于中等规模的图,在稠密图和大图中不能很好的应用.
2.2 时序图上可达性查询问题
可达性查询是用来回答在有向图中,一个顶点到另一顶点之间是否存在路径的问题.可达性查询作为最基本的图数据处理方法之一,在社交网络、生物信息网络和语义网中都扮演着重要角色,在多个计算机科学领域,如软件工程、社交网络、生物网络、编程语言、路由规划等都有很好的应用.在静态图中大量可达性索引方法被相继提出,这些方法大体可以分为2种:只依赖标签的方法[28-31];依赖标签和深度优先遍历的方法[32-34].只依赖标签来解决可达性查询问题,这类方法通常为图中顶点构建索引,以此来压缩传递闭包,然后通过顶点的标签关系来实现可达性查询.依赖标签和深度优先遍历的方法是指在可能的情况下,使用标签来解决可达性查询问题,对使用标签不能解决时或者代价太高的部分,用深度优先遍历来解决.但是由于时序图中顶点之间的边会受时间的影响,所以静态图上的可达性查询方法并不能直接移植到时序图上.
由于静态图上的可达性查询方法已经非常成熟,因此将时序图转化成静态图,然后通过静态图上的可达性查询方法来处理时序图上的可达性查询问题是最为简单的方法.文献[12]提出了TopChain方法来解决时序图上的可达路径查询问题.这种方法先通过为每个顶点构建副本,将时序图完全转成静态图,然后将图划分成不相交且包含了图中所有顶点的链,为每个顶点v构建标签(v.x,v.y),其中v.x是v所在链的编号,v.y是v在链中的位置.接下来根据链中顶点的关系为每个顶点构建Lin(v)和Lout(v)标签,Lout(v)中包含了k个链序号最小的且v能到达的顶点,同理Lin(v)中包含了k个链序号最小的且能到达v的顶点.当判断2个时序图中的原顶点u和v在时间阈值[t,t′]中是否可达时,只需要根据2个顶点在时间阈值中的副本{u1,u2,…,un}和{v1,v2,…,vm}上的标签之间的关系进行判断即可得到2个顶点间的可达信息.该方法的索引较为简单,但索引规模较大,只能应用于中小规模的图,在实际大图中不能很好的应用.
2.3 时序图上精确匹配问题
图上的精确匹配是目前应用最为广泛的图匹配技术,精确匹配问题是指给定数据图g和查询图q,判断g中是否有与q同构的子图.现有的在静态图上的子图同构方法可以分为2类:使用索引的方法[35-38]和不使用索引的方法[39-41].而在时序图中,若使用索引的方法来实现精确图匹配,则在构建索引时需要考虑时间的因素,这使得索引规模扩大.而在时序图中采用回溯的方法,由于时间会影响顶点之间的关系,所以很难得到查询图每个顶点的候选集.并且与静态图的精确匹配不同,时序图的精确匹配分为2种情况:
1) 时序图上的静态图匹配
时序图上的静态图匹配是指数据图为时序图,查询图为静态图.
2) 时序图上的时序图匹配
时序图上的时序图匹配是指数据图为时序图,查询图也为时序图.
对于时序图上的静态图匹配只需考虑数据图上的时间信息,然后参考静态图上精确匹配的方法,即可得到匹配结果.时序图上的时序图匹配问题则更为复杂,因为不仅需要考虑数据图上的时间信息,还需要考虑查询图上的时间信息,这使得构建查询候选集的工作更为复杂.如图4所示为时序图精确匹配的2种情况,其中图4(a)表示数据图,图4(b)表示时序图上的时序图匹配问题的查询图,图4(d)为图4(b)在图4(a)中的匹配结果,边上的标签标示这条边存在的时刻数据图中顶点D,C,B分别对应查询图中的a,b,c,其中边(D,C)出现在边(C,B)之前,且边(D,C)在时间阈值[7,9]内,边(C,B)在时间阈值[3,4]内.图4(c)为时序图上的静态图匹配问题的查询图,图4(e)为图4(c)在图4(a)中的匹配结果.
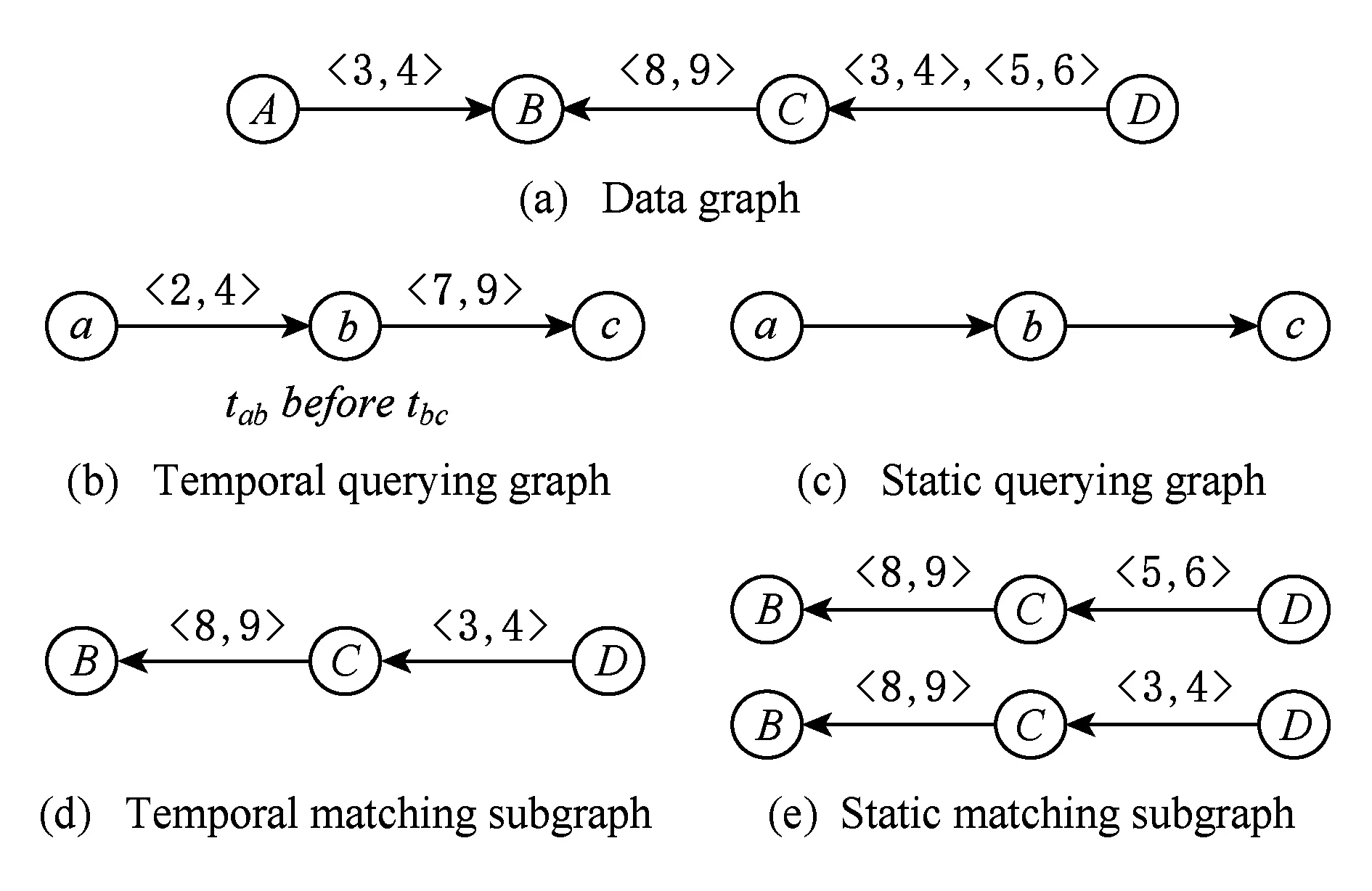
Fig.4 Querying temporal graph and static graph on temporal graph图4 时序图上的静态图匹配和时序图匹配问题
对于时序图上的静态图匹配问题,文献[2]根据在子图同构算法的不同阶段使用时间和拓扑信息提出了3种方法:Time before Topology (Ti-To),Topology before Time (To-Ti)和Time and Topology Together (Ti&To).Ti-To是先从数据图中提取所有与查询图时间相关的子图,然后应用子图同构算法找出满足条件的子图.其具体做法首先在数据图的边上使用广度优先算法搜索最大时序子图.在返回时序子图中依次检验是否满足子图同构的要求.实验证明该方法由于得到的子图可能具有很大程度的重叠,提取步骤非常耗时,因此效率不高.To-Ti是在整个数据图上进行子图同构,此时不关注时间信息,然后在返回的每个子图中检查时间信息,保留相符的结果.Ti&To是在进行子图同构的过程中考虑时间限制.同构过程由状态空间来描述,过程的每一个状态s描述了一个局部映射结果,在一个状态s中,首先判断由查询图的一部分与数据图的一部分组成的候选对是否是同构的,若同构,判断候选对的时间是否匹配,如果都匹配,则根据候选对中顶点的邻居顶点向下扩展成为新的候选对,根据上述步骤继续判断,直到找出所有满足条件的子图.Ti&To的效率要明显快于Ti-To和To-Ti,尤其当查询图路径较长时,Ti&To表现明显优于Ti-To和To-Ti方法.但是Ti&To只能用于时序图上的静态图匹配,实际应用有限.
对于时序图上的时序图匹配问题,文献[42]提出了2种用来解决时序图上的精确匹配的方法:TCGPM-V和TCGPM-E.TCGPM-V是一种基于顶点匹配的模式匹配方法,该方法首先使用深度优先搜索树找到所有顶点匹配集,然后依据这个匹配集来枚举出所有可能的时序子图,从中再找出正确的时序子图.与TCGPM-V不同的是,TCGPM-E是一种基于边匹配的模式匹配方法.该算法的主要思想是:首先依据该文提出的排序函数在模式图中选择一条计算结果最小的边;然后在模式图中计算以所选边为中心,其所能连接的最多边的数量r;再在数据图中找出所有与所选边匹配的边集,把数据图分解为边集中边的数量个子图,每一个子图中都含边集中的一条边并且子图中边的数量为r;最后在每一个子图上做子图同构匹配,枚举出匹配的时序子图.这2种方法虽然可以解决时序图上的时序图匹配问题,但是解决思路只是单纯地将时间作为一个限制条件,而忽略了时间之间的关联性.
2.4 社交网络上时序查询问题
随着社交网络用户的不断增多,社交信息的数量越来越庞大,根据用户和开发者需求进行搜索成为了社交网络必不可少的功能.在社交网络信息数据中,时间维度是最常见也是最重要的信息之一,例如当用户登录或注销账户时,后台数据库都会有一个时间戳来记录此类操作;当2个用户成为好友时,后台数据库也会有一个时间戳来记录这个事件;当用户发布一条状态、图片或者链接时,这类社交活动都被记录在时间戳上并保存下来.与传统查询只能反映出用户之间的关系不同,引入时间维度的社交网络时序查询可以区分出新与旧,活跃关系和不活跃关系等.包含时序信息的社交网络上的查询都是由一组基本查询构成的,基本的查询问题包括:
1) FIA查询
FIA查询是用来找出参与给定社交活动的好友.例如,用户想要在他的好友中找到在之前2个星期中发表了关于咖啡的微博.这个查询可以用来帮助用户通过时间找到感兴趣的事件或者人.
2) UTF查询
UTF查询是用来找到在一个时间阈值内活跃的用户,并且该用户的好友也参加了给定的兴趣活动.例如广告商希望找到在最近几个月都活跃的用户,并且该用户的好友已经参与了包含利益关系的活动,这样广告商就可以通过好友的影响说服用户购买他们的产品.
3) GURD查询
GURD查询是用来将用户按照给定数量分组,每组用户间的平均亲密度满足给定值,且所有的成员都参与了相同的活动.例如,餐馆为用户发放优惠券,目的是找到4人组(根据桌子大小),每组的亲密关系持续时间不少于一年,且4位成员都参加该餐馆的活动.
文献[43]在MVB树[44]的基础上提出了2种适应时序图的树形结构为时序社交网络构建索引:TUR树和TUA树.在MVB树中每个叶子顶点表示为key,ts,te,其中key是索引的值,[ts,te)是key的可用时间阈值.对于非叶子顶点key,ts,te,subnodeid,subnodeid表示子树的根顶点.因为MVB树只能用来表示用户,所以该文提出了TUR树用来表示用户关系.对于用户vi的key,用0|uidi表示,对于uidi和uidj之间的关系用1|uidi|uidj表示.当用户参与一个活动时,只需要用时间戳而不是时间阈值来表示时序信息,因此该文在B+树和Bloom Filter[90]的基础上提出了TUA树来为用户活动构建索引.对于TUA树,叶子顶点表示为key,ptr,其中ptr表示活动,key表示用户的ID和用户参与活动的时间,通过key来进行顶点的拆分,合并和重新分配操作.当内存溢出时,进行顶点的拆分操作,形成了一个新的根顶点来连接2个叶子顶点.然后该文通过由TUR树和TUA树构建搜索算法来计算3个基本查询.例如FIA查询首先用TUR树检查2个用户之间是否存在关系,然后通过TUA树判断用户是否参加了相应的活动.
3 时序图挖掘方法
数据挖掘,也称为知识发现(knowledge discovery from dataset,KDD)是用来抽取数据中隐含的、具有潜在用途的、人类可以理解的模式[45].长期以来,图数据挖掘问题得到了广泛的研究,并且在生物医学、社交网络分析等领域得到了广泛的应用,大量的图数据挖掘方法被相继提出.但是与静态图相比,时序图包含了时间信息,所以图的结构更为复杂,顶点和边包含的信息更多,这为时序图上的数据挖掘工作带来了巨大的挑战.
3.1 时序图上最小生成树问题
最小生成树问题是指为原图生成原图的极小连通子图,该连通子图包含原图的所有顶点,且连通子图的边数最小.最小生成树的应用十分广泛,许多复杂的查询都基于最小生成树问题,而且许多高效的图算法都是以构建最小生成树为基础的.所以解决最小生成树问题是进行时序图上查询处理与挖掘问题的基础.静态图上经典的最小生成树算法是Prim算法[46]和Kruskal算法[47],这2种方法都是基于贪心算法的,并且都能保证得到全局最优解.由于时序图引入了时间的因素,因此最小生成树问题由可以在多项式时间内解决的P问题变成了NP问题,而且其查询条件也与静态图上不同.如图5所示,时序图5(a)上的最小生成树分为2种情况:图5(b)MSTa和图5(c)MSTw:
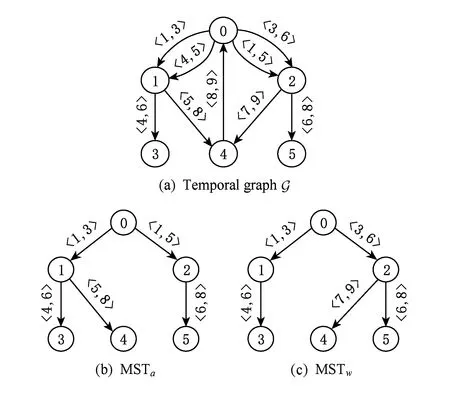
Fig.5 Temporal graph G and two types of minimum spanning tree图5 时序图及其2种形式的最小生成树
1) MSTa(具有最小持续时间的生成树)
MSTa是指对于一个生成树ST(r)=(VST,EST),根顶点r,当且仅当∀v∈VST,v≠r,在ST(r)中存在一条路径P使得r到v之间有最小的持续时间时,则称ST(r)是MSTa.
2) MSTw(具有最小权重的生成树)

文献[48]提出了解决时序图上最小生成树的方法.对于MSTa问题,该文作者首先把每条边按照起始时间的非递减顺序进行排序,然后输入根顶点和时间阈值,初始化顶点u的到达时间为无穷大,接下来对于序列中的所有边依次进行判断,如果该边的出发时间比上一顶点的到达时间大,或该边的到达时间比下一顶点的到达时间小,又或者该边的到达时间比规定的时间阈值的上限小,则将该边加入到生成树列表中,最后得到MSTa树.但是MSTa树要求每条边的持续时间不能为零,因此作者对该方法提出了改进.对于u的每一条出边按照出发时间的非递增顺序进行排列,然后对序列中的边进行判断,得到MSTa.对于MSTw问题,作者将其近似为最小斯坦纳树(steiner tree)问题,即找到指定集合中顶点连通且边权重总和最小的生成树.该方法为时序图构建顶点副本,将时序图完全转换成静态图,然后在静态图上构建最小斯坦纳树,从而解决时序图上的MSTw问题.
3.2 时序图上稠密子图挖掘问题
稠密子图是指图中内部边相对密集的子区域,即在这个区域中顶点与顶点间的关系相较其他部分更为紧密.稠密子图问题是图数据挖掘中一个重要的组成部分,是社区发现问题中基于密度聚类的分支,在社交网络分析、电子商务、生物学等领域应用广泛.此外一些图上的查询处理与挖掘问题,如图聚类、图压缩、可达查询等,都可以以稠密子图挖掘为基础进行研究.现有的许多研究工作都是关于稠密子图问题的[49-52],包括极大团、k-core、k-truss等.在时序图中,稠密子图会随着时间的不同而不同,而且即使在单一快照中增加或者减少一条边,找到其中的稠密子图已经是NP问题,而时序图是由一系列快照组成的,因此如何处理快照之间的联系是解决时序图上稠密子图问题的核心挑战.
在时序图上的稠密子图问题是挖掘在某个时间阈值上存在稠密子图,因此找到最可能存在稠密子图的时间阈值是首先要解决的问题.文献[53]中提出了一种挖掘稠密时序子图的方法.这种方法首先将时序图转换成一系列时间的快照,通过计算每张快照边上的权值,为时序图构建一个横坐标为时间戳的粘性密度曲线,该文证明了在粘性密度曲线的峰值附近最可能产生时序稠密子图.所以通过粘性密度曲线,可以得到时序图上最可能存在稠密子图的时间阈值.接下来,作者将稠密时序子图问题转换成网络价值最大化问题(net worth maximization optimization problem,NWM),通过解决NWM问题的思想,在最可能的区间内找到时序图上的稠密子图.该方法应用了时间快照的思路,将时序图分割成为一系列时间快照,这使得时序图上的时间序列被划分成为了时间片,而忽略了时间对图稠密性的影响.
文献[54]提出一种启发式稠密子图搜索策略.该方法先通过剪枝策略移除不存在于时序子图模式中的顶点和时间阈值,然后在新的时序图中,该文将该图划分成一系列快照,若这些快照是连续的,则按照一定顺序移除时序图中的顶点,然后判断剩余顶点是否仍能构成完整的时序图,若能则删除该顶点与该顶点相连的所有边;若时间快照是离散的,则根据离散的时间将新的时序图划分成多个子图,然后递归地查找这些子图,找到稠密子图.该方法在一定程度上保留了时序图上的时间关联性,但是完成该算法所需时间较长,在大图上不能很好地应用.
3.3 时序图上k-匿名问题
数据挖掘的目的在于从大量的数据中抽取有价值的信息,但是网络数据不仅保存了常规的浏览信息,还包含了许多敏感的私密信息,所以在数据的挖掘和使用的过程中保护个人隐私成为了研究者们考虑的一个重要问题.数据匿名是实现隐私保护的一个有效的手段,即通过隐匿和泛化技术,对数据中的部分信息进行处理,使他人无法从处理后的数据中推理出个人隐私信息.而k-匿名是隐私保护中最普遍使用的一种匿名技术.k-匿名技术最早是由文献[55]提出,该方法通过隐藏个人标识信息,使得每条记录至少与数据表中其他k-1条记录具有完全相同的标识符属性,发布精度较低的数据,从而减少被其他人推测出用户身份信息的概率.
文献[5]提出了一种在时序图上进行的k-匿名方法.该方法将时序图和多层网络相结合,将每个时间片段看作多层网络的一个层.该方法的流程如图6所示.给定一个时序图和期望的匿名k,首先该模型通过k-means衍生算法解决l1范式最小化问题从而得到一组时序度序列,该序列的每个顶点都是匿名的;然后检查输出的度序列是否是可实现的,即确保每个度序列都存在与之对应的时间片;最后通过匿名且可实现的度序列生成k-匿名时序图.该方法将时序图顶点分成了不小于k个组,每组中顶点拥有相同的时序度向量,并且确保了分组时尽量小的改变图的结构.该方法虽然解决了时序图上的k-匿名问题,但是该方法是基于时间片的,即只考虑当前时间的匿名保护,而忽略了时间对顶点关系的影响.
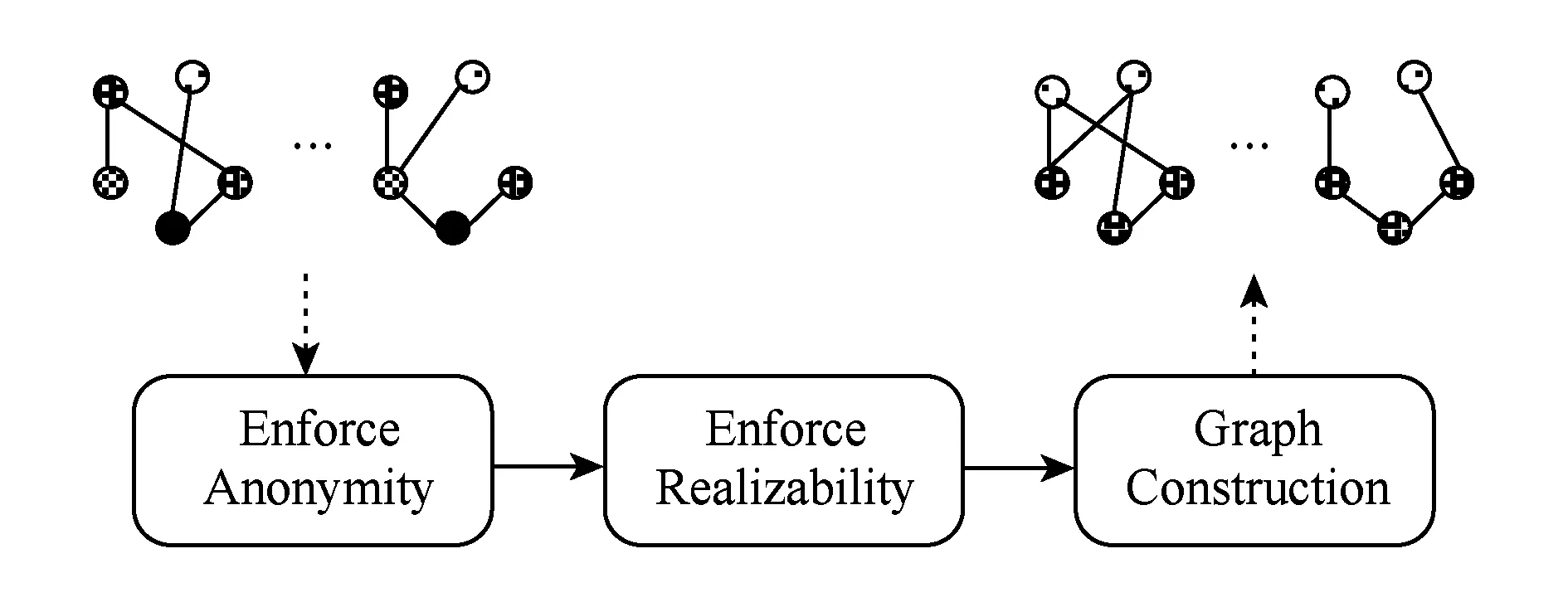
Fig.6 The framework of k-anonymity on temporal social graph图6 时序社交网络上的k-匿名方法框架
4 时序图数据管理系统
目前,已经有大量的图管理系统被提出,包括专门针对图数据的系统Neo4j[56],Titan[57],大型图处理框架包括Pregel[58],GraphLab[59],GraphX[60]等.但是这些数据管理系统都是基于静态图,即使有可以处理时序图数据的系统,也是基于演化的图数据库,即通过快照来对图数据进行管理,但是这些系统也只能保留最新的图快照,无法获得任意时刻上图的信息.

Fig.7 TGraph data flow architecture图7 TGraph数据流结构
文献[61]提出了时序图管理系统TGraph,该系统是由静态图管理系统Neo4j衍生出来,其中Neo4j是一个开源的图数据库,TGraph用Neo4j存储图中的顶点,关系和静态属性.而对于动态属性,如图7所示,TGraph先将数据写入内存数据结构MemTable中,然后将MemTable写入第0层的磁盘文件UnStableFile中,根据时间的改变依次递增地合并UnStableFile文件,直到第4层为止.然后将第4层的UnStableFile文件存放入StableFile中.每个UnStableFile和StableFile都保存了一个时间阈值内的数据,然后用MetaFile记录每个文件的名称和其存储数据对应的时间阈值.
TGraph将所有的变化都记录在内存中,随着时间的变化,数据的规模会不断变大,很多数据可能被重复记录,为了改善这种情况,文献[62]也在Neo4j基础上提出了一种利用多层索引结构实现的时序社交网络数据管理系统.该系统使用可穿戴的传感器收集随时间变化的社交网络数据,这些数据主要包括每对参与者之间建立联系的起始时间和终止时间,以此来获得随时间变化的接近性网络.顶点之间的边表示相应时间阈值内参与者之间的接近关系,系统利用Neo4j中的多层索引结构为接近性网络构建树形索引,每层树代表了不同时间尺度(如年、月、日等).该系统虽然通过多层索引结构提高了时序图的存储和管理效率,但是图规模越来越大,集中式的存储和管理已经不能满足人们的需求.
为了更好地存储和管理时序图,文献[63]提出了分布式时序图系统,可以根据制定的时间点检索到一个或多个历史快照.该文还提出了类树形的分布式分层索引结构DeltaGraph,通过索引记录时序图随时间变化的情况,并行地处理快照检索.DeltaGraph中叶子顶点是时序图中等距离选取的快照,边保存2个顶点之间的内容之差,当查询某一时刻的快照时,只需要找到该时刻的最小路径,合并路径上边的数据,即可获得所需快照.DeltaGraph通过分布式的方法提高了时序图的存储效率,但是将时序图划分成快照会忽略时间之间的关联,可能会损失部分信息,对进一步的数据管理带来不便.
5 总结与展望
时序图是目前最受关注的图结构之一,在多个领域中都有很好的应用,因此研究时序图上的查询处理与挖掘问题具有十分重要的理论意义和应用前景,引起了学术界和工业界越来越多的关注.由于引入了时间维度并且问题的定义与静态图和动态图不尽相同,时序图上的查询处理与挖掘问题不能完全依照已有的算法来解决,因此如何在现有的研究基础上,提出解决时序图上的查询处理与挖掘问题的方法,提高现有算法的效率是今后研究工作的一个新的探索方向.而且随着大数据时代的来到,数据规模不断扩大,数据结构越来越复杂,这给时序图上的查询处理与挖掘问题带来了更新更大的挑战,同时也给研究者们带了更大的机遇.
虽然时序图模型可以有效解决随时间变化网络中的问题,但并不是所有这类的问题都需要在时序图中解决.只有当一个网络有时序性结构,符合时序图的框架,并且涉及到时间标度时才需要用时序图来解决问题[64].而且如果动态系统的变换速度远快于动态连接的速度,或者图中的边是活跃变化的,那么就不需要将动态系统转换成时序图[2].例如网络中包的传输要比拓扑变化快得多,上述这种情况下就不需要在时序图上来解决包传输问题.总而言之,当一个系统有时序性并且拓扑连接遵循一定的动态变化,那么运用时序图框架来解决该系统上的问题将是一个非常高效的选择.下面本文根据当前工作的不足,给出未来可以研究的3个方面.
1) 提高时序图上查询处理与挖掘效率
虽然研究者们已经提出了一些时序图上的查询处理与挖掘方法,但这些方法的效率仍有很大的提升空间.例如在可达性查询问题上,时序图转换成静态图后会急剧扩大图的规模,如果能并行地处理可达性查询问题,将会大大提高查询的效率.对于k-匿名问题,现有的方法是基于时间片的,可是时序图中不同时间阈值内顶点之间的影响是不同的,所以如何创建基于时间阈值的k-匿名隐私保护方法具有很高的研究价值.现有的时序图上的查询处理与挖掘方法多是基于离散时间,这种时序图在现实应用中较为少见,更多的是连续时间上的时序图.因此如何扩展现有的时序图方法,使其不仅适用于离散的时序图还适用于连续的时序图,是未来研究工作需要关注的重点.
2) 提出更多时序图上查询处理与挖掘方法
虽然研究者们对时序图上的查询处理与挖掘问题已经有了初步的研究工作,但是很多在静态图上已经有了深入研究的经典问题在时序图上仍没有得到解决.如查询处理问题中的近似匹配问题、子图同态问题、关键字查询问题等.还比如挖掘问题中的SimRank问题、PageRank问题、影响力最大化问题、频繁子图挖掘问题等.这些问题在实际生活中都有很高的应用价值,如果能提出适用于时序图的方法来解决这些问题,将为图上后续研究工作提供良好的基础和技术支持.
3) 构建统一的时序图管理系统
现有的时序图管理系统都是在静态图管理系统的基础上单独保存时序信息,以此完成时序图的存储和管理.这种方法可能会重复保存或丢失部分时间信息,为时序图的管理带来不便,因此构建统一的时序图管理机制尤为重要.而且由于现有的图规模越来越大,集中式存储已经不能满足人们的需求,分布式存储成为了最为常见的存储方式.如果用分布式的方法来保存时序图,就涉及到了图分割问题.如何合理地对时序图进行分割,保证时序图的结构和时间信息完整是未来必须要解决的问题.
