基于负载电流前馈两级式单相逆变器输入电流低频纹波的抑制
2018-09-21黄永冰曹立波林丽燕黄其烟陶海欧
黄永冰,曹立波,林丽燕,黄其烟,陶海欧
基于负载电流前馈两级式单相逆变器输入电流低频纹波的抑制
黄永冰,曹立波,林丽燕,黄其烟,陶海欧
(福建和盛高科技产业有限公司,福建 福州 350001)
两级式单相逆变电路中,因输出功率的脉动,输入电流侧将出现大量纹波,且它的频率是输出频率的2倍。提出了一种基于前端DC-DC变换器负载电流前馈来减少输入电流低频纹波的控制策略,旨在控制母线电压以2倍的输出频率脉动,从而使直流母线电容提供几乎所有的脉动功率。阐述了实施方法,分析了动态特征、设计主要参数的原则。提出的前馈方法能有效地抑制输入电流纹波,而对原始系统的稳定性、动态响应等几乎没有影响。仿真结果证实了该控制方法的有效性和分析的正确性。
电流纹波;负载电流前馈;低频纹波;单相逆变器
两级式单相逆变器常常被广泛应用于各类配电系统中,比如不间断电源、光伏发电系统、船舶电力系统、燃料电池供电系统等场合中[1-5]。其由前级DC-DC变换器与后级DC-AC变换器组成。其中,前级变换器承担电气隔离与电压匹配的功能,而后级变换器负责将经过前级所得到的直流电转换成所需要的交流电。
对于单相逆变器,由于其瞬时输出功率会以2倍输出频率脉动,导致其输入的电流中存在二次谐波电流,这使得前级DC-DC变换器和输入源中产生2倍输出电压频率的脉动电流,也就是二次纹波电流[6]。同样,在两级式三相逆变器中,当三相负载不对称时,DC-DC变换器和输入源中也会产生二次纹波电流。
对于光伏发电系统,二次纹波电流将使光伏电池在最大功率点处发生功率振荡,这将影响最大功率跟踪的实现,进而降低系统效率[7]。对于燃料电池发电系统,二次纹波电流将增大燃料电池最大瞬时输出功率,这将使所需燃料电池的容量增大,导致系统成本增加。除此之外,当燃料电池中的二次纹波电流的峰值超过额定电流的8%时,燃料电池的效率会降低,它的使用寿命也会缩短。对于前级直流变换器而言,电流均值一定时,二次纹波电流将会导致电流有效值变大,进而增大开关管的电流应力和通态损耗。如果前级直流变换器采用软开关技术,二次纹波电流还会减小软开关的实现范围,使开关损耗增加,降低变换器的效率。
为了减小前级直流变换器和输入源中的二次纹波电流,可以选择增大中间母线电容的容量,但是这往往需要采用电解电容[9]。电解电容体积较大、寿命短,会降低系统功率密度和缩短平均无故障间隔时间。此外,增大中间母线电容并不能够完全消除前级直流变换器和输入源中的二次纹波电流[10]。在中间母线上并联1个双向变换器来提供单相逆变器所需要的脉动功率,能有效减小前级直流变换器和输入源中的二次纹波电流[11-14]。但这也会增加系统的成本以及控制系统的复杂性,并会降低系统可靠性。文献[10]在前级直流变换器引入电感电流内环并大幅降低电压外环截止频率,有效抑制了二次纹波电流,但是这一文献未明确阐述电压电流双闭环控制抑制二次纹波电流的机理。文献[15]通过反向电流传递增益对此进行了解释,但是该方法较为复杂、不直观。除此之外,较低的电压外环截止频率会导致系统动态特性变差,当负载跳变时中间母线电压会出现较大的跌落或过冲,中间母线电压较大的跌落将导致逆变器输出电压波形出现畸变,而较大的过冲将增大后级逆变器开关管的电压应力。
为了在不增加额外电路的情况下抑制低频输入电流纹波,本文提出了一种基于前端DC-DC变流器LCFF的控制策略。该策略通过修正直流母线电压参考值,同时,控制控制直流母线电压在2倍的特征频率下正常脉动,使得直流母线电容提供几乎所有的脉动功率。章节1给出了本文提出的控制策略的模型建立过程;章节2从输入电流中低频纹波抑制效果以及参数的敏感性分析方面对本文提出的方法进行了性能分析;章节3对两级式单相逆变器原型进行仿真验证,分析了其稳态与动态性能;本文的总结列写于章节4中。
1 模型设计
由于低系统具有的复杂性和成本,前级DC-DC换流器常使用电压控制模式来维持中间母线电压。BUCK变换的数字实现的传统控制策略如图1所示,为滤波电感,L为等效串联电阻,bus为直流母线电容,C为等效串联电阻,f和f分别是交流输出滤波电感和电容,load为负载阻抗。

图1 传统电压控制模型
v是电压控制器,传统的PI调节器通过比例环节设置合适的比例系数以消除偏差,再通过采用恰当的积分常数来消除静差,提高无差度,具体计算公式为:
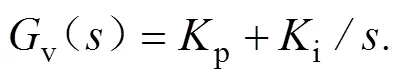

因此,延迟采样器与零阶保持器一起起到等效延迟作用,过程为:

图2为小型号模型下的buck型转换器,当带负载运行时,DC-DC转换器的直流负载含有大量的二次和高频谐波,iinv在A点将低频部分引入电压环,在电感电流和输入直流源中产生纹波。消除负载电流纹波最直接、最有效的方法是在电压环的A点增加赋值相同而方向相反的负载电流。通过将反馈节点从1/(SL+RL)的输出到输入环,即从A点到B点。等效的框图如图3所示。
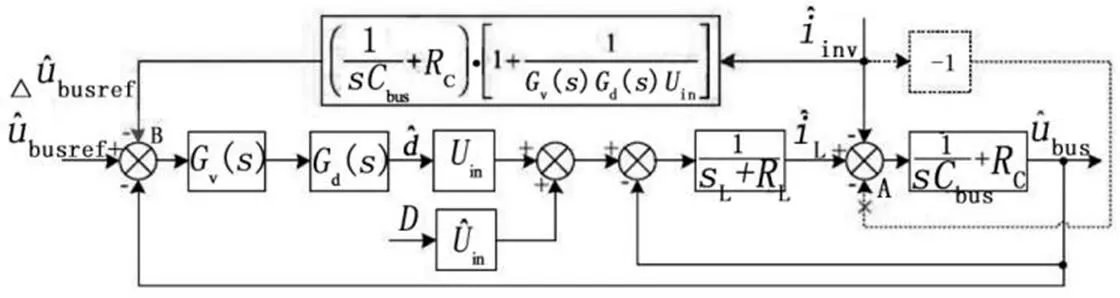
图3 引入反向负载电流后的小信号模型框图
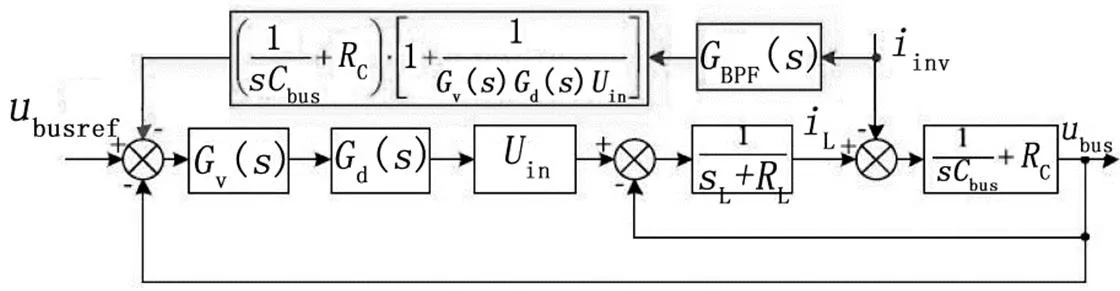
图4 大信号模型框图
我们仅考虑了在负载电流中的二次谐波部分,且带2o特性频率的带通滤波器被采用,用来抽取负载电流中的二次谐波。大信号模型如图4所示,带通滤波器的表达式为:
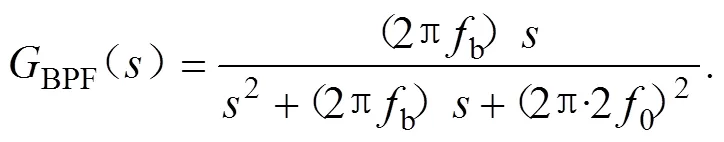
fb是BPF的带宽,取fb为20 Hz,伯德图如图5所示。
与传统的电压控制模式相比,1个额外的LCFF路径引入电压环,反馈节点在电压环的输入侧。这条路径给直流母线电压参考值轻微的调节。这证明电压参考值不是常量,最终参考电压为直流参考电压和纹波参考电压,LCFF传递函数为:
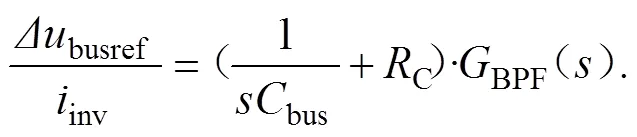

然而,控制表达式并不适用于实际应用,因此,提出了简化和修改方法,具体如下。
1.1 删除延迟函数Gd(s)
一方面,大多数电力系统中的采样和控制频率都远远高于2o,由延迟函数d()在2o处产生的滞后相位角非常小,延迟函数d()在2o处的相位角仅为3.4°,延迟函数d()对二次谐波成分的影响可以忽略不计;另一方面,尽管延迟函数d()将在高频时引起巨大的相位角变化,但是高频谐波成分在通过滤波器后会相当小。所以,式(5)中的d()可以直接删除,得到一个更容易实现的新的LCFF控制器,简化之后的传函如下:

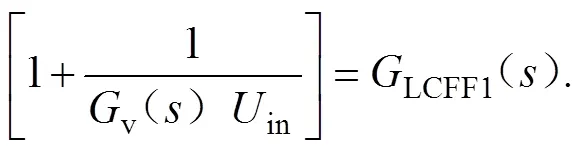
1.2 简化函数1+1/[Gv(s)Uin]
式(6)中函数1+1/[v()in]的频率特性完全由输入电压in和电压环控制器v()决定。当控制器参数确定并且输入直流电压大致保持常量,则可以确定其频率特性。此外,二次谐波是经带通滤波器滤波后被馈送到函数1+1/[v()in]的信号的主要成分,我们只关注频率特性为2o的部分。
为了获得足够的系统相位裕量,v()的截止频率L通常设计为不大于前端DC-DC转换器中LC滤波器的谐振频率res,截止频率L和谐振频率res各自定义如下:
L=i/(2πp). (7)

如果谐振频率fres低于2fo,则fL也小于2fo,实际上,许多两级单相系统中fres都不超过2fo,如图6所示。
当v()in的转角频率L比2o小时,在2o处及其附近处1+1/[v()in]的大小保持常数(在此表示为v)及其相位角接近0°。这表示函数1+1/[v()in]由于其频率特性可以由比例元件v代替,则式(6)可以简化为式(9),其中,v可以通过公式(10)计算:

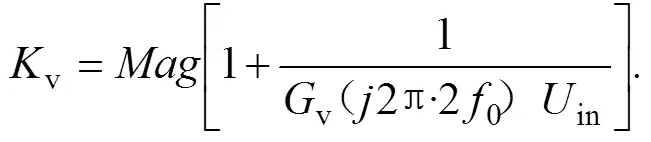
1.3 引入高通滤波器
在信号采样或负载阶跃变化的过程中,LCFF控制回路可能受到少量的直流或极低频干扰。通过1/(bus)元件的连续积分作用,导致中间直流总线电压出现较大的稳态跟踪误差。为了抑制直流偏置,在LCFF控制器的末端增加1个高通滤波器(HPF)。考虑到滑动平均滤波器(MAF)结构可以作为理想的低通滤波器,并在数字控制器中具有容易实现的优点,本文采用基于滑动平均滤波(MAF)的高通滤波器(HPF)。
滑动平均滤波基于统计规律,将连续的采样数据看成一个长度固定为的队列,每次采样到一个新数据,去掉原先队首的一次数据,其余-1个数据依次前移,新的采样数据放入队尾,并把队列中的个数据进行算术平均运算,获得新的滤波结果。
在域中表示的MAF的传递函数为式(11)[16],其中,s是滤波器在1个周期中采样的样本数。基于MAF的HPF的传递函数为式(12),滑动平均滤波器与高通滤波器的频率特性如图7所示。
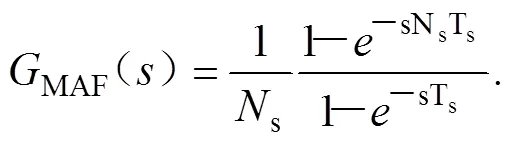
(12)
HPF具有接近36 Hz的截止频率,因此,它具有良好的抑制直流和非常低的低频分量能力,且不衰减2o处的分量。因此,LCFF控制器最终可以简化为:
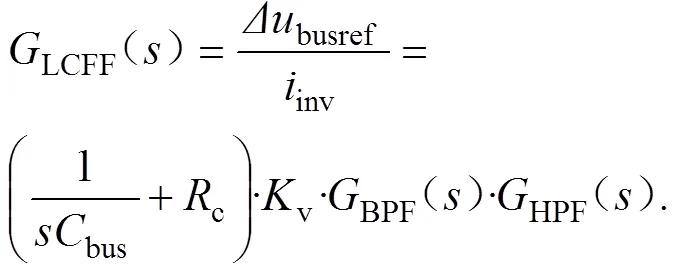
引入高通滤波器后的LCFF回路的结构如图8所示。
1.4 LCFF控制的实现
大多数系统可能没有DC-DC转换器负载电流传感器。在这种情况下,可以基于滤波电感电流L和直流母线电压bus,用式(14)计算负载电流的瞬时值,并将式(13)中的实际负载电流值inv替换为估计的inv,此外,为了避免差分分量,可以通过式(15)计算LCFF控制器输出,并且得到基于LCFF的低频输入电流纹波抑制的最终实现框图,如图9所示。

(15)
本文所提出的LCFF控制方法的实际意义可以概括为:由于我们希望中间直流总线电容器能够承担几乎所有的低频电流,这样将在直流总线上进一步产生相应的纹波电压,所以,对于瞬时直流母线电压的控制,设置参考值为常数是不合理的。本文所提出的方法可以通过引入新的路径,即向电压参考添加适当的纹波来解决问题。直流总线电压以2倍的输出频率脉动,可使直流总线电容器提供相应的低频纹波功率,从而防止纹波功率流入前级,这就使得输入了电流无纹波。因此,本文提出这种方法的控制策略与参考文献[17-20]中的控制策略有很大的不同。
2 性能分析
2.1 输入电流中低频纹波抑制效果
反向电流增益i()作为从输入电流in到负载电流inv的传递函数,其幅度可用于估计输入电流纹波减少的效果。
传统电压控制反向电流增益i0()与LCFF控制反向电流增益i1()如式(16)(17)所示:
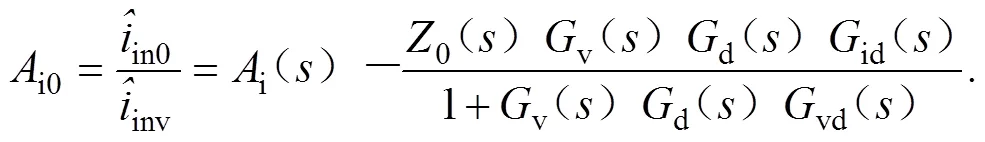

反向电流增益的幅频曲线如图10所示,对于没有LCFF控制的系统,2o处的反向电流增益i0()的幅度为-15.6 dB,没有达到衰减输入低频纹波的幅度。
随着LCFF路径的引入,反向电流增益i1()的幅度在2o处减小到-44 dB,并且在其他频率处保持不变。
2.2 参数的敏感性分析
图9中,bus和C分别是直流母线电容和等效串联电阻,从最终的LCFF控制框图中可以看出,电路元件参数bus和C在使用LCFF控制策略的时候的影响是必须要了解的。因此,分析这些参数对LCFF的影响是必须的。
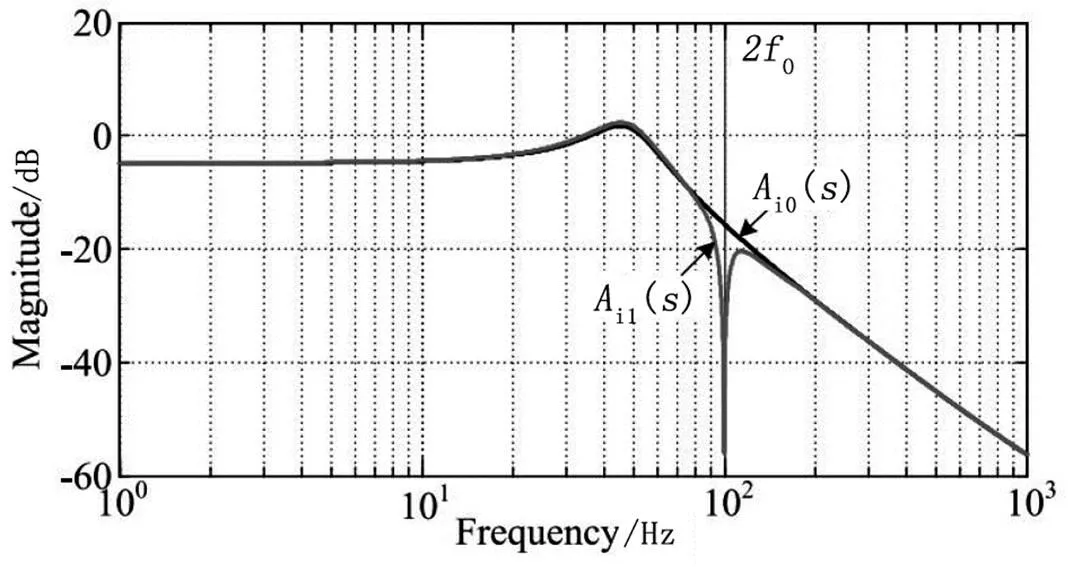
图10 反向电流增益的幅频曲线
参数C对LCFF影响可以忽略,原因如下。
电容的等效电阻值可以通过并联多个电容来减小。电解电容经常用来做母线电容,电容值与等效电阻值为常量,电解电容值一般范围为8.0×10-5~5.0×10-5.在式(15)和(17)中,C的出现形式为1+sbusC,sbusC值远小于1,可以忽略它的影响,将1+sbusC等效为1,就像C在等式中可以忽略,所以,其对LCFF性能影响很小。所以,C的值是否精确对LCFF控制器的设计并不重要。
参数bus的精确性对LCFF性能有一定影响,这个影响可以接受。
定义bus在实际电路中为直流母线电容,bus-ctrl是用在LCFF控制器中的直流母线电容,在一些情况下,bus-ctrl不等于bus.考虑到电容误差在±20%,则bus-ctrl/bus波动范围为0.8~1.2.
在2o处反馈电流增益幅值与电容误差关系曲线如图11所示。

图11 2fo处反馈电流增益幅值与电容误差关系曲线
电容误差为0时,在没有使用LCFF时纹波电流含量为29.1%;采用LCFF后为29.1%,文献[21]说明,纹波电流百分数应小于10%,完全可以达到要求。
因此,控制器中使用的电容的精度确实对LCFF性能有影响,但是即使电容误差达到-20%,具有LCFF的系统仍然具有良好的消除波纹性能。此外,±20%电容误差非常大,实际情况将会比这好很多。总之,LCFF控制对参数精度有一定的依赖性。然而,在大多数应用中控制性能是可接受的。bus和C的参数可以直接从数据表中获取,在此情况下参数准确度影响不大。如果需要具有更好的纹波抑制性能,也可以使用精密LCR仪表。
3 仿真验证
为了验证所提出的方法的性能,在图12所示的两级单相逆变器上测试没有LCFF控制和具有LCFF控制的VMC的运行性能。
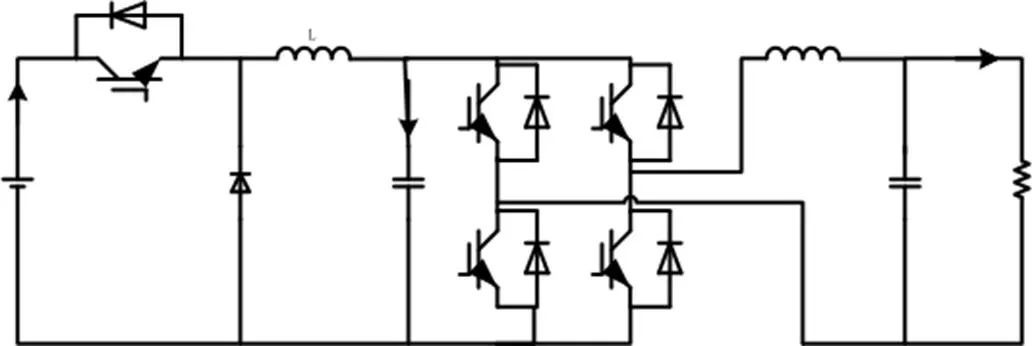
图12 两级式单相逆变器主电路
3.1 稳态性能分析
3.1.1 在2.5 kW时稳态电路波形
图13与图14分别为2.5 kW下在没有LCFF和具有LCFF时的系统中的稳态实验波形。在2.5 kW下bus的关键谐波分量比较如表1所示,在2.5 kW下in的关键谐波分量比较如表2所示。

图13 2.5 kW下且没有LCFF时的稳态电路波形

图14 2.5 kW下且伴随LCFF时的稳态电路波形
3.1.2 在5 kW时的稳态电路波形
图15与图16分别为2.5kW下在没有LCFF和具有LCFF的系统中的稳态实验波形。在5 kW时bus的关键谐波分量比较如表3所示,在5 kW时in的关键谐波分量比较如表4所示。
表1 在2.5 kW下的关键谐波分量比较
有无LCFFDC分量二次谐波/(%) 没有LCFF实验结果400.00.54 理论结果400.00.83 伴随LCFF实验结果399.00.47 理论结果400.00.64
表2 在2.5 kW下的关键谐波分量比较
有无LCFFDC分量二次谐波/(%) 没有LCFF实验结果4.0726.21 理论结果3.6129.14 伴随LCFF实验结果3.993.01 理论结果3.611.05
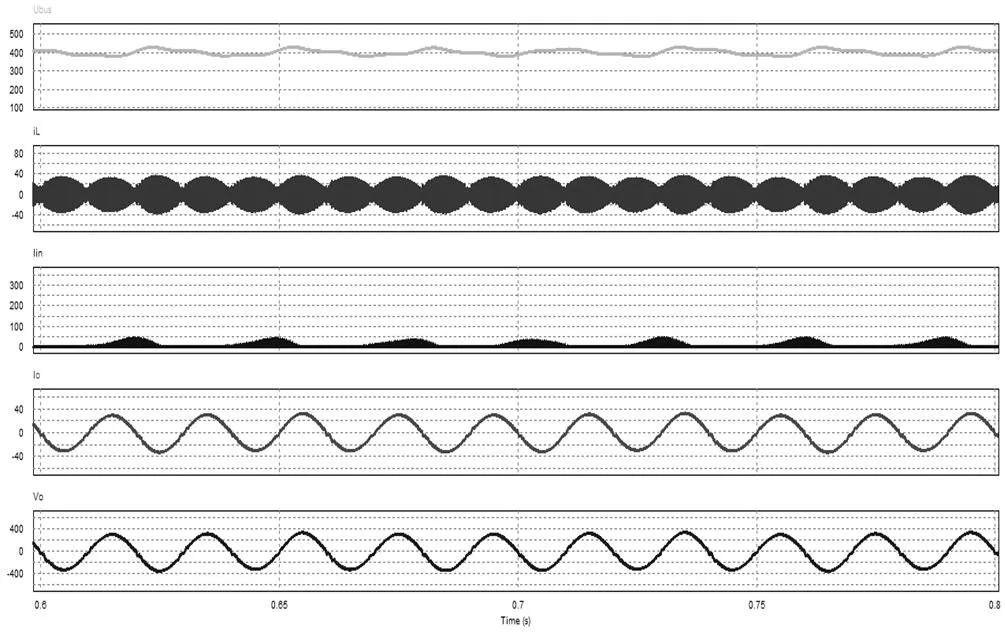
图15 5 kW下且没有LCFF时的稳态电路波形

图16 2.5 kW下且伴随LCFF时的稳态电路波形
表3 在5 kW时的关键谐波分量比较
有无LCFFDC分量二次谐波/(%) 没有LCFF实验结果399.71.31 理论结果400.01.53 伴随LCFF实验结果399.61.18 理论结果400.01.22
表4 在5 kW时的关键谐波分量比较
有无LCFFDC分量二次谐波/(%) 没有LCFF实验结果7.6620.1 理论结果7.1425.09 伴随LCFF实验结果13.51.85 理论结果7.140.65
3.2 动态性能分析
图17与图18分别为没有和具有LCFF控制的系统的瞬态响应,其中ac输出负载从2.5 kW变化到0.4 kW,然后再回到2.5 kW。VMC控制与LCFF控制策略的动态性能的比较如表5所示。
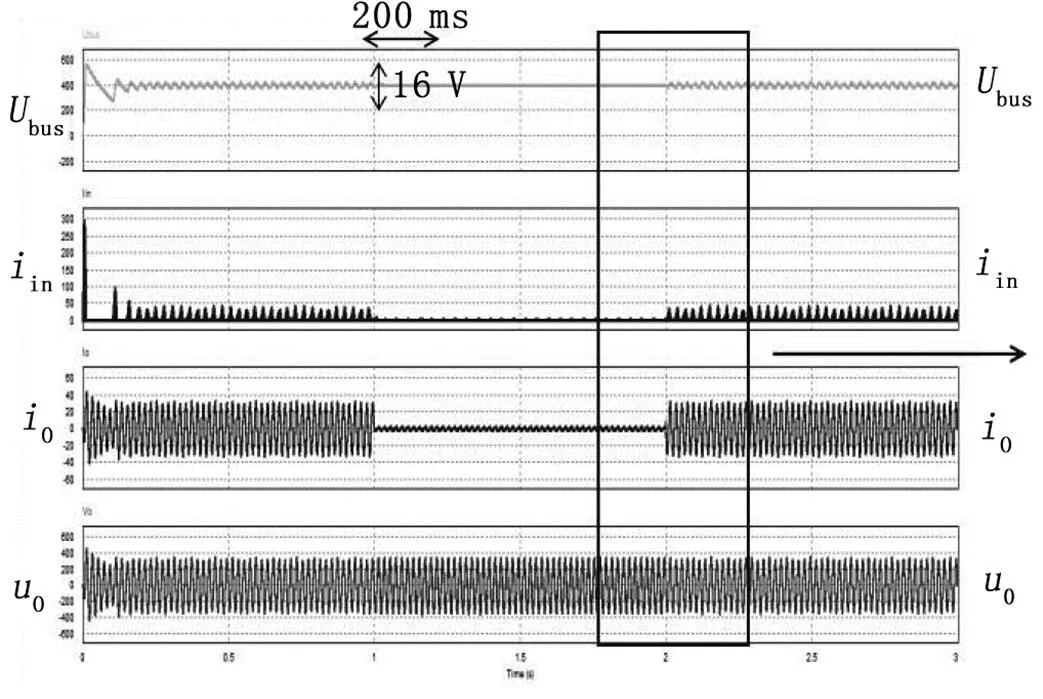

表5 VMC控制与LCFF控制策略的动态性能的比较
有无LCFF负载2.5 kW至0.4 kW负载0.4 kW至2.5 kW 没有LCFF200 s100 s 16 V12 V 伴随LCFF280 ms100 ms 15 V12 V
4 结论
为了解决两级单相逆变器中由脉动功率引起的输入电流低频纹波问题,本文提出了基于前端DC-DC变换器LCFF的一种控制方法。它旨在控制中间直流母线电压在输出频率2倍时处于正确摆动,并使得直流总线电容提供几乎所有的纹波电流。通过仿真验证了该方法的可行性与有效性。本文所提出的LCFF控制策略的主要特性可以归纳为:①输入电流纹波得到很好的抑制,对原始系统的影响很小;②电流纹波抑制的实现不需要额外的电路。
此外,因为该方法并不是基于降压转换器特有的任何特征,所以,利用LCFF来减小输入电流纹波的想法可以进一步扩展到其他类型的降压(也称为电压源型)DC-DC转换器,例如推挽前馈、移相全桥等。
[1]Xue Y,Cahng L,Kjær S B,et al.Topologies of single-phase inverters for small distributed power generators:an overview[J].IEEE Transactions on Power Electronics,2004,19(05):1305-1314.
[2]Kjær S B,Pedersen J K,Blaabjerg F.A review of single-phase grid-connected inverters for photovoltaic modules[J].IEEE Transactions on Industry Applications,2005,41(05):1305-1314.
[3]Tao H,Duarte J L,Hendrix M A M.Line-interactive UPS using a fuel cell as the primary source[J].IEEE Transactions on Power Electronics,2008,55(08):3012-3021.
[4]Kwon B H,Choi J H,Kim T W.Improved single-phase line-interactive UPS[J].IEEE Transactions on Industrial Electronics,2001,48(04):804-811.
[5]Kwon J M,Kim E H,Kwon B H,et al.High-efficiency fuel cell power conditioning system with input current ripple reduction[J].IEEE Transactions on Industrial Electronics,2009,56(03):826-834.
[6]Jung S,Bae Y,Choi S,et al.A low cost utility interactive inverter for residential fuel cell generation[J].IEEE Transactions on Power Electronics,2007,22(06):2293-2298.
[7]M A Vitorino,M B R Correa.Compensation of DC link oscillation in single-phase VSI and CSI converters for photovoltaic grid connection[C]//Proceedings of IEEE Energy Conversion Congress and Exposition.Phonix, USA:IEEE,2011:2007-2014.
[8]Fontes G,Turpin C,Astier S A,et al.Interactions between fuel cells and power converters:Influence of current harmonics on a fuel cell stack[J].IEEE Transactions on Power Electronics,2007,22(02):670-678.
[9]Itoh J,Hayashi F.Ripple current reduction of a fuel cell for a single-phase isolated converter using a DC active filter with a center tap[J].IEEE Transactions on Power Electronics,2010,25(03):550-556.
[10]Liu C,Lai J S.Low frequency current ripple reduction technique with active control in a fuel cell power system with inverter load[J].IEEE Transactions on Power Electronics,2007,22(04):1429-1436.
[11]Palma L.An active power filter for low frequency ripple current reduction in fuel cell applications[C]//Proceedings of IEEE Power Electronics Electrical Drives Automation and Motion.Pisa,Italy:IEEE,2010:1308-13139.
[12]李红波,张凯,赵晖.高功率密度单相变换器的直流有源滤波器研究[J].中国电机工程学报,2012,32(15): 40-47.
[13]Wang R,Wang F,Boroyevich D,et al.A high power density single-phase PWM rectifier with active ripple energy storage[J].IEEE Transactions on Power Electronics,2011,26(05):1430-1442.
[14]Krein P T,Balog R S.Cost-effective hundred-year life for single phase inverters and rectifiers in solar and LED lighting applications based on minimum capacitance requirements and a ripple power port[C]//Proceedings of IEEE Applied Power Electronics and Exposition Conference.Washington DC,USA:IEEE,2009:620-625.
[15]王建华,卢旭倩,张方华,等.两级式单相逆变器输入电流低频纹波分析及抑制[J].中国电机工程学报,2012, 32(06):10-16.
[16]J.I.Y.Ota,Y.Shibano,N.Niimura,et al.“Aphase-shifted-PWM D-STATCOM using a modular multilevel cascade converter(SSBC)Part I:Modeling,analysis,and design of current control”[J].IEEE Trans.Ind.Appl,2015,51(01):279-288.
[17]J.Wang,B.Ji,X. Lu,et al.“Steady-State and dynamic input current low-frequency ripple evaluation and reduction in two-stage single-phase inverters with back current gain model”[J].IEEE Trans. Power Electron,2014,29(08):4247-4260.
[18]L.Zhang,X. Ren,X.Ruan.“A bandpass filter incorporated into the inductor current feedback path for improving dynamic performance of the front-end DC-DC converter in two-stage inverter”[J].IEEE Trans. Ind. Electron,2014,61(05):2316-2325.
[19]G. Zhu,X. Ruan,L. Zhang,et al.“On the reduction of second harmonic current and improvement of dynamic response for twostage single-phase inverter”[J].IEEE Trans. Power Electron,2015,30(02):1028-1041,Feb,2015.
[20]L. Zhang, X. Ruan, and X. Ren.“Second-harmonic current reduction and dynamic performance improvement in the two-stage inverters:An output impedance perspective”[J].IEEE Trans.Ind.Electron,2015,62(01):394-404.
[21]C. Liu and J. S. Lai.“Low frequency current ripple reduction technique with active control in a fuel cell power system with inverter load”[J].IEEE Trans. Power Electron,2007,22(04):1429-1436.
2095-6835(2018)18-0039-07
TM464
A
10.15913/j.cnki.kjycx.2018.18.039
〔编辑:张思楠〕
