基于数字图像的自适应多机动目标模型跟踪方法
2018-09-20刘钢王蓉晖
刘钢,王蓉晖
(1.空军航空大学基础部,吉林长春,130022;2.吉林建筑大学电气与计算机学院,吉林长春,130018)
1 几种典型的机动目标模型
1.1 辛格模型

1.2 当前状态统计模型

其中a(t)为机动加速度当前均值,在每一采样周期内为常数。
把上式带入一阶时间相关方程,可得:

将上式写为状态方程,即为机动目标“当前”统计模型:

1.3 阶跃模型


W(k)和 V (k)是不相关的高斯白噪声序列。F (k)为状态转移矩阵,表达式为:

2 Monte Carlo仿真实验
在常加速度情况下,比较辛格模型和当前状态统计模型,进行目标加速度估计。这里α=0.1,T=1s,a = 2 0 m /s2,时间是在 t = 0 ~100s,图1中实线和离散点分别描绘的是当前状态统计模型和辛格模型的加速度统计。辛格模型的均方根误差为2.83,均值误差为0.59;当前状态统计模型的均方根误差为1.95,均值误差为-0.14。
如图2所示,变加速机动不适合辛格模型。所以在这里比较了当前状态统计模型和阶跃模型。图2是在变加速度情况下,进行目标加速度估计。如图2中离散点描绘的是阶跃模型的加速度统计,实线描绘的是当前状态统计模型的加速度统计。阶跃模型的均方根误差为3.64,均值误差为0.92,当前状态统计模型的均方根误差为2.86,均值误差为-0.34。
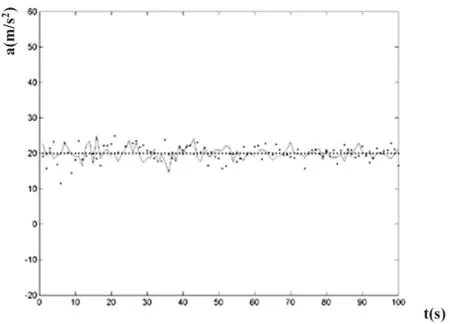
图1 常加速运动的目标加速度估计

图2 变加速运动的目标加速度估计
下面比较了当前状态统计模型和阶跃模型。这里α=0.1,T= 1 s,如图3中离散点描绘的是当前状态统计模型的加速度统计,实线描绘的是阶跃模型的加速度统计。阶跃模型的均方根误差为4.78,均值误差为1.65;当前状态统计模型的均方根误差为6.23,均值误差为-1.82。
通过目标的机动辨识,分辨出目标属于匀速运动、匀加速度、变加速度等不同情况,来自适应地选择不同适合的模型进行目标跟踪,通过仿真试验,采用该方法在匀加速转为加速度阶跃机动情况下,均方根误差为3.92,小于仅采用当前统计模型或阶跃模型的均方根误差6.23和4.78,跟踪精度得到改善。
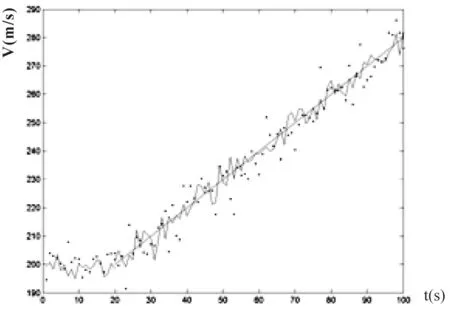
图3 阶跃加速度目标的速度估计
3 结论
因为不同的机动目标模型对于不同的机动特性的目标表现出了各自的优越性,但何时采用何种机动目标模型进行机动预测与估算,发挥出各自模型的优势,这是本文提出的主要论点,通过机动目标前几次的检测和速度、加速度目标测算,进行机动辨识,分辨出机动类别,通过选择模型进行目标机动预测和类型判别达到目标跟踪的目的,通过实验表明通过此种方法的计算,跟踪精度得到了较大提高。
