基于直觉模糊集下的工程评标研究

董明娟

（广东天联电力设计有限公司，广东广州，510663）

1 定义

1.1 模糊集

定义2.1[1]设X是一个非空集，则X上的模糊集A定，其中，µA(x)∈ [0,1]，称µA为x的隶属度，1-µA为x的非隶属度，函数µA( x)为x的隶属函数。为了方便起见，模糊集简记为{µA}。

在实际决策问题中，由于客观事物的复杂性、信息的不确定性及决策者思维的模糊性，采用模糊集往往不能很好地反映决策者的主观意愿和决策意见。为此，保加利亚学者Atanassov将模糊集进行了拓展和推广，于1986年提出了直觉模糊集，它增加了一个新的属性参数—犹豫度，更加完整地刻画了客观世界的模糊性本质，比传统的模糊集更具灵活性和实用性[1]。

定义2.2[1]设X是一个非空集，则X上的直觉模糊集和分别为X上元素x∈A的隶属度和非隶属度，且满足。为了方便起见，直觉模糊集简记为。

1.2 多属性决策方法

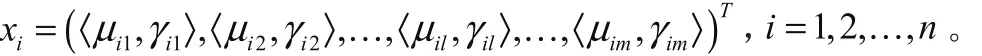
1.3 直觉模糊c均值聚类算法

模糊c均值聚类算法主要是通过优化基于某种范数和聚类原形的目标函数得到每个待分类对象对所有聚类中心的隶属度，从而决定分类对象的类属以达到自动进行分类的目的[2]。

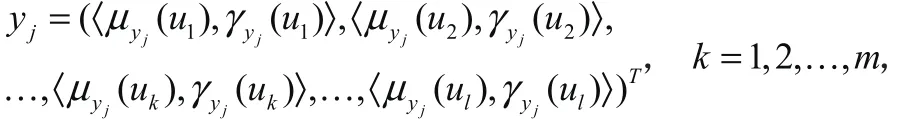
那么分类对象集合可表示成一个n×l的矩阵，即：Y =(〈 µjk, γjk〉 )n×l。相应地，每一个聚类中心 vi可表示为 ：

V =(〈 µki, γki〉 )l×c。因此，分类对象 xj与聚类中心 vj之间的模糊分类矩阵可表示为：P = ( µij)c×n。由模糊c均值聚类算法可知，直觉模糊c均值聚类算法的目标函数为：

其中，m＞1是模糊系数，一般取2；µij是第j个分类对象 yj属于第i类的隶属度值；dij( yj, vi) 表示从样本点yj到中心 vi的距离，本文采用直觉模糊集的欧式距离，即个关于自变量(,)PV 约束优化问题，可采用Lagrange乘子法来求解上述的数学规划问题，利用极值点的KT必要条件可以得到如下的迭代方程：

1.4 直觉模糊c均值(IFCM)聚类算法的应用

直觉模糊c均值聚类算法的应用需要事先确定最佳聚类数c。因此，首先通过Matlab编程得到模糊聚类有效性指标目标函数的最值，然后采用直觉模糊c均值聚类算法对数据集合进行分析，具体做法如下：

步骤1初始化直觉模糊c均值聚类算法的目标函数中的相关参数，令 m = 2 ，c(1 ＜ c＜n)，收敛精度ε＞0，Matlab程序会随机产生并归一化模糊划分矩阵 P(1)，令迭代次数 k = 1，且 k ≥ 1 ；

2 案例分析

表1 x1的专家打分表

表2 x2的专家打分表

2.1 传统模型

对专家评分汇总求和即得到投标文件的综合评分表，见表3。

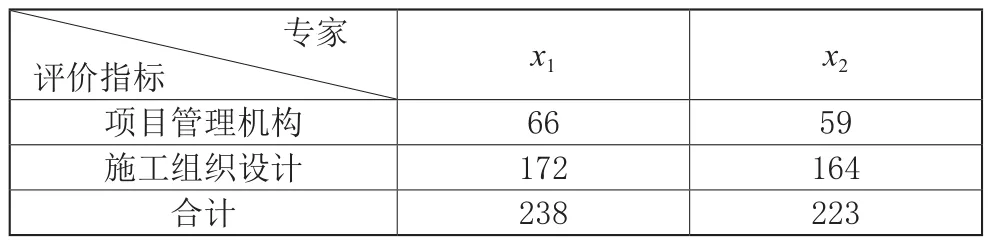
表3 综合评分表

从综合评分表可以得出，投标人1为第一中标候选人。

2.2 聚类中心模型

步骤1依据定义2.2可将专家评分值转化为直觉模糊集，见表4/表5。

表4 x1的专家打分表

表5 x2的专家打分表

步骤2利用Matlab编程，令收敛条件为：ε = 1 0-8，得到投标文件 x1的最佳聚类数是3，投标文件 x2的最佳聚类数为2，分类结果如下所示：

步骤4由直觉模糊c均值聚类算法得到聚类中心为：

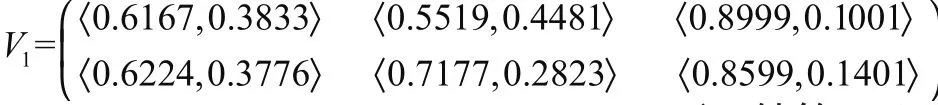
步骤5利用定义2.3的先对聚类中心进行聚合，再对属性聚合，得到投标文件的综合评分值。

由模糊集的定义可知，隶属度越大方案越优，因此，投标文件2为第一中标候选人。

2.3 案例分析

从专家打分表可以看出，专家1相对于其他专家对投标文件的打分有失公平，对投标文件1的打分相对较高，得到的评标结果可能不准确，而聚类中心模型对专家打分进行了分析，决策结果与实际情况相符。本算例验证了其可行性和有效性。