基于递归VMD的有源滤波器谐波检测

王金玉， 张建波， 何明敏

(1.东北石油大学，黑龙江 大庆 163000;2.中国石油天然气股份有限公司管道郑州输油气分公司，河南 郑州 450003)

0 引 言

自改革开放以来，我国工业发展迅猛，电力电子技术的广泛应用，使电力系统遭受严重的谐波污染。电网谐波是降低电能质量的主导因素，对电网的危害主要表现在：破坏系统稳定运行；影响电气设备的正常运行；高次谐波电路的电感值增加，引起共振进一步放大谐波电流；缩短用电设备的寿命。

谐波检测是处理谐波问题的前提，也是有源电力滤波器技术的关键技术之一[1]。谐波检测技术的发展直接决定着有源电力滤波器技术的发展。国内外学者最早提出的是模拟滤波，傅里叶变换在快速傅里叶变换出现后得到极大地关注。但是这些方法自适应不高，精度不够。随着现代信号处理理论研究的深入，学者们将瞬时无功功率引入到有源滤波谐波检测中，但是理想低通滤波器的实现很困难。文献[2]所提出的基于EMD的EEMD谐波检测方法对于检测特定次数谐波分量难以实现自适应检测。

针对目前谐波检测方法所面临的问题，在比较常见谐波检测方法必要前提条件的基础上，结合递归VMD理论，改进有源滤波器中谐波电流检测技术。对递归VMD应用于分离高次谐波以及基波重构进行了研究，并通过仿真试验，与经验模态分解(Empirical Mode Decomposition，EMD)方法对比来验证基于递归VMD的有源滤波器谐波检测的有效性。

1 VMD方法

1.1 VMD理论

VMD方法是Konstantin Dragomiretskiy于2014年提出的一种新的可变尺度的信号处理方法[3]。VMD的目的是将输入信号分解成离散数量的子信号(模态)uk，重构原信号。为了获得模态带宽，提出了以下方案：

(1)解析信号在理论分析上有很多优点。实际信号一般都是实信号，VMD理论利用希尔伯特变换把实信号变换为解析信号，用来获得每个模态uk的单边频谱。

设有实信号x(t)，其希尔伯特变换定义为：

(1)

也可以表示为：

(2)

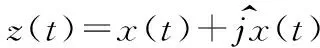
(2)通过频率混合，把每个模态函数uk的频谱移到基带。最简单的频率混合是乘法，通过乘法将两个频率不同的信号混合在一起，实现频率位移的效果。通过模态函数uk与估计的每个模态函数的中心频率ωk混合的方式，来把模态函数uk的频谱移到基带。

(3)通过解调信号的高斯平滑度来估计带宽，产生的约束变分问题如下：

(3)

式中:{uk}表示各模态函数的集合；{ωk}表示各中心频率的集合；δ(t)为单位冲击函数；f表示原信号。

VMD引入了二次惩罚项和拉格朗日乘子法。有限权重的二次惩罚项具有良好的收敛性，拉格朗日乘数具有严格强制约束，两种方法相结合使有约束问题转化为无约束问题。同时应用交替方向乘子法(ADMM)求解式(3)原始最小化问题。

(4)

步骤如下：

(1)求泛函的uk极小值

(5)

(2)求泛函ωk的极小值

(6)

(3)迭代约束条件：

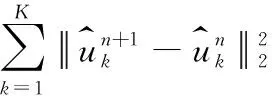
(7)

1.2 端点处理

端点效应影响VMD分解的质量。VMD在处理信号时，需要估计其窄带，这就使信号窄带边界上常常会出现失真现象，这通常称为边界效应[4]。在VMD分解中，信号两端的边界效应所带来的误差会使分解结果严重失真。目前针对端点抑制效应的方法有镜像延拓法、平行延拓法、极值延拓法和多项式拟合延拓法。本文针对VMD分解信号的特点，采用镜像闭合延拓法。

2 递归VMD

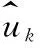
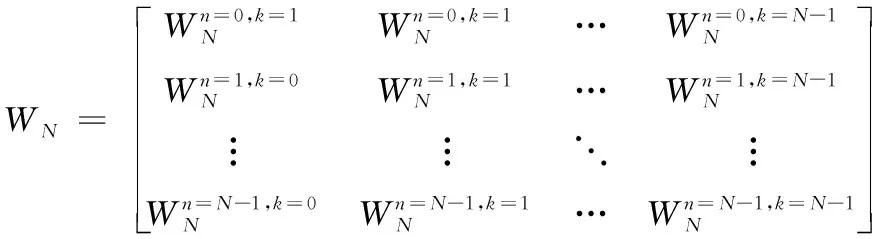
(8)

下一个瞬时处理块xnext=[x(1)x(2)…x(N-1)x(N)]。xnext可以看成序列x1=[x(N-1)x(1)…x(0)]和序列x2=[00…x(N)-x(0)]的和。其中x1是原信号被样本1移位的结果，x2是序列xinitial与序列xnext的和。通过傅立叶变换的线性特性可得，xnext的变换系数是x1和x2的对应系数的差。x1的变换系数由傅里叶变换的移位属性给出，x2的系数通过将x(N)-x(0)乘以WN的最后一列求得。因此在每个阶段，当前块的傅里叶变换可以计算为：

(9)

Xnext(k)=[Xinitial(k)+x(N)-x(0)]ej2πk/N

(10)

3 仿真与试验结果分析

为了验证VMD谐波检测的效果基于文献[6]待处理信号，对其进行分析。并将递归VMD谐波检测结果与EMD方法检测结果进行比较。输入信号的原始波形MATLAB仿真结果如图1所示,图2～图6为经VMD分解之后的重构模态图形。

图1 原始输入信号波形MATLAB

图2 重构模态1

图3 重构模态2

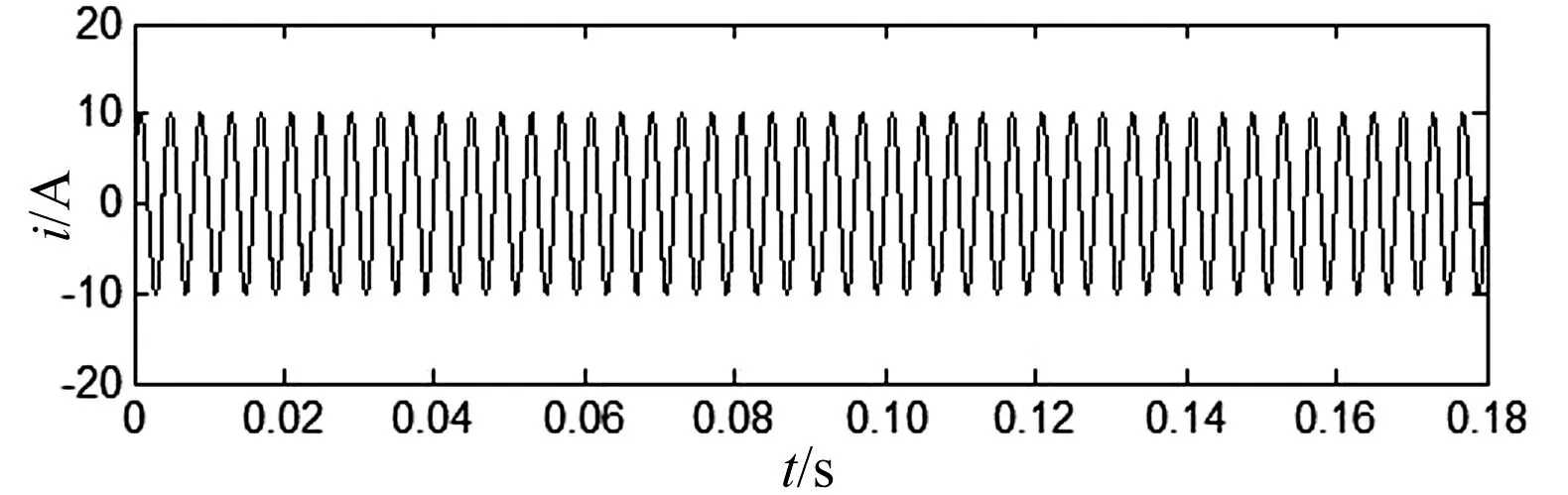
图4 重构模态3

图5 重构模态4

图6 重构模态5

由于递归VMD中每个BIMF分量的中心频率和带宽不断地相互交替迭代更新，最后自适应地分解信号的频带，模态函数uk频率由低到高排列，第一个重构模态为基波，其余依次为三次，五次，七次，九次谐波。在图2中，虚线表示输入信号原始谐波分量波形图，实线表示经过递归VMD分解之后的基波以及各次谐波分量。从图2可以看出，递归VMD方法准确检测出了基波分量，同时近乎完美地重构了各次谐波分量。为了检验递归VMD算法对于有源滤波器谐波检测的效果，将原信号中谐波分量作为参考，计算VMD算法所提取的谐波分量和原信号的谐波分量相关度。调用MATLAB中相关度计算函数R=corrcoef()，计算结果为：

此时的计算结果为0.999 5，说明递归VMD算法提取的谐波分量和原信号谐波分量的相关度非常高。

图7是基于EMD的谐波检测波形图。由于EMD是根据信号局部特征从小尺度到大尺度逐次将信号分为不同时间尺度的IMF分量，但是电网中的高频噪声分量将被分解到高阶IMF中。这就造成了模态混叠现象。所以，图7中的IMF1可以看成高频噪声，但是其余IMF分量不能准确找出各次谐波的波形，出现了模态混叠现象。同时EMD方法对基波分量的提取也有较大误差。

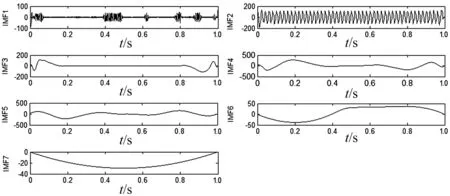
图7 EMD分解

为了具体对比递归VMD谐波检测效果，分别以原信号中的基波分量和谐波分量作为参考，计算EMD算法所提取的基波分量和谐波分量与原信号的基波分量和谐波分量的相关度。直接调用MATLAB中相关度计算命令R=corrcoef()，计算结果为：

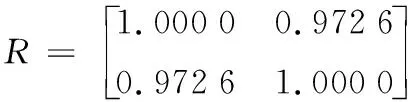
4 结束语

通过对比递归VMD与EMD分解结果的比较，递归VMD从基波分量的提取，以及各谐波分量的重构上都优于EMD方法。将递归VMD方法用于有源滤波器谐波检测，对原始电流或电压信号没有要求，且能将电力系统谐波自适应地分离出来。递归VMD通过改进FFT提高了VMD的运行速度，满足实时性。仿真结果表明，基于递归VMD的检测法可以实时、有效和准确地检测出电网中谐波分量。