一种用于风电并网的变阻尼无源控制方法

付永良， 陈新华

(国网德州供电公司，山东 德州 253000)

0 引 言

基于VSC-HVDC的风电并网系统是一个典型的高阶、多变量和强耦合的非线性系统，为实现系统的解耦控制，提高系统的暂态能力，需多种控制策略相结合。

目前，各种新型控制理论被应用于VSC-HVDC系统。文献[1]将模型预测的控制理论应用于VSC-HVDC系统中，达到了无源系统供电的目标。文献[2]利用欧拉-拉格朗日的数学模型并根据无源控制策略注入恒定阻尼的方式实现系统的稳定控制。文献[3]将整流侧和逆变侧变流器作为系统统一考虑，提出了一种基于无源性理论的联合控制方法。文献[4]通过一系列的矩阵构造能量函数，提出一种无源控制器。为减小直流侧电阻的扰动，为系统注入阻尼,但采用注入恒定阻尼的方法将降低控制系统对参数变化的灵敏度，从而降低系统的暂态性能。

本文利用变阻尼无源性控制理论，并根据耗散哈密顿系统的耗散原理，将两端的变流器系统看作是二端口的能量变换装置，将风电并网系统建成基于PCHD的数学模型。利用互联和阻尼配置的无源性控制方法，给出了风电并网系统的反馈镇定，并计算出可控制电压、功率大小的数学表达式。同时，为降低系统参数变化对控制系统带来的影响，向系统注入随参数变化而变的阻尼。在仿真系统中搭建的模型证明了本方法的有效性。

1 无源控制及VSC-HVDC的PCHD模型

端口受控哈密顿系统(PCH)是带有无源性和耗散性的[5]。系统方程:

(1)

式中：x∈Rn;u∈Rm;R(x)为半正定对称矩阵，体现端口附加阻尼；J(x)=-J(x)；H(x)为系统的能量函数；g(x)u可理解为外部输入。

为使系统稳定在期望的平衡点x*，可加入控制函数，得到系统期望的能量函数：

Hd(x)=H(x)+Ha(x)

(2)

寻找一个反馈控制u=α(x)，并调整互联和阻尼矩阵，使其闭环系统为：

(3)

式中：Jd(x)、Rd(x)分别为期望的互联矩阵、阻尼矩阵;Ha(x)为待定的哈密顿函数，表示通过控制注入到系统的能量;Hd(x)在期望的平衡点x*处取最小值[6]，那么x*就是闭环系统的一个稳定平衡点。

如果找到函数α(x)，Ja(x)，Ra(x)以及矢量函数K(x)满足：

(4)

并满足如下的条件[7]：

(1)保持结构性

Jd(x)=Ja(x)+J(x)=-[Ja(x)+J(x)]T

(5)

Rd(x)=Ra(x)+R(x)=[Ra(x)+R(x)]T

(6)

(2)可积性

(7)

(3)平衡点指定

(8)

(4)Lyapunov稳定性：在期望平衡点x*处，K(x)的雅可比式应满足边界条件：

(9)

则系统(1)为端口受控耗散哈密顿系统，在x*处，系统(1)是稳定的,反馈控制器则可由式(4)求出[7]。

应用于风电并网的VSC-HVDC系统整体结构如图1所示，电网侧、风电场侧换流器均采用电压源型，且拓扑结构相同。

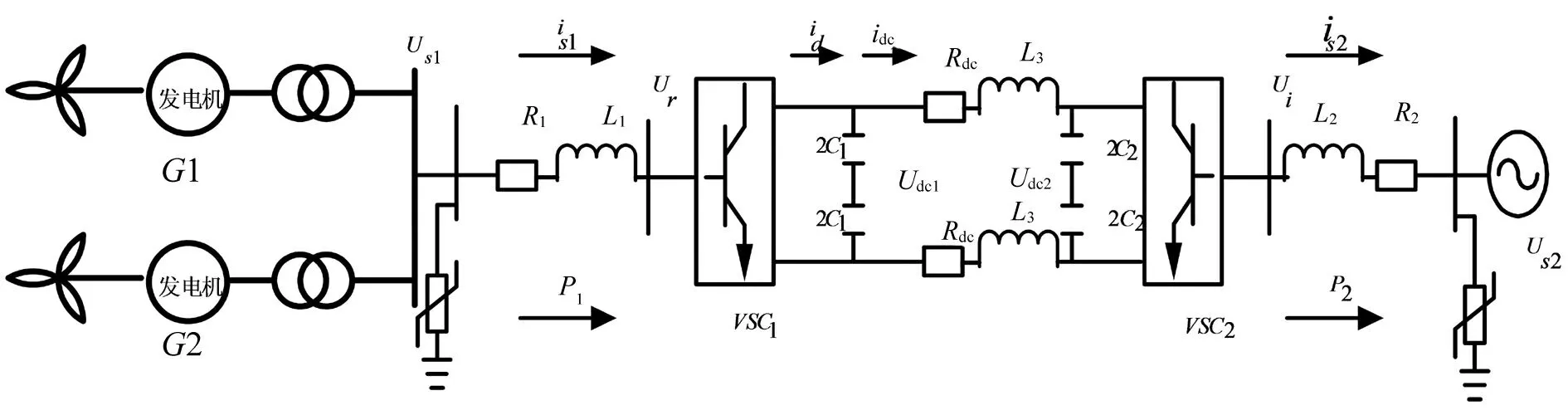
图1 用于风电并网的VSC-HVDC系统

图1中:Us1为风电场输出电压;Ur、is1分别为连接风电场侧变流器的交流电压和电流；Us2为电网电压;Ui、is2分别为连接电网侧变流器的交流电压和电流；R1、R2和L1、L2分别为两侧变流器的等效电阻、电感。dq坐标下风电场侧和电网侧的变流器模型[8]分别如下所示：

(10)

(11)

取风电场侧电压矢量的方向为旋转坐标的d轴分量方向，即Usd1=US1，Usq1=0，进而有：

(12)

将式(10)和式(12)联立，得风电场侧数学模型：

(13)

取状态变量：

x=[x1x2]T=[LP1LQ1]T=D[P1Q1]T

则风电场侧变流器的PCHD模型形式为：

(14)

对式(11)取状态变量：

x=[x1x2]T=[LisdLisq]T=D[isdisq]T

则电网侧变流器的PCHD模型形式为：

(15)

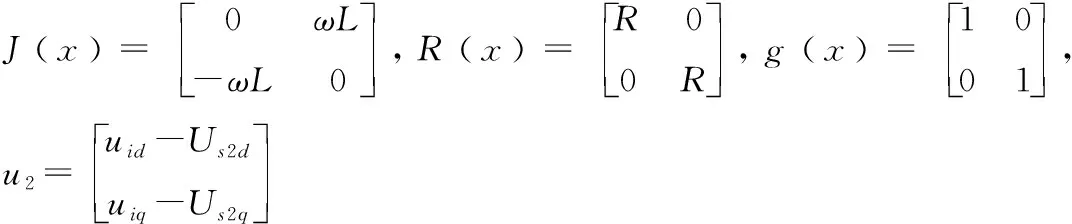
2 控制器设计

风电场侧变流站采用有功功率P1ref和无功功率Q1ref恒定的控制方式。

设系统(14)的能量函数为：

(16)

取系统(14)的状态误差为：

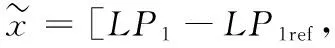
(17)

定义误差系统的哈密顿函数：

(18)

式中：Ja、ra1、ra2为待定的互联与阻尼参数。

由式(4)和式(18)可计算出风电场侧无源控制器的数学表达式：

(19)

在平衡点x*处，有：

(20)

(21)

借助La Salle不变集原理，可证明系统在x*处是渐近稳定的。

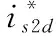
同样，取系统(15)的状态误差为：

(22)

定义误差系统的哈密顿函数：

(23)

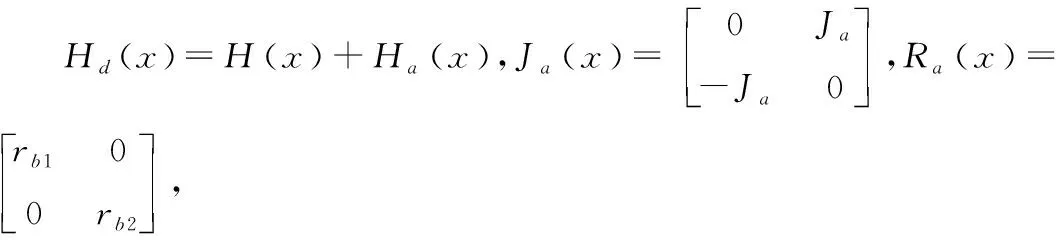
同理，可得电网侧变流器的控制率：

在平衡点x=x*处，有：

(25)

(26)

借助La Salle不变集原理，可证明系统在x*处是渐近稳定的。

3 变阻尼控制

对于两侧变流器的控制来讲，注入阻尼的取值直接影响所得控制器的性能：当注入阻尼过小，控制器达到稳态的时间会过长，且达到稳态的误差不理想；当注入阻尼过大时，无源控制器达到稳态的时间将减少，稳态性能变好，但系统电流电压畸变率过大。为此，本文提出在系统达到稳态前注入较大阻尼，提高系统的反应时间,稳态时，减小注入的阻尼，提高稳态精度。整个基于PCHD模型的变阻尼控制框图如图2所示。

由式(19)和式(24)可知，控制器的注入阻尼大小与ra1、ra2和、rb1、rb2大小有关。通常取ra1=ra2，rb1=rb2，因此，注入阻尼的大小仅与ra1，rb1有关。下面就以风电场侧变流器的阻尼注入为例，实现变阻尼的控制。针对阻尼变化的规律，本文采取二阶跟踪微分器来实现阻尼的可变注入。

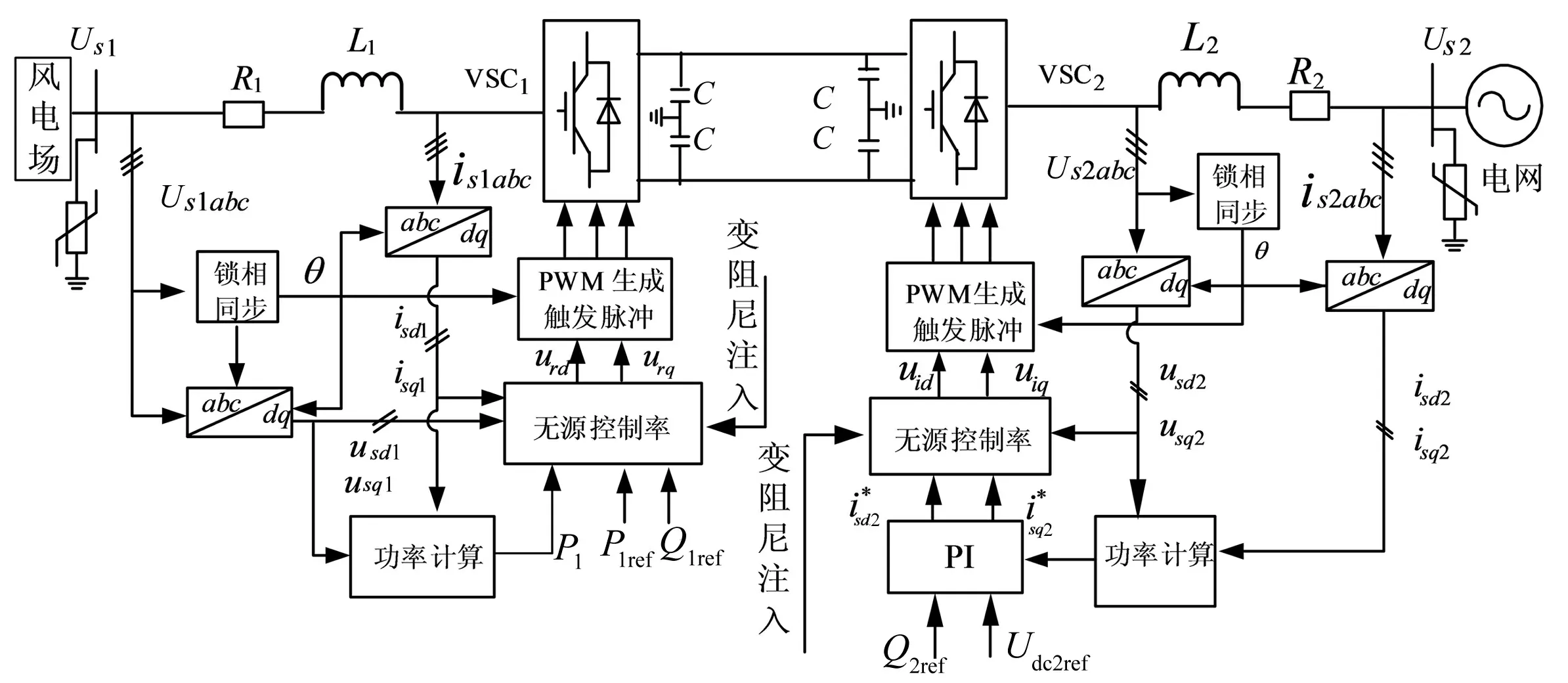
图2 基于PCHD模型的风电并网系统的变阻尼控制框图

二阶跟踪微分器可以描述成如下的系统：输入一个信号ν(t)，系统将输出两个信号y1，y2,其中y1跟踪输入信号ν(t)，而y2可看作是ν(t)的近似微分。二阶微分跟踪器的非线性函数如图3所示。

二阶跟踪微分器的数学方程式如下：

(27)

其中表达式：

(28)

且δ≥0。

本文所研究的变阻尼控制需要启动时注入大的阻尼，稳态时注入小的阻尼，所以本文将上述的输出反用，可得下式：

(29)

其中表达式：

(30)

式中：δ≥0;k1为初始时刻期望阻尼;k2为稳态时期望阻尼;y为阻尼的实时注入值。

4 分析验证

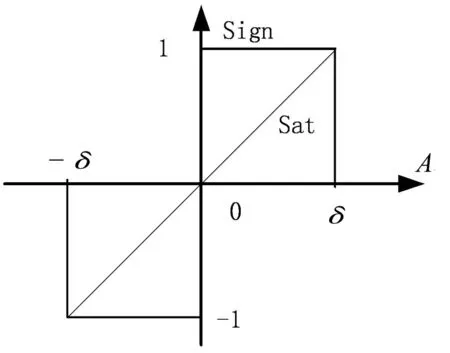
图3 二阶微分跟踪器的非线性函数

为验证本文设计的变阻尼无源控制方法的有效性，在MATLAB/Simulink中进行了建模和仿真。其系统的主要电气量参数如表1所示。

其中控制器参数δ选取0.08，a取1 500，k1取200，k2取90。

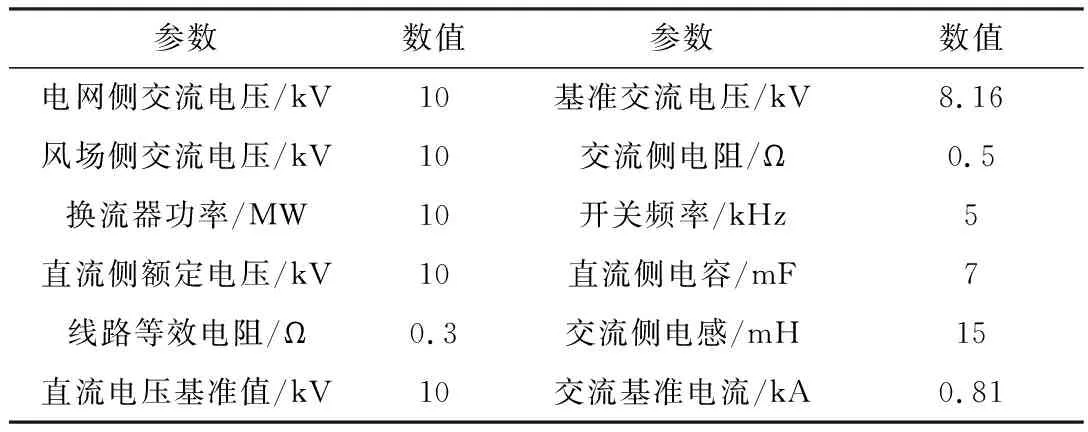
表1 仿真参数

根据直流输电控制方法，风电场侧换流器将采用有功功率、无功功率固定的控制。为避免直流系统电压振荡，电网侧换流器直接将直流电压和无功功率固定在期望值。

设风电场侧有功功率为1 pu，无功功率为0。电网侧无功功率为0，直流电压为1 pu。风电场侧各电气量仿真波形如图4所示。

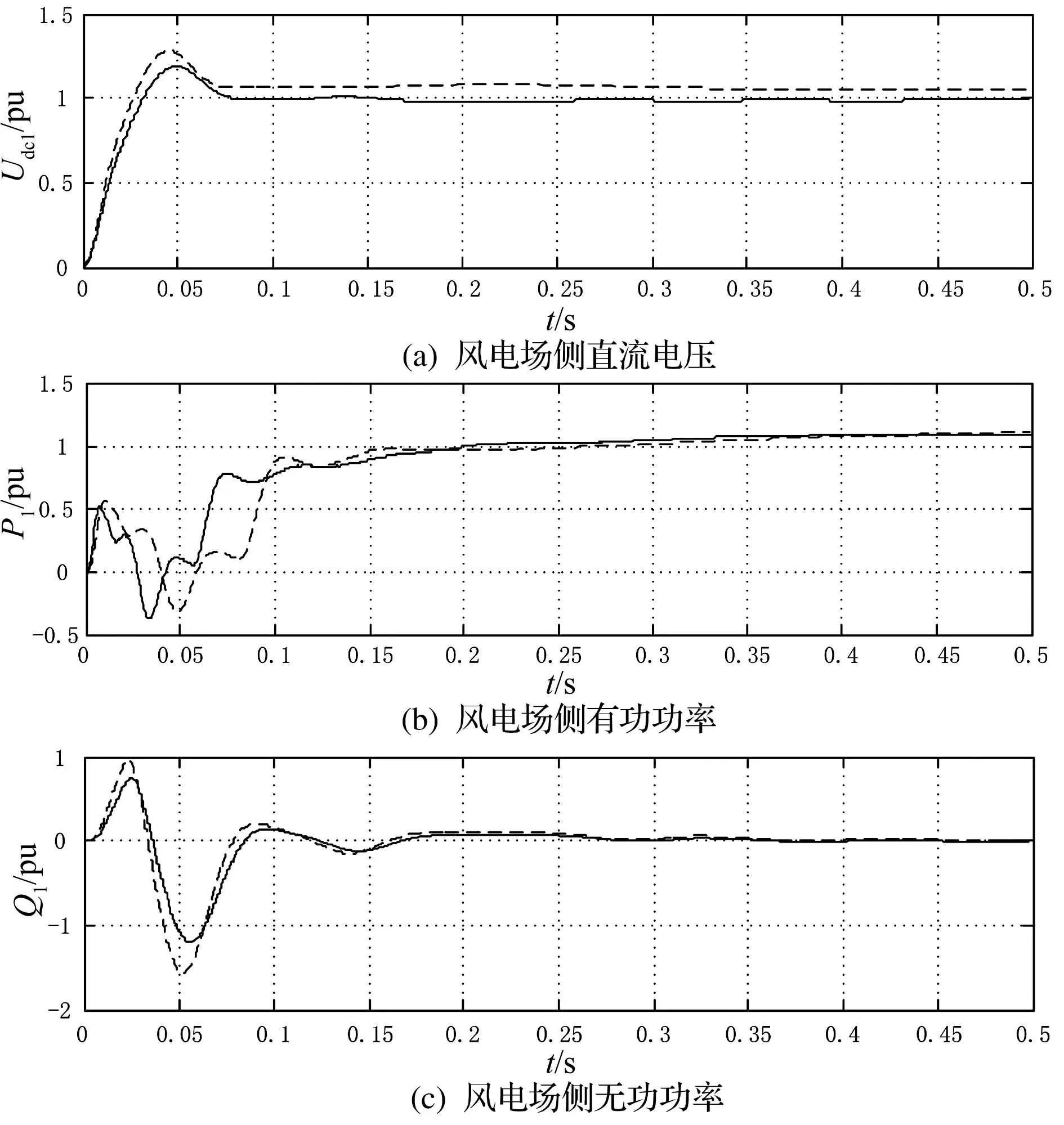
图4 风电场侧的波形

电网侧各电气量仿真波形如图5所示。

图4、图5中，虚线为恒定阻尼控制的动态响应波形，实线为本文设计的变阻尼无源控制的动态响应曲线。对比两种控制方式的结果，可知变阻尼无源控制不仅能够实现对变流器的控制，而且其响应时间更短，达到稳态的精度也更高。

5 结束语

本文建立了应用于风电并网的直流输电系统的数学模型，并在此基础之上，提出了一种无源控制策略，为进一步提高控制器的稳态精度、响应速度采用了二阶跟踪微分器向系统注入可变阻尼。与恒定阻尼控制方法对比，本文设计的变阻尼无源控制器的响应速度更快，稳态时的精度更高，为直流输电系统的控制提供了一种新方法。

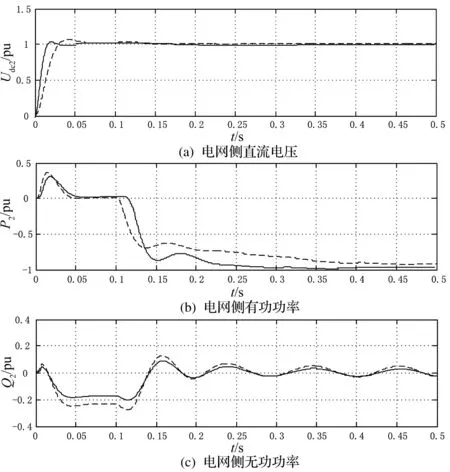
图5 电网侧的波形